VL 16
Werbung

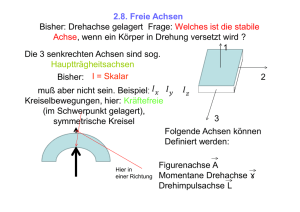
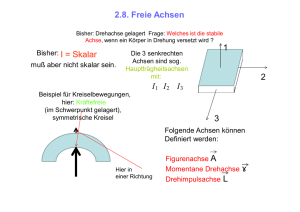
Mechanik II / Vorlesung 16 / Prof. Popov I. Drehimpuls bei einer Drehung um eine beliebige Achse G ω x = ω cosα ω ω y = ω sin α a y G G mb2 L F Θx = 12 b G ma 2 α Θ = −F y β 12 x b tan α = . a 2 mb ω cosα Lx = Θ xω x = 12 ma 2 ω sin α Ly = Θ yω y = 12 a 2 sin α a 2 b a = 2 = = tan −1 α . tan β = 2 b cosα b a b Der Vektor des Drehimpulses dreht sich um die Achse. Das heißt, er ändert sich. II. Zeitliche Änderung eines rotierenden Vektors. G Wenn ein Vektor A sich mit der WinkelgeG schwindigkeit ω dreht, so gilt G G G A =ω × A. Beispiele: G G G G (a) Geschwindigkeit v = r = ω × r (b) Beschleunigung G G G G G G G a = v = ω × v = ω × (ω × r ) (c) Änderung des Drehimpulses G G G L =ω ×L III. Die in der Achse bei einer Rotation wirkenden Kräfte. Nach dem Drehimpulssatz G G G G L =ω ×L = M . Ändert sich der Drehimpuls, so muss ein Kraftmoment wirken! Die Änderung des Drehimpuls zeigt in die Tafel. In den Lagern muss somit ein Kräftepaar wirken, wie im Bild 1 gezeigt. Woher stammt dieses Kraftmoment? Betrachten wir die Platte im rotierenden Bezugssystem. Durch die Zentrifugalkräfte entsteht ein Kraftmoment in der gezeig- Kreiselbewegung ten Richtung. Die Reaktionskräfte in den Lagern wirken in die entgegensetzte Richtung. Was geschieht, wenn die Achse nicht festgehalten wird? IV. Symmetrischer Kreisel Definition: Θ x = Θ y ≠ Θ z . Zum Beispiel: A. Reguläre Präzession (Nutation) eines symmetrischen Kreisels. G G L1 = Θ1ω1 ω L L2 = Θ2ω 2 = 0 x3 L3 = Θ3ω3 Winkelgeschwindigkeit der Drehung um die x1 Symmetrieachse: θ L L cosθ ω3 = 3 = Θ3 Θ3 L sin θ ω1 = ω Pr sin θ = . Θ1 L Daraus ω Pr = . Die Kreisachse beschreibt Θ1 G einen Kreiskegel um die Richtung L . V. Präzession unter der Einwirkung eines Kraftmomentes G Wenn wir ω die G -F L in die Kreiselachse Tafel gerich- gleichmäßig tet G um die F Ω vertikale Achse drehen, wie ändert sich der Drehimpuls? G G G G L =ω ×L = M Wenn die Kräfte in vertikaler Ebene wirken, so bewegt sich die Achse in der horizontalen Ebene VI. Spielkreisel G L Ω Pr G ω θ h mg 1 L = Ω Pr L sinθ = mgl sinθ ⇒ Ω Pr = mgl mgl = L Θω Astronomisches Beispiel: Präzession der Erde Sonne Periode der 25800 Jahre. astronomischen Präzession VII. Präzession und Nutation G Ω Pr äz G ω Nut VIII. Satz vom gleichsinnigen Parallelismus der Drehachsen (Foucault) Die Kreiselachse versucht sich gleichsinnig parallel mit der Achse der Zwangsdrehung zu stellen. 2