E1 V9 überarbeitet_JR

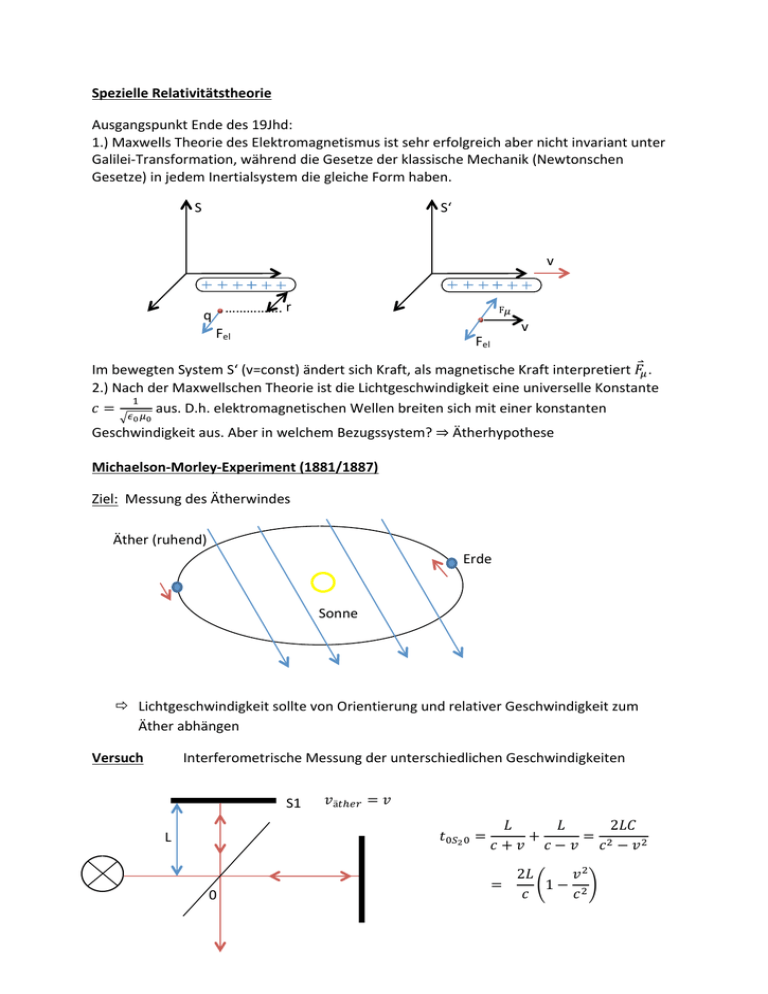
Spezielle Relativitätstheorie Ausgangspunkt Ende des 19Jhd: 1.) Maxwells Theorie des Elektromagnetismus ist sehr erfolgreich aber nicht invariant unter Galilei-­‐Transformation, während die Gesetze der klassische Mechanik (Newtonschen Gesetze) in jedem Inertialsystem die gleiche Form haben. S S‘ v ……………. r F! q v Fel Fel Im bewegten System S‘ (v=const) ändert sich Kraft, als magnetische Kraft interpretiert 𝐹! . 2.) Nach der Maxwellschen Theorie ist die Lichtgeschwindigkeit eine universelle Konstante !
𝑐 = ! ! aus. D.h. elektromagnetischen Wellen breiten sich mit einer konstanten ! !
Geschwindigkeit aus. Aber in welchem Bezugssystem? ⇒ Ätherhypothese Michaelson-­‐Morley-­‐Experiment (1881/1887) Ziel: Messung des Ätherwindes Äther (ruhend) Erde Sonne ð Lichtgeschwindigkeit sollte von Orientierung und relativer Geschwindigkeit zum Äther abhängen Versuch Interferometrische Messung der unterschiedlichen Geschwindigkeiten S1 𝑣ä!!!" = 𝑣 𝑡!!! ! =
L 0 𝐿
𝐿
2𝐿𝐶
+
= !
𝑐 + 𝑣 𝑐 − 𝑣 𝑐 − 𝑣!
2𝐿
𝑣!
= !1 − ! ! 𝑐
𝑐
Seite | 48 L S2 !
𝑐²𝑡!"
!
= 𝐿² +
Det !!
→ 𝑡!"! ! = ! !
𝑣²𝑡!"
!
! !!
!
!
≃ !
!! !
!
!!
!
!!
1 + ! ! !! ! !
→ Δ𝑡 = ! ! ! Bei Drehung um 90° erwartet man → Δ𝑡 = ! ! ! Zu erwartender Effekt: Verschiebung in Einheiten der Wellenzahlverschiebung Δ𝑁 !
𝑇 = ! , 𝑓 ∗ 𝜆 = 𝑐 (𝑓: Frequenz, 𝜆: Wellenlänge) Δ𝑁 = 𝑓 ∗ Δ𝑡 =
!! ! !
! !!
𝐿 = 1𝑚 𝜆 = 5,46 ∗ 10!! 𝑚 [grüne Kf Linie] 𝑣 = 30
!
Erde um Sonne) 𝑐 = 3 ∗ 10! ! → 3,6 ∗ 10!! Streifenabstände (schwer zu messen) Ergebnis der Messung (M.M. 1887): !"
!
!
= 3 ∗ 10! ! (Bahngeschwindigkeit Δ𝑁 ≤ 0,01 → negativ Heute (2009) mit Resonatoren 𝑐 − 𝐴𝑛𝑖𝑠𝑜𝑡𝑟𝑜𝑝𝑖𝑒 ≤ 10!!" ⇒ keine Verschiebung Mögliche Konsequenzen/Erklärungen I !!
Länge in Bewegungsrichtung zum Äther um Faktor 1 − ! ! verkürzt. II Äther wird mitgeführt III kein Äther, Lichtgeschwindigkeit konstant relativ zur Lichtquelle IV Lichtgeschwindigkeit unabhängig von Bewegung des Beobachters, kein Äther Unabhängig von der Bewegung des Beobachters misst er dieselbe Geschwindigkeit: !
!
𝑐 = 299792458 ! ≈ 3 ∗ 10! ! Ad (I) unnatürliche Ad-­‐hoc-­‐ Erklärung ad(II) Fizeau-­‐Experiment (1851) H2O Messung von c in strömenden Medien Seite | 49 ð c ist v-­‐abhängig, aber auch vom Medium (bestätigt Fresnels Theorie) ð weitere ad-­‐hoc-­‐Annahmen über den Äther nötig Ad(III) Experiment von Sadeh (1963) Folie 𝛾 Det
𝛾 !
𝑒 , 𝑣 ≃ 𝑐 !
𝛽 − 𝑆𝑡𝑟𝑎ℎ𝑙𝑒𝑟 Koinzidenz Det
𝛽 ! Strahlen (Positronen) treffen auf Folie (viele 𝑒 ! ) 𝑒 ! + 𝑒 → 2𝛾 Paarvernichtung !
→ 𝛾 −Quelle, die sich mit ~ ! nach rechts (oben) bewegt! !
!
(𝑣! + 𝑣! ! ) ∗ ≈ (𝑐 + 0) ∗ !
!
→ trotzdem kommen 𝛾 gleichzeitig an Konsequenz: èkein Äther, c konstant und unabhängig von Bewegung des Beobachters Einsteinsche Postulate: (I)
Naturgesetze sind in allen Inertialsystemen gleich. (Relativitätsprinzip) (II)
Lichtgeschwindigkeit ist in allen Inertialsystemen gleich. Aus I + II Ableitung der Lorentztransformation für die Mechanik. Einstein Annalen der Physik 17 891 (1905) Die Lorenztransformation Wie müssen Koordinaten transformiert werden, so dass beide Einstein’schen Postulate (c = const. & Rel. Prinzip) erfüllt sind? Lichtblitz bei 𝑡 = 𝑡 ! = 0 Im Ursprung (0,0! ) S‘ S v Lichtblitz 0 Es gilt (𝐴) 𝑖𝑛 𝑆 𝑥 = 𝑐𝑡 wegen I und II 𝑐 = 𝑐𝑜𝑛𝑠𝑡 𝑡 ! = 𝐸𝑖𝑔𝑒𝑛𝑧𝑒𝑖𝑡 𝑖𝑛 𝑆′ 𝑥 ! = 𝑐𝑡 ! !
⬚
0‘ x Seite | 50 Ansatz: „korrigierte“ Galileitransformation 𝐵 !
𝑥 ! = 𝑥 − 𝑣 ∗ 𝑡 !"##$!%&# 𝑥 = 𝑦(𝑥 − 𝑣𝑡)
Klassisch: 𝑥 = 𝑦(𝑥 ! + 𝑣𝑡 ! )
𝑥 = 𝑥 ! + 𝑣 ∗ 𝑡′
!
Wir führen Korrektur 𝛾 ein, so dass 𝐴 und 𝐵 erfüllt wird. 𝑐 𝑡 ! = 𝛾 𝑐 − 𝑣 𝑡 𝑥 𝑐𝑡 = 𝛾 𝑐 + 𝑣 𝑡′ 𝑐 ! 𝑡𝑡 ! = 𝛾 ! 𝑐 ! − 𝑣 ! 𝑡𝑡 ! 𝛾 ! =
!!
!!! !!!
→ 𝑦 =
!
!!
!! !
!
Lorentz Faktor 𝛾 Def.: relativ Geschwindigkeit: !
𝛽 = ! 1,15 1 𝛾=
0,5 ! !
!
!
𝑡! = !
= 𝛾 𝑡 − ! 1 − !!
!
− 𝑥! = !
!
!!!! !
𝛽 1 Transformation der Zeit: !
!
!
− 𝑦 𝑥 − 𝑣𝑡
!"
= 𝛾 𝑡 − ! ! Zusammen: Lorentztransformationen: 𝑥! =
!!!"
!
! !!!!
!
!"
!! !
!
𝑡 = ! ! !!!!!
!
Grenzfall 𝑦! = 𝑦
𝑧! = 𝑧
𝑣 ≪ 𝑐 𝛾 𝑣 ≈ 1 Seite | 51 Galilei Transformation 𝑥′ = 𝑥 − 𝑣𝑡 𝑡 ! = 𝑡 Konsequenz der Lorentztransformation: → Zeit und Raum sind nicht mehr unabhängig Spezielle Relativitätstheorie ist erste große „Vereinigungstheorie“ -­‐
-­‐
-­‐
Raummetrik, Zeitmetrik Massenerhaltung, Energieerhaltung El. Feld, mgn. Feld Raumzeitmetrik Energie-­‐ Masse. Erhaltung el. magn. Feld → → → Zeitdilatation 𝑡! =
𝑣
∗𝑥
𝑐!
𝑣!
1− !
𝑐
𝑡−
Einsteins „Lichtuhr“ Lichtpuls läuft rauf und runter Spiegel L L 2 Lichtpuls Spiegel 𝑣∗
!!
Δ𝑡 ! = ! Im ruhenden System → ruhende Uhr !!
!
im bewegten System → mit 𝑣 ≠ 0 bewegte Uhr 𝑐∗
!!
!
𝐿! + 𝑣 ∗
=
!! !
!
!
!
!
!
𝑐 Δ𝑡 = 2𝐿 + 𝑣Δ𝑡 Δ𝑡 = Δ𝑡 ! ∗ 𝛾 Δ𝑡 =
!!
!
∗
!
!!
!! !
!
= Δ𝑡 ! 𝛾 Δ𝑡′ Δ𝑡 = Δ𝑡 ! 𝛾 Zeitdilatation „bewegte Uhren gehen langsamer“ Experimentelle Beispiele: Zerfall von Myonen „schweres Elektron“ !!!,!"!"
𝜇
𝑒 ! + 𝑣! + 𝑣! + Energie 𝑚! ≈ 200 𝑚! Seite | 52 Im CERN: Myonenspeicherung mit 𝑣! = 0,9994 ∗ 𝑐 𝜏
1,52𝜇𝑠
𝜏! =
=
= 44,6𝜇𝑠 𝑣!
1 − 0,9942!
1− !
𝑐
Halbwertszeit um Faktor 29,4 verlängert. „Rasche Bewegung wirkt lebensverlängernd“ Atomuhren im Flugzeug (Maryland-­‐Experiment, 1975) Flughöhe ℎ = 10 𝑘𝑚 !!
!!
𝑡 = 𝑡! ∗ 1 − ! ! ≃ 𝑡! 1 − !! ! Flugdauer Δ𝑡 = 15 ℎ !"
Fluggeschw. 𝑣 = 500 ! Δ𝑡 𝑔 Exp 0 𝑣 𝑡 Maryland: Gravitationseffekt überwiegt → Uhren gehen schneller. Längenkontraktion Geschwindigkeitseffekt Δ𝑡! = 𝑡 − 𝑡! !!
≃ − !! ! 𝑡! Gravitationseffekt (ART) !!
Δ𝑡! = + ! ! 𝑡! Was passiert mit Längenmessungen in unterschiedlichen Inertialsystemen? Betrachte Lichtuhr, die „auf der Seite liegt“ 1. Ruhesystem der Uhr S‘ Lichtpuls Δ𝑡 ! =
!!!
!
2. Relativ dazu bewegtes System S 1 3 1 2 2 3 Spiegelpositionen 1, 2, 3 L 𝑐𝑡!" = 𝐿 + 𝑣𝑡!" → 𝑡!" =
𝐿
𝑐−𝑣
Seite | 53 𝐿
𝑐+𝑣
2𝑐𝐿
2𝐿
→ Δ𝑡 = 𝑡!" + 𝑡!" = !
=
∗ 𝛾 ! (∗) !
𝑐 −𝑣
𝑐
Andererseits gilt Zeitdilatation Δ𝑡 = Δ𝑡 ! 𝛾 2𝐿!
→ Δ𝑡 =
𝛾 𝑐
𝑐𝑡!" = 𝐿 − 𝑣𝑡!" → 𝑡!" =
!"#(∗)
𝐿 =
𝐿!
𝑣!
= 𝐿′ 1 − ! 𝛾
𝑐
Längenkontraktion bewegte Maßstäbe erscheinen verkürzt 𝐿!"!!
𝐿=
𝛾
Zeitdilatation und Längenkontraktion folgen auch direkt aus der Lorentztransformation -­‐
-­‐
System der ruhenden Uhr S‘ Relativ dazu bewegtes System S Lorentztransformation → 𝑡! − 𝑡! =
𝑡!!
−
𝑡!!
! !!! !!!!
+
!²
!!
!! !
!
Uhr ruht in 𝑆 ! → 𝑥!! = 𝑥!! → Δ𝑡 = Δ𝑡 ! ∗ 𝛾 -­‐
-­‐
System des ruhenden Maßstabs S‘ Relativ dazu bewegtes System S → 𝑥!! − 𝑥!! =
𝑥! − 𝑥! − 𝑣 𝑡! − 𝑡!
𝑣!
1− !
𝑐
Längenmessung in S bedeutet, dass man Anfang und Ende des Maßstabs gleichzeitig bestimmt → 𝑡! − 𝑡! = 0 → 𝐿!"!! = 𝐿 ∗ 𝛾 oder 𝐿 =
!!"!!
!
Seite | 54 Geschwindigkeitsaddition: 𝑣! + 𝑣!
𝑣=
𝑣 𝑣 1 + !!!
𝑐
Teste Symmetrien und Grenzfall 𝑣 ≪ 𝑐 ! !
γ=
!!
Lorentzfaktor !! !
!
Taylorentwicklung Annäherung der Funktion 𝑓(𝑥) im Punkt 𝑥! durch Potenzen 𝑥 ! − 𝑥! ! 𝑥 𝑥! 1
𝑓 𝑥 = 𝑓 𝑥! + 𝑓 ! 𝑥! ∗ 𝑥 − 𝑥! + 𝑓 !! 𝑥! 𝑥 − 𝑥!
2
1 !
… + 𝑓
𝑥! 𝑥 − 𝑥! ! + 𝑅!!! (𝑥) 𝑛!
Beispiel Entwicklung um 𝑣 = 0 !
𝛾 𝑣 =
𝛾 ! 𝑣 = 0 = 0 !
!
+ !
!! !
!
!!
!
≈ 1 ∗ ! ∗ ! ! + ⋯ 1
𝑣
− −2 !
2
𝑐
𝛾! 𝑣 =
! 𝑣! !
1− !
𝑐
1
𝛾 = !
𝑐
!!
1
𝑣!
1− !
𝑐
!
!
−
!
𝛾 !! 𝑣 = 0 = ! ! 𝑣∗ −
3
2
−2 ∗
𝑣!
1− !
𝑐
!
!
𝑣
𝑐 ! Experimentelle Befunde: Zeitdilatation und Längenkontraktion 𝑇! = 1,52𝜇𝑠 !
-­‐
-­‐
Zerfall von Myonen 𝜇 → 𝑒 ! + 𝑣! + 𝑣! + 𝐸𝑛𝑒𝑟𝑔𝑖𝑒 „schweres Elektron“ 𝑚! ≃ 200𝑚! 𝑇! Halbwertszeit !
-­‐
Myonen entstehen durch kosmische Strahlung in der oberen Atmosphäre und bewegen sich nahezu mit c Klassisch: nach 𝑐 ∗ 𝑇! ≃ 450𝑚 ist die Hälfte der Myonen zerfallen !
Seite | 55 Gleichzeitigkeit Vergangenheit – Gegenwart – Zukunft Kann sich im relativistischen Systemen ändern bzw. umkehren. v A‘ K‘ B‘ A‘ K‘ c c B‘ A A B B K K K sieht beide Blitze gleichzeitig K weiß: K‘ bewegt sich, also sieht K‘ zuerst B-­‐Blitz dann A-­‐Blitz K‘ ist in einem Inertialsystem (mit c=const), Da A‘ und B‘ gleiche Entfernung, kommt K zu dem Schluss, dass B-­‐Blitz vor A-­‐Blitz eingeht. Für jeden Beobachter ist die Gleichzeitigkeit zweier Ereignisse an verschiedenen Raumpunkten abhängig von verwendetem Bezugssystem! Wann erreichen die Blitze das vordere bzw. hintere Wagenende? Im Wagen (S‘) c=const, beide Enden gleich weit weg → Lichtblitze erreichen Enden gleichzeitig Auf dem Bahnsteig (S) c=const. § Hinteres Ende bewegt sich auf Ort des Blitzes zu, vorderes vom Ort des Blitzes weg → Lichtblitz erreicht hinteres Ende vor dem vorderen Ende! Für jeden Beobachter ist die Gleichzeitigkeit zweier Ereignisse an verschiedenen Raumpunkten abhängig vom verwendeten Bezugssystem! Minkowski – Diagramm Raum-­‐Zeit Diagramm: „Ereignisraum“ ct 𝑥 = −𝑐𝑡 Lichtblitz nach links tb t’a=t‘b A 0 𝑥 = 𝑐𝑡 Lichtblitz nach rechts x‘ E ta ct‘ 𝑣
𝛼, tan 𝛼 = 𝑐
B Weltlinien der Wagenenden A,B x Seite | 56 -­‐
Lorentztransformation 𝑥! , 𝑡! → 𝑥!! , 𝑡!! der Koordinaten eines Ereignisses 𝐸 𝑠 ! = 𝑐𝑡 ! − 𝑥 ! = 𝑐𝑡 ! ! − 𝑥 ! ! ⇒ unverändert bei Lorentz-­‐Transformation! Zukunft Δ𝑠 ! < 0 𝐸! 𝐸! 𝐸! Δ𝑠 ! > 0 x Vergangenheit In 𝑆 𝑡! < 𝑡! ! In 𝑆 ! 𝑡!! = 𝑡! ′ → 1) x‘-­‐Achse parallel zur Verbindungslinie der Ankunftsereignisse (Licht am Wagenende) 2) Abstand von A, B zeitlich konstant, Wagenenden ruhen in S‘ → t‘ Achse parallel zu Weltlinien von A,B !
!
→ Minkowski – Diagramm entspricht Lorentztransformation 𝑥!,! , 𝑡!,! → 𝑥!,!
, 𝑡!,!
Hier z.B. Längenkontraktion und Zeitdilatation offensichtlich c = const. erfüllt, da Lichtgerade Winkelhalbierende der Achsen Kausalität und c als Grenze Betrachte Ereignisse A und B zwischen denen man nur mit Überleichtgeschwindigkeit reisen kann. Also 𝑥! − 𝑥! > 𝑐 ∗ 𝑡! − 𝑡! ct ct‘ Lichtgerade In S ist A vor B x‘ A B In S‘ ist B vor A x → A,B können nicht kausal miteinander verknüpft sein → Informationsaustausch mit Überlichtgeschwindigkeit nicht möglich 𝑠² = 𝑥² − 𝑐𝑡 ! = 𝑥 ! ! − 𝑐𝑡 ! ! ist konstant unter Lorentztransformation Klassifiziere Ereignisse nach ihrem raumzeitlichen Abstand Δ𝑆² Seite | 57