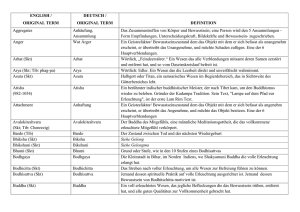
Michelson - Interferometer

Michelson - Interferometer
Matthias Lütgens
9. April 2005
Partner: Christoph Mahnke
Betreuer: Dr. Enenkel
Datum der Versuchsdurchführung: 5. April 2005
0.1
Ziel
Experimentelle Nutzung des Michelson-Interferometers als Gerät der modernen Präzisionsmesstechnik zur
Messung von Längen im nm-Bereich.
0.2
Aufgaben
1. An dem gegebenen Michelson-Interferometer ist der Mikrometerbetrieb der verstellbaren Spiegels mit
dem Licht eines He-Ne-Lasers (λ
= 632, 8 nm)
zu kalibrieren.
2. Die Kohärenzlängen des Lichtes gegebener Lichtquellen (Hg-Höchstdrucklampe, Glühlampe) sind zu
messen.
3. Die Schwebung der beiden Na-D-Linien ist zu beobachten. Aus der Schwebungswellenlänge ist die
Wellenlängendierenz
∆λ der Na-Linien experimentell zu ermitteln, wobei eine der beiden Wellenlängen
als bekannt vorausgesetzt wird.
4. Die Dicke eines gegebenen Mikroskopdeckgläschens ist unter Verwendung von Licht mit kleiner Kohärenzlänge zu bestimmen.
1
1
Vorbetrachtung
Abbildung 1: schematischer Aufbau eines Michelson-Interferometers
1.1
Interferenz von Licht
Treen zwei Wellen gleicher Frequenz aufeinander, so überlagern sich ihre Auslenkungen (Elongationen). Die
resultierende Intensität der entstehenden Welle hängt vom Gangunterschied
∆s
der beiden Teilwellen ab.
Für
∆s = k · λ (k ∈ Z)
ergibt sich maximale Verstärkung (konstruktive Interferenz), für
∆s =
2k + 1
· λ (k ∈ Z)
2
maximale Abschwächung (destruktive Interferenz). Bei gleicher Amplitude löschen sich die Wellen bei destruktiver Interferenz vollständig aus.
1.2
Kohärenz von Licht
Zeitlich stabile Interferenzmuster sind nur zu beobachten, falls die Phasendierenz zwischen den Teilwellen
in jedem Raumpunkt zeitlich konstant ist. In diesem Fall nennt man die Wellen räumlich kohärent.
Ist die Phasendierenz in je zwei beliebigen Raumpunkten, die von einer Welle durchlaufen werden, zeitlich
konstant, so ist die Welle zeitlich kohärent. Eine räumlich und zeitlich kohärente Lichtquelle ist der Laser,
der praktisch kontinuierliche Lichtwellen aussendet. Deshalb kann unter Zuhilfenahme eines Lasers auch die
Kalibrierung des Mikrometerbetriebes vorgenommen werden. Natürliches Licht hingegen ist sowohl zeitlich
als auch räumlich inkohärent, denn das von den Atomen einer Lichtquelle ausgesandte Licht besteht aus
einzelnen Wellenzügen mit endlicher Länge (Kohärenzlänge) und ohne feste Phasenbeziehung untereinander.
1.3
Der Michelson-Interferometer
Variiert man den Wegunterschied
renzmuster. Nach einer Änderung
∆s bei der Interferenz zweier
∆s = λ ergibt sich wieder das
Teilstrahlen, so verändert sich das InterfeMuster, welches man ohne Wegunterschied
erhalten würde. Damit ist es prinzipiell möglich zum einen, durch Ändern von
2
∆s
um eine bekannte Strecke,
die Wellenlänge des verwendeten Lichtes aus der Anzahl der Helligkeitswechsel zu bestimmen, zum anderen ist es auch möglich, bei bekannter Wellenlänge, Änderungen des Lichtweges oder des Brechungsindizes
(ebenfalls eine Änderung des optischen Lichtweges) zu ermitteln.
Eine Anordnung, um solche Messungen durchzuführen, ist der Michelson-Interferometer (Aufbau siehe
Abbildung 1). Eine Lichtquelle strahlt Licht aus, welches durch das Aufweitungssystem, bestehend aus einer
Sammellinse, gelangt und auf einen Strahlteiler trit. Ein Teil des Lichtstrahls wird reektiert und trit
auf den beweglichen Spiegel 1. Der Rest des Strahls gelangt durch den Strahlteiler, und trit auf den festen
Spiegel 2. Die Lichtstrahlen werden jeweils vollständig reektiert und treen wieder auf den Strahlteiler. Dem
Experimentator interessiert nun zum einen der Anteil des Teilstrahls, welcher vom Spiegel 1 reektiert wurde,
der durch den Strahlteiler gelangt, und der Anteil des zweiten Teilstrahls, welcher vom Spiegel 2 reektiert
wurde, der nun auch am Strahlteiler reektiert wird. Haben diese beiden Teilstrahlen den Strahlteiler passiert,
so kann es zu Interferenzerscheinungen kommen, die dann auf dem Schirm sichtbar sind.
2
Versuchsdurchführung
Für die Bearbeitung der Aufgaben habe ich folgende Geräte benutzt:
•
Michelson - Interferometer
•
Schirm
•
Aufweitungssystem
•
Sensor mit Zähler
•
He-Ne-Laser
•
Hg - Höchstdrucklampe
•
Glühlampe
•
Na- Lampe
•
Mikroskopdeckgläschen
2.1
Justage des Interferometers und Kalibrierung des Mikrometerbetriebes
Zur Justage des Interferometers wird das Aufweitungssystem entfernt und der Verlauf des Strahles beobachtet, wobei als Lichtquelle ein He-Ne-Laser dient. Um die Strahlen teilweise ausblenden zu können, werden
Metallplättchen vor die Spiegel gestellt. Das Interferometer ist als justiert anzusehen, wenn die Lichtstrahlen
in einen Punkt auf den Schirm treen. Anschlieÿend wird das Aufweitungssystem wieder zwischen Laser
und Strahlteiler gebracht. Interferenzerscheinungen werden sichtbar in Form von konzentrischen Kreisen. Die
ebenen Wellen, die von dem Laser erzeugt werden, werden nach dem Passieren des Aufweitungssystems zu
Kugelwellen. Damit wird das paralelle Laserlicht zu divergentem Licht. Dreht man an der Feintriebschraube
des beweglichen Spiegels, fällt auf, dass bei annähernd gleichem Abstand der Spiegel zum Strahlteiler wenige, dafür aber breite Kreise zusehen sind, und bei groÿem Gangunterschied viele, schmale Kreise zu sehen
sind. Dieses liegt daran, dass bei groÿem Gangunterschied die Krümmungsradien der Wellenfronten stark
unterschiedlich sind, es also bei der Überlagerung häuger zu Maxima und Minima kommt. Anders verhält es
sich bei geringem Gangunterschied. Hier sind die Krümmungsradien ähnlich groÿ, und so kommt es zu nicht
sovielen Überschneidungen von Maxima und Minima, weshalb nur wenige aber breitere Kreise zu sehen
sind. Weiterhin ist zu sagen, dass bei nur minimalem Gangunterschied die Ringe nicht mehr ideale Kreise
sein müssen. Dies liegt an kleinen Fehlern an den Spiegeln, die erst hier zu sehen sind.
Um nun den Mikrometerbetrieb zu kalibrieren, verwenden wir einen Zähler, welcher Hell-Dunkelübergänge
zählt. Bei bekannter Wellenlänge (λ
= 632, 8 nm)
ist es somit möglich die Länge eines Skalenteils zu bestim-
men. Wir drehen die Feinmessschraube jeweils um 10 Skalenteile und lesen anschlieÿend die Helldunkelwechsel
3
ab. Zubeachten ist, dass die optische Wegänderung, die das Licht durchläuft, doppelt so lang ist wie der mechanische Weg. Somit ergibt sich die Länge eines Skalenteils aus:
k=
nλ
2 · 10
Die Messung wurde an verschiedenen Stellen des Mikrometerbetriebes durchgeführt, um systematische Fehler
durch Unregelmäÿigkeiten im Gewinde zu verringern.
Tabelle 1: Messung zur Kalibrierung
Nr.
Skalenteile in SkT
Anzahl der Hell-Dunkelwechsel n
1
10
311
2
10
320
3
10
318
4
10
314
5
10
314
6
10
316
7
10
313
8
10
315
9
10
321
10
10
317
11
10
320
12
10
318
13
10
321
14
10
318
15
10
316
16
10
316
n̄
Standardab. sn
Mittelwert
316,75
2,9326
Die Länge pro Skaleneinteilung ergibt sich dann zu:
k=
316, 75 · 632, 8 · 10−9 m
m
= 1, 0022 · 10−5
20 SkT
SkT
Das ergibt dann einen Fehler (95%iges Vertrauensniveau) von
sn
un = τ · √ = 1, 5623, mit τ = 2, 131
16
Da
λ
ohne Fehler als gegeben anzusehen ist und auch der Fehler des Hell-Dunkelzählers durch seine groÿe
Empndlichkeit wohl der ausschlaggebende ist, panzt sich auch nur dieser fort.
∂k λ
m
uk = · un =
· un = 4, 9431 · 10−8
.
∂n
20
SkT
Damit lässt sich der Kalibrierungsfaktor angeben
k = (1, 002 ± 0, 005) · 10−5
2.2
m
m
= 1, 002 · (1 ± 0, 5%) · 10−5
SkT
SkT
Bestimmung verschiedener Kohärenzlängen
Im Folgenden werden die Kohärenzlängen des Lichtes einer Glühlampe und einer Hg-Höchstdrucklampe
gemessen. Hierzu wird der Spiegel in eine Position gebracht, so dass der Gangunterschied der Teilstrahlen
4
nur sehr klein ist. Hier sind am ehesten Interferenzerscheinungen der Lichtquellen zu erwarten. Nun wird
die Spiegelposition gesucht in der die Interferenz einsetzt. Anschlieÿend wird die Position gesucht in der
die Interferenz wieder aussetzt. Der gemessene optische Weg entspricht nun der doppelten Kohärenzlänge
des Lichtes. Da aber die mechanische Weglänge ebenfalls einer doppelten optischen Weglängenänderung
entspricht, hebt sich der Faktor zwei auf und die Kohärenzlänge entspricht der Längendierenz der beiden
Spiegelpositionen.
In der folgenden Tabelle steht
xB
für die Position an der die Interferenz beginnt, und
xE
für die Position
bei der die Interferenz endet.
Tabelle 2: Messung zur Kohärenzlänge
Glühlampe
Hg-Lampe
xB
in Skt
xE
in Skt
xHg = xE − xB
xB
in Skt
in Skt
xE
in Skt
xGl = xE − xB
1523,0
1539,0
16,0
1529,0
1531,0
2,0
1521,0
1540,0
19,0
1528,5
1531,0
2,5
1521,0
1540,0
19,0
1528,5
1531,0
2,5
1522,0
1539,0
17,0
1529,0
1531,0
2,0
1521,0
1540,0
19,0
1529,0
1530,5
1,5
1521,0
1539,0
18,0
1529,0
1531,0
2,0
1522,0
1540,0
18,0
1528,5
1531,0
x̄Hg
Standardab. sxHg
Mittelwert
uxHg und uxGl
Für die Fehler
x̄Gl
Standardab. sxGl
18,00
Mittelwert
1,1547
in Skt
2,5
2,14
0,3780
ergibt sich:
Sx
Sx
uxHG = τ · √Hg = 1, 0680 SkT und uxGl = τ · √Gl = 0, 3496 SkT
7
7
Um die Kohärenzlängen zu erhalten, müssen die Längendierenzen noch mit dem Kalibrierungsfaktor multipliziert werden:
lHg = k · xHg = 1, 8036 · 10−4 m
lGl = k · xGl = 2, 1443 · 10−5 m
Für die Fehler gilt
∂lHg ∂lHg uk = k · ux + xHg · uk = 1, 160 · 10−5 m
ulHg = ux +
Hg
∂xHg Hg ∂k ∂lGl ux + ∂lGl uk = k · ux + xGl · uk = 3, 610 · 10−6 m
ulHg = Gl
Gl
∂xGl
∂k Damit lassen sich die Kohärenzlängen angeben mit
lHg = (1, 80 ± 0, 12) · 10−4 m
lGl = (2, 1 ± 0, 4) · 10−5 m
Im Stöcker, Taschenbuch der Physik wird für eine Quecksilberdampampe ein Richtwert für die Kohärenzlänge von
5 · 10−4 m
angegeben. Zumindest die Gröÿenordnung stimmt mit unserer Messnung über ein. Für
eine Glühlampe habe ich keinen Richtwert gefunden.
5
2.3
Schwebung der Na-D Linie
Als Schwebung versteht man die Überlagerung zweier Schwingungen oder Wellen, deren Frequenzen nur wenig
von einander abweichen. Das Licht einer Na-Lampe enthält zwei dicht beieinander liegende Spektrallinien
mit
λ1 = 589, 00 nm
und
λ2 = 589, 59 nm.
Falls die Lage des beweglichen Spiegels verändert wird, treten
Schwebungserscheinungen auf. Die Interferenzringe sind sehr kontrastreich oder verschwinden. Wenn man
den Abstand zweier Minima bestimmt, erhält man die Schwebungswellenlänge. Da allerdings immer nur die
Hälfte des eigentlichen optischen Weges gemessen wird, muss auch hier die Dierenz der Minima mit dem
Faktor zwei versehen werden.
Tabelle 3: Messung der Schwebungswellenlänge
Lage der Minima
xi
in SkT
Dierenz
d = xi − xi−1
1602,0
29,0
1573,0
29,5
1543,5
28,5
1515,0
30,0
1485,0
29,0
1456,0
28,5
1427,5
29,0
1398,5
28,5
1370,0
29,0
in SkT
1341,0
d¯
Standardab. sd
Mittelwert
29,0
0,5
Die Schwebungswellenlänge ergibt sich nun aus dem Doppelten des Abstandes der Minima und multipliziert mit dem Kalibrierungsfaktor k.
λs = 2 · d · k = 2 · 29, 0 SkT · 1, 002 · 10−5
Der Fehler für
d
m
= 5, 8116 · 10−4 m.
Skt
ergibt sich aus
sd
ud = τ · √ = 0, 3854 Skt mit τ = 2, 306.
9
Für den Fehler von
λs
uλs
ergibt sich
∂λs ∂λs · ud = 2 · d · uk + 2 · k · ud = 1, 0916 · 10−5 m.
· uk + =
∂k ∂d Die Schwebungswellenlänge lässt sich nun angeben
λs = (5, 81 ± 0, 11) · 10−4 m.
Für die Schwebungsfrequenz gilt
νs = ν1 − ν2
mit
ν=
c
λ ergibt sich die Beziehung
c
c
c
=
−
λs
λ1
λ2
Nimmt man nun die Na-D2 Linie als bekannt an (λ2
= 589, 59 nm,
Geschke: Physikalisches Praktikum,
Tabelle 13) , so gilt für die erste Spektrallinie
λ1 =
c
λs
c
+
c
λ2
=
λ s λ2
= 5, 88992 · 10−7 m.
λs + λ 2
6
Der Fehler ergibt sich aus:
uλ1
∂λ1 uλs = λ2 (λs + λ2 ) − λs λ2 uλs = 1, 1305 · 10−11 m
=
∂λs (λs + λ2 )2
Damit lässt sich die Na-D1 Linie angeben mit
λ1 = (588, 992 ± 0, 011) nm.
Aus Dieter Geschke: Physikalisches Praktikum Tabelle 13 ist die D1 Linie mit
λ1 = 589, 00 nm
angegeben.
Damit liegt der akzeptierte Wert in der Vertrauensgrenze. Für die Wellenlängendierenz der beiden Linien
ergibt sich:
∆λ = λ2 − λ1 = 0, 598 nm
Der Fehler der Dierenz besteht hier nur aus dem Fehler von
λ1 .
Damit lässt sich die Dierenz angeben mit
∆λ = (0, 589 ± 0, 011) nm
2.4
Bestimmung der Dicke eines Mikroskopdeckgläschens
Um die Dicke des gegebenen Glasplättchens zu bestimmen, wird die optische Wegdierenz zwischen den Wegen des Lichtes ohne und mit Plättchen betrachtet. Als Lichtquelle nutzen wir die Glühlampe. Als Bezugspunkt dient die Position des Spiegels bei der die Interferenz gerade aussetzt. Stellt man nun das Glasplättchen
in den Strahlengang, so muss das Licht einen optisch längeren Weg zurück legen, da die Lichtgeschwindigkeit
im Inneren kleiner ist. Also muss ebenfalls der Weg zum beweglichen Spiegel vergröÿert werden, um wieder
die Position zu erreichen in der die Interferenz gerade aussetzt.
Die Strecke, um die sich der optische Weg verlängert ist durch die Beziehung
l = d · (nGlas − nLuf t )
gegeben, wobei
d
die Dicke des Glasplättchens ist. Dabei ist durch den Term
(nGlas − nLuf t )
berücksichtigt,
dass das Licht auch ohne Glasplättchen einen längeren Weg zurück legen würde. Da das Licht das Glasplättchen zweimal durchläuft (vor und nach der Reektion am Spiegel) kompensiert sich der Faktor 2, der
normalerweise bei Längenmessungen zu berücksichtigen ist.
Tabelle 4: Messung zur Dicke eines Mikroskopdeckgläschens
xo
in SkT (ohne Plättchen)
xm
in SkT (mit Plättchen)
1539,5
8,5
1531,0
1540,0
9,0
1531,0
1539,5
8,5
1530,5
1539,5
9,0
1531,0
1539,5
8,5
1531,0
1539,5
Mittelwert
¯l
Standardabweichung
Der Fehler für
l
l = xm − xo in
1531,0
ergibt sich zu
Skt
8,5
8,67
sl
0,2582
sl
ul = τ · √ = 0, 2710 SkT
6
Die Dicke des Plättchens ergibt sich aus
d=
l
8, 67 SkT
m
·k =
· 1, 002 · 10−5
= 1, 6862 · 10−4 m.
(nGlas − nLuf t )
1, 515 − 1
SkT
7
Der Fehler ergibt sich aus
∂d ∂d 1
ud = ul + uk =
(k · ul + l · uk ) = 6, 1140 · 10−6 m.
∂l
∂k
(nGlas − nLuf t )
Damit lässt sich die Dicke des Plättchens angeben:
d = (1, 69 ± 0, 07) · 10−4 m.
8