Vorlesung 12

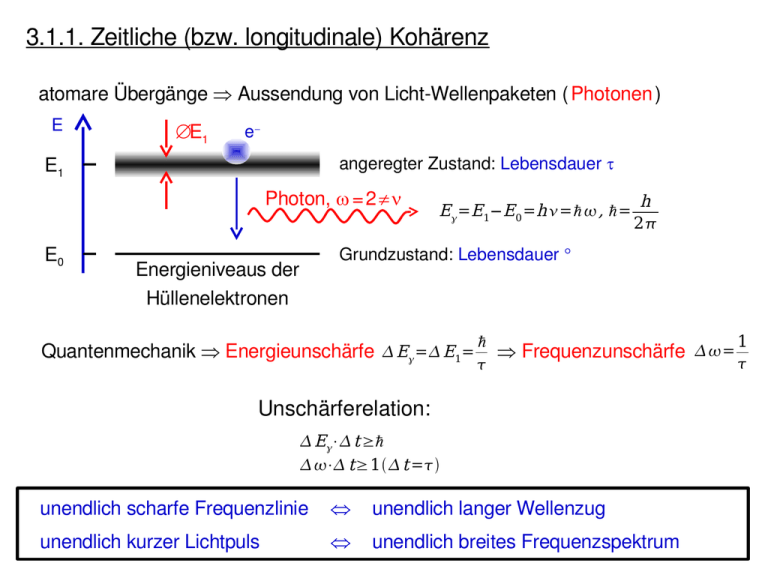
3.1.1. Zeitliche (bzw. longitudinale) Kohärenz
atomare Übergänge ⇒ Aussendung von Licht­Wellenpaketen ( Photonen )
E
∆ E1
e−
E1
angeregter Zustand: Lebensdauer τ
Photon, ω = 2 π ν
E0
Energieniveaus der Hüllenelektronen
E=E1−E0 =h =ℏ  , ℏ=
h
2
Grundzustand: Lebensdauer ∞
ℏ
1
 =
 E= E1=
Quantenmechanik ⇒ Energieunschärfe ⇒ Frequenzunschärfe

Unschärferelation:
 E⋅ t ≥ℏ
 ⋅ t ≥1 t =
unendlich scharfe Frequenzlinie ⇔
unendlich langer Wellenzug
unendlich kurzer Lichtpuls ⇔
unendlich breites Frequenzspektrum

I 
 =2  =
1

1
 t K=
=2 

“Strahl 2”
“Strahl 1”
Kohärenzlänge ∆ℓK ist der Gangunterschied (Abstand phasengleicher Punkte) zwischen Strahl 1 und 2, der während der Kohärenzzeit auftritt:
 0−

2
0
 0

2

1 2 2
c
1
 ℓ K =c  t K =
=
=
≈

1  


Andere Interpretation (siehe nächste Folie):
Frequenzspektrum => Bereiche, die aussehen wie Ausschnitte einer Sinuswelle
(dazwischen “unvorhersagbarer” Phasensprung): Wellenzüge
Kohärenzlänge ≃ endliche Länge von Wellenzügen
Bsp.: Überlagerung von 6 Sinuswellen gleicher Richtung und Amplitude
Wellenlängenbereich ∆λ
400 nm bis 410 nm
Kohärenzlänge (in Wellenlängen)
Etwa 30 ( λ2 /∆λ = λ 400/10)
Wellenzug
etwa 11
400 nm bis 430 nm
400 nm bis 500 nm
etwa 5
Spalte Welle in zwei Teilwellen auf und bringe sie am Ort P zur Überlagerung.
Identische Wellenzüge beider Teilwellen überlagern sich nur, wenn sich Laufwege beider Teil­
wellen nicht mehr als die Länge der Wellenzüge unterscheiden ­­> nur dann Interferenz möglich
Teilwelle, die um mehr als ∆ℓK verschoben wurde
Aus: Kohärenz von Licht, Der Karlsruher Physikkurs, Gerhardt Anzt
Beispiele:
1) Mittlere Lebensdauer eines angeregten Atoms τ=O(10­9­10­8 s) => ∆ℓK= c τ ≈O(m)
a) Atome in Dampflampe: thermische Bewegung => Doppler­Effekt => Frequenz/Dopplerverbreiterung
b) Große Dampfdichte: Erzwungene Emission angeregter Atome durch Stöße mit tStoß< τ (Stoß­Verbreiterung) => ∆ℓK≈ O(cm)
Falls Gangunterschied von Wellenzügen zweier aufgespaltener Teilwellen > ∆ℓK: an Wellenzügen verschiedene Atome beteiligt, deren Emission keine feste Phasenbeziehungen haben => zeitliche Inkohärenz
< > 2
2) Taschenlampe: λ ≈ 400 … 700 nm  ℓ K=
=O   m 


⟨λ⟩ ≈ 550 nm 3) Laser ( Light Amplification by Stimulated Emission of Radiation )
E
E1
E0
e−metastabiler Zust.: τ → ∞
e−
Grundzustand: τ = ∞
Spontane Emission
Induzierte Emission
CO2­Laser: λ ≈ 10,6 µ m, ∆ λ ≈ 10−5 nm ⇒ ∆ ℓK ≈ 11 km
3.1.2. Räumliche (bzw. laterale) Kohärenz
Definition: Ändert sich die räumliche Differenz ∆
Definition:
rϕ = ϕm(r1) – ϕm(r2) der Phase ϕm einer beliebigen Teilwelle Em während Beobachtungszeit ∆t um weniger als 2π, dann heißt das Wellenfeld räumlich kohärent.
Definition: Kohärenzfläche = Fläche senkrecht zur Ausbreitungsrichtung mit
relativen Phasenmischungen ∆ ϕ < 2 π bzgl. Interferenzpunkt.
Kohärenzvolumen = Volumen mit lateraler und longitudinaler Phasenmischung ∆ ϕ < 2 π bzgl. Interferenzpunkt.
Nur innerhalb des Kohärenzvolumens können Interferenzstrukturen beobachtet werden !
3.1.2. Räumliche (bzw. laterale) Kohärenz
Monochromatische Lichtquelle mit unterschiedlichen Ausbreitungsrichtungen:
Senkrecht zur Referenzausbreitungsrichtung
laufen die zeitlich kohärenten Wellen in der Phase auseinander.
Laserlicht hat neben einer hohen zeitlichen auch eine hohe räumliche Kohärenz:
∞
Kohärenzflächen (mit ∆ ϕ=0)
ideale ebene Welle
Kohärenz­
fläche
4 π r2
reale Quelle
ideale Kugelwelle Beispiel: Sonne, Beteigeuze ( Orion )
3.1.3. Erzeugung kohärenter Wellen
a) Phasenstarre Sender:
b) Strahlteilung:
∼
möglich mit akustischen Wellen
c) Virtuelle Mehrfachbilder einer Quelle:
Inter­
ferenz
L1
L
L2
2
2
2 E0 cos 
 
r

2
3.2.1. Zweistrahlinterferenz
z0
3.2. Interferenz
Voraussetzung: Interferenz von Strahlen aus einem Kohärenzvolumen
3.2.1. Zweistrahlinterferenz
z0
Beispiel 1: Der Fresnel­Spiegel Punktlichtquelle L (y=0) bestrahle Spiegel S1 und S2, die den Winkel ε miteinander bilden. Licht auf Schirm im Punkt P(x,y,z=0) scheint von den punktförmigen virtuellen Lichtquellen L1,2 zu kommen. 2
2
2
Weglängen: LS1 P=L1 P=  x d   y  z0
LS2 P=L2 P=  x −d 2  y 2 z20
 s =  x d2 y2 z20 − x −d 2 y 2 z20
Alle Punkte P(x,y,z=0) mit ∆s=const. liegen auf Hyperbel (ohne Beweis)
3.2.1. Zweistrahlinterferenz
 s =m⋅  m=0,±1,±2, ...
Beide Teilwellen in Phase für Imax =c 0  E1 E2 2
=> Maximale Intensität: (schwarze Punkte)
2m1⋅
 s=
Beide Teilwellen gegenphasig für 2
2


=> Minimale Intensität: Imin = c 0  E1 −E2 
z0
=> Räumliches Intensitätsmuster in x­y­Ebene aus hellen und dunklen Hyperbeln
Räumliche Ausdehnung des Interferenzmusters auf Schirm durch Kohärenzlänge bestimmt:
a) ∆ν: spektrale Bandbreite der Lichtquelle b) Abstand zu den virtuellen Lichtquellen L1 und L2 3.2.1. Zweistrahlinterferenz
Bemerkungen:
1) Nichtchromatisches Licht: Nebenmaxima zeigen Farbsäume
a) Warum?
b) Wie ist die Farbfolge von Innen nach Aussen?
2) Ausmessung der Maxima(Minima) erlaubt Bestimmung von λ monochromatischen Lichts
3) Einfluss der Ausdehnung der Lichtquelle auf Kohärenz anhand des nächsten Beispieles