§1 Plancks Strahlung schwarzer Körper Historisch ist die

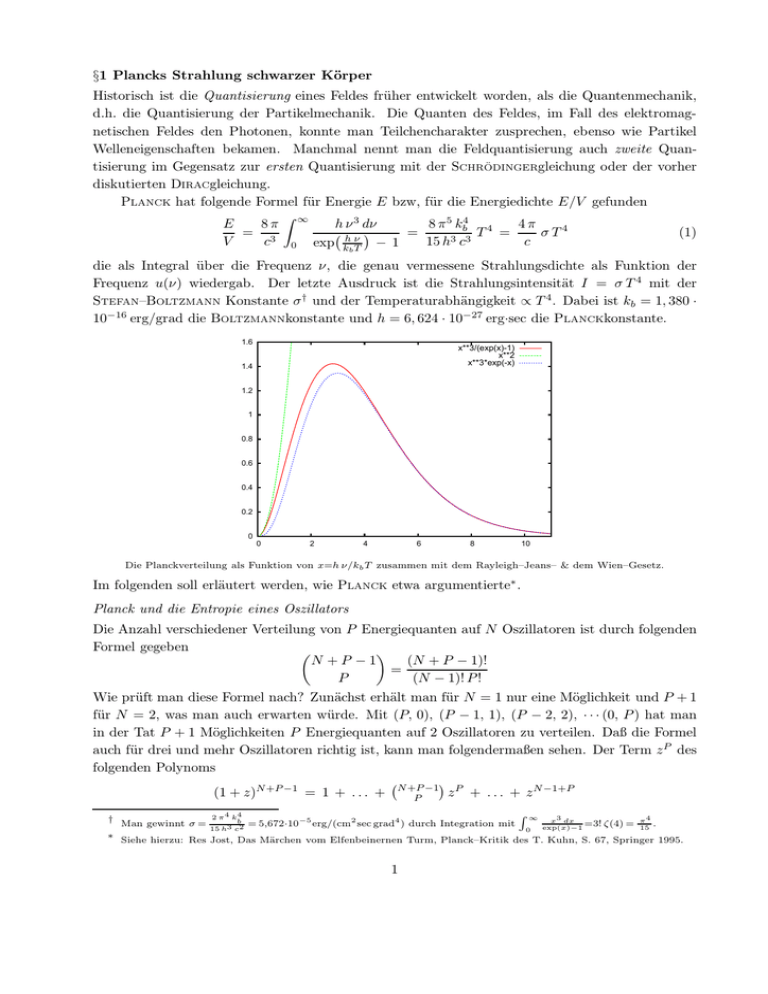
§1 Plancks Strahlung schwarzer Körper
Historisch ist die Quantisierung eines Feldes früher entwickelt worden, als die Quantenmechanik,
d.h. die Quantisierung der Partikelmechanik. Die Quanten des Feldes, im Fall des elektromagnetischen Feldes den Photonen, konnte man Teilchencharakter zusprechen, ebenso wie Partikel
Welleneigenschaften bekamen. Manchmal nennt man die Feldquantisierung auch zweite Quantisierung im Gegensatz zur ersten Quantisierung mit der SCHRÖDINGERgleichung oder der vorher
diskutierten DIRACgleichung.
PLANCK hat folgende Formel für Energie E bzw, für die Energiedichte E/V gefunden
Z
8 π 5 kb4 4
h ν 3 dν
8π ∞
4π
E
=
= 3
T =
σ T4
(1)
h
ν
3
3
V
c 0 exp k T − 1
15 h c
c
b
die als Integral über die Frequenz ν, die genau vermessene Strahlungsdichte als Funktion der
Frequenz u(ν) wiedergab. Der letzte Ausdruck ist die Strahlungsintensität I = σ T 4 mit der
STEFAN–BOLTZMANN Konstante σ † und der Temperaturabhängigkeit ∝ T 4 . Dabei ist kb = 1, 380 ·
10−16 erg/grad die BOLTZMANNkonstante und h = 6, 624 · 10−27 erg·sec die PLANCKkonstante.
1.6
x**3/(exp(x)-1)
x**2
x**3*exp(-x)
1.4
1.2
1
0.8
0.6
0.4
0.2
0
0
2
4
6
8
10
Die Planckverteilung als Funktion von x=h ν/kb T zusammen mit dem Rayleigh–Jeans– & dem Wien–Gesetz.
Im folgenden soll erläutert werden, wie PLANCK etwa argumentierte∗ .
Planck und die Entropie eines Oszillators
Die Anzahl verschiedener Verteilung von P Energiequanten auf N Oszillatoren ist durch folgenden
Formel gegeben
N +P −1
(N + P − 1)!
=
(N − 1)! P !
P
Wie prüft man diese Formel nach? Zunächst erhält man für N = 1 nur eine Möglichkeit und P + 1
für N = 2, was man auch erwarten würde. Mit (P, 0), (P − 1, 1), (P − 2, 2), · · · (0, P ) hat man
in der Tat P + 1 Möglichkeiten P Energiequanten auf 2 Oszillatoren zu verteilen. Daß die Formel
auch für drei und mehr Oszillatoren richtig ist, kann man folgendermaßen sehen. Der Term z P des
folgenden Polynoms
P
−1
(1 + z)N +P −1 = 1 + . . . + N +P
z + . . . + z N −1+P
P
†
∗
Man gewinnt σ =
2 π 4 k4
b
15 h3 c2
= 5,672·10−5 erg/(cm2 sec grad4 ) durch Integration mit
R∞
0
4
x3 dx
=3! ζ(4) = π
15
exp(x)−1
.
Siehe hierzu: Res Jost, Das Märchen vom Elfenbeinernen Turm, Planck–Kritik des T. Kuhn, S. 67, Springer 1995.
1
hat den zu erklärenden Binomialkoeffizienten als Vorfaktor. Nimmt man N = 3 an, dann ist ein
Term z P durch Ausmultiplikation von (1 + z)2+P enstanden, so daß er zwei Einsen enthält
z P1 1 z P2 1 z P3
mit P1 + P2 + P3 = P ,
wobei die Pi eine spezielle Aufteilung der P Quanten auf die drei Oszillatoren geben. Nach dem Bi
nominalformel gibt es davon N +2+P
Terme. Man braucht also N −1 “Einsen” um eine Aufteilung
P
der Energie unter N Oszillatoren zu bekommen.
Mit der BOLTZMANNkonstanten kb erhält man für die Entropie
−1
SN /kb = ln N +P
≈ (N + P − 1) ln(N + P − 1) − (N − 1) ln(N − 1) − P ln P
P
mit Hilfe der STIRLINGformel ln N ! ≈ N ln(N/e) unter der Voraussetzung, daß N und P große
Zahlen sind. Mit P = Egesamt /(h ν), wobei Egesamt die auf die N Oszillatoren zu verteilende
Energie ist, bekommt mit E = Egesamt /N für den Quotienten P/N = E/(h ν) die mittlere Anzahl
der Energiequanten pro Oszillator. Die Entropie pro Oszillator ist S = SN /N und nach der
vorherigen Formel
S(E)
= hEν + 1 ln hEν + 1 − hEν ln hEν
kb
Dies ist PLANCKs Entropieformel für einen harmonischen Oszillator, die für große Energie E ≫ h ν
sich in die “klassische” Form
S̃(E)
e
= ln E
k
hν
verwandelt. Mit der Formel dS/dE = 1/T kann mit die Entropieformel von PLANCK in eine
bekanntere Form umwandeln
hν hν
1
1
hν
hν
(2)
⇒ exp
−1 =
=
ln 1 +
⇒ E = h ν/k T
kT
hν
E
kT
E
e
−1
Der entscheidende Schritt ist tatsächlich die Quantelung der Energie. Mit der Kombinatorik kann
man mit Hilfe der Formel S = k ln W die Entropie bestimmen, so ähnlich wie man die Mischungsentropie bei Lösungen bestimmt, mit denen sich PLANCK vorher beschäftigt hatte, ehe er das Problem
der Hohlraumstrahlung studiert hat. . .
Die Plancksche Formel
Um die Formel (1) zu bekommen, muß man nur die die Beiträge der vielen Oszillatoren aufsummieren, wobei Gl.(2) der Beitrag eines einzelnen Oszillators ist. Die Oszillatoren zählt man am
einfachsten in einem kubischen Hohlraum mit dem Volumen L × L × L. Die Wellenzahl–Vektoren
der Schwingung sind ~k = 2Lπ ~n mit ~n = (n1 , n2 , n3 ) und ni = 0, ±1, ±2 . . . entsprechend periodischen Randbedingungen. Die zugehörige Frequenz ist ν = 2 π c |~k|. Alle Schwingungen bekommt
man durch Summation über die ganzen Zahlen ni , d.h.
Z
Z
Z
Z ∞
Z inf ty
XXX
2
3
· · · ≈ dn1 dn2 dn3 · · · = 4 π
n dn · · · = 4 π (L/c)
ν 2 dν · · ·
(3)
n1
n2
0
n3
0
h ν/k T
wobei · · · für die zu integrierende Funktion h ν/(ep
− 1) steht. Die zweite Umformung ist
der Übergang zur Integration über den Radius n = n21 + n22 + n23 . Da die Frequenz ν = c n/L ist
ergibt sich die letze Umformung daraus.
Formel (1) ist durch die letzten Form des Integrals (3) gegeben. Man muß nur noch berücksichtigen, daß es zwei Polarisationen für jeden Zusstand gibt und L3 = V ist.
2