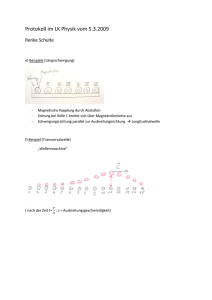
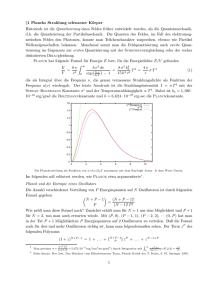
Synchronisation

Synchronisation
Philipp Kroeger
Inhaltsverzeichnis
●
●
●
●
Einleitung / Motivation
–
Geschichtliches
–
Erste wissenschaftliche Zugänge und Probleme
–
Das Kuramoto­Modell 1975
Synchronisation als Konsequenz
–
Zwei gekoppelte Oszillatoren
–
Situation bei N gekoppelten Oszillatoren
Beispiele
–
Synchronisierter Spaziergang auf der Millennium Bridge –
Supraleitung –
Asteroidengürtel –
Synchronisation von chemischen Oszillatoren
Zusammenfassung und Quellen
Geschichtliches
●
●
Entdeckung durch Huygens 1665, beobachtet an neuen, genaueren Uhren.
Seit 300 Jahren berichten Reisende von „plötzlich leuchtenen Glühwürmchenschwärmen“.
Erste wissenschaftliche Zugänge und Probleme
●
●
●
1915­1935, insg. 20 Artikel zum Thema Synchronisation, kontrovers diskutiert, wenig beachtet.
1950 Mathematiker Norbert Wiener, Wegbereiter durch Ideen zu Zufallsprozessen, weckte erst Bemühungen, sah Gemeinsamkeit von Alphawellen, Lücken in Asteroidengürteln, Grillen, Generatoren 1960 John Buck macht Versuche an Leuchtkäfern, bemerkte die Tendenz zur „Anpassung“ der Eigenfrequenz. Erste wissenschaftliche Zugänge und Probleme
●
1964 Art Winfree, Mathematiker/Biologe, stellte Gleichungen am Computer auf, unter bestimmten Bedingungen stellte er Synchronisation fest, unabhänging vom Startpunkt im Phasenraum
Das Kuramoto­Modell ●
1975 Physiker Yoshiki Kuramoto beschäftigte sich zielstrebig mit Winfree´s Arbeit, ausgehend von: erarbeitete er mit Einführung eines gemeinsamen mittleren Feldes: Im Weiteren erhält er einen Fixpunkt für Oszillatoren nahe dem Verteilungsmaximum. Gegeben durch:
Der Rest der Oszillatoren gehört zum asynchronen Ensemble Das Kuramoto­Modell
●
Im Fall großer Kopplung/Gesamtamplitude ist die Synchronisation möglich (eingschlossener Bereich). Außerdem folgt ein Maß der Ordnung, d.h. Verhältnis von synchronen Oszillatoren zur Gesamtzahl
Zwei gekoppelte Oszillatoren
●
●
●
Synchronisation als Endzustand zweier (fast) gleicher, gekoppelter „integrate­and­fire“ Oszillatoren
Bild entspricht einem Pointcareschnitt aus dem Phasenraum, Geschwindigkeiten sind hier nicht explizit enthalten
0­ Osz.1 bei null, 1­ Bewegung bis Osz. 2 feuert, 2­ Osz.2 nun bei null mit Phasenschift für Osz.1, 3­ Bewegung bis Osz.1 feuert mit Phasenschift für Osz.2, 4­ Kreislauf beginnt von vorne, endet in der Winkelhalbierenden
Situation bei N gekoppelten Oszillatoren
●
Nur für Kopplungen oberhalb eines bestimmten Grenzwertes.
●
Es verstärkt sich das mittlere Feld K – bis zu einem normierten Maximum. ●
K dient also als Ordnungsparameter
●
„Phänomen“ der Synchronisation schwer zu beabachten, perfekt bei identischen Oszillatoren
Synchronisierter Spaziergang auf der Millennium Bridge
●
●
●
●
Phänomen bei Einweihung einer Londoner Brücke
Viele Besucher liefen im Takt der schaukelnden Brücke.
Anfängliche Vermutungen – es liege am Design, an Resonanzeigenschaften – erwiesen sich als falsch
Computermodelle lieferten hier Aufklährung Synchronisierter Spaziergang auf der Millennium Bridge
●
●
●
Das Modell der Brücke ist ein harmonischer, gedämpfter Oszillator mit äußerer Anregung
Anregung entspricht einer realistischen Verteilung von Impulsen durch Schritte
a­ steigende Zahl N an Passanten b­ Auslenkungsamplitude der Brücke in Abhängigkeit von N c­ Anteil an synchron laufenden Passanten
Supraleitung
●
●
●
●
●
1957 Lean Cooper et. al. Erklähren die Superleitfähigkeit über Elektronenpaare.
Elektronen sind Fermionen Nur in einem synchronisierten Ensemble (Einstein­Bose­Kondensat) verhalten sie sich identisch.
Bei extrem tiefen Temperaturen: Kopplung indirekt über Verformungen der Gitterstruktur durch Ladungsverschiebungen. Bei Stößen an dem Gitter (d.h. Wiederstand) werden Elektronen frei, die sich tendenziell dem BEK anschließen → verminderter Widerstand
Asteroidengürtel ●
●
●
●
Zwischen Mars und Jupiter, insgesamt nur 1/20 der Mondmasse ­ überraschend wenig. Kirkwood entdeckte 1857 Lücken in dem Asteroidengürtel
Lücken sind nicht äquidistant, zeigen aber dennoch Struktur.
Jupiter wirkt für bestimmte Orbitale als Katapult Asteroidengürtel ●
●
Systematische Wechselwirkung zwischen Jupiter und Asteroid bei bestimmten Asteroidorbitalen
Mit steigendem Radius der großen Halbachse wirkt die Massenverteilung ausgedünnt, trotz zunehmendem Raum mit steigendem Radius
Synchronisation von chemischen Oszillatoren
●
●
●
●
Integrate and fire – Oszillatoren bilden als gekoppeltes Ensemle den Taktgeber der Herzens
1980 Michael Russell und Genevieve Switz entdeckten Synchronisation bei der Menstruation in Kontakt stehender Frauen (Unterschiede von 9,3Tage reduzierten sich auf 3,4)
Einzellige Pilzkulturen besitzen die Fähigkeit zur Kopplung über chemische Stoffe
Die Leuchtmechanismen der Leuchtkäfer sind chemischer Art und unterliegen einer Kopplung durch Licht.
Die Glühwürmchen
Zusammenfassung
●
●
Es gibt Zwischenstadien mit Ordnungsparametern ●
Durch Unscheinbarkeit häufig übersehen
●
Bei ausreichend starker Kopplung neigen weitesgehend gleiche Oszillatoren zu synchronem Verhalten.
Kopplungsfähige Bereiche im Raum aller Oszillatoren bilden Ordnung d.h. Selbstorganisation
Quellen
●
●
●
●
●
Sync / Steven Strogatz / Hyperion­Verlag NY – 2003
Coupled oscillators and biological synchronization / S. Strogatz, Ian Stewart /Scientific American Vol 269 Nr.6
Synchronisation eines hierachischen Ensembles global gekoppelter selbsterregter Oszillatoren / Diplomarbeit von Cornelia Petrović / Münster 2007
Dynamical quorum sensing and synchronization in large populations of chemical oszillators / Science 30.1.2009
Crowd synchrony on the Millennium Bridge / nature Vol 438 3.Nov 2005
Danke für´s Zuhören