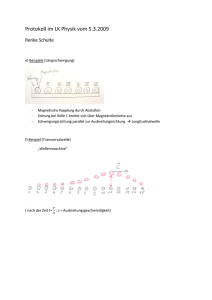
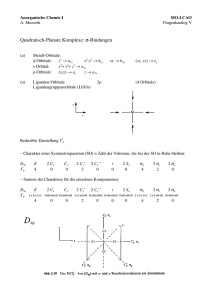
n - CCP14
Werbung

„Gekoppelte Oszillatoren“ Inhalt • Gekoppelte Pendel • Gekoppelte elektrische Schwingkreise • Gekoppelte Schwingungen in den Bausteinen der Materie – Orbitale der Elektronen – Molekülschwingungen – Schwingungen in Festkörpern Feder und Massenpunkt Einheit F k s F m s k s m s Bezeichnung 1N Federkraft 1N d‘ Alembertsches Trägheitskraft Prinzip 1N Schwingungsgleichung Erste Eigenschwingung der über eine Feder gekoppelten Oszillatoren Leicht erhöhte Frequenz: Kopplungsfeder wird wenig beansprucht Symmetrische Auslenkungen Zweite Eigenschwingung der über eine Feder gekoppelten Oszillatoren Höhere Frequenz: Kopplungsfeder wird stark beansprucht Anti-Symmetrische Auslenkungen Versuch: Gekoppelte Pendel • Verhalten eines einzelnen Schwingkreises • Kopplung über die Feder • Schwebungen durch Überlagerung von zwei Schwingungen unterschiedlicher Frequenz • Suche nach den Eigenfrequenzen durch spezielle Startbedingungen • Unterschiedliche Eigenschwingungen zeigen unterschiedliche Symmetrie „Schlüsselexperiment“ Doppelpendel Schwingungart Symmetrie bei Spiegelung Erste Eigenschwingung Symmetrisch Zweite Eigenschwingung „Anti“-symmetrisch Beliebig, das ist eine Überlagerung beider Eigenschwingungen Unsymmetrisch Muster Effekt der Kopplung • Ohne Kopplung: Beide Oszillatoren zeigen die gleiche Eigenfrequenz • Mit Kopplung: – Zwei „Schwingungsmoden“ mit unterschiedlichen Eigenfrequenzen – Die Symmetrie der Auslenkungen beider Moden ist unterschiedlich Versuch: Gekoppelte elektrische Schwingkreise • Verhalten eines einzelnen Schwingkreises • Kopplung über die Feldstärken • Schwebungen durch Überlagerung von zwei Schwingungen unterschiedlicher Frequenz • Suche nach den Eigenfrequenzen mit Fourier-Analyse Kopplung von zwei elektrischen Schwingkreisen über das magnetische Feld Kopplung ohne Materie gibt es nur in elektromagnetischen Feldern! Über das Magnetfeld gekoppelte Schwingkreise • Schwebungen aufgrund des Austauschs der Energie zwischen den Schwingkreisen • Grund: Überlagerung der beiden Eigenschwingungen mit – leicht unterschiedlichen Frequenzen – unterschiedlichen Symmetrie-Eigenschaften • Erste Eigenschwingung mit „gleichphasigen“ Feldstärken in beiden Kreisen • Zweite Eigenschwingung mit „gegenphasigen“ Feldstärken in beiden Kreisen Gekoppelte Schwingungen in der Materie • Alle durch Wechselwirkungskräfte verbundenen Teile sind – bei entsprechender Anregung – „gekoppelte Pendel“ • Bei Teilchenzahl n wächst - im dreidimensionalen Raum - die Zahl der „Freiheitsgrade“ auf 3n • Es gibt deshalb 3n Eigenschwingungen mit unterschiedlichen – Symmetrie-Eigenschaften – Energie-Werten • An jeder Eigenschwingung sind immer alle Oszillatoren beteiligt Beispiele • • • • „Gekoppelte Pendel“ Orbitale des Elektronensystems Molekülschwingungen Schwingungen im Festkörper, „Phononen“ Orbitale • Die Elektronen in einer „Schale“ n eines Atoms bilden ein System identischer, gekoppelter Oszillatoren – Hier verlässt man das Bohrsche Atommodell • Die Eigenschwingungen dieses Systems werden mit den Quantenzahlen l, m bezeichnet – und zeigen unterschiedliche Symmetrie-Eigenschaften • Orbitale zeigen die Aufenthaltswahrscheinlichkeit der Elektronen – was bei Oszillatoren sinnvoll ist Symmetrie der drei p Orbitale einer Unterschale (l=1) bei beliebiger Drehung um eine Achse Drehung erlaubt? X-Achse Y-Achse Z-Achse Ja Nein Nein Nein Ja Nein Nein Nein Ja Orbitale mit ihren Quantenzahlen l 1 Symmetrie m0 m 1 t1 g m 1 Beispiel: Orbitale im Neon HauptDrehimpuls- oder quantenzahl Nebenquantenzahl OrientierungsMax. Zahl Quanten- der Zustände zahl Schale, Orbital l m l Spin Typ N Schale 0 l N 1 1 K 0 s 0 0 s 0 2 L -1 1 p 0 1 2 2 6 Form der Orbitale Molekülschwingungen, Beispiel CO2, erste Streckschwingung, symmetrisch z x Beispiel CO2, zweite Streckschwingung antisymmetrisch z x Beispiel CO2, erste Deformationsschwingung z x Beispiel CO2, erste Deformationschwingungen, Ansicht von der Längs-Seite z y Beispiel CO2, zweite Deformationschwingung, Ansicht von der Längs-Seite z y Symmetrieeigenschaften dieser Schwingungen bei der Einheitsoperation, Drehung und Spiegelung 1 ja ja ja ja ja nein nein ja ja nein ja nein Ist die Schwingung invariant gegenüber der Symmetrieoperation? Beispiel: Anregung der ersten Deformationsschwingung von CO2 im Infrarot-Bereich Kristalline Festkörper • Bei n Teilchen gibt es n „Schwingungsmoden“ mit Auslenkungsmuster unterschiedlicher Symmetrie • Die n Eigenfrequenzen der Moden liegen zum Teil sehr dicht beisammen, es entstehen Energiebänder Modell für die Einheitszelle eines Kristalls mit zwei Atomen in der Elementarzelle mit Federn anstelle der Coulomb-Kräfte Freiheitsgrade eines Kristallgitters mit 2 Atomen in der Elementarzelle Beispiel für die Eigenschwingungen eines Kristalls mit zwei Atomen in der Elementarzelle Translation Innere Schwingung Freiheitsgrade eines Kristallgitters mit 2 Atomen in der Elementarzelle Beispiel für eine Eigenschwingung Phononen • Zu jedem Auslenkungsmuster gehört eine „Eigenfrequenz“ • Normalschwingungen der Teilchen in kristallinen Festkörpern werden „Phononen“ genannt • Die Schwingungen der Teilchen, die Phononen, koppeln an die Anregung der Elektronen Wirkung der Kopplung: Vergleich der Spektren von Gasen/Flüssigkeiten/Festkörpern C6H6 Beispiele für Emission und Absorption an freien Atomen und im Vergleich dazu – an heißen Festkörpern Absorptionslinien von Wasserstoff vor der „Weissen“ Strahlung der Sonne (an der Oberfläche ca. 6000 K) Abbildung: Emissionsspektrum der Quecksilberdampflampe und Absorptionslinien im Sonnenspektrum. Quelle: Meyers Enzyklopädisches Lexikon Zuammenfassung • Alle durch Wechselwirkungskräfte verbundenen Teile sind – bei entsprechender Anregung – „gekoppelte Pendel“ • Bei Teilchenzahl n wächst die Zahl der „Freiheitsgrade“ auf 3n • Es gibt deshalb 3n Eigenschwingungen mit unterschiedlichen – Symmetrie-Eigenschaften – Energie-Werten Finis Leicht erhöhte Frequenz: Kopplungsfeder wird wenig beansprucht Symmetrische Auslenkungen