4.4 Dispersion und Absorption von Licht

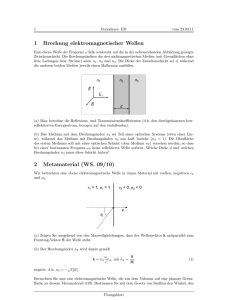
4.4. DISPERSION UND ABSORPTION VON LICHT
4.4
13
Dispersion und Absorption von Licht
In den vorhergehenden Abschnitten haben wir gesehen, dass der Brechungsindex n(k)
eine entscheidende Rolle bei der Ausbreitung von elektromagnetischen Wellen in Medien
spielt. In diesem Abschnitt werden wir für dünne Medien anhand eines einfachen Modells
den Ursprung und die Frequenzabhängigkeit des Brechungsindex herleiten. Bereits in
der Elektrodynamik haben wir festgestellt, dass die relative Dielektrizitätskonstante für
beispielsweise Wasser bei tiefen Frequenzen ω → 0 typischerweise Werte εr ∼ 80 annimmt.
√
Dementsprechend erwarten wir für niedrige Frequenzen einen Brechnungsindex n = εr ∼
9. In Verbindung mit dem empirischen Wert für den Brechungsindex von n = 1, 333,
bestimmt im sichtbaren Bereich bei λ = 589 nm, sehen wir sofort, dass der Brechungsindex
einer starken Frequenzabhängigkeit unterliegt.
Um diese Tatsache besser zu verstehen, werden wir die aufgrund des äußeren elektrischen
Feldes induzierte Polarisation betrachten. Wie zuvor nehmen wir an, dass die elektromagnetische Welle sich in z-Richtung ausbreitet, und dass das elektrische und magnetische
Feld in x- beziehungsweise y−Richtung zeigt. Im Rahmen eines einfachen Atommodells
werden wir die Atomkerne als stationär betrachten, und wir nehmen an, dass lediglich die
leichten Elektronen sich aufgrund der elektrischen Kraft bewegen werden. Die treibende
Kraft wird durch die Amplitude des elektrischen Feldes gegeben:
~
~ o exp (−iwt).
F~ (t) = −eE(t)
= −eE
(4.63)
Ohne externe Kraft führen die Elektronen für kleine Auslenkungen aus ihren Ruhepositionen harmonische Schwingungen mit charakteristischer Resonanzfrequenz ωo durch. Des
Weiteren nehmen wir eine schwache Dämpfung γ ¿ ωo an, die den Energieverlust der
harmonischen Oszillatoren berücksichtigt. Laut dem zweiten Newton’schen Gesetz ergibt
sich für die Beschleunigung eines Elektrons:
m~¨r = F~ (t) + F~F (~r) + F~R (~r˙ ).
(4.64)
Hierbei ist FF = −kF ~r die Federkraft der Schwingung, die linear mit der Auslenkung
skaliert, und FR = −mγ~r˙ die Reibungskraft, die proportional zur Geschwindigkeit der
elektronischen Bewegung angenommen werden kann. Somit ergibt sich für die elektronische Bewegung eine einfache Differentialgleichung:
mẍ + mγ ẋ + kF x = −eEo exp (−iωt).
(4.65)
Als Lösungsansatz für Gleichung (4.65) setzen wir harmonische Schwingungen mit der
Frequenz des externen Feldes ein: x(t) = xo exp (−iωt). Um eine etwaige Phasenverschiebung dieser Schwingungen dem externen Feld gegenüber zu berücksichtigen, muss xo als
komplexe Größe betrachtet werden. Für die Auslenkung der Elektronen erhalten wir somit:
1
e
E(t).
(4.66)
x(t) = −
2
m ωo − ω 2 − iγω
Die Auslenkung der Elektronen aus ihren Ruhepositionen führt zu einer Polarisation, die
proportional sowohl zur Elektronendichte N als auch zum Dipolmoment −ex(t) ist:
e2 N
1
E(t).
P~ (t) = −ex(t)N =
2
m ωo − ω 2 − iγω
(4.67)
14
KAPITEL 4. DIE ELEKTROMAGNETISCHE THEORIE DES LICHTS
Für die frequenzabhängige Dielektrizitätskonstante erhalten wir somit7 :
εr (ω) = 1 +
e2 N
1
.
2
εo m ωo − ω 2 − iγω
(4.68)
Bei Medien mit Atomen verschiedener Arten können wir die einzelnen Beiträge zur Dielektrizitätskonstante durch eine Summe berücksichtigen:
εr (ω) = 1 +
Nj
e2 X
.
2
εo m j ωoj − ω 2 − iγj ω
(4.69)
Hierbei ist Nj die entsprechende Dichte der Atome; ωoj und γj die damit verbundene
Resonanzfrequenz sowie die dazugehörige Dämpfung. Unter der Annahme, dass die verschiedenen Resonanzfrequenzen weit auseinander liegen, genügt es, das Verhalten des
Brechunsindex in der Nähe einer einzelnen Resonanz zu betrachten. Im nicht-resonanten
Fall erwarten wir für dünne Medien, dass ε(ω) = 1 + ∆ε mit ∆ε ¿ 1. Für den Brechungsindex können wir dann folgende Näherung einsetzen: n = (1 + δ). Somit erhalten
wir:
(ε − 1) = (n2 − 1) = ((1 + δ)2 − 1) ≈ 2δ.
(4.70)
Wir sehen sofort, dass der Brechungsindex eine komplexe Größe n = nR + inI mit folgendem Real- und Imaginärteil ist:
e2 N
ωo2 − ω 2
2εo m (ωo2 − ω 2 )2 + γ 2 ω 2
γω
e2 N
nI (ω) =
.
2
2εo m (ωo − ω 2 )2 + γ 2 ω 2
nR (ω) = 1 +
(4.71)
(4.72)
Der schematische Verlauf sowohl des Realteils als auch des Imaginärteils des Brechungsindex wird in Abbildung (4.6) dargestellt. Bereiche mit dnR /dω > 0 werden als Bereiche
normaler Dispersion bezeichnet. Der Bereich mit dnR /dω < 0 wird dagegen als Bereich
anormaler Dispersion bezeichnet: nur in diesem Bereich weicht nI signifikant von Null ab,
was zu einer starken Absorption führt. Um die Auswirkung eines komplexen Brechungsindex zu verstehen, müssen wir die Ausbreitung einer ebenen Welle mit entsprechendem
Wellenvektor k = ωn(ω)/c betrachten:
~ t) = E
~ o exp (ikz − iωt) = E
~ o exp (i ωnR z − iωt) exp (− ωnI z).
E(z,
c
c
(4.73)
Die Ausbreitungsgeschwindigkeit und auch die Wellenlänge der ebenen Welle im Medium
werden lediglich durch den Realteil des Brechungsindex bestimmt. Da nI > 0 ist, führt das
zweite exponentielle Glied der Gleichung (4.73) stets zu einer Abnahme der Feldamplitude
mit der Eindringtiefe im Medium. Die Intensität der elektromagnetischen Welle skaliert
mit dem Quadrat der Feldstärke und für die Intensität der Welle gilt:
I(z) = Io exp (−
2ωnI z
) = Io exp (−αz).
c
(4.74)
~ = εr εo E
~ = εo E
~ + P~ . In einem homogenen
Aus der Maxwellgleichungen wissen wir bereits, dass D
~
~
~
~
~
isotropen Medium ist P kE und P = χεo E = (εr − 1)εo E.
7
4.4. DISPERSION UND ABSORPTION VON LICHT
1
0
n
15
n
R
I
w
o
w
Abbildung 4.6: Schematische Darstellung des Real- und Imaginärteils des Brechungsindex.
Hierbei ist Io die Intensität der Welle an der Stelle z = 0 und α der so genannte Extinktionskoeffizient:
e2 N
γω 2
α=
.
(4.75)
εo mc (ωo2 − ω 2 )2 + γ 2 ω 2
Der Imaginärteil des Brechungsindex führt somit zu einer Absorption der Energie der
Welle im Medium. Für ein Medium mit endlicher räumlicher Ausdehnung definieren wir
daher die Transmission durch das Medium:
T =
I(z)
= exp (−αz).
Io
(4.76)
Bisher haben wir in unserer vereinfachten Analyse lediglich dielektrische isolierende Medien betrachtet. Einen interessanten und wichtigen Grenzfall bilden leitende Medien ohne
Rückstellkräfte wie beispielsweise Metalle. Für den Fall einer verschwindenden Federkonstante k → 0 erwarten wir, dass die Resonanzfrequenz ωo auch gegen Null geht. Wenn
auch die Reibungskräfte klein sind,8 lässt sich Gleichung (4.68) entsprechend vereinfachen:
ε(ω) = 1 −
ωp2
e2 N 1
=
1
−
.
εo m ω 2
ω2
(4.77)
In der obigen Gleichung haben wir mit ωp die so genannte Plasmafrequenz eingeführt.
Oberhalb dieser Frequenz kann sich eine elektromagnetische Welle in einem leitenden
Medium ausbreiten. Für Frequenzen unterhalb von ωp ist ε(ω) negativ und reell. Wie
zuvor erhalten wir eine exponentiell abfallende Lösung im Medium, die allerdings mit einer
perfekten Reflektion einer einfallenden Welle verknüpft ist und nicht mit einer Absorption
der einfallenden Energie.
8
Die Reibungskräfte müssen nicht komplett verschwinden. Es genügt, wenn der Limes ωτ À 1 gilt.
Die Ladungsträger führen in diesem Fall mehrere angeregte Schwingungen aus, ohne ein Streuereignis zu
erleiden.