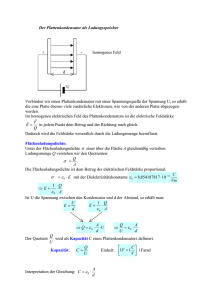
Versuch E1 R0 04

Physikalisch-technisches Messpraktikum: E1
Versuch E1: Elektrisches Feld
Aufgaben:
1. Untersuchen Sie die Abhängigkeit der räumlich konstanten elektrischen Feldstärke im Plattenkondensator von der Spannung und vom Plattenabstand.
2. Untersuchen Sie die Abhängigkeit der Kapazität eines Plattenkondensators von der Plattenfläche, dem Plattenabstand und vom Dielektrikum.
Grundlagen:
•
Für die elektrische Feldstärke E in einem Plattenkondensator gilt der einfache Zusammenhang zur angelegten Spannung U und dem Plattenabstand d:
E=
•
•
•
U
d
Die Feldstärke ist also der Spannung U direkt und dem Plattenabstand d indirekt proportional. Im Innern des Plattenkondensators ist das Feld homogen, d.h. die Feldstärke ist in diesem Bereich räumlich konstant. Die Richtung der elektrischen Feldstärke ist dort überall
gleich von der positiv geladenen zur negativ geladenen Platte gerichtet.
Sie messen die elektrische Feldstärke in einem Plattenkondensator mit einem Elektrofeldmeter. Dabei wird die Kondensatorplatte, an der das Elektrofeldmeter angebracht ist, geerdet. An die gegenüberliegende Platte wird der Pluspol der Spannungsquelle angelegt.
Im ersten Versuchsteil der Aufgabe 1 wird der Zusammenhang zwischen der angelegten
Spannung und der elektrischen Feldstärke untersucht, indem bei konstantem Plattenabstand die Spannung am Kondensator variiert und jeweils die zugehörige elektrische Feldstärke gemessen wird.
Im zweiten Versuchsteil wird die Kondensatorspannung konstant gehalten und die elektrische Feldstärke bei verschiedenen Plattenabständen gemessen.
Die Kapazität C eines Plattenkondensators ist proportional zur Fläche A seiner Platten und
umgekehrt proportional zum Abstand d zwischen den Platten. Sie hängt auch von Stoff zwischen den Platten, dem Dielektrikum ab:
C = ε0 ⋅εr ⋅
•
•
•
A
d
Die relative Dielektrizitätszahl (Permittivitätszahl) εr gibt an, wie vielmal größer die Kapazität eines Kondensators mit Dielektrikum ist als die eines gleichen Kondensators, zwischen
dessen Platten sich Luft oder Vakuum befindet. ε0 ist die Influenzkonstante, die den Wert
8,86*10-12 F/m hat.
Die Kapazitäten verschiedener Kondensatoren werden bestimmt, indem ihre Platten mit
einer bestimmten Spannung aufgeladen und jeweils die aufgebrachten Ladungen mit einem
Gleichstrommessverstärker gemessen werden. Die Quotienten C = Q/U werden berechnet.
Im ersten Versuchsteil der Aufgabe 2 werden 2 Plattenkondensatoren mit verschiedenen
Plattenflächen und gleichen –abständen untersucht und ihre Kapazitäten verglichen.
Im zweiten Versuchsteil ist der Abstand zwischen den Platten zu variieren und bei fest gehaltener Spannung über die Messung der Ladung die jeweilige Kapazität zu bestimmen.
Im dritten Versuchsteil wird für eine Spannung und einen Abstand der Platten die Kapazität
des Kondensators einmal ohne Dielektrikum und einmal mit Dielektrikum bestimmt und
die relative Dielektrizitätszahl berechnet.
-1-
Physikalisch-technisches Messpraktikum: E1
•
In der Umgebung eines geladenen kugelförmigen Konduktors existiert ein elektrisches Feld.
Dabei sind die elektrische Feldstärke E in einem beliebigen, aber festen Punkt und die Ladung Q auf der Kugel einander proportional. Die Stärke des elektrischen Feldes E hängt
außerdem vom Abstand r zwischen dem Kugelmittelpunkt und dem Messpunkt ab. Die
Feldstärke E nimmt quadratisch mit dem Abstand r ab. Befindet sich die Kugel im Vakuum
(oder auch näherungsweise in Luft) berechnet sich der Betrag der elektrischen Feldstärke
um eine Punktladung (oder kugelsymmetrische Ladungsverteilung wie die Kugel) folgendermaßen:
E=
Q
4π ε 0 ⋅ r 2
In der Umgebung der geladenen Kugel ist das elektrische Feld in jedem Messpunkt entweder genau in Richtung des Kugelmittelpunktes gerichtet (negativ geladene Kugel) oder vom
Mittelpunkt der Kugel weggerichtet (positiv geladene Kugel).
Literatur:
Dobrinski, Physik für Ingenieure:
3.1.2 Elektrisches Feld
Geschke, Physikalisches Praktikum: Elektrizitätslehre
2.0.1 Elektrisches Feld
2.1
Elektrostatische Felder
Grimsehl, Lehrbuch der Physik – Band 2:
2
Das statische elektrische Feld
Hering, Physik für Ingenieure:
4.3
Elektrisches Feld
Stroppe, Physik:
23
Das elektrostatische Feld
u.v.a.m.!
Testfragen:
1. Erläutern Sie die Definition der elektrischen Feldstärke! Welche Aussagen für den Vektor
der elektrischen Feldstärke kann man aus einem Feldlinienbild ableiten?
2. Wie ist das elektrische Feld im Plattenkondensator und um eine Kugelladung beschaffen? Skizzieren Sie! Von welchen Größen hängt die Stärke des Feldes im Raum außerhalb der Ladungen in beiden Anordnungen ab?
3. Wie ist die Kapazität einer Leiteranordnung allgemein definiert? Wie hängt die Kapazität
eines Plattenkondensators von seiner Geometrie und dem Medium zwischen den Platten
ab?
-2-
Physikalisch-technisches Messpraktikum: E1
Hinweise zur experimentellen Durchführung:
Machen Sie sich zu Beginn des Versuches mit den Betriebsanleitungen zum Elektrofeldmeter
(EFM), dem Gleichstrommessverstärker, dem Hochspannungsgerät, dem Geregelten Netzgerät
und dem Netzgerät, universal vertraut (beachten Sie insbesondere die angestrichenen Absätze
in den Betriebsanleitungen!).
Zu 1:
Abbildung 1: Versuchsaufbau zur Aufgabe 1
Abb. 1 zeigt den Versuchsaufbau. Stativstange und Klemmsäule (für das Elektrofeldmeter - EFM)
werden in die Tonnenfüße gesteckt und verschiebbar auf den Maßstab gestellt. Schrauben Sie
die Kondensatorplatte mit der Bohrung an das EFM (die Schrauben müssen leichtgängig gehen,
sonst zerstören Sie das EFM!) und befestigen das EFM in der Klemmsäule. Die zweite Kondensatorplatte wird mit dem angeschraubten Plexiglasstiel und einer Doppelmuffe auf gleicher Höhe,
wie die erste Platte, an der Stativstange befestigt.
Verbinden Sie die Kondensatorplatte mit dem Pluspol des Ausgangs 0... 300 V am geregelten
Netzgerät. Verbinden Sie Minuspol und Erdbuchse des Netzgerätes. Schließen Sie diesen Ausgang des Netzgerätes an das erste Multimeter (Gleichspannung – 200 V) an. Verbinden Sie den
Ausgang des Netzgerätes (universal) polrichtig mit dem Eingang des EFM. Schließen Sie den
Ausgang des EFM an das zweite Multimeter (Gleichspannung – 20 V). Verbinden Sie die Stativstange des EFM (damit auch die zweite Kondensatorplatte) mit der Erdbuchse am Netzgerät.
Lassen Sie an dieser Stelle ihre Schaltung vom Assistenten überprüfen, bevor Sie die Geräte
einschalten!
Aufgabenteil a):
Stellen Sie zwischen den Kondensatorplatten einen Abstand von 3 cm ein. Überprüfen Sie die
Parallelität der Platten nochmals. Berühren Sie ab sofort die spannungsführenden Teile nicht
mehr! Stellen Sie den Gleichspannungsausgang des Netzgerätes (universal) auf ca. 16 V ein.
-3-
Physikalisch-technisches Messpraktikum: E1
Schalten Sie das EFM ein (Spannungszufuhr einschalten) und justieren den Nullpunkt des
EFM (s. auch Betriebsanleitung). Schalten das EFM auf den Messbereich 10 kV/m um.
Kommen Sie möglichst während des Justierens und auch während des Messens nicht mehr
in die Nähe des Kondensators, um die Messungen nicht zu verfälschen!
Schalten Sie die Spannung am Kondensator ein. Beginnen Sie mit 40 V. Tragen Sie die Kondensatorspannung und die abgelesene Spannung am EFM und die dazugehörige Feldstärke
(10 V entspricht einer elektrischen Feldstärke von 10 kV/m) in eine Tabelle ein.
Erhöhen Sie die Spannung schrittweise um 40 V bis zu einer Maximalspannung von 280 V.
Achten Sie auf die Wahl des richtigen Messbereiches beim Multimeter!
Schalten Sie die Spannungsversorgung des Plattenkondensators aber nicht die des EFM wieder aus.
Aufgabenteil b):
Gehen Sie wie im Versuchsteil a) vor. Beginnen Sie mit einem Plattenabstand von 1 cm.
Stellen Sie jetzt eine Kondensatorspannung von 95 V ein. Nehmen Sie die gleichen Werte,
wie bei a) auf. Halten Sie jetzt die Kondensatorspannung konstant und ändern den Plattenabstand in Schritten von 1 cm bis maximal 10 cm.
Schalten Sie die Spannungsversorgung des Plattenkondensators und des EFM wieder aus.
Zu 2:
Abbildung 2: Versuchsaufbau zur Aufgabe 2
Abbildung 2 zeigt den Versuchsaufbau zur 2. Aufgabe. Je eine Platte des großen (800 cm²) und
des kleinen (400 cm²) Kondensators wird mit Hilfe eines Isolierstiels so am Dreifuß befestigt,
dass die Platten horizontal stehen. Auf diesen Platten werden je 3 - 4 der 10 mm hohen Abstandsplättchen (Pinzette verwenden!) und darauf die passenden Kondensatorplatten gelegt.
Die 2 Konduktorkugeln werden auf die Isolierstiele gesteckt und in den Tonnenfüßen befestigt.
Eine Konduktorkugel wird mittels der Hochspannungsleitung und dem 10 MΩ
Ω - Widerstand an
der oberen Buchse des Hochspannungsgerätes angeschlossen. Die unteren beiden Platten der
Kondensatoren werden mit der unteren Buchse und diese mit der Erdungsbuchse des Hochspannungsgerätes verbunden. Die zweite Konduktorkugel wird über das BNC-Kabel und den
Adapter an den Ladungseingang des Gleichstrommessverstärkers angeschlossen. Den Ausgang
des Verstärkers schließen Sie an ein Multimeter (Gleichspannung – 20V) an.
Lassen Sie an dieser Stelle wieder ihre Schaltung vom Assistenten überprüfen, bevor Sie die
Geräte einschalten!
-4-
Physikalisch-technisches Messpraktikum: E1
Schalten Sie zuerst den Messverstärker ein. Gehen Sie auf Ladungsmessung und den Bereich
100 nAs (Damit entspricht eine am Ausgang des Verstärkers gemessene Spannung von 10 V
genau einer Ladungsmenge von 100 nAs! Überschreitet die angezeigte Spannung während der
Messreihe 10 V, ist auf 1000 nAs zu wechseln, womit dann 10 V genau 1000 nAs entspricht).
Entladen Sie zuerst die Konduktorkugel. Sollte das Multimeter nicht 0 V anzeigen, justieren Sie
den Verstärker, indem Sie bei gedrücktem Entladeknopf die Nullpunktskorrektur solange betätigen, bis am Multimeter 0 V angezeigt werden.
Aufgabenteil a):
Schalten Sie eine Hochspannung von 1 kV ein. Berühren Sie mit der Hochspannungskonduktorkugel kurzzeitig die obere Platte des großen Kondensators. Bringen Sie die zweite Kugel
kurzzeitig mit der oberen Platte des großen Kondensators in Verbindung und messen mit
dem Multimeter die der Platte entnommene Ladung (entsprechend der abgelesenen Spannung an Multimeter). Achtung, bringen Sie nie beide Kugeln direkt miteinander in Kontakt!
Entladen Sie die zweite Kugel (Entladeknopf drücken) und korrigieren bei Bedarf die Nullpunktseinstellung. Nach ca. 1 min wiederholen Sie das Gleiche mit dem kleinen Kondensator.
Schalten Sie das Hochspannungsgerät aus.
Aufgabenteil b):
Bauen Sie den kleinen Kondensator wieder ab.
Im folgenden wird der große Plattenkondensator bei einer konstanten Spannung von 400 V
verwendet und bei verschiedenen Plattenabständen die auf der oberen Platte befindliche Ladungsmenge gemessen. (Berühren Sie die Hochspannungskonduktorkugel nicht!)
Stellen Sie dazu folgende Abstände ein: 3 mm, 6 mm, 9 mm, 12 mm, 18 mm, 24 mm und
30 mm. Verwenden Sie dazu die 10 mm, die 4 mm (gelb), die 3 mm (blau) und 2 mm (rot)
Abstandsplättchen (Pinzette verwenden!).
Vergessen Sie nicht, vor jeder Messung die Messkugel durch Drücken des Entladeknopfes
wieder zu entladen und bei Bedarf nachzujustieren!
Schalten Sie das Hochspannungsgerät aus.
Aufgabenteil c):
Machen Sie mit dem großen Plattenkondensator bei ca. 400 V und einem Abstand von 10
mm 2 Messungen: einmal mit dem „Dielektrikum“ Luft (Verwendung der Abstandsplättchen) und zum anderen mit der Kunststoffplatte. Messen Sie jeweils die aufgebrachte Ladung.
Vergessen Sie nicht, zwischendurch die Messkugel durch Drücken des Entladeknopfes wieder
zu entladen und bei Bedarf nachzujustieren!
Schalten Sie das Hochspannungsgerät aus, und entladen beide Kugeln und die Platten, bevor
Sie den Verstärker ausschalten.
Hinweise zur Auswertung der Messergebnisse:
Zu 1:
Stellen Sie für den Aufgabenteil a) die elektrische Feldstärke über der Kondensatorspannung
graphisch dar. Ermitteln Sie den Anstieg der Regressionsgeraden. Vergleichen Sie den Anstieg
mit dem zu erwartenden Wert und diskutieren eventuelle Unterschiede. Diskutieren Sie Abweichungen ihrer Messpunkte von der Regressionsgeraden.
Stellen Sie im Aufgabenteil b) die elektrische Feldstärke über dem Plattenabstand dar. Legen
Sie über die Messpunkte die passende Regressionskurve und vergleichen Sie wiederum die
durch Anpassung ermittelten Werte der Regressionskurve mit ihren Erwartungen. Alternativ
dazu können Sie auch die Feldstärke über der Größe: 1/Plattenabstand darstellen und eine Regressionsgerade an die Messpunkte anpassen. Diskutieren Sie Ihr Ergebnis analog zu a).
-5-
Physikalisch-technisches Messpraktikum: E1
Zu 2:
Stellen Sie für den Aufgabenteil a) in einer Tabelle die Plattengröße - der gemessenen Ladung,
der von Ihnen zu berechnenden Kapazität (aus der gemessenen Ladung und der angelegten
Spannung) und dem Quotienten aus der Kapazität und der Kondensatorfläche gegenüber. Geben Sie Ursachen für eventuell vorhandene Unterschiede der beiden Quotienten an.
Geben Sie für die Aufgabenteil b) neben dem Plattenabstand die gemessene Ladung, den inversen Plattenabstand und die berechnete Kapazität (wie bei Teilaufgabe a) in einer Tabelle an.
Stellen Sie graphisch die Kapazität als Funktion des Abstandes oder als Funktion von 1/Abstand dar. Führen Sie entsprechend eine sinnvolle Funktionsanpassung durch. Geben Sie Gründe für Abweichungen von Messpunkten von der Regressionskurve an. Vergleichen Sie die Parameter der angepassten Kurve mit ihren Erwartungen.
Berechnen Sie für den Aufgabenteil c) die beiden Kapazitäten (wie bei Teilaufgabe a) und ermitteln aus dem Verhältnis dieser Kapazitäten die relative Dielektrizitätszahl εr der Kunststoffplatte.
Versuchszubehör:
2 Dreifüße, 4 Tonnenfüße, Doppelmuffe, Stativstange, Klemmsäule, 1m Maßstab
2 Isolierstiele mit je einer Konduktorkugeln (40 mm Durchmesser)
Netzgerät (universal), geregeltes Netzgerät, Hochspannungsgerät, 2 Multimeter
2 Kondensatorplatten 283 mm x 283 mm, Kondensatorplatte mit Bohrung
2 Kondensatorplatten 200 mm x 200 mm
Abstandsplättchen 10 mm, 4 mm, 3 mm und 2 mm; Pinzette
Kunststoffplatte 283 mm x 283 mm
Elektrofeldmeter mit Zubehör
Gleichstrommessverstärker
Verbindungsleitungen: 50 cm (4x rot, 3x blau, 1x grüngelb), 10 cm (1x blau, 1x grüngelb)
Verbindungsleitung 30 kV mit Widerstand 10 MΩ
Abgeschirmtes BNC-Kabel mit Adapter zu 4-mm-Stecker
Nordhausen, d. 01.03.11
-6-