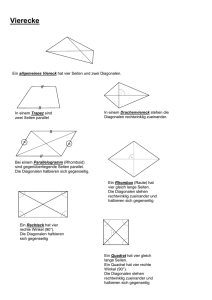
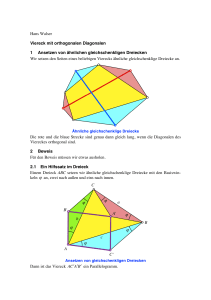
Beweise mit Vektoren

Datum:
Arbeitsblatt
Beweise mit Vektoren
Aufgabe 1:
Beweisen Sie: Ist ein Viereck ABCD ein Parallelogramm, so halbieren sich die Diagonalen.
Beweis: (s. auch LS S. 244 Beispiel 1)
Vorgehensweise
Beweis der Aufgabe
1. Schritt:
D
C
M
Skizze
A
2. Schritt:
Benenne wichtige Vektoren,
so wenige wie möglich.
B
−→
−−→
Benennungen: ~u = AB; ~v = AD
D
C
M
v
A
3. Schritt:
Drücke die Voraussetzungen
aus.
4. Schritt:
Drücke die Behauptung aus.
5. Schritt:
Folgere aus der Voraussetzung die Behauptung.
Suche einen geschlossenen
Vektorzug.
u
B
−→ −−→
Voraussetzungen: Die Seiten sind parallel, d.h. AB = DC = ~u;
−−→ −−→
AD = BC = ~v .
Behauptung: Die Diagonalen werden von ihrem Schnittpunkt
−→
−−→ −−→
−−→
−−→ −−→
halbiert: AM = M C = 12 AC und DM = M B = 21 DB
−→
−−→
AC = ~u + ~v ; DB = ~u − ~v ;
−→
−−→
Für bisher unbekannte reelle Zahlen m,n gilt: AM = m · AC und
−−→
−−→
M B = n · DB
−−→ −−→ −→
AM + M B + BA = ~o
Setze ein:
m · (~u + ~v ) + n · (~u − ~v ) + (−~u) = ~o
Klammere um:
(m + n − 1) · ~u + (m − n) · ~v = ~o
Weil ~u und ~v linear unabhängig sind, gilt
m + n − 1 = 0 und m − n = 0
Lösen des LGS liefert m = n = 12 .
Damit ist die Behauptung bewiesen.
Aufgabe 2:
Beweisen Sie die Umkehrung des Satzes:
Halbieren sich in einem Viereck ABCD die Diagonalen, so ist das Viereck ein Parallelogramm.