Wir behandeln im Folgenden nur gerade Pyramiden und Kegel

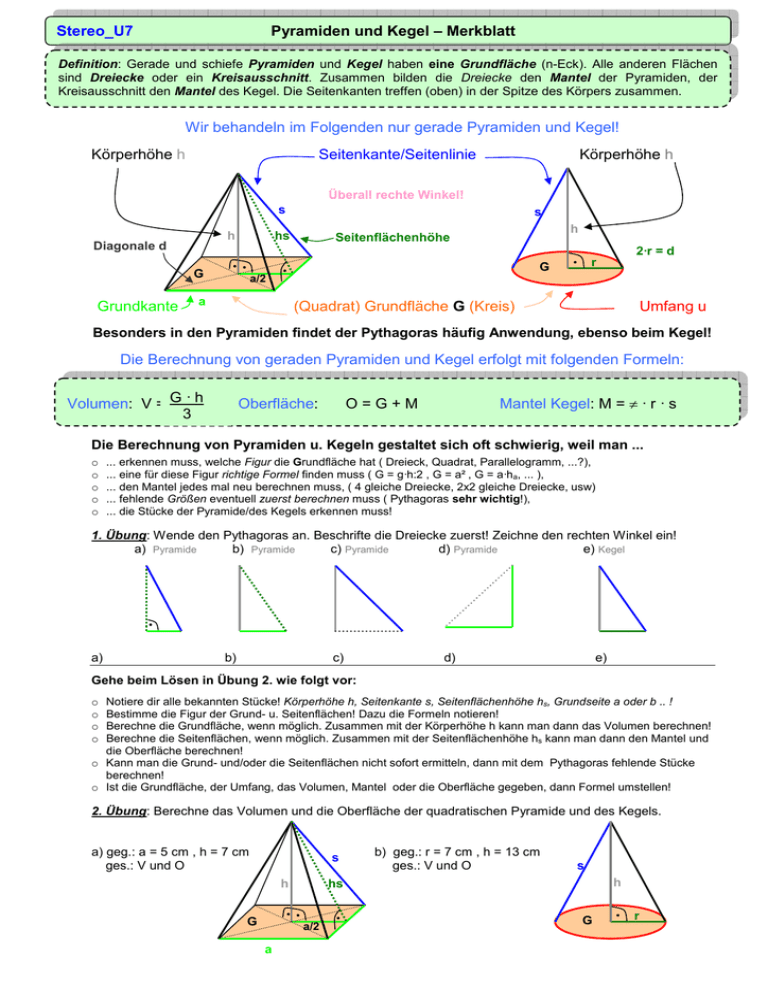
Stereo_U7
Pyramiden und Kegel – Merkblatt
Definition: Gerade und schiefe Pyramiden und Kegel haben eine Grundfläche (n-Eck). Alle anderen Flächen
sind Dreiecke oder ein Kreisausschnitt. Zusammen bilden die Dreiecke den Mantel der Pyramiden, der
Kreisausschnitt den Mantel des Kegel. Die Seitenkanten treffen (oben) in der Spitze des Körpers zusammen.
Wir behandeln im Folgenden nur gerade Pyramiden und Kegel!
Körperhöhe h
Seitenkante/Seitenlinie
Körperhöhe h
Überall rechte Winkel!
s
h
Diagonale d
hs
h
Seitenflächenhöhe
2·r = d
G
Grundkante
s
● ●
G
●
r
●
a/2
a
(Quadrat) Grundfläche G (Kreis)
Umfang u
Besonders in den Pyramiden findet der Pythagoras häufig Anwendung, ebenso beim Kegel!
Die Berechnung von geraden Pyramiden und Kegel erfolgt mit folgenden Formeln:
Volumen: V = G · h
3
Oberfläche:
Mantel Kegel: M = π · r · s
O=G+M
Die Berechnung von Pyramiden u. Kegeln gestaltet sich oft schwierig, weil man ...
o
o
o
o
o
... erkennen muss, welche Figur die Grundfläche hat ( Dreieck, Quadrat, Parallelogramm, ...?),
... eine für diese Figur richtige Formel finden muss ( G = g·h:2 , G = a² , G = a·ha, ... ),
... den Mantel jedes mal neu berechnen muss, ( 4 gleiche Dreiecke, 2x2 gleiche Dreiecke, usw)
... fehlende Größen eventuell zuerst berechnen muss ( Pythagoras sehr wichtig!),
... die Stücke der Pyramide/des Kegels erkennen muss!
1. Übung: Wende den Pythagoras an. Beschrifte die Dreiecke zuerst! Zeichne den rechten Winkel ein!
a) Pyramide
b) Pyramide
c) Pyramide
d) Pyramide
e) Kegel
●
a)
b)
c)
d)
e)
Gehe beim Lösen in Übung 2. wie folgt vor:
Notiere dir alle bekannten Stücke! Körperhöhe h, Seitenkante s, Seitenflächenhöhe hs, Grundseite a oder b .. !
Bestimme die Figur der Grund- u. Seitenflächen! Dazu die Formeln notieren!
Berechne die Grundfläche, wenn möglich. Zusammen mit der Körperhöhe h kann man dann das Volumen berechnen!
Berechne die Seitenflächen, wenn möglich. Zusammen mit der Seitenflächenhöhe hs kann man dann den Mantel und
die Oberfläche berechnen!
o Kann man die Grund- und/oder die Seitenflächen nicht sofort ermitteln, dann mit dem Pythagoras fehlende Stücke
berechnen!
o Ist die Grundfläche, der Umfang, das Volumen, Mantel oder die Oberfläche gegeben, dann Formel umstellen!
o
o
o
o
2. Übung: Berechne das Volumen und die Oberfläche der quadratischen Pyramide und des Kegels.
a) geg.: a = 5 cm , h = 7 cm
ges.: V und O
s
h
●
a/2
a
s
h
hs
● ●
G
b) geg.: r = 7 cm , h = 13 cm
ges.: V und O
G
●
r
Lösungen:
1. Übung: Wende den Pythagoras an. Beschrifte die Dreiecke zuerst! Zeichne den rechten Winkel ein!
a) Pyramide
b) Pyramide
c) Pyramide
d) Pyramide
e) Kegel
●
a) s² = (a/2)² + hs²
b) hs² = h² + (a/2)² c) s² = h² + (d/2)²
d) d² = a² + a²
e) s² = h² + r²
2. Übung:
a) quadratische Pyramide!
geg.: a = 5 cm , h = 7 cm (Körperhöhe)
ges.: V und O
G = a² = (5 cm)² = 25 cm²
u = 4 · a = 4 · 5 cm= 20 cm
Mantel = 4 gleich große Seitenflächen (Dreiecke) Grundseite ist a , Höhe-Dreieck ist hs !!
hs mit dem Pythagoras errechnen (siehe oben)!
hs² = h² + (a/2)²
hs =
M=
4⋅
V=
G·h
3
a⋅ hs
2
=
=
2 ⋅ a ⋅ hs
25 cm² · 7 cm
3
(7cm)² + (2,5cm)² = 7,433034374 cm ~7,43 cm
= 2 · 5 cm · 7,433034374 cm = 74,33034373 cm² ~ 74,33 cm²
= 58,33 cm³
O = G + M = 25 cm² + 74,33034373 cm² = 99, 33034373 cm²
Es geht auch kürzer: weiter unten!
Die gesehene ist eine von mehreren möglichen Lösungswegen!!
V=
G·h
3
O=G+M
V=
a² · h
3
O = a² + 2 · a · hs
V=
25 cm² · 7 cm
3
O = (5cm)² + 2 · 5 cm · 7,433034374 cm
V = 58,33 cm³
b) Kegel!
O = 99, 33034373 cm²
Mantelfläche Kegel! M = π·r·s
G = π·r² = 153,93804 cm²
u = 2·π·r = 43,98229715 cm
s mit dem Pythagoras errechnen (siehe oben)!
s² = h² + r²
s =
(13cm)² + (7cm)² = 14,76482306 cm ~14,76 cm
M = π·r·s = 324,6954176 cm²
V = 667,0648401 cm²
O = 478,6334576 cm²