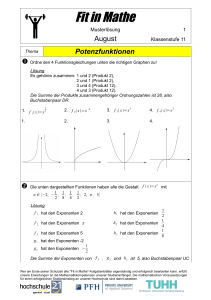
Potenzrechnung

U. Rausch, 2010
Potenzrechnung
1
Potenzrechnung
1
Schreibweise und Potenzrechenregeln
Unter einer Potenz versteht man ein Symbol der Form
ax ,
gesprochen a hoch x“, wobei a und x (reelle) Zahlen sind. Dabei nennt man a die Basis oder
”
Grundzahl und x den Exponenten oder die Hochzahl der Potenz.
Es gelten die Potenzrechenregeln
(P1)
ax · ay = ax+y
(P2)
(ax )y = ax·y
(P3)
ax · bx = (ab)x
Bisher wurde weder gesagt, wie eine Potenz definiert ist, noch, welche Voraussetzungen zu beachten sind und warum die Potenzrechenregeln gelten. Dies wird gleich nachgeholt werden. Es
hängt entscheidend von der Beschaffenheit des Exponenten ab:
Für natürliche Zahlen als Exponenten ist die Potenz einfach eine abgekürzte Schreibweise für
ein Produkt von lauter gleichen Faktoren. Die Gültigkeit der Potenzrechenregeln ist in diesem
Fall leicht festzustellen.
Anschließend wird die Definition von ax in mehreren Schritten auf immer umfangreichere Zahlbereiche für x erweitert. Dabei werden zwei Prinzipien beachtet:
. Bei jedem Schritt muß die neue“ Definition die alte“ umfassen; das heißt, was zuvor
”
”
definiert wurde, darf nicht mehr verändert werden.
. Die Potenzrechenregeln sollen ihre Gültigkeit behalten.
Wir werden sehen, daß dadurch alles weitere schon im wesentlichen festgelegt ist.
2
Natürliche Exponenten
Ist der Exponent eine natürliche Zahl n, so ist an definiert als Produkt von n Faktoren, die alle
gleich a sind:
an := |a · a ·{za · · · a}
(n ∈ N),
n Faktoren
1
2
3
also a := a, a := a · a, a := a · a · a und so weiter.
Die Potenzrechenregeln lassen sich dann leicht bestätigen (m, n ∈ N):
(P1):
am · an = |a · a ·{za · · · a} · |a · a ·{za · · · a} = |a · a ·{za · · · a} = am+n .
m Faktoren
n Faktoren
m+n Faktoren
(P2) ergibt sich am schnellsten durch mehrfache Anwendung von (P1):
z
n Summanden
}|
{
(am )n = |am · am {z
· am · · · am} = a m+m+m+...+m = am·n .
n Faktoren
(P3) erhält man, indem man die Faktoren passend anordnet:
an · bn = |a · a ·{za · · · a} · |b · b ·{zb · · · b} = (ab) · (ab) · (ab) · · · (ab) = (ab)n .
|
{z
}
n Faktoren
Beispiel 1)
25 = 32 ,
n Faktoren
(−3)3 = −27,
³ 1 ´2
5
n Faktoren
1
=
.
25
U. Rausch, 2010
3
3.1
Potenzrechnung
2
Ganzzahlige Exponenten
Der Exponent Null
Wie soll a0 definiert werden? Wenn die Regel (P1) weiter gültig bleiben soll, dann folgt
a = a1 = a1+0 = a1 · a0 = a · a0 ,
und wenn a 6= 0 ist, dann ergibt Division der Gleichung a = a · a0 durch a, daß
a0 := 1
gesetzt werden muß. Im Fall a = 0 ist dieser Schluß nicht zulässig, aber man setzt auch dann
00 := 1.
Für diese Festsetzung spricht einfach, daß sie sich in vielen Situationen als praktisch erweist,
indem sie einem die Behandlung von Sonderfällen erspart.
3.2
Negative ganze Exponenten
Es sei n ∈ N; wir betrachten den Exponenten x = −n , eine negative ganze Zahl.
Aufgrund von (P1) folgt
an · a−n = an−n = a0 = 1.
Hieraus ersieht man zunächst, daß, damit diese Gleichung überhaupt erfüllbar ist, an 6= 0, d.h.
a 6= 0 sein muß, und dann, daß
1
a−n = n
(a 6= 0)
a
gelten muß. Insbesondere ist a−1 der Kehrwert a1 von a.
³ 1 ´−2
1
1
, (−3)−3 = − ,
= 25.
Beispiel 2) 2−5 =
32
27
5
3.3
Anmerkung
Wir haben nun gesehen, wie man Potenzen mit ganzzahligen Exponenten definieren muß , wenn
die Potenzrechenregeln weiterhin gelten sollen.
Eigentlich müßten wir jetzt anschließend auch beweisen, daß mit diesen Definitionen alle drei
Potenzrechenregeln für alle möglichen Kombinationen ganzzahliger Exponenten tatsächlich gelten. Das ist nicht schwer, aber ein bißchen mühsam (und langweilig); deshalb verzichten wir hier
darauf. Im folgenden Abschnitt werden wir ebenso verfahren.
4
Rationale Exponenten
Als nächstes betrachten wir als Exponenten rationale Zahlen, also Brüche der Form
x =
m
n
Wir beginnen mit dem einfachsten Fall:
mit m ∈ Z, n ∈ N.
U. Rausch, 2010
4.1
Potenzrechnung
3
Stammbrüche
(So nennt man Brüche der Form
Wir setzen zur Abkürzung u :=
1
1/n zu
n mit n ∈ N.) Wie ist a
a1/n ; dann ergibt die Regel (P2):
definieren?
un = (a1/n )n = a(1/n)·n = a1 = a .
u muß also eine Lösung der Gleichung un = a , d.h., eine n-te Wurzel aus a sein.
Bezüglich der Lösungen der Gleichung un = a muß man unterscheiden, ob n eine gerade oder
ungerade Zahl ist:
. Ist n ungerade, so besitzt die Gleichung un = a für jedes a ∈ R genau eine reelle Lösung;
√
diese bezeichnet man mit dem Symbol n a .
. Ist n gerade, so gibt es drei Möglichkeiten:
– Im Fall a < 0 besitzt die Gleichung un = a keine reelle Lösung.
– Die Gleichung un = 0 besitzt nur die Lösung u = 0; man setzt
√
n
0 := 0.
– Im Fall a > 0 besitzt die Gleichung un = a genau zwei reelle Lösungen; diese
unterscheiden sich nur durch das Vorzeichen.
√
Mit dem Symbol n a bezeichnet man die positive Lösung.
Man definiert
a1/n :=
√
n
a,
wobei man also im Fall, daß n gerade ist, a ≥ 0 voraussetzen muß.
³ 1 ´1/4 1
Beispiel 3) 41/2 = 2, (−8)1/3 = −2,
= .
16
2
4.2
Beliebige Brüche
Für x = m/n mit m ∈ Z , n ∈ N ergibt sich mit (P2) einerseits:
ax = am/n = am·(1/n) = (am )1/n =
und andererseits
√
n m
a
√
ax = am/n = a(1/n)·m = (a1/n )m = ( n a )m .
Wenn alles mit rechten Dingen zugeht, sollten diese beiden Ausdrücke gleich sein. Wenn a positiv
(oder, im Fall m ≥ 0 , auch = 0) ist, sind sie tatsächlich gleich, aber
Vorsicht!
Für rationale Exponenten gelten die Potenzrechenregeln nur dann uneingeschränkt,
wenn alle vorkommenden Basen positiv sind.
Mit negativen Basen kommt man nämlich in Schwierigkeiten der folgenden Art:
p
√
. Wegen 1 = 22 sollte −3 = (−3)1 = (−3)2/2 =
(−3)2 = ( −3 )2 sein.
p
√
√
Aber
(−3)2 = 9 = +3, und ( −3 )2 ist gar nicht definiert.
p
√
√
. Wegen 13 = 26 sollte −2 = 3 −8 = (−8)1/3 = (−8)2/6 = 6 (−8)2 = ( 6 −8 )2 sein.
p
√
√
Aber 6 (−8)2 = 6 64 = +2, und ( 6 −8 )2 ist gar nicht definiert.
Beispiel 4)
43/2 = (41/2 )3 = 23 = 8,
³ 1 ´−3/4
= 16 3/4 = (24 ) 3/4 = 23 = 8.
16
U. Rausch, 2010
5
Potenzrechnung
4
Reelle Exponenten
Um ax für eine beliebige reelle Zahl x definieren zu können, muß man von vornherein a > 0
voraussetzen. Die Definition selber erfordert – das liegt in der Natur der Sache – die Bildung
von Grenzwerten und sprengt damit den Rahmen dieses Kurses. Es sei nur angedeutet, daß sie
auf den folgenden zwei Prinzipien beruht:
1. Jede reelle Zahl x läßt sich beliebig genau durch rationale Zahlen r annähern.
2. ar wird eine beliebig genaue Näherung für ax , sobald nur r nahe genug bei x liegt.
(Man sagt auch: ax hängt stetig vom Exponenten x ab.)
Die Gültigkeit der Potenzrechenregeln überträgt sich dabei von den rationalen auf die reellen
Exponenten.
6
Potenz- und Exponentialfunktionen
Hält man x fest und betrachtet a als variabel, so bezeichnet man die so erklärte Funktion
f (a) := ax
als Potenzfunktion. Aufgrund der obigen Überlegungen ist sie, je nachdem zu welchem Zahlenbereich x gehört, definiert für alle a ∈ R, für a 6= 0, für a ≥ 0 oder nur für a > 0 .
Nimmt man dagegen a > 0 als fest an und betrachtet ax in Abhängigkeit vom Exponenten x,
g(x) := ax ,
so spricht man von einer (allgemeinen) Exponentialfunktion. Sie ist für alle reellen x definiert.
7
7.1
Ergänzende Bemerkungen
Klammerersparnisregeln
Um Klammern zu sparen, verabredet man, daß die Potenzierung eine höhere Priorität hat als
Addition und Multiplikation, also vor diesen ausgewertet wird. Das heißt:
. a + bn bedeutet a + (bn ); ist dagegen (a + b)n gemeint, müssen Klammern gesetzt werden.
. abn bedeutet a · (bn ); ist dagegen (ab)n gemeint, müssen Klammern gesetzt werden.
Beispiel 5) 2 + 3 · 52 = 77 .
Bei geschachtelten“ Potenzen wird immer die oberste“ zuerst ausgewertet, also z.B.:
”
”
3
3
33 bedeutet 3(3 ) = 327 ; wenn dagegen (33 )3 = 39 gemeint ist, müssen Klammern gesetzt
werden.
7.2
Alternierende Vorzeichen
Abwechselnde ( alternierende“) Vorzeichen lassen sich bequem durch den Ausdruck
”
(−1)n
mit n ∈ Z
codieren; es gilt nämlich
½
n
(−1)
=
+1, wenn n gerade ist,
−1, wenn n ungerade ist.
U. Rausch, 2010
8
Potenzrechnung
5
Aufgaben
1. Schreiben Sie als Potenzen
(a) (−a−1 ) · (−a−1 ) · (−a−1 ) ;
(b) −(b − a) · (a − b) · (a − b) .
2. Fassen Sie zusammen
(a) 12a2 b − 6ab2 − 15a2 b + 6ab2 − 7a2 b ;
(b) 4(a − b)2 + 2(b − a)2 − 3(a − b)2 .
3. Vereinfachen Sie die folgenden Ausdrücke:
³ 1 ´−4
³
1 ´−5
(a) 4−2 ·
;
(b)
− −4
;
4
a
4. Vereinfachen Sie:
3an+1 · 6xn+7 · 9bx+1
(a)
;
3xn · 2bx+1 · 3a
18xa+4 4x7−3a
(c)
:
;
2y 5a+7 9y 8+5a
(e)
(c)
³ 3 ´−2 ³ 4 ´−3
·
.
4
3
ax+1 · bx+3 · a3x−1 · bx+3
;
ax−2 · b3−x · ax · bx+1
42a2 b3 · xn+1 70a3 b2 · xn+2
(d)
:
;
36c3 · y 2 · z n−3 54c2 y 4 · z n−2
(b)
27x−5 · y −6 · z −1 49x−2 · y −3 · z −4
·
.
45x−4 · y −5 · z 0 42x−3 · y −4 · z −3
5. Vereinfachen Sie:
µ 2 2 ¶5 µ 2 ¶5
ab c
a bc
:
;
(a)
2
de f
d2 ef
(b)
(rs + rt)m+3 um+1
.
(rsu + rut)m−2