Supraleitung und Suprafluidität

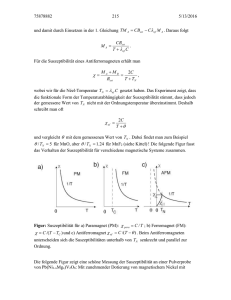
Supraleiter erster Art
228
Nb substituiertes SrTiO3, und Ba(Pb1 xBix)O3,
letzteres mit einem Tc-Wert von 11 K. In der
Verbindung BaBiO3 (x ˆ 1) konnte durch die
partielle Substitution des Ba durch Kalium der
Tc-Wert mehr als verdoppelt werden. Weitere
supraleitende Oxide sind die Wolframbronzen
AxWO3 (mit A ˆ Na, K, Rb, Cs; tetragonal verzerrte Perowskit-Struktur oder in der hexagonalen Modifikation) und der % Spinell LixTi3 xO4, mit 0,8 x 1,33.
Die höchsten Tc-Werte der Hauptgruppenverbindungen wurden für die Alkaliderivate des
% Fullerens gefunden, einer andere Klasse von
Hochtemperatursupraleitern. Demgegenüber
weisen die Alkaliderivate des % Graphits KC8,
RbC8, und CsC8 Sprungpunkte von etwa
500 mK, 100 mK bzw. 20 mK auf. Erwähnt sei
noch das einzige supraleitende, anorganische
% Polymer, (SN)x und dessen Bromderivat (Tc 0,3 K)
Nur wenige Systeme haben bisher technische
Anwendungen gefunden, z.B. Nb (% SQUIDs),
NbTi und Nb3Sn beim Bau von supraleitenden
Hochfeldmagneten (z.B. für % Beschleuniger und
% Kernspintomographie) und jüngst die % Hochtemperatur-Supraleiter, v.a. Y-123.
[AL1]
Supraleiter erster Art, % Supraleiter mit positiver Oberflächenenergie zwischen supra- und
normalleitender Phase (% Supraleitung). Sie
zeigen den % Meiûner-Ochsenfeld-Effekt. Bei
Überschreiten des kritischen Feldes Hc gehen sie
sprunghaft in den Normalzustand über, falls die
Probengeometrie einen verschwindenden Entmagnetisierungsfaktor n aufweist. Für Proben
mit n > 0 wird der Zwischenzustand (% Zwischenzustand eines Supraleiters) erhalten. Die
% Kohärenzlänge eines Supraleiters erster Art
muû gröûer als die Eindringtiefe eines magnetischen Feldes sein, was nur bei einer groûen
% mittleren freien Weglänge der Leitungselektronen im normalleitenden Zustand der Fall
ist. Deshalb sind im allgemeinen nur reine metallische Elemente Supraleiter erster Art.
Supraleiter zweiter Art, % Supraleiter mit negativer Oberflächenenergie zwischen supraund normalleitender Phase (% Supraleitung).
Supraleiter zweiter Art zeigen nur unterhalb des
unteren kritischen Feldes den % Meiûner-Ochsenfeld-Effekt. Zwischen unterem kritischem
Feld und oberem kritischen Feld befinden sie
sich im % gemischten Zustand eines Supraleiters; zwischen oberem kritischem Feld und dem
kritischen Feld der Oberflächensupraleitfähigkeit sind sie im Zustand der Oberflächensupraleitfähigkeit. Die % Kohärenzlänge eines
Supraleiters zweiter Art ist kleiner als die Eindringtiefe eines magnetischen Feldes, was nur
bei einer kleinen % mittleren freien Weglänge
der Leitungselektronen im normalleitenden
Zustand der Fall ist. Deshalb sind im allgemeinen % Legierungen Supraleiter zweiter Art.
Supraleitfähigkeit % Supraleitung.
Supraleitung, Phänomen, bei dem einige Metalle (% Supraleiter) bei einer sog. % Sprungtemperatur Tc sprunghaft ihren % elektrischen
Widerstand verlieren und der % Meiûner-Ochsenfeld-Effekt auftritt. Abhängig davon, wann
die betrachtete Probe supraleitend wird, werden
% Supraleiter erster Art und % Supraleiter zweiter Art unterschieden. Die Supraleitung kann als
eine Manifestation der % Suprafluidität gesehen
werden, wobei die % Leitungselektronen des
Metalls die »Flüssigkeit« bilden (% Bändermodell).
Supraleitung und Suprafluidität
Dietrich Einzel, Garching
Dieses Essay befaût sich mit einer einheitlichen
theoretischen Betrachtung der Supraleitung in
Metallen und der Suprafluidität in elektrisch
neutralen Fermisystemen. Es soll aufgezeigt
werden, warum dieses faszinierende Phänomen
auch heute noch ± fast ein Jahrhundert nach
seiner experimentellen Entdeckung und fast ein
halbes Jahrhundert nach seiner ersten theoretischen Deutung ± Gegenstand intensiver
Forschung ist. Im ersten Abschnitt wird das
völlig unterschiedliche Verhalten des Normalzustands dieser Systeme mit dem des Suprazustands kontrastiert und es werden einige wichtige Aspekte der historischen Entwicklung dieses Forschungsgebietes nachgezeichnet. Dann
wird eine allgemeine Klassifizierung supraleitender und suprafluider Fermisysteme nach der
Symmetrie ihres Grundzustands durchgeführt.
Der nächste Abschnitt beschäftigt sich mit den
Gleichgewichtseigenschaften dieser Systeme bei
endlicher Temperatur. Schlieûlich wird die
Frage aufgeworfen, wie die Supraleitung und die
Suprafluidität auf äuûere Störungen reagiert
und was man daraus über die innere Struktur
und die Symmetrie der supraleitenden und superfluiden Phase lernen kann. Suprafluidität in
% Bosonen-Systemen wird an anderer Stelle behandelt (% Suprafluidität).
1 Normal- und Suprazustand
In normalen Metallen beruht der elektrische
Widerstand auf der Streuung der Leitungselektronen an thermischen Gitterschwingungen
(% Phononen) und an % Gitterfehlern (Verunreinigungen, Fehlstellen, Versetzungen, Korngrenzen, etc.), die durch eine Streurate 1=te
229
beschrieben wird. Die elektrische Stromdichte
je relaxiert gemäû
q
1
F
‡
j ˆ en :
qt te e
m
Hier bezeichnen n ˆ N=V die Teilchendichte, e und m die elektronische Ladung und
Masse. Die treibende Kraft F ˆ eE ist die elektrische Feldstärke E ˆ rf …1=c†qA=qt, die
sich wie üblich aus den elektromagnetischen
Potentialen f und A ableiten läût. Die elektrische Leitfähigkeit s e charakterisiert den Zusammenhang zwischen Stromdichte und elektrischem Feld:
ne2 te
je ˆ s e E ; s e ˆ
:
…1†
m
Dieser Zusammenhang ist als Drude-Gesetz
(% Drude-Lorenz-Theorie) bzw. als % Ohmsches
Gesetz bekannt. Ihr Kehrwert, der elektrische
Widerstand Re ˆ 1=s e , ist proportional zur
Impulsrelaxationsrate 1=te . Im Grenzfall T ! 0
verschwinden die Phononen, und der ausschlieûlich durch Defekte verursachte (Rest-)
Widerstand von sehr sauberen Metallen kann
sehr gering sein.
Im Jahre 1911 studierte Heike % Kamerlingh
Onnes in Leiden diese Effekte an Quecksilber im
Temperaturbereich zwischen 1 und 5 K. Er kam
zu dem überraschenden Resultat, daû der
elektrische Widerstand Re , anstatt stetig auf den
Restwiderstandswert abzusinken, bei einer kritischen Temperatur Tc ˆ 4,2 K verschwand.
Dieses Phänomen (Re ˆ 0, s e ˆ 1) wird seitdem Supraleitung genannt. Die wohl beeindruckendste Konsequenz des Supraleitungsphänomens demonstrierte Kamerlingh Onnes,
indem er einen Strom in einem supraleitenden
Bleiring bei 4 K in Gang setzte, die Stromquelle
abschaltete und einen Dauerstrom % (Dauerstrom, supraleitender) über ein ganzes Jahr
ohne meûbare Reduktion beobachten konnte.
Kamerlingh Onnes Entdeckung wurde im Jahre
1913 mit dem Physik-Nobelpreis gewürdigt.
Daû das Phänomen der Supraleitung noch
mehr beinhaltet als das bloûe Verschwinden des
elektrischen Widerstandes unterhalb einer
Sprungtemperatur Tc , zeigten Walther % Meiûner und Robert % Ochsenfeld im Jahre 1933. Sie
entdeckten, daû Supraleiter Magnetfelder reversibel aus ihrem Inneren verdrängen oder
abschirmen, und zwar unabhängig davon, ob
man den Supraleiter im Magnetfeld abkühlt
(Verdrängungseffekt) oder erst unterhalb der
Sprungtemperatur Tc ein Magnetfeld anlegt
(Abschirmeffekt). Der Supraleiter verhält sich
somit wie ein idealer Diamagnet. Diese Feldverdrängungseigenschaft der Supraleiter ist
nach ihren Entdeckern % Meiûner-Ochsenfeld±
Effekt benannt geworden.
Parallel zu dieser Entdeckung entwickelten
die Brüder Fritz und Heinz % London, aber auch
Max von % Laue, die phänomenologische sog.
London-Laue-Theorie der Supraleitung (1935±
1938), in der eine makroskopische Anzahl supraleitender Teilchen der Ladung q* und der
Masse m*, die sich in den elektromagnetischen
Supraleitung und Suprafluidität
Potentialen f und A bewegen, durch eine kollektive quantenmechanische Wellenfunktion
y ˆ a exp…if† mit Amplitude a und Phase f
beschrieben wird. Im Gegensatz zur Interpretation der gewöhnlichen % Quantenmechanik von a2 …r, t† als Wahrscheinlichkeitsamplitude, ein Teilchen am Ort r zur Zeit t
vorzufinden, wurde a2 ˆ ns mit der makroskopischen Teilchenzahldichte der supraleitenden Ladungsträger verknüpft. Ansonsten
konnten alle aus der Quantenmechanik bekannten Resultate übernommen werden, insbesondere die Tatsache, daû der SchrödingerGleichung für y die Kontinuitätsgleichung für
die Kondensat-Dichte q*qns =qt ‡ r js
q ˆ0
äquivalent ist, in der die Ladungssuprastroms
dichte jq die Form
ns q* n
q* o
hrf
A
…2†
jsq ˆ
m*
c
hat. Die einzelnen Ladungsträger verlieren somit ihre Individualität völlig, denn sie gehorchen kollektiv den Gesetzen der Quantenmechanik. Obwohl diese Theorie nichts über den
Mechanismus, der zur Supraleitung führt, aussagt, betrachtet sie die Supraleitung erstmals als
makroskopisches Quantenphänomen und kann
Dauerströme, Magnetfeldabschirmung, charakterisiert durch die sog. Londonsche Magnetfeldeindringtiefe (% Londonsche Theorie
der Supraleitung)
m*c2
l2L ˆ
,
4pns q2
sowie die sehr viel später entdeckte % Fluûquantisierung durch einen Supraleiter vorhersagen.
Wegen der Eindeutigkeitsforderung
†
dr rf ˆ 2pn, n ˆ 0, 1, . . ., an y ergibt
sich für das (Fluû-) Integral über die Querschittsfläche S eines supraleitenden Hohlzylinders
… die Bedingung
hc
F' ˆ dS H' ˆ nF0 ; F0 ˆ
; n ˆ 0, 1, . . . ,
q*
S
in der H' ˆ H ‡ …4p=c†l2L r jsq und F0 das
Quantum des magnetischen Flusses darstellt.
Im Jahre 1961 gelang Robert Doll und Martin
Näbauer (unabhängig davon aber auch Deaver
und Fairbanks) schlieûlich der experimentelle
Beweis dafür, daû die Gröûe F' quantisiert ist.
Das experimentell bestimmte Fluûquantum lieû
den Schluû zu, daû beim Ladungstransport in
Supraleitern nicht, wie in der London-Theorie
angenommen, einzelne (q* ˆ e, m* ˆ m,
ns ˆ ns ), sondern Paare von Elektronen mit
der doppelten Elementarladung (q* ˆ 2e,
m* ˆ 2m, ns ˆ ns =2† beteiligt sind.
Wie die Metallelektronen zeigen auch elektrisch neutrale Flüssigkeiten in ihrem Normalzustand das Phänomen eines Strömungswiderstands. Die Massenstromdichte jm genügt der
Relaxationsgleichung
q
1
h 2
‡
r jm …r, t† ˆ nF…r, t† ,
qt tm r
in der die treibende Kraft F ˆ rP=n in der
Regel ein Druckgradient ist. Im Gegensatz zur
Supraleitung und Suprafluidität
230
Relaxationsrate des elektrischen Stroms gilt
1=tm ˆ 0, da weder Phononen noch Fehlstellen
existieren und Zweiteilchenstöûe wegen des
Fehlens von Umklappprozessen nicht zur Impulsrelaxation führen. Die Relaxation ist deshalb diffusiv und durch die Scherviskosität h
(% Viskosität) bestimmt. Diese vermittelt auch
den Zusammenhang zwischen dem querschnittsgemittelten Massenstrom hjm i der
Flüssigkeit und dem von auûen angelegten
Druckgefälle, der als % Hagen-Poiseuillesches
Gesetz bekannt ist. Für Strömung zwischen
parallelen Platten (Abstand d) gilt
hjm i ˆ s m
F
nm2 d2
; sm ˆ
:
m
12h
…3†
Der Strömungswiderstand Rm ˆ 1=sm ist
somit proportional zur Scherviskosität der
Flüssigkeit. Seine Beobachtbarkeit zu tieferen
Temperaturen hin wird verdeckt durch die in
fast allen Fällen eintretende Verfestigung dieser
Systeme. Nur Flüssigkeiten, die aus besonders
leichten Atomen (wie zum Beispiel die Isotope
des Heliums 4He und 3He) bestehen, bleiben bis
zum absoluten Temperaturnullpunkt bei Atmosphärendruck flüssig. Man nennt diese Systeme % Quantenflüssigkeiten, da ihr flüssiger
Zustand durch die quantenmechanischen
% Nullpunktsbewegungen hervorgerufen wird.
Im Jahre 1971 entdeckten David % Lee, Douglas % Osheroff und Robert % Richardson bei
einer Sprungtemperatur Tc von etwa zwei Tausendstel K den Übergang von flüssigem 3He in
zwei superfluide Phasen. Obwohl im Gegensatz
zur Impulsrelaxation die Scherviskosität
scheinbar verschwindet, wies ihr Verhalten sehr
viele Analogien zur Supraleitfähigkeit der
»Elektronenflüssigkeit« in Metallen auf, zeigte
zusätzlich aber eine Vielzahl neuer und exotischer Eigenschaften. Diese Entdeckung löste
eine wahre Flut von experimentellen und theoretischen Veröffentlichungen aus, die über mehr
als zwei Dekaden anhielt und schlieûlich im Jahr
1996 mit dem Physik-Nobelpreis für die drei
Entdecker ihre Würdigung fand.
Auch für neutrale suprafluide Fermi-Systeme
mit Teilchen der Masse m* ˆ 2m und der superfluiden Dichte ns ˆ ns =2 läût sich die
London-Theorie anwenden. Wegen der fehlenden Ladung ist der supraleitende Massenstrom jetzt allein mit der räumlichen ¾nderung
der Phase der Kondensat-Wellenfunktion verknüpft:
h
…4†
jsm ˆ ns rf :
2
Die wesentliche Gemeinsamkeit der Phänomene Supraleitung und Suprafluidität läût sich
nur mit den Denkmethoden der Quantenmechanik verstehen. Sie besteht darin, daû es sich
bei Elektronen und 3He-Atomen, welche Vielteilchensysteme von typischerweise 1023 Teilchen bilden, um % Fermionen handelt, d.h.
Teilchen mit einem halbzahligen % Spin.
Fermionen gehorchen dem % Pauli-Prinzip,
welches besagt, daû nur ein Fermion einen gegebenen Quantenzustand fk, sg, charakterisiert
durch den Impuls hk und die Spinprojektion s,
besetzen kann. (Bei flüssigem 4He handelt es
sich um ein Bosonen-System.)
Ein moderner Zugang zu den Phänomenen
Supraleitung (geladene Fermionen, Elektronen)
und Suprafluidität (neutrale Fermionen) sollte
diese auf ein und derselben Stufe behandeln. Ein
erster Schritt in diese Richtung lieû sehr lange,
nämlich bis zum Jahre 1957, auf sich warten. In
diesem Jahr veröffentlichten die Theoretiker
John % Bardeen, Leon % Cooper und Robert
% Schrieffer (BCS) ihre mikroskopische Theorie
der Supraleitung, nicht ahnend, daû sich diese
Theorie, nach einigen nicht unwesentlichen
Modifikationen, die insbesondere dem Theoretiker Anthony J. Leggett zu verdanken sind,
auch zur Beschreibung der Suprafluidität von
flüssigem 3He eignen würde. Wegen ihrer universellen Anwendbarkeit wurde die % BCSTheorie im Jahre 1972 mit dem Physik-Nobelpreis gewürdigt.
2 Klassifizierung paarkorrelierter FermiSysteme
Fermi-Systeme lassen sich durch ihre Teilchendichte n ˆ …2mEF †3=2 =…3p2 h
3 †, mit EF der
% Fermi-Energie, das Energiespektrum ek ˆ
xk ‡ m, mit m dem chemischen Potential
(EF ˆ m…T ˆ 0†), die Gruppengeschwindigkeit
vk ˆ rk xk =h und die Zustandsdichte an der
Fermi-Kante NF ˆ dn=dEF ˆ 3n=2EF charakterisieren. Im globalen thermodynamischen
Gleichgewicht wird die mittlere Besetzungswahrscheinlichkeit dieser Zustände durch die
Impulsverteilung
y
…5†
nk ˆ n…xk † ˆ h^cks ^cks i
y
beschrieben. Hier bedeuten c^ks und c^ks die
Erzeugungs- und Vernichtungsoperatoren für
ein Fermion im Quantenzustand fk, sg und hi
der statistische Mittelwert. Im Normalzustand
des Fermi-Systems ist nk ˆ 1=‰exp…xk =kB T†
‡ 1Š die Fermi-Dirac-Verteilung (% Fermi-Dirac-Statistik).
Das BCS-Modell postuliert, daû es bei tiefen
Temperaturen energetisch günstiger ist, wenn
sich ein temperaturabhängiger Teil der Fermionen
zu sog. % Cooper-Paaren formiert. Der geniale
Aspekt an der Paarungshypothese ist die Einsicht, daû die Paarung nicht im Orts- sondern
im Impulsraum stattfindet. So ist die zentrale
Annahme der BCS-Theorie die spontane Paarformation im k-Raum, beschrieben durch einen
im thermodynamischen Gleichgewicht endlichen
statistischen Mittelwert, die Paaramplitude
gks1 s2 h^c
cks2 i
ks 1 ^
6ˆ 0 ; T Tc :
…6†
Hier ist h
k ˆ h
…k1 k2 † der Relativimpuls
des Paares. Das Pauli-Prinzip erzwingt die totale
Antisymmetrie von gks1 s2 beim Vertauschen
der Spins s 1 , s 2 und der Impulse k1 , k2 :
g
ks2 s 1
ˆ
gks1 s2 :
…7†
Die Spinabhängigkeit der Paaramplitude
wird durch die Möglichkeiten, zwei Spins vom
231
Supraleitung und Suprafluidität
Betrag h=2 und mit den Projektionen s 1 , s 2 zum
Gesamtspin s und der Gesamtprojektion ms zu
koppeln, festgelegt. Der % Clebsch-Gordon-Koeffizient für diese Kopplung lautet
!
1
1 s
2
2 ˆ
s 1 s 2 ms
0
1
p1 dm , 0
ds, 1 dms , 1
s
2
@
A
s‡1
… p
1†
dms , 0 ds, 1 dms , 1
2
s1 s 2
und läût nur die beiden Fälle s ˆ 0 (SingulettPaarung) und s ˆ 1 (Triplett-Paarung) zu. Für
Singulett-Paarung gilt
0
gk
ˆ gk …it2 †s1 s2 ,
gks1 s2 ˆ
gk 0 s 1 s 2
wobei gk ˆ 12 ‰gk#" gk"# Š. Hier ist t2 eine der
% Pauli-Matrizen, die zusammen mit der Einheitsmatrix t0 ein vollständiges Basissystem
von 2 2-Matrizen bilden.
Wegen Gl. (7) muû gk für Singulett-Paarung
gerade Parität bezüglich k haben, g k ˆ gk . Die
k-Abhängigkeit von gk läût sich mit einer orbitalen Quantenzahl l klassifizieren, und man
spricht von s-Wellen-Paarung (l ˆ 0), d-Wellen-Paarung (l ˆ 2) u.s.w. Im Fall der SpinTriplett-Paarung hat man
!
1 ‰g ‡ g Š
gk""
k"#
2 k#"
gks1 s2 ˆ 1
gk##
2 ‰gk#" ‡ gk"# Š
s s
1
ˆ g k …tit2 †s1 s2 :
Die Triplett-Komponenten g kx ˆ 12 gk##
2
gk"" ,
g ky ˆ 2i1 …gk"" ‡ gk## †, und g kz ˆ 12 …gk#" ‡ gk"# †
p
p
Die skalaren und vektoriellen Paaramplituden gk , g k , oder äquivalent dazu, die
Paarpotentiale Dk und d k , werden auch als
Ordnungsparameter (% Phasenübergänge) der
supraleitenden oder superfluiden Phase des
paarkorrelierten Fermi-Systems bezeichnet. Die
Dk ˆ D0 …T†f …k† ; d k ˆ D0 …T†f …k†
in den temperaturabhängigen Maximalwert
D0 …T† und einen k-abhängigen orbitalen Anteil,
der die Möglichkeit einer Anisotropie auf der
% Fermi-Fläche enthält. Man kann in unterschiedlichen Fermi-Systemen die Symmetrie
des Paarpotentials mit der der Fermi-Fläche
bzw. der Bandstruktur vergleichen. Sind diese
Symmetrien gleich (oder ist nur die Eichsymmetrie spontan gebrochen), so wird die Paarung
als konventionell (k) bezeichnet. Ist die Symmetrie des Paarpotentials geringer als die der
Fermi-Fläche (oder gibt es neben der Eichsymmetrie noch zusätzliche spontan gebrochene
Symmetrien), so nennt man die Paarung unkonventionell (u).
In die siebziger und achtziger Jahre fiel die
Entdeckung neuer, exotischer Supraleiter. Dazu
gehören % organische Supraleiter und Supraleiter mit sog. % schweren Fermionen. Im Jahre
1986 wurden Materialien auf Kupferoxidbasis
(Kuprate) mit Sprungtemperaturen bis zu 153 K
(sog. % Hochtemperatur-Supraleiter) durch Karl
Alex % Müller und Georg % Bednorz entdeckt,
die dafür im Jahr darauf mit dem Nobelpreis für
Physik geehrt wurden. Man ist heute davon
überzeugt, daû die superfluiden Phasen des 3He,
u.a. der % Schwerfermionensupraleiter UPt3,
sowie alle lochdotierten (ld) Kuprat-Supraleiter
einen unkonventionellen Ordnungsparameter
haben. Unerwarteterweise zeigen die elektrondotierten (ed) Kuprate scheinbar konventionelles Verhalten. Eine spezielle Konsequenz
dieser Unkonventionalität ist die Tatsache, daû
der Ordnungsparameter Nulldurchgänge oder
Noden haben kann, d.h. er kann auf der FermiFläche Punkt- (P) oder Linien- (L) förmige
Nullstellen haben. Dieser Sachverhalt ist in
Abb. 1 veranschaulicht. In Tab. 1 sind die Eigenschaften einiger wichtiger supraleitender (SL)
und superfluider Fermi-Systeme zusammengestellt. Die Fermi-Flächen werden der Einfachheit halber als sphärisch (D ˆ 3) oder als zylindrisch (D ˆ 2) angenommen. Aufgeführt sind
Ordnungsparametersymmetrie, Nodenstruktur
und die Dimensionalität D ihrer Fermi-Fläche.
∆
0
Fe r
mi
fl ä
|∆
k
ch
|
e
T
kB
des Paaramplituden-Vektors g k sind den magnetischen Quantenzahlen ms ˆ 1, 0, 1 zugeordnet und haben wegen (7) ungerade Parität
bezüglich k, g k ˆ g k . Im Fall der TriplettPaarung ist die orbitale Quantenzahl l ungerade
und man spricht von p-Wellen-Paarung (l ˆ 1),
f-Wellen-Paarung (l ˆ 3) u.s.w. Man erkennt,
daû mit dem supraleitenden Phasenübergang
eine spontan gebrochene Symmetrie verknüpft
ist, nämlich die bezüglich der lokalen Eichtransformation ^cks ! ^cks exp…if=2†, bei der
die Paaramplitude gks1 s2 in gks1 s2 exp…if†
übergeht (% spontane Symmetriebrechung). Die
Formation von Cooper-Paaren wird durch eine
in der Nähe der Fermi-Kante anziehende
…s†
Wechselwirkung G kp vermittelt, welche die
mittleren Paaramplituden gk und g k mit einer
neuen Energieskala, dem mittleren sog. Paarpotential X
verknüpft:
X …1†
…0†
Dk ˆ
G kp gp ; dk ˆ
G kp g p : …8†
Cooper-Paare, deren Gesamtheit man auch als
Kondensat bezeichnet, bilden nun den neuartigen kollektiven Zustand makroskopischer
Quantenkohärenz, der bereits in der LondonTheorie antizipiert worden ist. Durch die Paarungshypothese liefert die BCS-Leggett-Theorie
im Gegensatz zur London-Theorie nicht nur
den korrekten Wert für das im Doll-NäbauerExperiment bestimmte Fluûquantum, sondern
erlaubt auch eine korrekte Beschreibung der
thermodynamischen, elektromagnetischen, hydrodynamischen und spindynamischen Eigenschaften supraleitender und superfluider Fermi-Systeme.
Im folgenden sollen nun einige der in der
Natur vorkommenden paarkorrelierten FermiSysteme durch die Form ihrer Paarpotentiale
charakterisiert werden. Hierzu zerlegen wir
Supraleitung und Suprafluidität 1: Skizze einer Node
im Paarpotential. Die offenen
Kreise symbolisieren thermische Anregungen (BogoljubowQuasiteilchen) für den Fall
kB T < D0 …T†.
Supraleitung und Suprafluidität
232
Supraleitung und Suprafluidität 1: Ordnungsparameter einiger Fermi-Systeme.
System
Paarung
Anisotropie
Bezeichnung D Noden
Klass. SL
s ˆ 0, l ˆ 0
k f …k† ˆ 1
isotrop
3
±
3
He-A
s ˆ 1, l ˆ 1
u f …k† ˆ sin qd^
axial
3
P
3
He-B
s ˆ 1, l ˆ 1
u f …k† ˆ R…^
n, V† ^k
pseudoisotrop 3
±
s ˆ 0, l ˆ 2
u f …k† ˆ 2p
sin
E1g
3 P‡L
UPt3
 q cos q
3 3 2
s ˆ 1, l ˆ 3
u f …k† ˆ
sin q cos qd^ E2u
3 P‡L
2
2
2
2
L
Kuprat-SL (ld) s ˆ 0, l ˆ 2
u f …k† ˆ cos 2f
B1g , dx y
Kuprat-SL (ed) s ˆ 0, l ˆ 0, 2…?† (?) f …k† 1
(?)
2
±
In Tab. 1 ist 0 q p der (Polar-) Winkel
zwischen einer für den Paarzustand charakteristischen makroskopischen orbitalen Vorzugsrichtung `^ und dem Einheitsvektor ^k auf
der Fermi-Fläche. Für den Fall der TriplettPaarung ist dà eine makroskopische Vorzugsrichtung im Spinraum. R…n, V† ist eine Rotationsmatrix, welche im Spezialfall des pseudoisotropen Zustands die Korrelation zwischen
Spin- und Bahnfreiheitsgraden der CooperPaare beschreibt. Der Winkel V spielt dabei die
gleiche Rolle wie der Winkel zwischen dà und `^
und reflektiert eine von Leggett erstmals diskutierte zusätzliche spontan gebrochene Symmetrie, nämlich die relative Spin-Bahn-Symmetrie des superfluiden Fermi-Systems (und
damit den unkonventionellen Charakter des
Ordnungsparameters). Da es sich bei den Kupraten um Quasi-2-D-Systeme handelt, wird die
dx2 y2 -Symmetrie des Paarpotentials durch den
(Azimuth-) Winkel 0 f 2p beschrieben.
3 Paarkorrelierte Fermi-Systeme im
thermischen Gleichgewicht
In der BCS-Behandlung werden die Paarwechselwirkungseffekte durch einen HamiltonOperator in % Molekularfeldnäherung erfaût.
Die folgende Diskussion wird nun der Übersichtlichkeit wegen auf den Fall der SingulettPaarung beschränkt. Die Resultate lassen sich
jedoch problemlos auf den Triplett-Fall verallgemeinern. Kombiniert man fermionische Erzeugungs- und Vernichtungsoperatoren zu einer zweikomponentigen Gröûe, einem sog.
^y ˆ f^cy , ^c k# g, dann ist dieser Ha% Spinor C
k
k"
milton-Operator formal dem des Normalzu%
stands äquivalent
X( Nambu-Formalismus),
y
H^MF ˆ
…9†
C^k xk C^k ‡ const:
k
Hier ist xk jedoch eine Energiematrix
xk Dk
xk ˆ
,
D*k
xk
in deren Diagonale die typischen Energien für
teilchenartige (xk > 0) und lochartige (xk < 0)
Anregungen stehen. Das mittlere Paarpotential
bildet die Nebendiagonalelemente und führt zu
einer Mischung von Teilchen- und Lochbeiträgen zur Energie. Wegen der spontanen
Paarformation Dk 6ˆ 0 für T Tc spricht man
im Zusammenhang mit dem Phänomen der
Supraleitung und der Suprafluidität auch von
nebendiagonaler langreichweitiger Ordnung.
Der Hamilton-Operator bzw. die Energiematrix werden diagonalisiert durch die % Bogoljubow-Walatin-Transformation
y
y
y
C^k ˆ a^k Bk ,
!
uk v k :
y
y
a^k ˆ fa^k" , a^ k# g , Bk ˆ
v*k uk
Da die neuen Erzeugungs- und Vernichtungsoperatoren wieder fermionische Anregungen beschreiben, gilt u2k ‡ v 2k ˆ 1. Man
erhält
Ek Dk
y
Bk xk Bk ˆ
y
Dk
Ek
Die Bedingung Dk 0 legt die Amplituden
uk und v k fest: u2k ˆ 12 …1 ‡ xk =Ek †, v 2k ˆ
1 u2k , wobei
q
Ek ˆ
xk ‡ D2k :
…10†
Die physikalische Bedeutung von Ek erkennt
man aus der Form des transformierten Hamilton-Operators
X
^ yks a
^ ks :
Ek a
…11†
H^MF ˆ UBCS …0† ‡
ks
Der erste Term in (11) ist die Gesamtenergie
des BCS-Grundzustands, während der zweite
Term den Beitrag der thermischen Anregungen,
der sog. Bogoljubow-Quasiteilchen bei endlichen Temperaturen beschreibt. Ek ist somit
das Energiespektrum der Bogoljubow-Quasiteilchen. Das Paarpotential Dk spielt damit die
Rolle einer im allgemeinen anisotropen
% Energielücke im Spektrum der thermischen
Anregungen. Die thermischen Eigenschaften
der Bogoljubow-Quasiteilchen werden durch
die Verteilungsfunktion
y
nk ˆ n…Ek † ˆ h^
aks a^ks i
1
ˆ
…12†
exp…Ek =kB T† ‡ 1
und ihre Ableitung nach Ek , fk ˆ qn…Ek †=
qEk ˆ 1=4kB T cosh2 …Ek =2kB T† beschrieben.
Im globalen thermodynamischen Gleichgewicht
ergibt sich die diagonale Verteilungsfunktion nk
(vgl. (5)) nach der Bogoljubow-Walatin-Transformation zu
nk ˆ u2k nk ‡ v 2k …1 nk † :
…13†
Es ist bemerkenswert, daû die Ableitung von
nk , Fk qnk =qxk ˆ …x2k =E2k †fk ‡ …D2k =2E3k †
…1 2nk †, bei „allen Temperaturen T Tc der
Summenregel 11 dxk Fk ˆ 1 genügt.
Die Gleichgewichts-Paaramplitude (vgl. (7))
lautet nach der Bogoljubow-Walatin-Transformation
Dk
E
gk ˆ uk v k …1 2nk † ˆ
tanh k : …14†
2Ek
2kB T
Die Ursachen und Mechanismen für die
…s†
Paaranziehung G kp < 0 sind unterschiedlich.
Bei konventionellen Supraleitern vermitteln
meistens die Quanten der Gitterschwingungen,
die Phononen, eine Paaranziehung zwischen
den Elektronen. In einigen Klassen unkonventioneller Supraleiter (Schwerfermion-, Hochtemperatur-Supraleiter sowie die superfluide
% Fermi-Flüssigkeit 3He) glaubt man heute, daû
233
Supraleitung und Suprafluidität
antiferromagnetische bzw. ferromagnetische
sog. Spinfluktuationen oder Paramagnonen die
Paaranziehung verursachen. Wir müssen an
dieser Stelle auf eine Diskussion der mikroskopischen Ursachen für die Paarattraktion
verzichten und nehmen lediglich an, daû
…s†
die Paarwechselwirkung sehr klein (jNF G kp j
1) ± wegen dieser Annahme spricht man im
Zusammenhang mit Supraleitung und Suprafluidität auch vom Limes schwacher Kopplung ±
und in einer Energieschale der Dicke ec EF
um die Fermi-Energie anziehend ist. Die Lösung
der Energielückengleichung (8) bei endlichen
Temperaturen geschieht durch Einsetzen der
Paaramplitude (14) in Gl. (8) und liefert bei der
Sprungtemperatur und bei T ˆ 0 die beiden im
Limes schwacher Kopplung universellen sog.
BCS-Mühlschlegel-Parameter, nämlich den für
die Molekularfeldnäherung typischen Sprung in
der spezifischen Wärme bei Tc und die Energielücke bei T ˆ 0:
2 2
DC C…Tc † CN …Tc‡ † 3 8 hfp iFS
ˆ
ˆ
CN
2 7z…3† hfp4 iFS
CN …Tc‡ †
0
1
D
hD2p ln Dp0 iFS
D0 …0†
A
ˆ p= exp@g ‡
kB Tc
hD2p iFS
Hier ist g ˆ 0, 577 . . . die Eulersche Konstante, z…3† ˆ 1, 202 . „. . die Riemannsche zFunktion; h. . .iFS ˆ …dW=4p† . . . bedeutet
eine Mittelung über die Fermi-Fläche und
CN …T† ˆ NF …p2 k2B T†=3 ist die Wärmekapazität
des normalen Fermi-Systems. In Tabelle 2 findet
man eine Zusammenstellung von BCS-Mühlschlegel-Parametern für einige repräsentative
paarkorrelierte Fermi-Systeme. Für Temperaturen 0 T Tc läût sich die maximale Energielücke wie folgt interpolieren:
D0 …T† ˆ
r
Tc
2 DC 1
B Tc
D0 …0† tanh pk
1
: …15†
3 CN hf 2 i
T
D …0†
0
p FS
4 Paarkorrelierte Fermi-Systeme in
äuûeren Feldern
Schlieûlich untersuchen wir, wie supraleitende
und superfluide Fermi-Systeme auf die Gegenwart räumlich und zeitlich schwach veränderlicher äuûerer Störungen wie ein Vektorpotential A, ein Magnetfeld H oder eine lokale Temperaturänderung dT bei beliebigen Temperaturen 0 T Tc reagieren. Eine solche Situation läût sich besonders einfach durch die AnSupraleitung und Suprafluidität 2: BCS-Mühlschlegel-Parameter einiger Fermisysteme.
isotrop
12
7z…3†
1,426
D0 …0† p
g
kB Tc e
1,764
DC
CN
axial E1g
10
6
7z…3† 5z…3†
1,188 0,998
pe5=6
pe47=30
2eg
4eg
2,029 2,112
E2u
286
245z…3†
0,971
p 177=70
3pe
18eg
2,128
dx2 y2
8
7z…3†
0,951
2p
1
eg‡2
2,140
nahme des sog. lokalen Gleichgewichts beschreiben. Das bedeutet, daû die Impulsverteilung n…Ek † der Bogoljubow-Quasiteilchen
auch in Gegenwart der Störungen noch eine
Fermi-Funktion nloc …Eks † ist,
!
h
qEk
Ek ec vk A g
2 sH ‡ qT dT
,
nloc …Eks † ˆ n
kB …T ‡ dT†
in der aber das Argument von Ek nach Eks ˆ
h=2†sH Qk dT verschoEk …e=c†vk A …g
ben ist, wobei Qk ˆ Ek =T qEk =qT und g das
% gyromagnetische Verhältnis der Fermionen
ist. Die lokale % lineare Antwort (linear response) des gesamten Quasiteilchensystems
führt bei einer Temperaturänderung dT auf die
Entropieänderung TdsB ˆ CB dT, beim Anlegen eines Magnetfeldes H auf die Spinmagnetisierung MB ˆ cB H und bei Anwesenheit
des Vektorpotentials A auf den elektronischen
Quasiteilchenstrom jB ˆ …e2 =c†K B A. Die entsprechenden sog. Responsefunktionen sind die
% Wärmekapazität CB …T†, die % Paulische
Spinsuszeptibilität cB …T† und der Stromresponse-Tensor K B …T†. Im folgenden fassen wir
die Resultate für diese Gröûen bei beliebigen
Temperaturen zusammen (bei den numerischen
Rechnungen wurde die Interpolationsformel
(15) für D0 …T† verwendet):
1. Wärmekapazität der Bogoljubow-Quasiteilchen:
1 X dnloc …Eks †
CB …T† ˆ
E
V ks k
dT
!
E2k 1 qD2k
1X
: …16†
f
ˆ
V ks k T 2 qT
Abb. 2 zeigt die Temperaturabhängigkeit der
normierten Wärmekapazität CB …T†=CN …T† für
einige paarkorrelierte Fermi-Systeme. Die Resultate für den E1g - und E2u -Zustand liegen sehr
nahe an der Kurve für dx2 y2 -Paarung und sind
daher nicht eingezeichnet. Man beachte, daû
mit zunehmender Energielückenanisotropie die
Diskontinuität in CB …T† bei Tc in demselben
Maûe abnimmt wie der Anstieg von
CB …T†=CN …T† bei tiefen Temperaturen zunimmt (Entropie-Summenregel).
2. Spinsuszeptibilität der Bogoljubow-Quasiteilchen:
1 X gh dnloc …Eks †
s
cB …T† ˆ
V ks 2
dH
2 X
gh 1
f ˆ cN Y…T† : …17†
ˆ
2 V ks k
Hier ist cN ˆ …gh=2†2 NF die Paulische Spinsuszeptibilität des Normalzustands. Die Temperaturabhängigkeit der Spinsuszeptibilität
wird durch die dimensionslose
P sog. YosidaFunktion Y…T† ˆ …1=NF V† ks fk beschrieben. Abb. 3 zeigt die Temperaturabhängigkeit
der normierten Spinsuszeptibilität c…T†=cN für
einige paarkorrelierte Fermi-Systeme. Die Resultate für den E1g - und E2u -Zustand liegen sehr
nahe an der Kurve für dx2 y2 -Paarung und sind
2,5
C B (T )
C N (T )
2
dx 2 – y 2
1,5
1 dx 2 – y 2
Axial
0,5
Isotrop
0
0
1
0,2 0,4 0,6 0,8
T
Tc
Supraleitung und Suprafluidität 2: Temperaturabhängigkeit der normierten
Quasiteilchen-Wärmekapazität
CB …T†=CN …T† für einige paarkorrelierte Fermi-Systeme.
1
χ (T )
χN
0,8
Axial
0,6 Pseudoisotrop
dx 2 – y 2
0,4
0,2
Isotrop
0
0
0,2
0,4
0,6
0,8
1
T
Tc
Supraleitung und Suprafluidität 3: Temperaturabhängigkeit der normierten Spinsuszeptibilität c…T†=cN für einige
paarkorrelierte Fermi-Systeme.
Supraleitung und Suprafluidität
1
δ λ L (T )
λ L (0)
0,8
dx 2 – y 2
0,6
E1g ( )
0,4
E1g (II)
E2u
0,2
Isotrop
0
0
0,2
0,4
0,6
0,8
T
Tc
Supraleitung und Suprafluidität 4: Temperaturabhängigkeit der normierten
London-BCS-Magnetfeldeindringtiefe dlL …T†=lL …0† für einige typische Supraleiter.
1
daher nicht eingezeichnet. Besonders deutlich
wird der Unterschied zwischen dem thermisch
aktivierten konventionellen Verhalten und dem
linearen Tieftemperaturpotenzgesetz für die
Energielücken mit Liniennoden. Bei der Berechnung der Spinsuszeptibilität in Systemen
mit Spin-Triplett-Paarung ist zu beachten, daû
sich die ms ˆ 1-Komponenten des Tripletts
paramagnetisch verhalten, d.h. sie tragen einen
konstanten (Pauli-) Beitrag zur Suszeptibilität
bei. Die ms ˆ 0-Komponente repräsentiert den
Beitrag der thermischen Anregungen und verschwindet im Limes T ! 0. So stellt die temperaturabhängige Gröûe cB …T† im Fall von 3HeB nur den ms ˆ 0-Beitrag (13) des Spin-Tripletts
dar. Mit den fehlenden ms ˆ 1-Beiträgen (23)
lautet die gesamte Spinsuszeptibilität von
3
He-B c…T†=cN ˆ 23 ‡ 13 Y…T†, wenn Wechselwirkungseffekte vernachlässigt werden. Der
axiale Zustand zur Beschreibung von 3He-A
besitzt im einfachsten Fall (d^ ? ^z) nur die paramagnetischen ms ˆ 1-Komponenten des
Spin-Tripletts (man spricht deshalb auch von
»equal spin pairing«). Daher behält die Spinsuszeptibilität bei allen Temperaturen T Tc
ihren Normalzustands-(Pauli-)Wert. Für den
E2u -Zustand gilt im einfachsten Fall d^ ˆ ^z . Somit trägt nur die ms ˆ 0-Komponente des Tripletts zur Spinsuszeptibilität bei, c…T† ˆ cB …T†.
3. Stromresponse der Bogoljubow-Quasiteilchen
c1X
dnloc …Eks †
KBij …T† ˆ
v
e V ks ki
dAj
1X
ˆ
f v v :
…18†
V ks k ki kj
Die Gröûe K B beschreibt den Quasiteilchenbeitrag zum gesamten elektronischen SuprarL†, in dem K s ˆ
strom jse ˆ …e2 =c†K s …A ‡ P
K D K B und KDij ˆ …1=V† ks Fk v ki v kj der
diamagnetische Anteil des Stroms ist. Man beachte, daû das Vektorpotential durch einen
Phasengradienten ergänzt worden ist (Eichtransformation des Vektorpotentials A ! A ‡
rL), um dem Resultat für den Suprastrom eine
eichinvariante Form zu geben. Die Ersetzung
L ˆ …hc=2e†f verknüpft L mit der Variablen
f, welche die gebrochene Eichsymmetrie beschreibt. Somit sind die eichinvarianten Ausdrücke für den elektronischen Suprastrom
h
e
jse ˆ eK s rf
A
…19†
2
c
234
und den superfluiden Massenstrom aus der
BCS-Theorie
h
jsm ˆ mK s rf
…20†
2
formal identisch mit den entsprechenden Resultaten (2) und (4) der London-Theorie, mit
dem einzigen Unterschied, daû man die Gröûe
K s im Rahmen der BCS-Theorie berechnen
kann.
Für den Fall einer (uniaxialen) Anisotropie
^ ^c, mit a, b,
^) der Fermi-Fläche (^
^, b,
(Achse n
nˆa
c den Kristallachsen) oder der Energielücke
s ‰d
^ gilt K s ˆ K s n
^n
^ ‡ K?
^j Š. Der
^i n
(^
n ˆ `)
n
ij
k i j
ij
London-BCS-Strom, in die % Maxwell-Gleichung r B ˆ …4p=c†jse eingesetzt, beschreibt
die Magnetfeldabschirmung des Supraleiters,
charakterisiert durch die beiden London-BCSEindringtiefen l2Lk, ? ˆ c2 =4pe2 Kk,s ? . Für isos ˆ ns =m mit
trope Fermi-Systeme ist Kks ˆ K?
der superfluiden Dichte ns ˆ n‰1 Y…T†Š. In
Abb. 4 ist die Temperaturabhängigkeit der
normierten Magnetfeldeindringtiefe dlL …T† ˆ
lL …T† lL …0† für einige Supraleiter gezeigt.
Der Unterschied zwischen dem thermisch aktivierten Tieftemperaturverhalten für isotrope
Paarung und den linearen Tieftemperaturpotenzgesetzen für den Fall der Dominanz von
Liniennoden ist auch in dieser Gröûe deutlich.
Man beachte, daû die E1g - im Gegensatz zur
E2u -Energielücke eine starke Anisotropie in den
k , ?-Komponenten aufweist. Dies könnte für
die Identifikation der Ordnungsparametersymmetrie in UPt3 nützlich sein.
Das Tieftemperaturverhalten der lokalen
Responsefunktionen für isotrope Energielükken ist thermisch aktiviert,
limT!0 Y…T† ˆ
1
Y0 …T† ˆ …2pD0 =kB T†2 exp… D0 =kB T † und damit qualitativ unterschiedlich von dem für
Energielücken mit Nodenstruktur. Im letzteren
Fall existieren thermische Anregungen, in
Abb. 1 durch kleine Kreise symbolisiert, bei
tiefen Temperaturen kB T D0 besonders in der
Umgebung der Noden, was zu den in Abbildungen 2±4 sichtbaren Potenzgesetzen für
die Responsefunktionen führt. In Tabelle 3 sind
analytische Resultate für das Tieftemperaturverhalten der drei oben abgeleiteten Responsefunktionen für einige supraleitende und superfluide Systeme zusammengestellt.
Experimentelle Resultate sind im Fall der
superfluiden Phasen des 3He, lochdotierter
Kuprate und des Schwerfermionsupraleiters
Supraleitung und Suprafluidität 3: Tieftemperaturverhalten einiger paarkorrelierter Fermi-Systeme.
E2u
dx2 y2
Gröûe
isotrop
axial
E1g
2
1
1
2
2
CB …T†
D0
7p
kB T
27z…3† kB T
27z…3† kB T
27z…3† kB T 1
p


3Y
…T†
0
CN …T†
D0
4p
D0
p2
D0
pkB T
5
2p 3 D0
cB …T†
Y0 …T†
p2 kB T 2
p
kB T 1
p
kB T 1
kB T 1
p ln 2
2 ln 2
ln 2
cN
2
D0
D
D
3 D0
3
0
0
1
dlLk …T†
p2 k B T 2
p2 kB T 2
p ln…2† kB T 1
±
Y0 …T†
p


2
lL …0†
2
8
D0
D0
D0
2 3
1
dlL? …T†
7p4 kB T 4
3p ln…2† kB T 1
p ln…2† kB T 1
kB T 1
Y0 …T†
p


ln
2
2
lL …0†
30
D0
8
D0
D0
D0
2 3
235
Surfactant
Paarformation stellt hierbei den entscheidenden Aspekt der BCS-Theorie dar, unter dem sich
die Phänomene der Supraleitung und der Suprafluidität vereinheitlichen lassen, wenn auch
der Mechanismus, der zur Bildung der CooperPaare führt, in den verschiedenen Klassen supraleitender Systeme unterschiedlich sein kann.
UPt3 im Einklang mit der Annahme unkonventioneller Cooper-Paarung. Während die
Annahme von p-Wellen-Triplett-Paarung in
3
He-A und -B zu einem weitgehend quantitativen Verständnis von Thermodynamik, Transport, Spindynamik und der kollektiven Moden
geführt hat, lassen sich die lochdotierten Kuprate, zumindest bei optimaler Dotierung, qualitativ auf der Basis von Singulett-dx2 y2 -Paarung verstehen. Eine mögliche Dotierungsabhängigkeit der Paarsymmetrie ist Gegenstand
von gegenwärtigen Untersuchungen. Die Identifikation der Symmetrie des Ordnungsparameters in UPt3 ist noch nicht endgültig gesichert, jedoch sind die E1g - und E2u -Zustände
ernstzunehmende Kandidaten.
Zusammenfassend sei festgestellt, daû man
die Eigenschaften einer groûen Klasse paarkorrelierter Fermi-Systeme im Gleichgewicht
und in Gegenwart äuûerer Felder im Rahmen
einer erweiterten BCS-Theorie schwacher
Kopplung verstehen kann. Das Postulat der
M. Tinkham, Introduction to Superconductivity,
McGraw Hill, 1996;
J.R. Waldram, Superconductivity of Metals and
Cuprates, IOP Publishing Ltd, 1996;
J.B. Ketterson und S.N. Song, Superconductivity,
Cambridge University Press, 1999;
P.G. deGennes, Superconductivity in Metals and
Alloys, Perseus Books, 1999;
D. Vollhardt und P. Wölfle, The Superfluid
Phases of Helium 3, Taylor & Francis, 1990;
T. Tsuneto, Superconductivity and Superfluidity, Cambridge University Press, 1998.
Surface Acoustic Waves, SAW, akustische
Oberflächenwellen, OFW, Moden elastischer
Energie, die sich an der Oberfläche eines Festkörpers mit Schallgeschwindigkeit ausbreiten
können. Dabei fallen sämtliche mit der Welle
assoziierten Gröûen, wie z.B. die mechanische
Auslenkung der Oberfläche auf eine von der
genauen Struktur des Festkörpers abhängigen
Art und Weise etwa exponentiell über eine
Wellenlänge in die Tiefe des Körpers hinein ab.
SAW wurden 1885 erstmals theoretisch von
Lord % Rayleigh im Rahmen einer Arbeit über
Erdbeben beschrieben. Hier haben SAW und
deren Theorie bis heute eine groûe Bedeutung.
Technologisch werden SAW seit etwa 20 Jahren
im Bereich der Hochfrequenzsignalverarbeitung eingesetzt. Dabei werden sie auf piezoelektrischen Substraten (% piezoelektrischer Effekt), meist % Einkristallen, mit in Planartechnologie hergestellten Schallwandlern (engl.
transducer) angeregt. Auf piezoelektrischen
Substraten wird die mechanische Welle über die
Gitterdeformation von starken elektrischen
Feldern und Potentialen begleitet. Dadurch ist
eine effiziente Konversion eines hochfrequenten Signals (10 MHz±10 GHz) in eine SAW und
umgekehrt möglich. Auf Grund der im Vergleich zur % Lichtgeschwindigkeit geringen
% Schallgeschwindigkeit (ca. 3 km/s) bildet ein
solches Bauelement eine akustische % Verzögerungsleitung mit einem charakteristischen Frequenzgang. Solche Bauteile werden in groûer
Zahl als Hochfrequenzfilter (% Filter) im Mobilfunk, zur Frequenzselektion bei der Fernsehübertragung etc. eingesetzt. Besonderer
Vorteil der SAW-Filter ist ihre Robustheit, die
Reproduzierbarkeit und die Möglichkeit, den
gewünschten Frequenzgang des Filters über
relativ einfache Algorithmen aus der FourierTransformierten (% Fourier-Transformation)
des Schallwandler-Layouts zu berechnen. Auch
wesentlich komplexere Funktionen in der
Hochfrequenz-Signalverarbeitung lassen sich
mit Hilfe von SAW darstellen, die dann zum
Beispiel für die Verschlüsselung von Daten oder
für Identifikationszwecke (elektromagnetisches
Analogon zum Strichcode) eingesetzt werden.
Die Wechselwirkung akustischer Oberflächenwellen mit externen Randbedingungen, wie des
Umgebungsgasdrucks, eines Massenbelags der
Oberfläche, einer externen Verzerrung des
Substrates, elektrischen Ladungen oder starken
Magnetfeldern, kann zur Sensorik (% Sensoren)
herangezogen werden. Dabei wird im allgemeinen die durch die Wechselwirkung verursachte
kleine ¾nderung der Schallgeschwindigkeit der
SAW als Meûgröûe verwendet. Auch funkabfragbare Sensorik mit SAW ist möglich, so
daû eine direkte Kabelverbindung zwischen
Sensor und Auswerteelektronik entfallen kann.
In der Grundlagenforschung werden SAWunter
anderem zur Untersuchung der dynamischen
Leitfähigkeit von Quantensystemen auf % Halbleitern eingesetzt. Auch hier wird die Wechselwirkung der SAW mit freien Ladungen
(% Elektronen oder % Löcher) in Halbleiterquantenfilmen ausgenutzt. Auf Grund der periodischen Deformation des Substrates durch
eine SAW können diese auch in der % Optoelektronik eingesetzt werden. Hier werden dynamische optische % Gitter zur akustooptischen
Modulation (% akustooptischer Filter) oder
zum Schalten optischer Signale erzeugt. In
jüngster Zeit werden durch die Kombination
von SAW und auch optische Verzögerungsleitungen und Speicher für photonische Signale
diskutiert.
[AW1]
Surface Enhanced Raman Scattering % SERS.
Surfactant, übliche Bezeichnung im englischen
Sprachraum für grenzflächenaktive Substan-
Literatur:
Surfen
236
H
M
1/√χ 2
h
1/√χ (α,β,γ )
MH
1/√χ 1
Suszeptibilitätsellipsoid:
Schnitt durch ein Suszeptibilitätsellipsoid in der H-M-Ebene
für ein magnetisch anisotropes
System.
zen, die das Benetzungs- oder Kristallwachstumsverhalten an Grenzflächen verändern. Im
deutschen Sprachgebrauch steht die Bezeichnung vor allem für Substanzen, die bei Epitaxieprozessen (% Ober- und Grenzflächenphysik, % Molekularstrahlepitaxie) den Ablauf
des Aufwachsprozesses beeinflussen. So kann
z.B. durch eine monoatomare Schicht von As
oder Sb auf Si ein ebenes Aufwachsen dünner
Ge-Schichten erreicht werden, die andernfalls
als Inselchen in der sogenannten StranskiKrastanow-Mode wachsen würden (% Stranski-Krastanow-Wachstum). Der Surfactant
»schwimmt« dabei auf der Ge-Schicht und wird
nicht in den Kristall eingebaut.
Surfen, im Unterschied zum % Segeln eine
Fortbewegungsart, bei der durch das Fehlen
eines Schwertes die Wirkung der Quertriebskraft FQ nicht vernachlässigt werden kann.
Surges, Spitzenprotuberanzen, aktive % Protuberanzen, die aus der % Chromosphäre herausgeschleudert werden (% Flares).
Surveyor, sieben amerikanische Mondsonden
der zweiten Generation, von denen fünf zwischen 1966 und 1968 weich auf dem Erdtrabanten landeten und dabei zahlreiche Fernsehbilder und Informationen zur Erde funkten.
Suspension, eine feine, jedoch nicht molekulare Verteilung eines festen Körpers in einer
Flüssigkeit. Suspensionen sind wie % Emulsionen im Gegensatz zu Lösungen meist optisch
trübe und neigen dazu, sich unter Wirkung der
Schwerkraft in ihre Bestandteile zu zerlegen,
was man durch Zentrifugieren beschleunigen
kann. Im engeren Sinne beschränkt man den
Begriff der Suspension auf Teilchengröûen von
mehr als 10 5 cm. (% Kolloide)
Suspensionspolymerisation,
Polymerisationsverfahren (% Polymerisation), bei dem das
% Monomer durch starkes Rühren in einer nicht
mischbaren Flüssigkeit verteilt und das % Polymer in Perlenform gewonnen wird. Die Polymerperlen werden durch wasserlösliche Suspensionsstabilisatoren (z.B. Gelatine, Stärke)
am Verkleben gehindert.
Suspensionsreaktor, homogener Reaktor, bei
dem der feste Brennstoff (Metall oder Oxid) in
der Moderatorsubstanz zu einer Suspension
aufgeschwemmt ist. Vorteil ist, daû die Spaltprodukte weitgehend in den festen Teilchen
stecken blieben, Nachteil dagegen die zu erwartende Erosion.
SUSY % Supersymmetrie.
Suszeptanz, Blindleitwert, der Imaginärteil des
komplexen Leitwertes Y: B ˆ Im Y ˆ Im(1/Z); Z
ist der komplexe Wechselstromwiderstand
(% komplexe Gröûen in der Elektrotechnik).
Suszeptibilität, im allgemeinen Sinn eine materialspezifische Kenngröûe, die die Reaktion
der Materie auf äuûere Felder beschreibt. Sie
beschreibt die ¾nderung % extensiver Gröûen X,
z.B. des % magnetischen Moments oder der
% elektrischen Polarisation, unter dem Einfluû
entsprechender % intensiver Gröûen Y wie
% magnetischen Feldern B oder % elektrischen
Feldern E,
cX, Y ˆ
qX
,
qY
und heiût entsprechend % magnetische Suszeptibilität oder % elektrische Suszeptibilität. Üblicherweise wird c auf das Volumen oder auf die
Stoffmenge von 1 mol bezogen. Die Suszeptibilität hängt im allgemeinen stark von der Temperatur ab und ist bei magnetischen oder elektrischen Wechselfeldern abhängig von deren Wellenlänge (% komplexe Permeabilität,
% komplexe Dielektrizitätskonstante, % Dispersion). (% verallgemeinerte Suszeptibilitäten)
Suszeptibilitätsellipsoid, Ellipsoid zur graphischen Bestimmung der % magnetischen Suszeptibilität c in anisotropen Materialien
(% Anisotropie, % magnetische Anisotropie) sowie analog der % elektrischen Suszeptibilität.
Die Suszeptibilität ist kein Skalar, sondern ein
% Tensor, so daû der Magnetisierungsvektor
M ˆ m0cH (m0: absolute % Permeabilität) nichtlinear vom magnetischen Feldvektor H abhängt,
d.h. die Magnetisierbarkeit durch die Richtungswinkel a, b, g von H bezüglich der Kristallachsen bestimmt ist. Man definiert deshalb
auch die skalare Suszeptibilität c(a, b, g) mit
Hilfe der Komponente MH ˆ M H=H (H ˆ
jHj) von M in Richtung von H durch MH ˆ m0
c(a, b, g) H. Wählt man das Hauptachsensystem als Koordinatensystem (% Hauptachsentransformation), erhält man die Beziehung
c…a, b, g† ˆ c1 cos2 a ‡ c2 cos2 b ‡ c3 cos2 g,
p
die ein Ellipsoid mit den Hauptachsen 1= c1 ,
p
p
1= c2 und 1= c3 beschreibt. c(a, b, g) ergibt
p
sich aus dem Radius r ˆ 1= c…a, b, g†, der in
Richtung des Magnetfeldes H liegt (siehe Abb.).
Der Magnetisierungsvektor M weist in Richtung
des Nomalenvektors des Ellipsoids und hat den
Betrag
p
m c…a, b, g†jHj
,
jMj ˆ 0
h
wobei h den Abstand der Tangentialebene zum
Mittelpunkt bezeichnet.
Sutherland-Modell, ein Molekülmodell für
reale Gase, welches die Temperaturabhängigkeit
der % Viskosität h(T) unter Berücksichtigung
der Deformierbarkeit der Teilchen bei Zusammenstöûen sowie die zwischenmolekularen
Wechselwirkungskräfte in einer halbempirischen Beziehung, der Sutherland-Gleichung, in
einem
p weiten Temperaturbereich erfaût: h ˆ
B T =…1 ‡ C=T†, (B: Sutherland-Konstante, C:
eine weitere stoffspezifische Konstante).
SU(2), die niedrigste nichttriviale spezielle unitäre Gruppe (% SU(N)) und isomorph zur
Gruppe der Drehungen in einem dreidimensionalen Raum. Ihre niedrigstdimensionale
nichttriviale Darstellung ist durch die zweidimensionalen % Pauli-Matrizen si gegeben,
welche die zugehörige % Lie-Algebra su(2) aufgespannen. Die SU(2) bildet sowohl die % Isospin- und % Spin-Gruppe als auch (in Form der
Untergruppe SU(2) U(1)) die Eichgruppe des
237
% Glashow-Weinberg-Salam-Modells der elektroschwachen Wechselwirkung. (% Darstellung
einer Gruppe)
Sv, Einheitenzeichen für die abgeleitete SI-Einheit % Sievert der % ¾quivalentdosis.
Svedberg, The (Theodor), schwedischer Chemiker, *30.8.1884 Valbo (bei Gävle), ²26.2.1971
Kopparberg (bei Örebro); 1912±49 Professor in
Uppsala; bedeutende Forschungen über Sole,
insbesondere über deren Teilchengröûen; konstruierte Ultrazentrifugen (erreichte mit einer
1926 gebauten Zentrifuge eine Umdrehungszahl
von 40 100 pro Minute) und führte mit diesen
Untersuchungen über Kolloide sowie Proteintrennungen durch; bestimmte die % molekulare
Masse zahlreicher makromolekularer Verbindungen und entwickelte elektrophoretische Methoden, unter anderem zur Trennung von Proteingemischen; entdeckte 1929 das Hämocyanin,
das gröûte damals bekannte organische Molekül;
auch Arbeiten zur Trennung und Herstellung
von Radioisotopen; erhielt 1926 für seine Arbeiten über disperse Systeme den Nobelpreis für
Chemie. Nach ihm ist die Svedberg-Einheit für
den Sedimentationskoeffizienten benannt.
Sverdrup, abgekürzt Sv, nach dem Ozeanographen H.U. Sverdrup benannte Einheit für
den Wassertransport im Ozean. 1 Sv entspricht
1 ´ 106 m3/s.
Sverdrup-Gleichung, von dem Ozeanographen
H.U. Sverdrup 1947 abgeleitete Gleichung zur
Beschreibung der Bewegung von Wassermassen
im Ozean. Sie beruht auf der Erhaltung der potentiellen % Vorticity. Berücksichtigt man nur
die windinduzierte Oberflächen-Schubspannung sowie die Coriolis-Kraft und vernachlässigt die innere Reibung, so ist der totale meridionale Massentransport M proportional zur
Rotation der Schubspannung:
1
M ˆ rotz …t=10 †,
b
wobei t die Oberflächen-Schubspannung und
10 die Dichte ist. Der Proportionalitätsfaktor
b ˆ qf/qy ist die Ableitung des Coriolis-Parameters f ˆ 2Wsinf nach der geographischen
Breite. Die Sverdrup-Gleichung berücksichtigt
neben dem Ekman-Transport (% Ekman-Spirale) auch den geostrophischen Massentranport,
der durch konvergente oder divergente EkmanStrömungen erzeugt wird. Sie beschreibt das
Phänomen, daû die Oberflächenströme auf der
Ostseite der Ozeane erst zum ¾quator und dann
in Richtung Westen abgelenkt werden (% Meeresströmungen).
Sverdrup-Regime, Teil des ozeanischen Strömungssystems, das durch die % Sverdrup-Gleichung beschrieben wird.
Swan-Banden, hauptsächlich in den Spektren
von Kohlenstoffsternen auftretende Banden des
Kohlenstoffradikals C2.
Swapfile, Auslagerungsdatei, virtueller Arbeitsspeicher auf der Festplatte eines Computers, in den Daten und Programmcode aus dem
physikalischen Arbeitsspeicher (% RAM) ausgelagert werden. (% Speicherverwaltung)
symbolische Dynamik
S-Wellen, Sekundärwellen, in der % Seismologie
übliche Bezeichnung für Scherungs- oder
Transversalwellen, die im Vergleich zur Kompressionswelle später ankommt.
s-Wellen-Supraleitung, in der % BCS-Theorie
der einfachste Fall, in dem die % Paarwellenfunktion als Überlagerung ebener s-Wellen angenommen wird. Hierzu muû die Annahme
gemacht werden, daû die attraktive Wechselwirkung translationsinvariant ist und nur vom
Relativabstand der beiden Elektronen abhängt.
Mit r als Relativkoordinate eines Cooper-Paares
nimmt man den Lösungsansatz
X
Y…r† ˆ
Ak eikr :
k
Da diese Funktion symmetrisch ist, die Gesamtwellenfunktion für zwei Elektronen jedoch
antisymmetrisch sein muû, folgt, daû sich die
Elektronenspins bei s-Wellen-Supraleitung
grundsätzlich in % Singulett-Paarung ausrichten. Bei komplizierterer Wechselwirkung
können sich auch Cooper-Paare in % TriplettPaarung ausbilden, die Ortswellenfunktion ist
dann antisymmetrisch (p-Wellen) oder noch
komplexer (d-Wellen in den % Schwerfermionsupraleitern).
swelling, die swell effect, starke Ausdehnung
eines Polymerstrangs während der Verarbeitung. % Polymere erleiden während der Verarbeitung im thermoplastischen oder geschmolzenen Zustand z.T. sehr starke und schnelle
Verformungen, die im molekularen Bereich zu
einer weitgehenden Parallelorientierung der
Kettensegmente führt. Im flüssigen Zustand
können sich die Kettenmoleküle nach der Verformung wieder verknäulen, was bei der Verarbeitung dazu führt, daû ein Polymerstrang,
der das Mundstück einer Spritzdüse verläût, auf
das zwei- bis dreifache anschwillt. Dies ist für
die Herstellung von künstlichen Fasern und
Plastik von groûer Bedeutung.
Swing-by-Technik, Fly-by-Technik, GravityAssist-Technik, Flugführungsverfahren, bei dem
ein Raumflugkörper auf seiner% Freiflugbahn
so weit in die Nähe eines Himmelskörpers gelangt, daû dessen Gravitationswirkung und
Bahngeschwindigkeit zur gewollten Richtungsänderung sowie zur Vergröûerung oder Verringerung der Bahngeschwindigkeit des
Raumflugkörpers relativ zur Sonne ausgenutzt
werden kann.
symbolische Dynamik, Beschreibung eines
durch eine % iterierte Abbildung f gegebenen
% dynamischen Systems mit Hilfe (unendlicher)
Symbolfolgen, für die eine zeitliche Dynamik in
Form einer Abbildungsvorschrift s im Symbolfolgenraum festgelegt wird. Ist die Zuordnung jedes Zustands x des dynamischen Systems (z.B. mittels einer geeigneten Partitionierung des Zustandsraums) zu einer Symbolfolge s durch einen Homöomorphismus gegeben, so sind das gegebene dynamische Systeme und seine symbolische Beschreibung topologisch konjugiert (z.B. das % Smalesche
Hufeisen).
Svedberg, The