Kapitel 8 Supraleitung

Kapitel 8
Supraleitung
8.1
8.1.1
Einleitung
Historische Enwicklung
1911 H. Kamerling Onnes: Entdeckung der Supraleitung in Quecksilber, TC = 4.2 K.
Nobelpreis 1913.
1938 Pyotr Kapitsa: Entdeckung der Suprafluidität in 4 He, TC = 2 K. Nobelpreis 1978.
1950 Vitaly L. Ginzburg und Lev Landau: Phänomenologische Theorie der Supraleitung.
Nobelpreise 1962 für Lev Landau und 2003 für V. Ginzburg.
1957 Alexei A. Abrikosov: Vorhersage von magnetischen Flussschläuchen in Supraleiter.
Nobelpreis 2003.
1957 John Bardeen, Leon Cooper und Robert Schrieffer: Mikroskopische Theorie der
Supraleitung. Nobelpreis 1972.
1962 Brian Josephson: Vorhersage des ‘Josephson Effektes’. Nobelpreis 1973.
1972 D. Lee, D. Osheroff und R. Richardson: Entdeckung der Suprafluidität in 3 He,
TC = 2.7 mK. Nobelpreis 1996.
1972 Anthony J. Leggett: Theorie für die Suprafluidität in 3 He. Nobelpreis 2003.
1986 G. Bednorz und A. Müller, Entdeckung der Hoch-Tc Supraleitung. Nobelpreis 1987.
8.1.2
Makroskopische Elektrodynamik
Die Supraleitung ist ein Phänomen, welche die elekrodynamischen Eigenschaften eines
Festkörpers dramatisch beeinflusst. Wir wiederholen daher kurz die allgemeine Formulierung der Elektrodynamik von Feldern in Festkörpern und verwenden dabei GaussEinheiten.
153
154
KAPITEL 8. SUPRALEITUNG
K
277
000000000000000000000000000000000000000
111111111111111111111111111111111111111
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
Room temperature
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
??
140
120
100
80
60
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
O HgCaBaCuO
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
O TlCaBaCuO
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
O BiCaSrCuO
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
111111111111111111111111111111111111111
000000000000000000000000000000000000000
O YBaCuO
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
111111111111111111111111111111111111111
000000000000000000000000000000000000000
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
Liquid
000000000000000000000000000000000000000
111111111111111111111111111111111111111
000000000000000000000000000000000000000
111111111111111111111111111111111111111
nitrogen
O LaSrCuO
O LaBaCuO
40
20
Liquid
hydrogen
0
O Pb
O Hg
1910
O Nb3Ga
O NbC
O Nb
1930
O Nb3Sn
O NbN
1950
1970
1990
2010
2030
Year
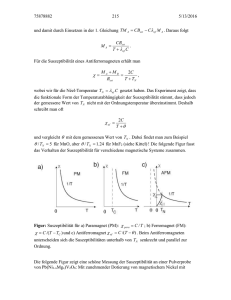
Abbildung 8.1: Historische Entwicklung der Sprung-Temperatur von Supraleiter.
Makroskopische Maxwellgleichungen
Man teilt die Ladungsträger in einem Festkörper in freie (Index f ) und gebundene Anteile
auf und erhält auf diese Weise die makroskopischen Maxwellgleichungen.
• Homogene Gleichungen
∇ · B = 0;
∇×E +
1 ∂B
= 0
c ∂t
∇×H −
4π
1 ∂D
=
jf
c ∂t
c
• Inhomogene Gleichungen
∇ · D = 4πρf ;
• Verknüpfungen
D = E + 4πP;
H = B − 4πM
.
Dabei sind die E und B diejenigen (mikroskopischen) Felder, welche physikalisch via der
Lorentz-Kraft
1
K = q E + v×B
c
auf ein Teilchen mit der Ladung q wirkt.
155
8.1. EINLEITUNG
Superconductor
C (J/mol°K)
S
Cn ∼ γT
C
CS
T
T
c
Abbildung 8.2: Links: Spezifische Wärme im supraleitenden (CS ) und im normal-leitenden
(Cn ) Zustand. Unterhalb der Sprungtemperatur zeigt Cs ein aktiviertes Verhalten, da es
in einem s-Wellen-Supraleiter eine Energielücke gibt.
Rechts: Ein geschlossener Pfad C innerhalb eines Supraleiters und die gerichtete Oberfläche S.
Materialgleichungen
Für die elektrischen Grössen bezeichnet man
• D = ǫE: dielektrische Verschiebung
• P = χe E: dielektrische Polarization
• ǫ = 1 + 4πχe : Dielektrizitäts-Konstante
• χe : dielektrische Suszeptibilität
und analog für die magnetischen Grössen
• H: makroskopisches Magnetfeld, B = µH
• M = χm H: Magnetisierung
• µ = 1 + 4πχm : magnetische Permeabilität
• χm : magnetische Suszeptibilität
Die Abhängigkeit von ǫ und χ, bzw. von χe und χm (welche wir als räumlich isotrop angenommen haben) von den Eigenschaften des Festkörpers nennt man Materialgleichungen.
156
KAPITEL 8. SUPRALEITUNG
Ideal Conductor
Zero-Field Cooled
Field Cooled
T > Tc
T > Tc
B=0
B≠0
T < Tc
B=0
T < Tc
B≠0
T<T
T < Tc
B≠0
B=0
c
Abbildung 8.3: Für einen idealen Leiter macht es (im Gegensatz zu einem Supraleiter!)
einen Unterschied, ob dieser im Feld oder ohne ein äusseres magnetisches Feld gekühlt
wird.
8.1.3
Phasenübergang
Ein eindeutiger Hinweis auf einen Phasenübergang ist dem Verhalten der spezifischen
Wärme zu entnehmen, siehe Fig. 8.2. Der Sprung deutet auf ein Fehlen einer latenten
Wärme hin, also auf einen Phasenübergang zweiter Ordnung. Zudem zeigt die spezifische
Wärme Cs für T < Tc ein aktiviertes Verhalten
Cs ∼ e−β∆ .
(8.1)
Dieses deutet auf eine Energielücke ∆ für thermische Anregungen im supraleitenden Zustand hin.
8.1.4
Meissner-Effekt
Ein Supraleiter verdrängt ein äusseres Magnetfeld vollständig aus dem Supraleiter, wie
Walter Meissner und Robert Ochsenfeld 1933 herausfanden. Im Inneren eines Supraleiters
ist also B = 0. Dieses Phänomen existiert nicht in einem idealen Leiter mit verschwindendem elektrischen Widerstand (ρ = 0). Für diesen gilt nur Ḃ = 0, da das Integral
0 = IR = V =
I
E · dλ =
~ × E · dS = − 1
∇
c
Z S
Z
S
∂B
· dS ,
∂t
(8.2)
157
8.1. EINLEITUNG
χ
Tc
0
Pauli
∝ D(E )
F
T
js
χ
M
∼
∼
∼
∼
H
-1
4π
Abbildung 8.4: Links: Sketch der magnetischen Suszeptibilität eines Supraleiters, der diagmagentische Response ist um Grössenordnungen stärker als die paramagentische PauliSuszeptibilität des Normalleiters.
Rechts: In einem Supraleiter werden spontan Oberflächenströme induziert, welche den
magnetischen Fluss aus dem Inneren des Supraleiters verdrängen.
über jeden geschlossenen Pfad verschwindet. Dabei sind C und S beliebig, also
1
⇒
Ḃ = 0 .
(8.3)
0 = − Ḃ · S
c
Für einen idealen Leiter ist der Widerstand ρ > 0 bei endlichen Temperaturen und das
Magnetfeld dringt ein. Wenn man den idealen Leiter nun in Anwesenheit eines Magnetfeldes abkühlt, dann wird wegen Ḃ = 0 das Magnetfeld auch nicht aktiv verdrängt, im
Gegensatz zum Supraleiter.
Idealer Diamagnetismus
Ein Supraleiter ist ein idealer, thermodynamisch stabiler Diamagnet:
µ−1
B = µH = 0
⇒
µ = 0,
χm =
,
4π
und damit
χSC = −
1
4π
(8.4)
.
Die gemessene Suszeptibilität χ, siehe Fig. 8.4 ist im supraleitenden Zustand also sehr
gross und negativ (diamagnetisch).
Physikalisch rührt der ideale Diamagnetismus von den induzierten Oberflächenströmen
her, welche eine Magnetisierug
1
(8.5)
M = − Hext
4π
im Inneren des Supraleiters aufrecht erhalten. Hierzu wird eine Energie benötigt, welche mit steigendem Hext ansteigt. Ab einem bestimmten Punkt wird der supraleitende
Zustand dann energetisch ungünstig. Es existiert daher ein oberes kritisches Feld Hc .
158
KAPITEL 8. SUPRALEITUNG
H
Normal
Hc
j = j0 e
H
•
(r - r0 )/ΛL
H
⊗
S
r0
j
0
dl
S.C.
Tc
T
Λ
L
Abbildung 8.5: Links: Die Supraleitung wird durch ein starkes äusseres Magnetfeld oder
durch genügend starke thermische Fluktuationen unterdrückt.
Rechts: Ein langer, dicker, supraleitenden Draht. Ein äusseres Feld H dringt nur die
Distanz ΛL ein.
8.2
London-Gleichungen
F. London und H. London haben 1935 eine phänomenologische Theorie entwickelt, welche den Meissner-Effekt erklärt. Sie machten die Annahme, dass es eine Dichte ns von
supraleitenden Elektronen gibt, welche sich ohne Reibung im Metall bewegen können:
∂j
= −ens v̇ .
∂t
mv̇ = −e E,
(8.6)
Damit erhalten wir die erste London-Gleichung
∂js
e2 ns
=
E
∂t
m
.
Wir verwenden nun die Maxwell-Gleichung
~ × E = − 1 ∂B
∇
c ∂t
und erhalten
m ~
∂js 1 ∂B
∂
m ~
1
∇×
+
= 0 =
∇ × js + B
2
2
ns e
∂t
c ∂t
∂t ns e
c
(8.7)
Diese Gleichung beschreibt einen idealen Leiter mit verschwindenem Widerstand ρ = 0).
Um den Meissner-Effekt zu erhalten muss die Klammer identisch verschwinden:
2
~ × js = − ns e B
∇
mc
,
λ =
m
.
ns e2
(8.8)
159
8.2. LONDON-GLEICHUNGEN
x
Bx(z)
1
0.8
SC
0.6
B
y
0.4
j
z
0.2
0
0
1
2
3
z/λL
Abbildung 8.6: Eine supraleitende Halbebene in einem magnetischen Feld parallel zur
Oberfläche. Das äussere Feld dringt bis zu einer Tiefe von λL ein.
Dies ist die zweite London-Gleichung. Die Bedeutung des Parameters λ2 werden wir nun
betrachten.
Feldgleichungen
Wir wollen nun die physikalische Bedeutung der Grösse λ = m/ns e2 herausarbeiten. Beide
London-Gleichungen lassen sich durch λ parametrisieren:
B
~ × js ,
= −λ ∇
c
E = λ
∂js
.
∂t
(8.9)
Diese können wir mit Hilfe der Maxwell-Gleichungen
~ × H = 4π j,
∇
c
gleichzeitig lösen:
~ × B = 4π µ j
∇
c
~ × j = − 4πµ B ,
~ × (∇
~ × B) = 4π µ∇
∇
c
c2 λ
(8.10)
bzw.
~ × B = − 4πµ j .
~ × (∇
~ × j) = − 1 ∇
∇
λc
c2 λ
~ × (∇
~ × a) = ∇(
~ ∇
~ · a) − ∇
~ 2 a und
Mit ∇
~ · B = 0,
∇
(8.11)
~ · j = 1 ∂ρ = 0
∇
c ∂t
(Maxwell und Kontinuitätsgleichung) erhalten wir allgemein
~ 2 B − 4πµ B = 0
∇
c2 λ
Diese beiden Feldgleichungen zeigen uns, dass
Längenskala ist.
~ 2 j − 4πµ j = 0
∇
c2 λ
√
.
(8.12)
λ proportional zu einer charakterischen
160
KAPITEL 8. SUPRALEITUNG
London’sche Eindringtiefe
Wir betrachten nun eine supraleitende Halbebene, wie in Fig. 8.6 illustriert, mit B =
~ × B = 4π µj sind B und j orthogonal, also j = (0, jy (z), 0).
(Bx (z), 0, 0). Wegen ∇
c
Die London-Gleichungen (8.12) werden damit zu
∂ 2 jy
2
− 2 jy = 0 ,
2
∂z
λL
1
∂ 2 Bx
− 2 Bx = 0,
2
∂z
λL
(8.13)
wobei wir mit
s
λL =
c2 λ
=
4πµ
s
mc2
4πns e2 µ
die London’sche Eindringtiefe definiert haben. Die Lösungen fallen im Inneren exponentiell
ab,
Bx = B0x e−z/λL ,
jy = j0y e−z/λL ,
(8.14)
daher die Bezeichung Eindringtiefe.
Kritisches Feld
Wir betrachten nun einen langen, dicken Draht mit Radius r0 ≫ ΛL , wie in der Abb. 8.5
illustriert. Mit Hilfe der Maxwell-Gleichung
~ × H = 4π j
∇
c
(8.15)
finden wir für das Kontour-Integral
~ × H · dS = 4π j · dS .
(8.16)
H · dl =
∇
c
Wir beachten, dass das Magnetfeld nur bis zu einer Tiefe von λL eindringt. Innerhalb
dieser Eindringtiefe sei der mittlere Strom jo :
Z
Z
Z
4π
2πr0 λL j0 .
(8.17)
c
Der supraleitende Zustand kann keine beliebig hohen Ströme unterstützen, es gibt also
eine maximale Stromdichte jc und damit ein kritisches Feld Hc :
2πr0 H =
Hc =
8.3
4π
λL jc
c
.
(8.18)
Cooper-Paare
Die London’sche Theorie beschreibt die Supraleitung phänomenologisch. Sie liefert keine Erklärung für die mikroskopische Ursache der Supraleitung. Um diese zu verstehen
betrachten wir zunächst Wechselwirkung zweier Elektronen im Hintergrund eines FermiSees, das sogn. Cooper Problem.
161
8.3. COOPER-PAARE
e-
+
e-
+
8
vF ∼ 10 cm/s
+
ions
+
region of
positive charge
attracts a second
electron
+
+
+
+
+
+
+
+
+
+
Abbildung 8.7: Illustration: Die negativ geladenen Elektronen an der Fermi-Kante bewegen
sich mit der (hohen) Geschwindigkeit vF durch das Kristall. Die positiv geladenen Ionen
bewegen sich langsam zum vorbeifliegenden Elektron hin und bilden eine leicht erhöhte
Ladungsdichte, welche weitere Elektronen anzieht.
8.3.1
Retardiertes Paarungs-Potential
Im supraleitenden Zustand gibt es eine attraktive Wechselwirkung zwischen Elektronen
auf der Fermi-Fläche, welche zur Bildung von Cooper-Paaren führt. In den normalen
Supraleitern wird die attraktive Elektron-Elektron-Wechselwirkung durch den Austausch
von Phononen erreicht.
Die Deformation des Gitters von Ionen erfolgt auf einer Zeitskala von
τ ∼
2π
∼ 10−13 s
ωD
In dieser Zeitspanne hat ein Leitungselektron den Weg
vF τ ∼ 108
cm
· 10−13 s ∼ 1000A◦
s
zurückgelegt. Ein zweites Elektron kann also retardiert die Anziehung des ersten Elektrons spüren, ohne dass dabei die abstossende Coulomb-Wechselwirkung zwischen den
Elektronen eine Rolle spielt, siehe Fig. 8.7.
8.3.2
Cooper-Instabilität des Fermi-Sees
Wir betrachten nun zwei Elektronen ausserhalb des Fermi-Fläche in Anwesenheit eines
attraktiven Potentials V (r1 , r2 ). Die Schrödinger-Gleichung ist
−
h̄2 ~ 2 ~ 2 ∇ + ∇2 ψ(r1 r2 ) + V (r1 , r2 )ψ(r1 r2 ) = (ǫ + 2EF )ψ(r1 r2 ) .
2m 1
(8.19)
Für ein verschwindendes Potential V = 0 ist die Bindungsenergie ǫ = 0 und die (nicht
symmetrisierte) 2-Teilchen Wellenfunkion ist
ψV =0 (r1 r2 ) =
1 ik1 ·r1 1 −ik2 ·r2
1 ik·(r1 −r2 )
e
e
=
e
,
L3/2
L3/2
L3
(8.20)
162
KAPITEL 8. SUPRALEITUNG
k↑
e
ξ ∼ 1000Α°
e
- k↓
Abbildung 8.8: Die attraktive, Phononen-induzierte Wechselwirkung ist im Ortsraum im
wesentlichen isotrop und Spin-unabhängig. Dieses führt zu einer Paarwellenfunktion, welche als Funktion der Relativ-Koordinate gerade, und im Spin-Sektor ein Singlet ist. Äquivalent hierzu ist eine Paarung von (k, ↑) und (−k, ↓) im Impulsraum.
wobei wir k1 = −k2 = k angenommen haben. Wir nehmen nun an, dass die PaarWellenfunktion ψ(r1 , r2 ) für eine kleine Störung V als Linearkombination der Basisfunktionen (8.20) dargestellt werden kann:
1 X
g(k) eik·(r1−r2 ) .
L3 k
ψ(r1 , r2 ) =
(8.21)
Die k-Summe in (8.21) ist auf einen kleinen Bereich über der Fermi-Schale beschränkt,
mit
EF <
h̄2 k2
< EF + h̄ωD
2m
oder
g(k) = 0
(
für
k <k
qF
k > 2m(EF + h̄ωD )/h̄
(8.22)
(8.23)
da die Debye-Frequenz ωD viel kleiner als die typische Fermi-Energie ist.
Selbstkonsistenz-Gleichung
Eine Fourier-Transformation der Schrödinger-Gleichung ergibt zusammen mit dem Ansatz
(8.21)
h̄2 k 2
1 X
(8.24)
Vk,k′ g(k′ ) = ǫ + 2EF g(k) ,
2
g(k) + 3
2m
L k′
wobei
Vk−k′ =
Z
V (r) e−i(k
−k′ )·r
d3 r
nun die Streuung von Paaren von Elektronen von (k, −k) nach (k′ , −k′ ) beschreibt. Wir
nähern Vk−k′ durch eine attraktive Konstante:
Vk,k′ =
(
−V0
0
2 2
2 ′2
k
< EF + h̄ωD
EF < h̄2mk , h̄2m
sonst.
(8.25)
163
8.3. COOPER-PAARE
Damit wird (8.24) zu
h̄2 k2
V0 X
−
g(k′ ) ≡ −A ,
+ ǫ + 2EF g(k) = − 3
m
L k′
!
(8.26)
bzw.
g(k) =
2 2
− h̄ mk
−A
+ ǫ + 2EF
.
(8.27)
Wir setzen g(k) nun wieder in (8.26) ein und erhalten mit
V0 X
L3 k
A
h̄2 k2
m
− ǫ − 2EF
= +A,
1 =
V0 X
L3 k
1
h̄2 k2
m
(8.28)
− ǫ − 2EF
eine Bestimmungsgleichung für die Bindungsenergie ǫ.
Bindungs-Energie
Wir können die Bestimmungsgleichung (8.28) mit Hilfe der Zustandsdichte N(ω) ≈
N(EF ) pro Spin in ein Integral umwandeln:
1 = V0
Z
EF +h̄ωD
EF
1
ǫ − 2h̄ωD
dE
= V0 N(EF ) ln
N(EF )
2E − ǫ − 2EF
2
ǫ
!
,
(8.29)
mit der Lösung
ǫ =
2h̄ωD
≃ −2h̄ωD e−2/(V0 N (EF )) < 0 ,
1 − e2/(V0 N (EF ))
(8.30)
für V0 /EF → 0. Wir erhalten also einen exponentiell-kleinen Energiegewinn für alle V0 > 0,
welcher nicht-analytisch in V0 ist. Das Resultat (8.30) lässt sich daher nicht in Störungstheorie herleiten.
Instabilität des Fermi-Sees
Aus der Theorie der Potentialstreung wissen wir, dass zwei Teilchen mit einer attraktiven
Wechselwirkung in drei Dimensionen nur dann einen gebungenen Zustand bilden (ǫ < 0),
wenn das Bindungspotential stark genug ist. Für kleine Attraktive Wechselwirkung gibt
es dagegen nur Streuzustände.
Das Resultat von Cooper lehrt uns, dass in Anwesenheit eines Fermi-Sees zwei Elektronen
schon bei einer infinitesimal kleinen attraktiven Wechselwirkung binden. Dabei ist der
Fermi-See passiv. Sein Einfluss ist rein passiv, er beschränkt aufgrund des Pauli-Prinzip
die erlaubten Streuzustände, d.h. das Phasenraumvolumen.
164
8.4
KAPITEL 8. SUPRALEITUNG
BCS-Theorie
Das Cooper-Problem behandelt das Problem von zwei zusätzlichen Elektronen in der
Nähe der Fermi-Kante. Da aber Elektronen ununterscheidbare Teilchen sind, müssen wir
nun eine echte Vielteilchen-Wellenfunktion aufschreiben, für alle Leitungselektronen, welche die Supraleitung beschreibt. Dazu schreiben wir den Hamilton-Operator nochmals in
zweiter Quantisierung auf:
H =
X
ξk c†k,σ ck,σ +
kσ
1 XX
Vq c†k+q,σ c†k′ −q,σ′ ck′ ,σ′ ckσ ,
L3 kk′ q σσ′
(8.31)
mit dem Potential (8.25) und ξk = ǫk − EF . Das Volumen des Kristalls wurde dabei mit
L3 bezeichnet.
BCS-Hamiltonian
Die Supraleitung wird durch die Terme ∼ (−V0 ) mit k′ = −k und σ ′ = −σ im PotentialTerm von (8.31) vermittelt,
HBCS =
X
kσ
V0 X X † †
c c ′ c ′ c .
L3 kp σ p,σ −k ,−σ −k ,−σ kσ
ξk c†k,σ ck,σ −
Dieser Hamilton-Operator wird auch BCS-Hamiltonian genannt, die k-Summationen sind
dabei implizit auf die Fermischale begrenzt.
8.4.1
BCS-Wellenfunktion
Aus dem Cooper-Problem haben wir gelernt, dass Elektronen mit k und −k Paare bilden,
wegen der Symmetrie des Wechselwirkungs-Potentials vorzugsweise mit entgegengesetztem Spin. Die BCS-Wellenfunktion ist daher
|Ψi =
Y
k
uk + vk c†k,↑ c†−k,↓ |0i
,
(8.32)
wobei vk /uk ∼ g(k) einen Zusammenhang mit dem Cooper-Ansatz (8.21) liefert. Die
BCS-Wellenfunktion hat keine feste Teilchenzahl, dafür eine feste Phase.
Die Normierung u2k + vk2 = 1 wird durch die Parametrisierung
u2k
!
ξk
1
1+
,
=
2
Ek
vk2
1
ξk
=
1−
2
Ek
!
(8.33)
erfüllt, wobei sich der zunächst noch freie Parameter Ek später als die Energie der elementaren Anregungen herausstellen wird.
Bogoliubov-Transformation
Wir nehmen erst einmal an, dass (8.32) ein guter Ansatz für den Grundzustand ist. Wie
sehen dann die Anregungen aus? Wir betrachen
c†k,↑|Ψi = uk c†k,↑
Y p6=k
up + vp c†p,↑ c†−p,↓ |0i
(8.34)
165
8.4. BCS-THEORIE
und
c−k,↓ |Ψi = −vk c†k,↑
Y p6=k
up + vp c†p,↑ c†−p,↓ |0i .
(8.35)
Es liegt daher nahe, die Bogoliubov-Transformation
†
γk,↑
= uk c†k,↑ − vk c−k,↓
γ−k,↓ = vk c†k,↑ + uk c−k,↓
(8.36)
zu definieren. Man kann sich leicht überzeugen, dass die γ und γ † antikommutieren.
Bogoliubov Vakuum
Aus (8.34) und (8.35) folgt sofort, dass die γ den BCS-Grundzustand vernichten:
γ−k,↓ |Ψi = 0 ,
und analog für γk,↑ . Die BCS-Wellenfuktion ist also das Vakuum für die Bogoliubov-QuasiTeilchen γ † .
8.4.2
BCS-Theorie für T = 0
Die Bogoliubov-Transformation (8.36) lässt sich invertieren und in den BCS-HamiltonOperator (8.31) einsetzen. Die Rechnung verläuft analog zur Bogoliubov-Transformation,
welche wir zur Berechnung der Dispersionsrelation der Spinwellen in Antiferromagneten
eingesetzt haben, siehe Kap. 6.5.4.
Wir erhalten
H = WBCS +
X
†
Ek γk,σ
γk,σ
,
(8.37)
∆
2Ek
(8.38)
k,σ
mit der BCS-Energie-Relation
Ek =
q
uk vk =
ξk2 + ∆2
für die Bogoliubov-Quasiteilchen, der BCS-Selbstkonsistenz-Gleichung
∆ =
1
1 X
1
q
=
3
V0
2L k ξ 2 + ∆2
k
V0 X
V0 X ∆
u
v
=
,
k
k
L3 k
2L3 k Ek
(8.39)
für die Energielücke ∆ und der BCS-Grundzustands-Energie
WBCS = hψ|HBCS |ψi = 2
= 2
X
k
X
k
2V0 X
ξk vk2 − 3
up vp
L
p
ξk vk2 − uk vk ∆ .
!
X
k
uk vk
!
166
KAPITEL 8. SUPRALEITUNG
1
vk
2
0
kF
k
Abbildung 8.9: Sketch der Paar-Verteilungsfunktion im BCS-Grundzustand. Die gestrichelte Linie ist die lineare Approximation um die Fermi-Energie, der Fermi-See ist gepunktet.
BCS-Grundzustands-Energie
Wir möchten die BCS-Grundzustands-Energie WBCS mit der Energie
X
Wn =
2ξk = 2
X
k
|k|<kF
ξk 1 − θ(ξk )
(8.40)
des Normalleiters und vergleichen. Für eine Abschätzung nähern wir für kleine ∆
vξ2
=







1
2
1−
ξ
∆
1
für ξ < ∆
für ξ ∈ [−∆, ∆]
0 für ξ > ∆
2
Dabei haben wir berücksichtigt, dass v|k=k
= 1/2 und ∂vξ2 /∂ξ = 1/(2∆) an der FermiF
Kante, vergleich Abb. 8.9.
Mit der Zustandsdichte N(EF ) pro Spin and der Fermi-Kante erhalten wir somit
!
ξ
ξ
dξ
1−
− 2N(EF )
2
∆
−∆
WBCS − Wn
≈ 2N(EF )
L3
Z
− 2N(EF )
Z
∆
0
−∆
2
s
∆
ξ2
dξ
1− 2
2
∆
−∆
Z
∆
dξ ξ
∼ −N(EF )∆ .
Der Energiegewinn ist also quadratisch im BCS-Ordnungsparameter ∆, was man durch
eine einfache Reskalierung ξ = ∆x in den Integralen ersieht.
BCS-Zustandsdichte
q
Wir berechnen nun für die Dispersionsrelation Ek = ξk2 + ∆2 der angeregten Zustände
die Zustandsdichte Ns (ω) via
Ns (Ek )dEk = Nn (ξk )dξk .
(8.41)
167
8.4. BCS-THEORIE
sinh x
E
∼ ex
x
Density of additional
electron states only!
∆
1
Ds Dn
Abbildung 8.10: Links: Die BCS-Zustandsdichte.Rechts: Illustration von sinh.
Diese Gleichung drückt die Konstanz der Gesamt-Anzahl der Zustände
aus. In der Nähe
q
2
der Fermi-Kante können wir Nn (ξk ) ≈ Nn (EF ) setzen. Mit Ek = ξk + ∆2 erhalten wir
dann für (8.41) und Ek > ∆
dξx
d q 2
Ek
Ns (Ek )
=
=
.
Ek − ∆2 = q
Nn (EF )
dEk
dEk
Ek2 − ∆2
(8.42)
Für Ek < ∆ gibt es keine Zustände, ∆ ist die Energielücke. Oberhalb von ∆ hat die
Zustands-Dichte eine Divergenz, siehe Fig. 8.10.
BCS-Gap-Gleichung
Wir lösen nun die Bestimmungsgleichung (8.39) für den Ordnungsparameter ∆,
∆ =
V0 X
∆
V0 X ∆
1 V0 X
q
u
v
=
=
.
k
k
3
3
3
2
L k
L k 2Ek
2L k
ξk + ∆2
(8.43)
Wir führen den Kontinuum-Limes durch und beachten, dass bei T = 0 alle Zustände mit
ξ < 0 besetzt sind:
Z
V0 h̄ωD N(EF + ξ)dξ
√ 2
,
(8.44)
1 =
2 −h̄ωD
ξ + ∆2
und erhalten mit
1
=
V0 N(EF )
Z
h̄ωD
0
dξ
h̄ωD
√ 2
= sinh−1
2
∆
ξ +∆
!
(8.45)
die BCS-gap-Gleichung. Für kleine ∆, vergleiche Fig. 8.10, hat (8.45) die Lösung
1
h̄ωD
∼ e V0 N(EF )
∆
1
0 N(EF )
−V
∆ ≃ h̄ωD e
.
(8.46)
Man beachte die bemerkenswerte Ähnlichkeit von (8.46) mit der Lösung (8.30) für die
Bindungsenergie im Cooper-Problem. Bis auf einen Faktor 2 stimmen die Exponenten
überein.
168
KAPITEL 8. SUPRALEITUNG
k′↑
e
kT ∼ 2∆
e
-k′↓
Abbildung 8.11: Um die Cooper-Paare aufzubrechen wird eine Mindestenergie von ∆
benötigt, was für T > 0 durch thermische Anregungen geschehen kann.
8.4.3
Paar-Wellenfunktion
Die Supraleitung ist schlussendlich eine Konsequenz der Paarung von Elektronen. Wir
wollen daher die Eigenschaften der Paar-Wellenfunktion untersuchen.
Groß-kanonische BCS-Wellenfunktion
Die BCS-Wellenfunktion (8.32) hat keine feste Teilchenzahl, lebt also im groß-kanonischem
Ensemble,
|Ψi =
Y
uk +
vk c†k↑ c†−k↓
k
|0i ∼
Y
1+
ak c†k↑ c†−k↓
k
|0i = exp
X
ak c†k↑ c†−k↓
k
!
|0i
wobei ak = vk /uk ist. Dabei ist der letzte Schritt aufgrund der Fermi-Statistik der Elektronen exakt.
Kanonische BCS-Wellenfunktion
Aus der Thermodynamik wissen wir, dass im thermodynamischen Limes die kanonische
und die groß-kanonische Formulierung äquivalent sind. Dies muss auch für die BCSWellenfunktion gelten. Wir definieren mit
PN ,
|ψN i = PN |ψi
einen Projektionsoperator, welcher auf den Unterraum im Fockraum mit fester Teilchenzahl N projiziert, damit hat |ψN i eine feste Teilchenzahl,
|ΨN i ∼
ak c†k↑ c†−k↓
X
k
!N/2
|0i ∼
X
x,y
ax−y c†x↑ c†y↓
!N/2
|0i
(8.47)
und hat die Form einer Bose-Einsteinkondensation von Elektronenpaaren mit der Paarwellefunktion ar , wobei r der relative Abstand der beiden Elektronen ist.
Kohärenzlänge
Der mittlere Abstand ξ der Elektronen, der Radius der Paar-Wellenfunktion, ist durch
ξ
2
=
a2r |r|2
=
P 2
r ar
P
r
P
k
(∇k ak )2
,
2
k ak
P
ak =
vk
vk uk
∆
=
= q
2
uk
uk
ξk2 + ∆2 + ξk
169
8.4. BCS-THEORIE
gegeben. Wir führen nun die Reskalierung
h̄2 kF2 k2
mvF2 2
q =
k̃ ,
=
2m∆ kF2
2∆
k
k̃ =
,
kF
2
∇k̃ =
mvF2
∇q
2∆
durch und erhalten damit
ξ2 ∼
mvF2 1
2∆ kF2
(8.48)
für die typische Ausdehnung eines Cooper-Paars. Diese Länge wird auch Kohärenzlänge
genannt, da sie gleichzeitig die typische Längenskala für die Kohärenz supraleitender Fluktuationen angibt.
Kohärenzlänge und Molekularfeld-Näherung
Typische Werte für die Kohärenzlänge ξ sind
ξ ∼
103 − 104 A◦ .
Ein Cooper-Paar hat in normalen oder typischen Supraleitern daher Kontakt mit
ξ
2
4πn
3
!3
∼ 108
(8.49)
anderen Paaren. Daher ist die Molekularfeld-Näherung der BCS-Theorie i.A. auch sehr
gut.
8.4.4
BCS-Theorie für T > 0
Um die Vorhersagen der BCS-Theorie für T > 0 zu berechnen, müssen wir die T = 0
Gap-Gleichung (8.45) für endliche Temperaturen verallgemeinern.
Gap-Gleichung bei endlichen Temperaturen
Die Wahrscheinlichkeit, ein Elektron im ungepaarten Zustand, also ausserhalb des Kondensats, zu finden ist
1
.
f (Ek + EF , T ) =
exp(βEk ) + 1
Zur Selbstkonsitenz-Gleichung (8.45) tragen jedoch nur die Cooper-Paare bei. Damit haben wir
Z h̄ωD
n
o
dξ
1
√ 2
=
1
−
2f
(E
+
E
,
T
)
(8.50)
k
F
V0 N(EF )
ξ + ∆2
0
q
für T 6= 0. Dabei ist Ek = ξk2 + ∆2 ≥ 0. Für β → ∞ erhalten wir natürlich wieder das
T = 0 Resultat.
Gleichung (8.50) bestimmt ∆(T ), siehe Fig. 8.12.
Bestimmung von Tc
Am Phasen-Übergang, also für T = Tc , verschwindet der Ordnungsparameter, also ∆(T →
Tc −) → 0+ . Damit wird die gap-Gleichung (8.50) zu
1
=
V0 N(EF )
Z
h̄ωD
0
dξ
ξ
tanh
ξ
2kTc
!
,
(8.51)
170
KAPITEL 8. SUPRALEITUNG
In Pb
Sn
∆(T)
∆(0)
Real SC data (reflectivity)
T/Tc
1
Abbildung 8.12: Die Temperatur-Abhängigkeit der Energielücke ∆(T ) im Vergleich mit
experimentellen Daten (aus Relektivitäts-Messungen) und der Vorhersage der BCS-Näherung (8.50).
mit der numerischen Lösung
1 = V0 N(EF ) ln
1.14h̄ωD
,
kTc
kTc = 1.14 h̄ωD e−1/{V0 N (EF )}
.
(8.52)
Wir vergleichen nun Tc mit der Energielücke bei T = 0, ∆ = 2h̄ωD e−1/{V0 N (EF )} , und
erhalten mit
∆(0)
2
=
= 1.764
kTc
1.14
(8.53)
das universelle BCS-Verhältnis, vgl. die Tabelle 8.4.4.
8.4.5
Green-Funktionen
Selbstredend lassen sich Supraleiter auch diagrammatisch beschreiben und dieser Zugang
ist von grosser Bedeutung wenn man kompilierte Situation wie der Eifluss von Unordnung
etc. betrachtet.
Supraleitung entspricht der Paar-Kondensation von Elektronen und spiegelt sich daher in
der Zweiteilchen-Green-Funktion im Teilchen-Teilchen-Kanal (Leiter-Diagramme) wieder.
Metal
Zn
Al
Pb
Tc ◦ K
0.9
1.2
7.22
N(EF )V0
0.18
0.18
0.39
∆(0)/kTc
1.6
1.7
2.15
Tabelle 8.1: Der experimentelle Wert von 2.15 für ∆(0)/kTc ist für Blei grösser als die
BCS-Vorhersage von 1.76. Solche Systeme werden auch stark-Kopplungs-Supraleiter genannt und durch die Eliashberg-Migdal-Theorie beschrieben.
171
8.4. BCS-THEORIE
Hier untersuchen wir die Auswirkungen der Supraleitung auf die Einteilchen-Green-Funktion.
BCS Hamiltonian
Der BCS-Hamiltonian lässt sich entkoppeln,
X
H =
ξk c†k,σ ck,σ
k,σ
X
≈
k,σ
−V
X
c†k′ ,↑ c†−k′ ,↓
k′
ξk c†k,σ ck,σ − ∆∗
X
k
!
X
c−k,↓ ck,↓ − ∆
c−k,↓ ck,↓
k
X
k
!
(8.54)
c†k,↑ c†−k,↓ + |∆|/V ,
mit den molekularen Feldern
∆ = V
X
k′
∆∗ = V
hc−k′ ,↓ ck′ ,↓ i,
X
k′
hc†k′ ,σ ck′ ,σ i .
(8.55)
Normale und anormale Green-Funktion
Wir betrachten nun mit
h
Gk↑ (t) = −iΘ(t)h ck,↑ (t), c†k,↑
i
+
h
Fk↑ (t) = −iΘ(t)h c†−k,↓ (t), c†k,↑
i,
i
+
i
(8.56)
die normale retardierte Green-Funktion Gk↑ (t), sowie den anormalen Anteil Fk↑ (t), vgl.
Kapitel 4.3.
Bewegungsgleichungen
Die Einteilchen-Greenfunktionen gehorchen den Bewegungsgleichungen
h
i
d
Gk↑ (t) = −iδ(t) − Θ(t)h ċk,↑ (t), c†k,↑ i,
+
dt
h
i
d
Fk↑ (t) = −iΘ(t)h ċ†−k,↓ (t), c†k,↑ i ,
+
dt
wobei ċ = i[H, c]− und ċ† = i[H, c† ]− . Analog zum Abs. 4.3.7 finden wir für den BCSHamiltonian (8.54) die Kommutator-Relationen
ċk,↑ = −iξk ck,↑ + i∆ c†−k,↓
ċ†−k,↓ = iξk c†−k,↓ + i∆∗ ck,↑
für die zeitabhängigen Operatoren. Im Frequenzraum wird hieraus
ωGk↑(ω) = 1 + ξk Gk↑ (ω) − ∆Fk↑ (ω)
Fk↑ (ω) = −ξk Fk↑ (ω) − ∆∗ Gk↑ (ω) ,
mit der Lösung
∆∆∗
Gk↑ (ω) = 1,
ω − ξk −
ω + ξk
!
Gk↑ (ω) =
ω2
ω + ξk
.
− ξk2 − |∆|2
Wir finden also mit
Ek =
q
ξk2
+ |∆|2 ,
u2k
!
ξk
1
1+
,
=
2
Ek
vk2
1
ξk
=
1−
2
Ek
!
172
KAPITEL 8. SUPRALEITUNG
die Lösung
Gk↑ (ω) =
u2k
vk2
+
ω − Ek
ω + Ek
,
(8.57)
wie zu erwarten war.
8.5
8.5.1
Anwendungen der BCS-Theorie
Die Energielücke im Experiment
Spezifische Wärme
Die elementare Anregung eines BCS-Supraleiters, die Aufbrechung eines Cooper-Paares,
hat die Energie 2∆. Für kleine Temperaturen hat daher die innere Energie die asymptotische Gestalt
E(T ) ≈ E(T = 0) + 2∆ e−β2∆ ,
T ≪ Tc .
(8.58)
Für die spezifische Wärme finden wir damit
∂E(T ) ∂β
4∆2 −β2∆
C =
≈
e
.
∂β ∂T
T2
(8.59)
Mikrowellen-Absorption und Reflektion
Durch Absorbtions- und Reflexions-Experimente kann der Gap direkt gemessen werden.
Wenn dass einfallende Licht eine Energie h̄ω < 2∆ hat, dann können die Cooper-Paare
nicht aufgebrochen werden und das Licht wird weder reflektiert noch absorbiert. Für
h̄ω = 2∆ ergibt sich eine Resonanz.
8.5.2
Isotopen-Effekt
Die effektive Elektron-Elektron-Anziehung Vk,k′ resultiert aus dem Austausch virtueller
Phononen. Wenn wir die Masse (Isotop) eines der vibrierenden Atome ersetzen, dann
bleiben die elektronischen Eigenschaften des Materials unverändert, insbesondere auch
die Zustandsdichte N(EF ), welche in die BCS-Formel (8.52) für die kritische Temperatur
eingeht. Die Frequenz der Phononen ist dagegen
ωD ∼
s
1
k
∼ M−2 .
M
(8.60)
1
invers proportional zur atomaren Masse und damit auch Tc ∼ M − 2 . Diese Vorhersage
wird durch die meisten “normalen” Supraleiter erfüllt.
173
8.6. SUPRALEITER IM MAGNETFELD
8.5.3
Kritischer Strom und kritisches Feld
Kritisches Feld
Der Energiegewinn (8.41) des supraleitenden Zustandes relativ zum normal-leitenden Zustand,
1
1
N(0)∆2 = 3 (Wn − WBCS ) ,
(8.61)
2
L
muss genügend gross sein, um den Verlust an magnetischer Feldenergie H2 /(8π) auszugleichen. Das klappt bis zu einem kritischen Feld Hc :
1 2
1
N(0)∆2 =
H ,
2
8π c
also
(8.62)
q
Hc = 2∆ πN(0) .
(8.63)
Kritischer Strom
c
Mit Hilfe der London-Gleichungen hatten wir, siehe (8.18), die Beziehung jc = 4πΛ
Hc
L
zwischen dem kritischen Strom jc und dem kritischen Feld Hc hergeleitet. Mit Hilfe von
(8.63) erhalten wir
q
c
2∆ πN(0),
jc =
4πΛL
ΛL =
s
mc2
.
4πne2 µ
(8.64)
Nehmen wir eine konstante Zustandsdichte N(E) ≈ N(0) an, dann ist
N(0) ≃
n
EF
(8.65)
und wir finden mit einer magnetischen Permeabilität µ = 1
c
jc =
4π
s
√
4πne2
πn2m
ne
=
2∆
.
2∆
2 2
2
mc
h̄kF
h̄ kF
s
8.6
Supraleiter im Magnetfeld
8.6.1
Kohärenz und Meissner-Effekt
(8.66)
Der Meissner Effekt ist die zentrale Eigenschaft eines Supraleiters und sollte daher auch
aus der BCS-Theorie ableitbar sein.
Strom-tragende Wellenfunktion
Wir betrachten ein Strom-tragendes Cooper-Paar,
†
ψQ
(r1 , r2) =
1 X
g(k) eiQ·(r1+r2 )/2 eik·(r1 −r2 ) c†k+Q/2,↑ c†−k+Q/2,↓
L3 k
(8.67)
174
KAPITEL 8. SUPRALEITUNG
Normal Metal
SC
φBCS
2
ξ coh > ξ cp
Abbildung 8.13: Links: Innerhalb des Volumens einer Cooper-Paar-Wellenfuktion halten
sich viele Elektronen auf und tragen damit zur Robustheit der Wellenfunktion bei.
Rechts: Der Durchmesser eines Cooper-Paares, ξc wird i.A. kleiner als die Kohärenzlänge
ξcoh sein.
in Analogie zu (8.21) und (8.47). Dabei ist Q die Wellenzahl der Schwerpunkts-Koordinate
R = (r1 + r2 )/2. Insbesondere impliziert (8.67) die Annahme, dass die g(k) unabhängig
vom Impuls h̄ Q des Cooper-Paares sind (Robustheit der Wellenfunktion). Dieses ist nur
dann der Fall, wenn alle anderen Cooper-Paare den selben Impuls haben:
ψQ (r1 , r2 ) = ψQ=0 (r1 , r2 ) eiQ·R .
Robustheit der Wellenfunktion
Wir nehmen nur an, dass alle Cooper-Paare den gleichen Impuls h̄Q haben. Diese Annahme ist in Anbetracht des hohen gegenseitigen Überlapps der Cooper-Paare gerechtfertigt.
Somit ist dann
ΦBCS (Q) = eiϕ ΦBCS (Q = 0) = eiϕ ΦBCS (0) ,
(8.68)
für die Gesamtwellenfunktion ΦBCS in erster Quantisierung, mit der (Gesamt-) Phase
ϕ = Q · (R1 + R2 + ...) .
Supra-Strom
Der Stromoperator für ein einzelnes Cooper-Paar ist
j = −
o
2e n ∗ ∗
ψp ψ + ψ ∗ pψ .
4m
(8.69)
Dieses ist der normale Stromoperator mit der Masse des Paares 2m und der Paar-Ladung
−2e. Aufgrund der Robustheit (8.67) der Paar-Wellenfunktion können wir
~ −
p = −ih̄∇
2e
A,
c
~ = ∇
~R+∇
~r ≈ ∇
~R
∇
(8.70)
175
8.6. SUPRALEITER IM MAGNETFELD
superconducting loop
C
X
X
X
X
X
X
X
B
X
X
X
X
X
X
X
X
X
ΛL
X
Abbildung 8.14: Der magnetische Fluss, welcher einen supraleitenden Ring durchdringt,
ist quantisiert.
setzen. Damit erhalten wir für die Suprastrom-Dichte js :
2e X ∗
~ Rν − 2eA ΦBCS
js ≈
ΦBCS −ih̄∇
4m ν
c
)
∗
2eA
∗
~ Rν −
ΦBCS ,
+ ΦBCS −ih̄∇
c
bzw.
(
X
2e
4eA
~ Rν φ
js = −
|ΦBCS (0)|2
+ 2h̄ |ΦBCS (0)|2
∇
2m
c
ν
)
.
(8.71)
London-Gleichung
~ × ∇φ
~ = 0 für alle φ, und damit wird (8.71) zu
Nun gilt ∇
2
~ × js = − 2e |ΦBCS (0)|2 ∇
~ ×A .
∇
mc
(8.72)
Wenn wir nun mit |ΦBCS (0)|2 = ns /2 die Dichte ns der supraleitenden Elektronen identifizieren, dann erhalten wir die zweite London-Gleichung (8.8):
2
~ × js = − ns e B,
∇
mc
8.6.2
|Φ(0)|2 =
ns
2
.
(8.73)
Magnetische Flussquanten
Die Quanten-Kohärenz der Wellenfunktion eines Supraleiters hat auch zur Folge, dass
der magnetische Fluss von Flussschläuchen quantisiert ist. Wir betrachten den Ausdruck
( 8.71)
eh̄ns X ~
e2 ns
A−
(8.74)
∇Rν φ
js = −
mc
2m ν
176
KAPITEL 8. SUPRALEITUNG
V
a
c
b
V0
metal
d 2ψ
dx 2
+
metal
insulator
0
2m
Eψ = 0
h2
d
2
d ψ + 2m (E - V )ψ
0
h2
dx2
x
d2ψ
2m
+ 2 Eψ = 0
h
dx 2
Abbildung 8.15: Eine Tunnelbarriere zwischen zwei normal-leitenden Metallen.
für den supraleitenden Strom und berechnen das Kontour-Integral
I
e2 ns
js · dl = −
mc
I
I
eh̄ns X ~
A · dl −
∇Rν φ · dl
2m ν
(8.75)
innerhalb des supraleitenden Ringes, siehe Fig. 8.6.1, und weit genug von der Oberfläche
entfernt, so dass kein Magnetfeld mehr vorhanden ist. Demnach ist auch js = 0 entlang
des Kontours und
I
j · dl = 0 .
(8.76)
Eindeutigkeit der Phase
Die Phase φ der Wellenfunktion ΦBCS = eiφ Φ(0) ist eineindeutig, also
XI
ν
~ Rν φ · dl = 2πN,
∇
N ∈Z .
Damit wird das Kontour-Integral (8.75) für den Supra-Strom zu
−
e2 ns Z
eh̄ns
e2 ns I
A · dl = −
B · ds = 2Nπ
,
mc
mc
2m
bzw.
Φ =
Z
B · ds = N
hc
≡ NΦ0
2e
,
(8.77)
mit dem Flussquantum Φ0 = hc/(2e) für den Supraleiter. Wichtig ist hierbei die Ladung
2e im Nenner des Flussquantums. Der totale magnetische Fluss Φ durch den Ring ist also
quantisiert.
8.6.3
Energie eines isolierten Flussschlauchs
Typ-II Supraleiter
In Absch. 8.2 hatten wir gesehen, dass Supraleiter externe Magnetfelder aus ihrem Inneren
177
8.6. SUPRALEITER IM MAGNETFELD
verdrängt, solange die dafür notwendigen diamagnetischen Ströme nicht zu gross sind,
siehe (8.18). Diese Magnetfeld nennt man Hc1
Allerdings bricht die Supraleitung für H > Hc1 nicht notwendigerweise zusammen. Unter bestimmten Umständen ist es für das System energisch güstiger den Supraleitenden
Zustand beizubehalten, dafür aber das Magnetfeld partiell in der Form von quantisierten
Vortizes, auch Flusschläuche genannt, eindringen zu lassen. Man spricht dann vom Typ-II
Supraleiter.
Magnetischer Vortex
Der qualitative Verlauf des Magnetfeldes H(r) und der supraleitenden Wellenfunktion
Ψ(r) ist in Abb. 8.16 für den Fall
λL ≫ ξ
veranschaulicht. Im Kern des Vortex ist normal-leitend, denn hier bricht die Supraleitung
zusammen. Ausserhalb des Kernes dringt das Magnetfeld bis zu einer Tiefe ein, welche
durch die London’sche Eindringtiefe λL gegeben ist.
Magnetisches Fluss eines Vortex
Wir betrachten nun zunächst die magnetische Feldenergie eines Vortex. Die freie LondonGleichung (8.12) hat die Form
~ 2B − 1 B = 0 .
∇
λ2L
Wir nähern nun den Vortex-Kern durch eine δ-Funktion und verallgemeinern die LondonGleichung zu
~ 0 δ(x) ,
B − λ2L ∆B = φ
(8.78)
~ 0 entlang der Vortex-Linie zeigt. Wir integieren über eine Fläche senkrecht zum
wobei φ
Vortex und erhalten
φ0 =
Z
B · d~σ −
λ2L
I
~ × B) · dl ≈
(∇
Z
B · d~σ ,
wenn wir berücksichtigen, dass ein Magnetfeld im Supraleiter nach (8.14) exponentiell
~ × B für r ≫ λL vernachlässigbar ist.
abfällt und damit ∇
Damit ist φ0 nach (8.77) ein Vielfaches des magnetische Flussquantums hc/2e.
Energie eines Vortex
Die Energie eines Vortex setzt sich aus der Feldenergie
EH =
1
8π
Z
d3 x H · B =
µ
8π
Z
d3 x H2
und er kinetischen Energie
mv2
8π c2 (4π)2 m(evns )2
µ
d3 x
ns =
2
8π
µ c2 (4π)2 2e2 ns
!
Z
Z
2
µ
mc2
(4π)2 2
µ
3
2 ~
=
d3 x
d
x
λ
j
n
=
∇
×
H
s
L
s
8π
4πe2 µns
c2
8π
Ekin =
Z
d3 x
Z
178
KAPITEL 8. SUPRALEITUNG
2
|Ψ(r)|
2 λL
2
|H(r)|
2ξ
0
r
Abbildung 8.16: Der Verlauf des Magnetfeldes H(r) = (0, 0, H) und der makroskopischen
√
Wellenfunktion Ψ(r) in einem Vortex als Funktion des Abstandes r = x2 + y 2 in der
x − y Ebene. Entlang der z-Axis ist der Vortex translationsinvariant.
wobei ns die Dichte der supraleitenden Elektronen (nicht der von Cooper-Paaren) ist, und
wir
s
mc2
~ × H = 4π js
,
∇
js = evns ,
λL =
2
4πe µns
c
verwendet haben. Mit (8.78) lässt sich die Energie eines isolierten Vortex damit zu
Ev
µ Z 3
~ ×H 2
d x H2 + λ2L ∇
=
8π
=
φ0
4πλL
!2
log(λL /ξ)
(8.79)
ausrechen.
• Die Energie ist quadratisch im Fluss φ0 . Zwei Flussschläuche mit je einem Fluss φ0
sind daher energetisch günstiger als einer mit Fluss 2φ0 .
• Der Ausdruck (8.79) gilt für eine Flussschlauch mit einem Radius ξ für den normalleitenden Kern. Da die Energie nur sehr schwach, logarithmisch, von der Kohärenzlänge
ξ abhängt, ist dieses eine vertretbare Approximation.
8.6.4
Untere kritische Feld Hc1
Wir kommen nun auf die Eingangs gestellte Frage zurück: Wann ist es energetisch günstig
wenn einzelne Flussschläuche in den Supraleiter eindringen?
Energiebilanz
Mit einer Querschnittsfläche πξ 2 für den normalleitenden Kern ergibt sich die Energiebilanz zu
!
πξ 2
H
Ev
∆E = Ev −
−
.
(8.80)
B · H = φ0
4π
φ0
4π
179
8.6. SUPRALEITER IM MAGNETFELD
Dabei ist der zweite Term die magnetische Feldenergie des normalleitenden Kernes, welche
man gewinnt. Zudem haben wir
πξ 2 B = φ0 =
hc
2e
verwendet. Die Energiebilanz wird für
Hc1 =
4πEv
=
φ0
φ0
log(λL /ξ)
4πλ2L
(8.81)
negativ.
Hc1 ≪ Hc ,
q
Hc = 2∆ πN(0) .
Typ I und Typ II Supraleiter
Wenn wir (8.47) benutzen, und die Zustandsdichte N(0) durch kF parametrisieren erhalten
wir
Hc1
π ξ
= √
log(λL /ξ)
Hc
24 λL
(8.82)
für das Verhältnis Hc1/Hc .
Für die meisten Supraleiter ist die Kohärenzlänge ξ in der Grössenordnung von einigen
zehn Angström und die Eindringtiefe λL in der Grössenordnung von einigen tausend
Angström. Damit ist i.A. Hc1 deutlich kleiner als das thermodynamische kritische Feld
(8.63). In diesem Fall spricht man von Typ-II Supraleiter, ansonsten von Typ-I Supraleiter.
Typ-II Supraleiter
Wenn das Magnetfeld in den Supraleiter in der Form von Flussschläuchen eindringen
kann, dass bricht die Supraleitung auch nicht für H > Hc zusammen, sondern erst bei
einem höheren Feld, welches Hc2 genannt wird, vgl. Abb. 8.17.
8.6.5
Magnetische Flussgitter
Im vorangehenden Abschnitt haben wir die Eigenschaften einzelner Flussschläuche für
den Fall H > Hc1 mit H ≃ Hc1 betrachtet. Im allgemeinen müssen wir jedoch für
Hc1 < H < Hc2
damit rechnen, dass es eine endliche Dichte von Vortizes gibt und diese miteinander wechselwirken.
Abrikosov Gitter
In der gemischen oder Meisner-Ochsenfeld-Phases eines Typ-II Supraleiters ordnen sich
180
KAPITEL 8. SUPRALEITUNG
Typ −I
−M
Typ −II
H
H
c1
Hc
H c2
Abbildung 8.17: Die Magnetisierungs-Kurven für Typ-I und Typ-II supraleiter.
die magnetischen Flusslinien zu einem Gitter an, dem Abrikosov-Gitter. Die Flusschläuche
haben eine repulsive Wechselwirkung und das Gitter ist ein Dreiecksgitter.
Hochtemperatur-Supraleitern
Die Hochtemperatur-Supraleitern sind ausgesprochene Typ-II Supraleiter, ξ ist in der
Grössenordnung von wenigen Angström.
Die kritische Temperatur Tc ist in den Hochtemperatur-Supraleitern ist so hoch, dass das
Abrikosov-Gitter aufgrund termischer Anregungen schmelzen kann. Es kommt zu einem
Phasenübergang fest-flüssig für die Flusslinien.
Supraleitung und Dissipation
Typ-II Supraleitung haben weiterhin einen verschwindenden elektrischen Wiederstand,
solang sich die Flussschläuche nicht bewegen können. Diese ist im Abrikosov-Gitter der
Fall, denn das Gitter als Ganzes ist starr.
Dissipation, und damit ein endlicher elektrischer Wiederstand, tritt auf sobald sich die
Flussschläuche zu bewegen beginnen, denn die Vortizes haben ja einen normalleitenden
Kern.
Daher versucht man in technischen Anwendungen Verunreinigungen gezielt in die Supraleiter einzubringen, an welchen die Flusslinien festgehalten werden (gepinnt).
8.7
8.7.1
Tunnel-Kontakte
Tunneln in einen Supraleiter
Wir betrachten als Einführung den Tunnelkontakt zwischen zwei normal-leitenden Metallen, siehe Fig. 8.15, z.B. durch eine dünne Oxidschicht.
Potentialbarriere
Die von links einfallende Wellenfunktion ψa trifft auf die Tunnelbarriere, ψb , und propagiert dann nach rechts weiter, ψc :
ψa = A1 eikx + B1 e−ik·x
′
′
ψb = A2 eik ·x + B2 e−ik ·x
ψc = B3 e−ik·x .
(8.83)
181
8.7. TUNNEL-KONTAKTE
S
N
I
E
eV
X
N(E)
Abbildung 8.18: Illustration eines Tunnelkontaktes zwischen einem Normal-Leiter und
einem Supraleiter in der Anwesenheit einer angelegten Spannung V .
Mit diesem Ansatz ist die Schrödinger-Gleichung zu lösen, falls
√
2mE
k =
in a & c
q h̄
2m(E − V0 )
k′ =
in b
h̄
(8.84)
(8.85)
Die Koeffizienten A1, 2 und B1,2,3 werden durch die Stetigkeitsbedingungen für ψ, ψ ′ und
x = 0,x = d bestimmt. Für E < V0 , also für
q
k ′ = iκ =
2m(E − V0 )/h̄
(8.86)
finden wir für die Tunnelwahrscheinlichkeit
Pl→r

1
|B1 |2
1
=
=
−
2
2
|B1 |
8
k κ
−
κ k
!2
1
+
8
k κ
+
κ k
!2
cosh 2κd
−1

.
(8.87)

Für grosse Werte von κd vereinfacht sich die Tunnelwahrscheinlichkeit zu
Pl→r
k κ
∝ 8
+
κ k
!−2
k κ
+
= 8
κ k
!−2
e−2κd


exp −

(8.88)
q

2d 2m(V0 − E) 
h̄
.
(8.89)

Die Wahrscheinlichkeit durch die Potentialbarriere zu tunneln fällt also exponentiell ab.
N-S Kontakt
Wir betrachten nun die Tunnelrate für einen N-S Kontakt, also die Injektion von Elektronen aus einem Normalleiter in einen Supraleiter, siehe Fig. 8.18, bei einer angelegten
Spannung V .
Sei f (ǫ) die Fermi-Verteilungsfunktion und Nn (ǫ) und Ns (ǫ) die jeweiligen Zustandsdichten des normal- bzw. des supreleitenden Kontaktes.
182
KAPITEL 8. SUPRALEITUNG
dI
dV
I
∆/e
∆/e
V
V
Abbildung 8.19: Bei tiefen Temperaturen sind N-S Tunnel Kontakte sehr gut geeignet um,
via der differentiellen Leitfähigkeit, die quasi-Teilchen Zustandsdichte im Supraleiter zu
messen.
Der Tunnelstrom ist mit
I ∝ P
− P
Z
Z
dǫ f (ǫ − eV )Nn (EF ) Ns (ǫ)(1 − f (ǫ))
dǫ f (ǫ)Ns (ǫ) Nn (EF )(1 − f (ǫ − eV ))
proportional zur Differenz der Tunnelwahrscheinlichkeiten P (n → s) und P (s → n). Ohne
eine äussere Spannung (eV = 0) verschwindet der Tunnelstrom (I = 0).
Differentieller Tunnelstrom
Sei nun eV > 0 und kT ≪ ∆. Wegen der Energielücke in Ns (ǫ) ist P (s → n) unterdrückt
und
Z
I ∼ P Nn (EF ) dǫ f (ǫ − eV )Ns (ǫ) .
Der differenzielle Tunnelstrom
dI
∼ P Nn (EF )
dV
Z
dǫ
∂f (ǫ − eV )
Ns (ǫ)
∂V
nimmt daher für tiefe Temperaturen,
∂f
∼ eδ(ǫ − eV − EF ),
∂V
(T ≪ EF )
die Form
dI
≃ P Nn (EF )Ns (eV + EF )
dV
(8.90)
dI
an. Mit dV
lässt sich also die Zustandsdichte Ns (ǫ) im Supraleiter als Funktion der angelegten Spannung V direkt messen, vgl. Fig. 8.19.
183
8.7. TUNNEL-KONTAKTE
8.7.2
Josephson-Effekt
In Abs. 8.7.1 haben wir das Tunneln von einzelnen Elektronen von einem Normaleiter
in einen Supraleiter betrachtet. Es stellt sich nun die Frage, ob bei Kontakt von zwei
Supraleiter auch das Tunneln von Cooperpaaren möglich ist, und welche Auswirkungen
ein solcher Tunnelprozess hat.
Phänomenologischer Wellenfunktion
Nach (8.68) und (8.73) schreiben wir
Ψ = ΦBCS =
q
ns /2 eiϕ = |Ψ| eiϕ
für die supraleitende Wellenfunktion, wobei ns die Dichte von Cooper-Paaren ist, und ϕ
die Phase.
Phänomenologische Schrödingergleichung
Für zwei Supraleiter Ψ1 und Ψ2 im Kontakt gilt demnach die phänomenologische Schrödingergleichung
∂
Ψ1 = E1 Ψ1 + KΨ2
ih̄ ∂t
(8.91)
∂
ih̄ ∂t
Ψ2 = E2 Ψ2 + KΨ1
wobei E1/2 die jeweiligen Grundzustands-Energien sind und K die (Paartunnel-) Kopplungskonstante.
Tunnelstrom von Cooper-Paaren
Der Strom I1→2 von tunnelnden Cooper-Paaren ist durch
∂ 2
∂Ψ∗
∂Ψ1
I1→2 = e Ψ1 = eΨ∗1
+ e 1 Ψ1
(8.92)
∂t
∂t
∂t
e
E1 |Ψ1 |2 + KΨ∗1 Ψ2 − E1 |Ψ1 |2 − KΨ∗2 Ψ1
=
ih̄
eK ∗
eK
=
Ψ1 Ψ2 − Ψ∗2 Ψ1 =
|Ψ1 ||Ψ2| ei(ϕ2 −ϕ1 ) − ei(ϕ1 −ϕ2 )
ih̄
ih̄
2eK
|Ψ1 ||Ψ2 | sin(ϕ2 − ϕ1 )
=
h̄
gegeben. Wir erhalten also einen Gleichstrom von Cooper-Paaren wann immer eine Phasendifferenz ∆ϕ zwichen den beiden Supraleitern existiert.
Gleichstrom Josephson Effekt
Um die zeitabhängigkeit der Phasendifferent in (8.92) zu berechnen, trennen wir Realund Imaginärteil in der die makroskopische Schrödinger-Gleichung (8.91),
∂
|ψ1 | − h̄ϕ̇1 = E1 |ψ1 | + K|ψ2 |ei(ϕ2 −ϕ1 )
∂t
∂
ih̄ |ψ2 | − h̄ϕ̇2 = E2 |ψ2 | + K|ψ1 |ei(ϕ1 −ϕ2 )
∂t
ih̄
was uns zu
E1
K |ψ2 |
−
cos(ϕ2 − ϕ1 )
h̄
h̄ |ψ1 |
K |ψ1 |
E2
−
cos(ϕ1 − ϕ2 )
= −
h̄
h̄ |ψ2 |
ϕ̇1 = −
ϕ̇2
184
KAPITEL 8. SUPRALEITUNG
führt. Für näherngsweise gleiche Dichte von Cooper-Paaren |Ψ1 |2 = |Ψ2 |2 in den beiden
Supraleitern erhalten wir damit
ϕ̇1 − ϕ̇2 =
E2 − E1
eU
≡
,
h̄
h̄
ϕ1 − ϕ2 =
eU
t.
h̄
(8.93)
Dabei haben wir eine angelegte Spannung von U angenommen, welche ja den respektiven
Nullpunkt der Energieskalen um eU verschiebt. Damit erhalten wir mit
eU
eK
ns sin
t
I =
h̄
h̄
(8.94)
einen (hochfrequent-) oszillierenden Strom bei anlegen einer Gleichspannung, der (Gleichspannungs) Josephson-Effekt.
SQUIDS
Der Josephon-Effekt ist auch die Grundlage für eine ganze Reihe von Anwendungen,
insbesondere für die SQUIDS, den ‘Superconducting Quantum Interference Devices’. Ein
SQUID besteht aus einem supraleitenden Ring, der an einer oder zwei Stellen durch
Josephson-Kontakte unterbrochen ist. Zusammen mit der in Abschn. 8.6.2 besprochenen
Flussquantisierung im Ring erlaubt das SQUID hochpräzise Magnetfeld-Messungen.