Vorlesung Geoinformatik I
Werbung

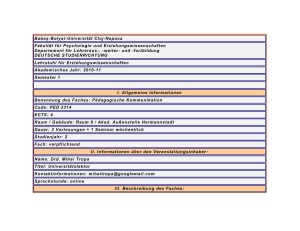
Fakultät Forst, Geo- und Hydrowissenschaften, Fachrichtung Geowissenschaften, Professur Geoinformationssysteme
Vorlesung
Geoinformatik I
0. Einige Grundbegriffe & Grundlagen
Lars Bernard
Überblick
Einige mathematische Grundlagen
der Geoinformatik
Mengentheoretische Grundbegriffe
Grundbegriffe der formalen Logik
Grundbegriffe der Graphentheorie
Einige informatorische Grundlagen der Geoinformatik
Grundlegende Begriffe
Aufbau und Funktionsweise von Computern
Für Nicht-Mathematiker und Nicht-Informatiker…
Vorlesung Geoinformatik I – Lars Bernard
2
Mengentheoretische Grundbegriffe - Wozu?
z.B. für alle Operationen und Algorithmen auf
Daten“mengen“
etwa für die relationale Algebra,
die wiederum Grundlage der Abfragesprachen für
(relationale) Datenbanken ist…
Abfrage in SQL:
SELECT HName, HAdresse,
HTelefon, STyp
FROM
Sensoren, Hersteller
WHERE Sensoren.HName =
Hersteller.HName
AND
Zustand = 'defekt'
Vorlesung Geoinformatik I – Lars Bernard
3
Mengentheoretische Grundbegriffe
Unter einer Menge A versteht man eine
Zusammenfassung von bestimmten wohl
unterschiedenen Objekten unserer Anschauung oder
unseres Denkens zu einem Ganzen; diese Objekte
werden Elemente a der Menge A genannt.
Schreibweise:
a∈A
"a ist Element der Menge A"
b∉A
"b ist nicht Element der Menge A"
Vorlesung Geoinformatik I – Lars Bernard
4
Mengentheoretische Grundbegriffe
Die Festlegung einer Menge A kann erfolgen
explizit durch Angabe aller Elemente, z.B. M = {a, b,..., z};
dies ist nur bei einer endlich grossen Menge möglich.
implizit durch Angabe eines Prädikates, d.h. einer
charakteristischen Eigenschaft aller Elemente dieser Menge,
z.B.:
M = { x | x ∈ Z und x > 0; Z = Menge der ganzen Zahlen }
Die Anzahl M der Elemente einer Menge M heißt
Kardinalität von M.
Vorlesung Geoinformatik I – Lars Bernard
5
Mengentheoretische Grundbegriffe
Beziehungen zwischen Mengen
Gleichheit:
A = B ⇔ jedes Element von A ist Element von B und umgekehrt;
anderenfalls ist A ≠ B
Teilmenge
A ⊆ B ⇔ (x ∈ A ⇒ x ∈ B) für alle x ∈ A
A ⊂ B ⇔ A ⊆ B und A ≠ B (echte Teilmenge)
Transitivität:
A ⊆ B und B ⊆ C ⇒ A ⊆ C
Vorlesung Geoinformatik I – Lars Bernard
6
Mengentheoretische Grundbegriffe
Spezielle Mengen:
Leere Menge
∅ = { x ⏐ x ≠ x }, auch: { }
Potenzmenge
P(A) = { X ⏐ X ⊆ A }
Menge aller möglichen Teilmengen von A
Beispiel: A={1,2} → P(A)={∅, {1}, {2}, {1,2}}
Produktmenge
(Kartesisches
Produkt):
A × B := {(x,y) ⏐ x ∈ A und y ∈ B}
Menge aller geordneten
(Koordinaten-)Tupel (x, y)
Allgemein: A×B×C usw.
Speziell: A×A×A ... ×A := An
z.B. R3 dreidimensionale reeller Zahlenraum
Vorlesung Geoinformatik I – Lars Bernard
7
Mengentheoretische Grundbegriffe
Mengenalgebraische Verknüpfungen:
Durchschnitt
A ∩ B = { x ⏐ x ∈ A und x ∈ B}
A und B sind disjunkt,
wenn A ∩ B = ∅
Vereinigung
A∪B=
{ x ⏐ x ∈ A oder (auch) x ∈ B}
Differenzmenge
A \ B = { x ⏐ x ∈ A und x ∉ B}
"A ohne B"
Vorlesung Geoinformatik I – Lars Bernard
8
Mengentheoretische Grundbegriffe
Einige Gesetze der Mengenalgebra (etwa zur
Vereinfachung komplexer Ausdrücke)
Kommutativität
A ∩ B = B ∩ A (gilt ebenso für ∪)
Assoziativität
(A ∩ B) ∩ C = A ∩ (B ∩ C)
(gilt ebenso für ∪)
Distributivität
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Vorlesung Geoinformatik I – Lars Bernard
9
Mengentheoretische Grundbegriffe
Relationen
Eine mittels bestimmter Eigenschaften definierte
Teilmenge R ⊆ X×Y der Produktmenge X ×Y heißt eine
zweistellige (binäre) Relation R zwischen den beiden
Mengen X und Y.
Statt (x,y) ∈ R schreibt man auch: xRy
Analog definiert man n-stellige Relationen.
Vorlesung Geoinformatik I – Lars Bernard
10
Mengentheoretische Grundbegriffe
Relationen
Beispiel 1:
"<" ist eine binäre Relation im R2: (x,y) ∈ "<" bzw. x < y
Beispiel 2:
"liegt zwischen" =
{ (a, b, c) ⏐a, b, c ∈ G und c ist ein Punkt auf der Geraden g(a, b)}
ist eine dreistellige Relation R ⊆ G×G×G für Punkte
eines 2-dim. Gebietes G.
Vorlesung Geoinformatik I – Lars Bernard
11
Mengentheoretische Grundbegriffe
Eigenschaften von Relationen:
Reflexiv
xRx
z.B. ist "≤" reflexiv
Symmetrisch
aRb ↔ bRa
z.B. ist "=" symmetrisch
Antisymmetrisch aRb und bRa → a = b
Transitiv:
aRb und bRc → aRc
z.B. ist "≤„ antisymmetrisch
z.B. ist "<" transitiv
R heißt Äquivalenzrelation,
wenn R reflexiv, symmetrisch und transitiv ist.
Die Menge der Elemente, die in Äquivalenzrelation
zueinander stehen, bilden eine Äquivalenzklasse
R[x] = { y ⏐ (x,y) ∈ R}. .
Mittels Äquivalenzrelationen können also Partitionen
(Klasseneinteilungen) in einer Menge gebildet werden.
Vorlesung Geoinformatik I – Lars Bernard
12
Mengentheoretische Grundbegriffe
Äquivalenzrelationen
Beispiel:
"parallel" ist eine Äquivalenzrelation in der
Menge aller Geraden einer Ebene; damit
können Klassen paralleler Geraden
gebildet werden.
Ordnungsrelationen
R heisst eine Ordnungsrelation, wenn R reflexiv,
antisymmetrisch und transitiv ist (z.B. ≤).
Ordnungsrelationen sind z.B. für das grössenmässige Sortieren
von Daten wichtig.
Vorlesung Geoinformatik I – Lars Bernard
13
Wozu?
Grundbegriffe der formalen Logik
z.B. für alle Arten der Verknüpfung von Daten
Etwa für Analysen der Art:
mein Haus soll nah an der S-Bahn und ruhig gelegen sein
oder einen großen Garten haben…
Reduzierung der Aussagemöglichkeiten auf wahr oder falsch
erleichtert bzw. erlaubt die automatisierte Verarbeitung und
Analyse und ist methodische Basis heutiger Rechnerchips
Vorlesung Geoinformatik I – Lars Bernard
14
Grundbegriffe der formalen Logik
Unter einer Aussage versteht man ein
natürlichsprachiges Konstrukt, dem man einen der
beiden Wahrheitswerte WAHR (W) oder FALSCH (F)
zuordnen kann.
Die Bewertung erfolgt nach dem Prinzip tertium non datur
(entweder W oder F).
fuzzy logic ist eine Verallgemeinerung dieser zweiwertigen
Logik.
Beispiele:
1. "Die Lufttemperatur liegt unterhalb von Null Grad Celsius"
ist eine Aussage, die W oder F sein kann
2. "Regnet es immer noch?" ist keine Aussage.
Vorlesung Geoinformatik I – Lars Bernard
15
Grundbegriffe der formalen Logik
Aussageform:
Enthält ein sprachliches Konstrukt anstelle eines konkreten
Subjektes nur eine Variable, so handelt es sich um eine
Aussageform
Beispiel:
"X < 0 °C" ist eine Aussageform
Wird X an ein konkretes Subjekt gebunden,
entsteht eine wahre/falsche Aussage:
"Die Lufttemperatur ist < 0 °C" kann W oder F sein.
Tautologie:
Aussageformen, die bei jeder Bindung der Variablen eine wahre
Aussage ergeben
Beispiel:
"X < 0°C oder X > 0°C oder X = 0 °C"
Vorlesung Geoinformatik I – Lars Bernard
16
Grundbegriffe der formalen Logik
Verknüpfung von Aussagen
Umgangssprachlich und, oder, wenn…dann
Formal: Wenige, eindeutig definierte Junktoren (Wahrheitstafeln)
Vorlesung Geoinformatik I – Lars Bernard
17
Grundbegriffe der formalen Logik
Beispiel:
Die Subjunktion "ein Viereck ist
rund" → "5 < 2" ergibt eine
wahre Aussage
…nach dem formal-logischen
Prinzip "ex falso quod libet" !...
Formeln der Aussagenalgebra
Komplexe Aussageformen, die durch Verknüpfung mehrerer
Aussageformen entstanden sind
Beispiel: (A ∧ B) → (A ∨ B)
übrigens eine Tautologie…
Vorlesung Geoinformatik I – Lars Bernard
18
Grundbegriffe der formalen Logik
Schlussregeln
Mittels sogenannter Schlussregeln lassen sich wahre Aussagen
bzw. Aussageformen (also Tautologien) in andere
Aussageformen umwandeln.
So lassen sich komplexe logische Formeln vereinfachen.
Mit den de Morgan‘schen Regeln kann weiterhin jede Formel so
reduziert werden, dass nur die Verknüpfungen UND, ODER und
NICHT (∧, ∨, ¬ ) benötigt werden!
…letztlich kann so jede Aussageform in eine (elektronische)
logische Schaltung abgebildet werden (Halbleiter)…
Vorlesung Geoinformatik I – Lars Bernard
19
Grundbegriffe der formalen Logik
Beispiel einer praktischen Implementierung: Volladdierer
Binärdarstellung
22
21
20
1
0
1
5
1
1
01
1
5
1
0
1
0
10
23
a=
b=
a+b =
Dezimal
Beachte:
0+0=0
0+1=1+0=1
1+1=0 mit Übertrag
1
Allgemein:
Übertrag an Stelle i: Üi; Summe an Stelle i: S;
Ü1 = A0 ∧ B0 S0 = (A0 ≠ B0)
Ü[i+1] = (Ai ∧ Bi) ∨ (Ai ≠ Bi) ∧ Üi (i = 1, . . . n-1)
Si = (Ai ≠ Bi ≠ Üi) (i = 1, . . . n-1)
Vorlesung Geoinformatik I – Lars Bernard
20
Wozu?
Grundbegriffe der Graphentheorie
Für alle Analysen von Nachbarschaftsbeziehungen (Topologie)
Etwa Streckenberechung in Netzen
Konsistenzbestimmungen
Aber auch Datenstrukturierung (Bäume)…
Vorlesung Geoinformatik I – Lars Bernard
21
Grundbegriffe der Graphentheorie
Ein Graph besteht aus Kanten (Abk. e von edge) und
Knoten (Abk. v von vertex), wobei eine Kante durch zwei
Knoten gebildet wird
Zwei Knoten heißen adjazent (benachbart), wenn sie zu
einer gemeinsamen Kante gehören; diese beiden Knoten
heißen dann inzident zur betreffenden Kante.
Vorlesung Geoinformatik I – Lars Bernard
22
Grundbegriffe der Graphentheorie
Beispiel:
Graph G = (V, E) mit
V = {v1, v2, v3} und
E = {e1, e2, e3}
wobei
e1 = (v1, v2);
e2 = (v2, v3);
e3 = (v3, v1)
Adjazenzliste zur einfachen „Speicherung“ eines Graphen:
Für Graph mit n Knoten ist dies eine Liste aus n Elementen;
Jedes Element ist eine knotenspezifische Liste,
die einen Knoten und alle seine Nachbarknoten aufführt.
Hier: { [v1, v2, v3], [v2, v3, v1], [v3, v1, v2] }
…natürlich hoch-redundant
Vorlesung Geoinformatik I – Lars Bernard
23
Grundbegriffe der Graphentheorie
Spezielle Graphen
In einem zusammenhängenden Graph
existiert für je zwei verschiedene Knoten
x und y stets ein Weg von x nach y.
- Ein Weg von x (Anfangsknoten) nach
y (Endknoten) ist eine nicht-leere,
endliche Liste von paarweise
adjazenten Kanten.
In einem gerichteten Graph bestehen
alle Kanten aus geordneten KnotenPaaren (= Vorgänger-Knoten und
Nachfolger-Knoten).
Vorlesung Geoinformatik I – Lars Bernard
24
Grundbegriffe der Graphentheorie
Spezielle Graphen
Ein Graph, bei dem alle Knotenpaare
adjazent sind, heißt ein vollständiger Graph
und ist ausschließlich zyklisch (…etwa
Kataster).
Die Zyklen bilden Maschen/Flächen
f (engl. faces).
Masche f
planar
nicht planar
Die (isomorphe) Abbildung planarer Graphen
in der 2D-Ebene hat ausschließlich Knoten
als Schnittpunkte von Kanten
In planaren Graphen gilt der
Eulersche Satz (Konsistenzbestimmung):
V+F = E +S
mit Anzahl Knoten V, Maschen F,
Kanten E und zusammenhängenden Teilen S
Vorlesung Geoinformatik I – Lars Bernard
V=3
F=1
E=3
S=1
25
Grundbegriffe der Graphentheorie
Spezielle Graphen – Bäume:
Ein Baum ist ein zusammenhängender,
schleifenloser, gerichteter Graph (...Fluss).
Ein Wurzelbaum ist ein Baum, der genau
einen Knoten ohne Vorgänger-Knoten besitzt
(Wurzel).
Alle anderen Knoten besitzen genau einen
Vorgänger-Knoten ('Vater').
Knoten ohne Nachfolger-Knoten ('Sohn')
heißen Blatt (…wichtig etwa für
Datenstrukturen).
In einem Binärbaum, hat jeder Knoten
höchstens zwei Söhne (linker & rechter Sohn;
…wichtig etwa für die Suche).
Vereinfachung des Eulerschen Satz:
E=V-1
Vorlesung Geoinformatik I – Lars Bernard
26
Überblick
Einige mathematische Grundlagen
der Geoinformatik
Mengentheoretische Grundbegriffe
Grundbegriffe der formalen Logik
Grundbegriffe der Graphentheorie
Einige informatorische Grundlagen der Geoinformatik
Grundlegende Begriffe
Aufbau und Funktionsweise von Computern
Für Nicht-Mathematiker und Nicht-Informatiker…
Vorlesung Geoinformatik I – Lars Bernard
27
Aufbau und Funktionsweise von Computern
Der Prozessor führt die
Anweisungen des
Programms aus.
Der Hauptspeicher
enthält das
auszuführende
Maschinenprogramm
und nimmt die Daten auf.
Der I/O-Controller (E/AKanal) führt die
Kommunikation mit der
Umwelt (Peripherie) des
Computers durch.
Das Bussystem stellt die
Verbindungen zwischen
diesen Komponenten her.
Vorlesung Geoinformatik I – Lars Bernard
28
Aufbau und Funktionsweise von Computern
Charakteristika von Prozessoren
Taktfrequenz:
- Häufigkeit des Wechsels der Schaltzustände
im Prozessor pro Sekunde;
- je höher desto schneller ist der Prozessor;
Maßeinheiten = MHz, GHz (MegaHerz, GigaHerz)
Internes Datenformat:
- Anzahl der Bit die in einer Takteinheit gleichzeitig verarbeitet werden können
(je breiter desto schneller)
Externes Datenformat:
- Anzahl der Bit, die in einer Takteinheit zwischen Prozessor und
Hauptspeicher ausgetauscht werden können; ("Datenbus - Breite„)
Physikalischer Adressraum:
- Anzahl der Speicherzellen, die für Programm, Daten und Systemsoftware
maximal adressierbar, also mit Daten belegbar sind; Maßeinheit MB/GB;
Maximale Rechenleistung:
- Theoretisch auf Grund der Taktfrequenz und der Datenformate erreichbare
Rechenleistung,
- Einheit MIPS = million instructions per second
Vorlesung Geoinformatik I – Lars Bernard
29
Aufbau und Funktionsweise von Computern
Charakteristika des Hauptspeichers
(Arbeitsspeicher)
ROM:
- Read Only Memory
- Beim Startvorgang (boot)
wird aus dem ROM (Lese-Speicher) zunächst ein Kernprogramm in
den Arbeitsspeicher geladen. Dies lädt dann maschinenspezifische
Daten und einen Teil des Betriebssystems in den Arbeitsspeicher.
RAM:
- RAM-Speicher (Random Access Memory)
Der eigentliche Hauptspeicher mit Schreib- und Lese-Zugriff
Cache
- Spezieller Puffer-Hauptspecher zwischen
dem Prozessor und dem eigentlichen Hauptspeicher
- enthält jeweils die am häufigsten benutzten Daten,
Befehle oder Adressen
Vorlesung Geoinformatik I – Lars Bernard
30
Aufbau und Funktionsweise von Computern
Charakteristika des I/O-Controller
Kommunikation
-
über Hardware-Schnittstellen (Ports) und
Software-Schnittstellen (Treiber):
Beispiele für Standards für Hardware-Schnittstellen bei PCs:
1. Serielle Schnittstelle (auch: V24 oder COM)
– alter, langsamer jedoch recht einfacher Standard; in IndustriePeripheriegeräten immer noch sehr verbreitet (Sensoren!)
2. Parallele Schnittstelle (auch: Centronics oder LPT):
-
Ebenfalls älterer Standard, Datenwerden parallel übertragen
3. Universal Serial Bus (USB)
-
Neuerer Schnittstellentyp, mit sehr schnellen Datenübertragung
Erlaubt hot-link: jeweiliges Peripheriegerät kann bei laufendem Rechner
angeschlossen werden, der jeweilige Gerätetreiber wird automatisch
erkannt
4. FireWire-Schnittstelle (IEEE 1394, i.link):
-
Neuerer Schnittstellentyp mit extrem schneller Datenübertragung, (Audiound Videodaten, externer Festplattenlaufwerke)
Vorlesung Geoinformatik I – Lars Bernard
31
Aufbau und Funktionsweise von Computern
Bus-System
stellt die Verbindungswege zwischen
den Funktionseinheiten des Computers her.
Funktioniert nach dem Prinzip einer
Sammelleitung
Es werden Datenbus, Adressbus und
Kontrollbus unterschieden
Vorlesung Geoinformatik I – Lars Bernard
32
Aufbau und Funktionsweise von Computern
Externe Speicher
Magnetplatten (Festplatten)
- Magnetisches Speicher-Medium
bestehend aus übereinander angeordneten
rotierenden Platten mit Schreib-/Leseköpfen.
- Erlauben schnellen Zugriff und werden als Fest- oder Wechselplatten
genutzt; gezieltes Lesen und Schreiben von Dateien.
- Meist genutzt zur Daten-Bearbeitung
CD-ROM, DVD
- Ähnlich der Audio-CD (Lasertechnik); Kapazität 650 MB bei CD-R/RW;
relativ langsam; DVDs sind CD-ähnliche Medien mit sehr hoher
Speicherkapazität (4,7 GB bei DVD-R/RW)
- Meist genutzt zur Datenarchivierung
USB Sticks
- Wiederbeschreibbare Flash-Speicher
die über den USB Port angeschlossen werden
- Meist genutzt zum Daten-Austausch
…
Vorlesung Geoinformatik I – Lars Bernard
33
Aufbau und Funktionsweise von Computern
Betriebssystem bündelt
Basis-Schnittstelle zum Anwender
(Betriebssystem-Kommandos)
Manipulation von Daten und Dateien
(z.B. Kopieren, Löschen)
Ansteuerung von Peripherie-Geräten
(Tastatur, Monitor, Disketten, Festplatten, Drucker)
(Aktuelle) Beispiele
Windows (Microsoft):
Leistungsfähiges 32bit-Betriebssystem für PC und Workstations; in mehreren
Varianten für Clients und Server verfügbar (z.B. Windows XP)
UNIX (ULTRIX/DEC, Solaris/SUN, HP-UNIX…) :
Betriebssystem für leistungsfähige Rechner (Workstations);
leichte Vernetzbarkeit, gute Sicherungsmöglichkeiten gegen unerlaubten Zugriff;
relativ kompliziert in der Wartung; diverse, nicht immer kompatible UNIX-Derivate
LINUX (Open Source):
Als Alternative zu UNIX von einer internationalen Entwicklergemeinschaft im
Internet entwickelt; praktisch kostenlos; großer Pool kostenfreier Software
verfügbar
Vorlesung Geoinformatik I – Lars Bernard
34
Aufbau und Funktionsweise von Computern
‚Gesetz‘ von Moore (1970/65):
Anzahl an Transistoren auf einem handelsüblichen Prozessor
verdoppelt sich ca. alle achtzehn Monate
Quelle: http://de.wikipedia.org/wiki/Mooresches_Gesetz
Vorlesung Geoinformatik I – Lars Bernard
35
Literatur und Referenzen…
Umfassende (Schul-)Formelsammlung
Bartelme, N. (2000): Geoinformatik – Modelle,
Strukturen, Funktionen.
Bill, R. (1999): Grundlagen der Geoinformationssysteme.
Band 1 & 2. Heidelberg, Wichman.
Worboys, M. F. (1995). GIS - A Computing Perspective.
London, Taylor & Francis.
Vorlesung Geoinformatik I – Lars Bernard
36