ω ω ω α - Uni Kassel
Werbung
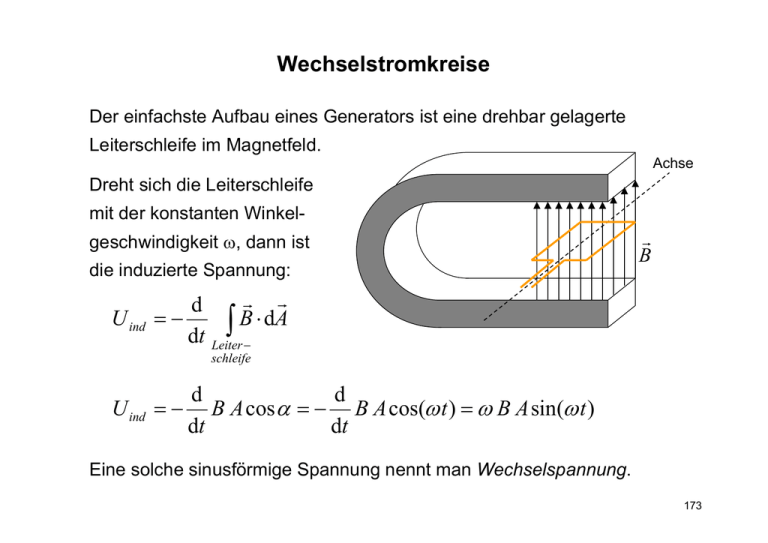
Wechselstromkreise Der einfachste Aufbau eines Generators ist eine drehbar gelagerte Leiterschleife im Magnetfeld. Achse Dreht sich die Leiterschleife mit der konstanten Winkelgeschwindigkeit ω, dann ist die induzierte Spannung: U ind r B r r d =− B ⋅ dA ∫ dt Leiter − schleife U ind = − d d B A cos α = − B A cos(ω t ) = ω B A sin(ω t ) dt dt Eine solche sinusförmige Spannung nennt man Wechselspannung. 173 Im allgemeinen Fall schreibt man U = U 0 cos(ω t + ϕ ) Die Wechselspannung hat die Amplitude U0, und die Frequenz f = Den Winkel ϕ bezeichnet man als Phase. ω 2π U (t ) U0 t T Die grüne Kurve hat 90° = π/2 rad Phasenverschiebung gegenüber der schwarzen Kurve. Die Periodendauer T beträgt T = 1/ f = 2π ω 174 Effektivspannung Der Effektivwert Ueff wird so definiert, das eine Wechselspannung an einem ohmschen Widerstand R die gleiche mittlere Leistung erzeugt, wie eine Gleichspannung mit U=Ueff. U0 cos(ω t ) R 2 T 2 2 U U 1 U 1 U0 eff P = 0 ∫ cos 2 (ω t ) dt = = ⇒ U eff = 0 R T 0 R 2 R 2 P = U (t ) I (t ) = U 0 cos(ω t ) P(t ) U eff U (t ) Peff Wechselspannung Gleichspannung 175 Netzspannung Zur Versorgung der Haushalte wird Wechselspannung mit Ueff = 220V verwendet. Es stehen drei „Phasen“ zur Verfügung, die jeweils eine um 120° phasenverschobene Wechselspannung gegenüber dem „Nullleiter“ besitzen (Drehstrom). U (t ) U0 U eff t Die Amplitude beträgt 220V·√2 = 311 V Zwischen unterschiedlichen Phasen misst man eine noch höhere Spannung, sie beträgt bis zu 540 V = 220V·√6 . Die Effektivspannung zwischen zwei Phasen beträgt 380V = 220V·√3 . 176 Wechselstromkreis mit Spule Eine Induktivität (Spule) führt in einem Wechselstromkreis zu einer Phasenverschiebung zwischen Strom und Spannung. Beim Einschalten einer Spule hatten wir gesehen, das nach Anlegen der Spannung der Strom linear ansteigt I U (t ) t I entsprechend zum Einschalten I t U 177 Annahme: Spule ohne ohmschen Widerstand Der Strom steigt so schnell mit der Zeit an, dass die angelegte Spannung gleich der induzierten Gegenspannung ist. Die Kirchhoffsche Maschenregel fordert: U (t ) + U ind = 0 dI U 0 cos(ωt ) − L = 0 dt U (t ) U ind Durch Integration ergibt sich I= U0 U0 U0 cos( ω ) d = sin( ω ) = cos(ωt + 90°) t t t ∫ ωL ωL L Der Strom ist gegenüber der Spannung um 90° phasenverschoben. Die Spule verhält sich nicht als ohmscher Widerstand, d.h. der Strom ist nicht zu jeder Zeit proportional zur Spannung. 178 Komplexer Widerstand einer Spule Die Effektivwerte von Strom und Spannung sind proportional zueinander U eff I eff = U0 =ωL I0 Um die Phasenverschiebung zu berücksichtigen und in Wechselstromkreisen mit Widerständen rechnen zu können, führt man den komplexen Widerstand ein. Z = iω L Im komplexe Zahlenebene ωL 90° R Re Mit reellem ohmschen Widerstand und imaginärem Widerstand der Spule erhält man einen Winkel von 90° zwischen beiden. 179 Wechselstromkreis mit Kondensator Die Spannung am Kondensator ist proportional zur Ladung und steigt bei konstantem Strom linear an: U= U Q It = C C U (t ) t entsprechend zum Laden des Kondensators U t I 180 Annahme: Stromkreis mit Kondensator ohne ohmschen Widerstand Es gilt: Q(t ) = CU (t ) Mit der Spannung → I (t ) = dQ dU =C dt dt U (t ) = U 0 cos(ωt ) folgt I (t ) = −ω CU 0 sin(ωt ) = ω CU 0 cos(ωt − 90°) Der Strom ist gegenüber der Spannung auch um 90° phasenverschoben, aber zeitlich in die andere Richtung. Die Effektivwerte von Strom und Spannung sind proportional zueinander U eff I eff = U0 1 = I0 ω C 181 Komplexer Widerstand eines Kondensators Um die Phasenverschiebung richtig zu berücksichtigen wird dem Kondensator der komplexen Widerstand 1 1 = Z = −i ω C iω C zugeordnet. Im komplexe Zahlenebene 1 −i ωC 90° R Re 182 Wechselstromkreis mit Spule, Kondensator und Widerstand Nach der Kirchhoffschen Maschenregel gilt: U (t ) + U ind = U R + U C U ind Es folgt U (t ) − L dI Q = I R+ dt C UC U (t ) Ein weiteres Differenzieren liefert UR dU d2I dI 1 =L 2 +R + I dt dt dt C Mit der äußeren Spannung U (t ) = U 0 cos(ωt ) I (t ) erhalten wir die Differentialgleichung für den Strom d2I dI 1 ω U 0 sin(ω t ) = L 2 + R + I dt dt C 183 Die Differentialgleichung ähnelt sehr der Dgl. für erzwungene Schwingungen aus der Mechanik. Lösung durch Ansatz mit komplexer e-Funktion: Verwenden wir für die äußere Spannung die Funktion U (t ) = U 0 e iωt = U 0 cos(ωt ) + i U 0 sin(ωt ) Erhält man als Dgl. i ω U 0 e iω t d2I dI 1 =L 2 +R + I dt dt C Die Lösung dieser inhomogenen Dgl. ist die Summe aus der Lösung der homogenen Dgl. und einer speziellen Lösung der inhomogenen Dgl. Die Lösung der homogenen Dgl. (d.h. ohne äußere Spannung) ist exponentiell gedämpft und spielt nach einer Weile keine Rolle mehr. Als Ansatz für eine spezielle Lösung verwenden wir eine Funktion, die die selbe Frequenz wie die äußere Spannung besitzt. 184 Mit dem Ansatz I (t ) = I 0 ei (ωt −ϕ ) ergibt sich durch Einsetzen in die Dgl: iω U 0 e iωt = − Lω 2 I 0 e i (ωt −ϕ ) + i Rω I 0 ei (ωt −ϕ ) + 1 I 0 e i (ωt −ϕ ) C Umformen ergibt: 1 ⎞ ⎛ i U 0 e i ωt = I 0 e iω t e − i ϕ ⎜ − L ω + i R + ⎟ ωC ⎠ ⎝ i ⎞ ⎛ U 0 = I 0 e − iϕ ⎜ i L ω + R − ⎟ ωC ⎠ ⎝ Man drückt jetzt den Zusammenhang zwischen den Scheitelwerten von Strom und Spannung mit einem komplexen Widerstand Z der s.g. Impedanz aus. U 0 = Z I 0′ 185 In der Konstanten I 0′ ist die Phasenverschiebung um den Phasenwinkel ϕ enthalten U 0 = Z I 0′ = Z I 0 e − iϕ Es ergibt sich also für die Impedanz Z: i Z = i Lω + R − ωC Für den Betrag von Z erhält man Im (Re Z ) + (Im Z ) 2 1 ⎞ ⎛ = R + ⎜ Lω − ⎟ ω C ⎝ ⎠ 2 2 |Z | Z = 2 Den Phasenwinkel berechnet man aus Im Z = arctan ϕ = arctan Re Z Lω − 1 ωC Lω − 1 ωC ϕ R Re R 186 Schein-, Wirk-, und Blindwiderstand Die Impedanz bezeichnet man auch als Scheinwiderstand. Den Ohmschen Widerstand R, d.h. den Realteil von Z nennt man Wirkwiderstand. Den Imaginärteil der Impedanz nennt man Blindwiderstand. Die Darstellung der Impedanz als Pfeile in der komplexen Zahlenebene nennt man Zeigerdiagramm. Im Die Impedanzen in einer Schaltung ohmschen Widerstände im reellen Fall. |Z | addieren sich (komplex) wie die Lω − 1 ωC ϕ R Re 187 Elektrische Leistung beim Wechselstrom Man muss zwischen Blindleistung und Wirkleistung unterscheiden. In einem Wechselstromkreis ohne ohmschen Widerstand wird keine Energie in Wärme umgesetzt. Die von Spule und Kondensator aufgenommene Energie wird im Feld gespeichert und bei der folgenden Halbwelle wieder abgegeben. Im zeitlichen Mittel wird daher keine Leistung aufgenommen (Blindleistung). Die tatsächlich „verbrauchte“ (in andere Energieformen umgewandelte) Leistung ist die Wirkleistung: T T U I U I 1 Pel = ∫ U (t ) I (t ) dt = 0 0 ∫ cos(ω t ) cos(ω t + ϕ ) dt = 0 0 cos ϕ T 0 T 0 2 Bei Spule und Kondensator ist die Phasenverschiebung ϕ zwischen Strom und Spannung gerade ± 90° (cos ϕ = 0) und daher die Wirkleistung gleich Null. 188 Hochpass-Filter Einen Hochpass-Filter passieren die hohen Frequenzen, während die tiefen Frequenzen unterdrückt werden. Man kann die Reihenschaltung von Kondensator und Widerstand als Spannungsteiler auffassen. Ue Ua Am Ausgang Ua liegt also nur ein Bruchteil der Eingangsspannung Ue an: Ua = ZR R Ue = Ue i Z ges R− ωC Nach kurzer Rechnung erhält man für Betrag und Phase Ua = ω RC 1+ ω R C 2 2 2 Ue 1 ϕ =arctan ω RC 189 Frequenzabhängigkeit: Ua Ue = 1 Ua Ue = 1 2 ω= 1 RC ω= 1 RC ω RC ϕ = 90° ϕ = 45° ω RC 190 Tiefpass-Filter Einen Tiefpass-Filter passieren die tiefen Frequenzen, während die hohen Frequenzen unterdrückt werden. Man kann die Reihenschaltung von Kondensator und Widerstand wieder als Spannungsteiler auffassen. Ue Ua i ZC 1 ω C Ue = Ue Ua = Ue = i 1 + iω R C Z ges R− ωC − Nach kurzer Rechnung erhält man für Betrag und Phase Ua = 1 1+ ω R C 2 2 2 Ue ϕ =arctan(− ω R C ) 191 Frequenzabhängigkeit: Ua Ue = 1 Ua Ue = 1 2 ω= 1 RC ω= 1 RC ω RC ϕ = 0° ϕ = −45° ϕ = −90° ω RC 192 Frequenzfilter (Bandpass) Aus Widerstand, Kondensator und Spule kann eine Filter für einen schmalen Frequenzbereich aufgebaut werden. Anwendung: Abstimmung auf einen Radiosender Die Reihenschaltung erzeugt eine Spannung am Widerstand von Ua = Ue Ua ZR R Ue = Ue i Z ges R + iω L − ωC Nach kurzer Rechnung erhält man für Betrag und Phase Ua = ( R R + ωL − 2 ) 1 2 ωC Ue ϕ =arctan 1 ωC − ωL R 193 Frequenzabhängigkeit: Ua Ue = 1 Δω = ω =1 LC ω =1 LC R L ω LC ϕ = 90° ϕ = 0° ϕ = −90° ω LC 194 Elektrischer Schwingkreis Schaltungen aus Widerstand, Kondensator und Spule verhalten sich analog zu mechanischen Schwingungen. Die äußere Wechselspannung entspricht der Anregung bei der erzwungenen Schwingung. Die Energie oszilliert zwischen elektrischer Feldenergie im Kondensator und magnetischer Feldenergie in der Spule. Der ohmsche Widerstand verursacht Dissipation: (Erzeugung von Wärme) analog zur Reibung in der Mechanik. Die Schwingungsdauer der ungedämpften Schwingung ist T = 2π LC Es tritt Resonanz auf, wenn die anregende Frequenz nahe der Eigenfrequenz der Schwingung liegt (vgl. Bandpass-Filter). Bei der Resonanzfrequenz „springt“ die Phase um 180°. 195 Transformatoren In der Technik sind Transformatoren weit verbreitet. Zur Übertragung von elektrischer Leistung über weite Strecken ist Hochspannung erforderlich, für elektronische Anwendungen muss auf wenige Volt reduziert werden. r B An der Primärspule liegt die Wechselspannung U1 = U 0 cos(ωt ) U1 U2 die einen Strom I1 bewirkt: U 0 cos(ωt ) = L dI1 dΦ = N1 dt dt Die selbe Flussänderung dΦ/dt geschieht in der Sekundärwicklung, da alle magnetischen Feldlinien durch beide Spulen verlaufen. 196 Dadurch wird in der Sekundärwicklung die Spannung U ind = − N 2 dΦ dt induziert. Als Spannungsverhältnis ergibt sich U 1 dΦ U = =− 2 N 1 dt N2 ⇒ U2 N =− 2 U1 N1 Beide Spannungen sind um 180° gegeneinander phasenverschoben. Der Strom dI 1 U 0 = cos(ωt ) L dt ⇒ U0 I1 = sin(ωt ) L hat eine Phasenverschiebung von 90 Grad gegenüber der Spannung. Der unbelastete Transformator nimmt daher keine Leistung auf. (Durch den ohmschen Widerstand der Spule und Verluste bei der Ummagnetisierung des Eisenkerns wird dennoch Leistung aufgenommen.) 197 Wird an die Sekundärspule ein Verbraucher angeschlossen, fließt auch dort ein Strom ( I2 ). Dieser Strom ist um 90° phasenverschoben gegenüber dem Strom I1 und erzeugt eine zusätzliche Flussänderung dΦ2/dt. Durch die Phasenverschiebung beider magnetischer Flussänderungen ergibt sich eine Phasenverschiebung von Strom gegenüber Spannung im Primärkreis ungleich 90°. Dies führt zu einer Leistungsaufnahme im Primärkreis. Die aufgenommene Leistung wird im Sekundärkreis wieder abgegeben. Im Transformator treten ohmsche Verluste auf. Zusätzlich treten Verluste bei der Ummagnetisierung des Eisenkerns auf (Fläche der Hystereseschleife). Im Eisenkern induzierte Wirbelströme verursachen auch Verluste. Der Kern wird aus dünnen, gegeneinander isolierten Blechen aufgebaut, die die Ausbildung großräumiger Wirbelströme unterbrechen. 198 Tesla-Trafo Mit einer Primärwicklung aus sehr wenigen Windungen und einer Sekundärwicklung aus vielen tausend Windungen bei gleichzeitig hohen Spannungen und Frequenzen können sehr große Spannungen erzeugt werden. 199 Induktionsofen Wenn die Spannung hochtransformiert wird, wird der maximal entnehmbare Strom auf der Sekundärseite entsprechend kleiner. Die maximal entnehmbare Leistung ist ≤ der abgegebenen Leistung an der Primärseite. Transformiert man die Spannung herunter, können auf der Sekundärseite sehr hohe Ströme fließen. r B → Elektrisches Schweißen → Induktionsofen U1 200











