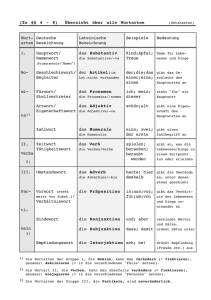
Verbandstheorie

Verbandstheorie
Skriptum zur Vorlesung im Sommersemester 2011
Thomas Vetterlein
Institut für Wissensbasierte Mathematische Systeme
Johannes-Kepler-Universität Linz
Altenberger Straße 69
4040 Linz, Österreich
[email protected]
Zusammenfassung
Wir geben einen Überblick über die Theorie der Verbände. Es handelt sich um eine
algebraische Struktur, die in vielen Bereichen der Mathematik auftaucht, ja mit
deren Hilfe man viele Teile der Mathematik begründen kann. Unser Schwerpunkt
liegt auf der Logik sowie auf der Geometrie.
Inhaltsverzeichnis
1 Einleitung
3
2 Distributive Verbände
5
2.1
Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.2
Posets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.3
Verbände . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
2.4
Distributive Verbände . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.5
Darstellungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . .
26
2.6
Logik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
29
3 Boolesche Algebren
36
3.1
Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
3.2
Komplemente in Verbänden . . . . . . . . . . . . . . . . . . . . . . .
37
3.3
Boolesche Algebren . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
3.4
Darstellungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
3.5
Logik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
1
4 Äquivalenzrelationen und Partitionsverbände
46
4.1
Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
4.2
Partitionsverbände . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.3
Darstellungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
5 Modulare Verbände
54
5.1
Motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
54
5.2
Modulare und lineare Verbände . . . . . . . . . . . . . . . . . . . . .
55
5.3
Atomistische Verbände . . . . . . . . . . . . . . . . . . . . . . . . .
59
5.4
Projektive Geometrien . . . . . . . . . . . . . . . . . . . . . . . . .
64
5.5
Darstellungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
2
1 Einleitung
Verbandstheorie – ist das etwas Abgehobenes? Zu den Zielen dieser Vorlesung gehört
es, das Gegenteil zu demonstrieren. Wenn man will, kann man im Gegenteil den Begriff
des Verbandes als etwas eher Banales ansehen.
In der Tat basiert der Begriff auf recht schlichten Überlegungen. Man gehe von einer Menge aus, deren Elemente irgendeine Art von Information repräsentieren. Wenn
man von inhaltlichen Aspekten einmal absieht, bleibt immer noch eines, was die innere
Struktur einer solchen Menge kennzeichnet: die relative Aussagekraft. Eine Information kann mehr aussagen als eine andere, d.h. letztere in ersterer enthalten sein. Durch
diese Beziehung wird die Menge, wie es heißt, partiell geordnet. Setzt man nun voraus, daß mit je zwei Informationsstücken auch deren gemeinsamer Durchschnitt sowie
deren Vereinigung vorliegt, gelangen wir zum Begriff des Verbandes.
Die Definition mag schlicht sein; sie führt zu einer Theorie, die es in sich hat. Verbandstheorie ist ein umfangreiches Gebiet der Algebra und betrifft nicht nur die letztere; Bezüge bestehen zur Logik und zur linearen Algebra (in Abgrenzung zur abstrakten
Algebra so bezeichnet) und damit auch zu Geometrie und Analysis.
Was die Theorie aber so faszinierend macht, ist der Umstand, daß Verbände in den genannten Bereichen nicht einfach nur irgendwie auftauchen; dies träfe auf wohl fast alle
Gebiete der Mathematik zu. Vielmehr ist es in vielen Gebieten möglich, mit Verbänden
gewissen Typs zu beginnen und zu derjenigen Struktur zu gelangen, die in der jeweiligen Theorie im Mittelpunkt steht.
Paradebeispiel sind die linearen Räume. Man kann den Rn als Menge von n-Tupeln
reeller Zahlen verstehen und reelle Zahlen ihrerseits als Ergebnis eines nichttrivialen Konstruktionsprozesses. Man kann lineare Räume, und nicht nur solche über R,
aber auch durch die inneren Eigenschaften ihrer Unterräume charakterisieren. Die Unterräume bilden einen Verband; die verwendete Beziehung zwischen Unterräumen ist
schlicht die, ineinander enthalten zu sein. Projektive Geometrie ist hier das Stichwort,
deren Anwendungen bis zu den Grundlagen der Quantenphysik reichen.
Ablauf der Vorlesung
Abschnitt 2 behandelt distributive Verbände, die sich durch Systeme von Teilmengen
realisieren lassen. Wir fügen im nachfolgenden Abschnitt 3 eine Komplementfunktion
hinzu und gelangen zu booleschen Algebren. Abschnitt 4 hat eine Brückenfunktion zu
dem, was anschließend folgt. Wir wenden uns der Theorie der Äquivalenzrelationen
zu; denn diese bietet sozusagen einen Schirm für die Theorie der Verbände, und zwar
ohne jede einschränkende Bedingung. Verbände und Unterverbände von Äquivalenzrelationen zerfallen in drei Gruppen; der sogenannte Typ 3 (und höher) umfaßt (in zu
präzisierendem Sinn) alle Verbände, Typ 2 die modularen und der Typ 1 die linearen.
Die modularen und noch mehr die linearen Verbände, die in Kapitel 5 besprochen werden, sind von eminentem geometrischem Interesse. Hier ist die projektive Geometrie
einzuordnen, hier ergeben sich die Verbindungen zur linearen Algebra.
3
Wenn eine neue Sorte Verbände eingeführt wird, gehen wir immer nach dem folgenden
Schema vor. Wir betrachten erstens ein prototypisches Beispiel; mit diesem wird die
Anwendung der Theorie spezifiert und ermöglicht, sich manchen reichlich abstrakten
Begriff konkret vorstellen zu können. Wir entwickeln zweitens die jeweilige Darstellungstheorie; das bedeutet zu zeigen, daß sich die betrachtete, abstrakt definierte Klasse
von Verbänden mit einer gewissen Klasse von Beispielen exakt deckt. Und drittens geht
es um die Frage, wie man hinsichtlich der betrachteten Verbände Schlüsse ziehen kann,
was also daraus gefolgert werden kann, daß zwischen gewissen Elementen eines Verbandes gewisse Beziehungen bestehen. Das bedeutet, eine zugehörige Logik anzugeben, sofern eine solche existiert. Im Fall der booleschen Algebren ist dies die klassische
Aussagenlogik, ansonsten ergeben sich speziellere oder allgemeinere Schlußsysteme.
4
2 Distributive Verbände
2.1 Motivation
Befassen wir uns zunächst mit den Grundlagen mathematischer Modellierung. Wie
entsteht ein mathematisches Modell, was ist überhaupt ein mathematisches Modell?
Gegeben sei uns ein Gegenstand, den wir formal beschreiben möchten. Es kann sich um
ein technisches System handeln, dessen Verhalten es zu beschreiben gilt; es kann sich
um einen Körper handeln, dessen Aufenthalt im Raum zu beschreiben ist; es kann sich
um eine bestimmte Art von Ereignis handeln, dessen Auftreten zeitlich zu erfassen ist.
In einem ersten Schritt hin zu einer Formalisierung des Sachverhaltes müssen wir die
Menge von Situationen spezifieren, die wir unter Bezugnahme auf ausgewählte Aspekte erfassen wollen. Dies kann dadurch erfolgen, daß wir gewisse Merkmale auswählen,
die manchmal erfüllt sind und manchmal nicht und die zusammengenommen zur Charakterisierung einer Situation ausreichen. Beim technischen System handle es sich beispielsweise um eine Waage und interessiere die Gesamtheit möglicher Meßergebnisse.
Ein Merkmal wäre, daß sich das Gewicht in einem gewissen Bereich befindet. Beim
beweglichen Körper interessiert der Raumpunkt, in dem er sich aufhält. Je einem mehr
oder weniger weit ausgedehnten Raumbereich ist ein Merkmal zuordenbar. Beim zeitlich auszuwertenden Ereignis könnte es sich etwa um radioaktiven Zerfall handeln;
von Interesse wären dann die Zeitpunkte der einzelnen Zerfallsvorgänge. Ein Merkmal
kann einem Zeitintervall entsprechen, daß innerhalb dessen ein Zerfall stattgefunden
hat.
Wir gehen also von einer gewissen Grundmenge zu unterscheidender Situationen aus;
man spricht häufig von einer sogenannten Mengen möglicher Welten. Dieser Menge
erfaßbarer Situationen sind des weiteren Merkmale zugeordnet, die in einer gegebenen
unter den Situationen gelten oder nicht; wir sprechen im weiteren von Eigenschaften.
Formal haben wir es mit einer abstrakten Menge zu tun, deren Elemente mögliche
Welten heißen, sowie mit einem System von Teilmengen dieser Menge, welche, wie es
heißt, je eine Eigenschaft modellieren oder repräsentieren. Im Fall des ersten obigen
Beispiels besteht die Menge möglicher Welten aus reellen Zahlen, die je ein Gewicht
repräsentieren; die Eigenschaft, sich in einem Gewichtsbereich aufzuhalten, wird durch
je ein Zahlenintervall modelliert.
Was bedeutet nun, den so erfaßten Gegenstand zu beschreiben“? Beschreiben bedeu”
tet, die hergenommenen Situationen in wechselseitige Zusammenhänge zu setzen. Es
gibt zwei Möglichkeiten. Zum einen können die wechselseitigen Beziehungen zwischen den möglichen Welten beschrieben werden. Auf den Elementen der reellen Zahlen gilt eine Ordnungsrelation und ist eine Addition definierbar. Dies bedeutet, die
Menge möglicher Welten mit einer Struktur auszustatten, was uns zur Prädikatenlogik
erster Stufe führt.
Dies ist jedoch nicht das uns bewegende Thema. Je eine mögliche Welt kann mit
der Gesamtheit der in ihr geltenden Eigenschaften identifiziert werden. Beispielsweise
kann je ein Gewicht mit dem – einelementigen – Durchschnitt all dieses enthaltender
Gewichtsbereiche identifiziert werden. Wir wollen im weiteren auf der Ebene der Ei5
genschaften bleiben, die zu den möglichen Welten überhaupt erst geführt haben. In
wechselseitige Beziehungen setzen wir im Rahmen dieser bescheideneren und grundlegenderen Herangehensweise die Eigenschaften selbst.
Es sei W unsere Menge möglicher Welten. Es mögen ϕ und ψ zwei Eigenschaften
symbolisieren. Die Menge A modelliere ϕ, die Menge B modelliere ψ. Die Beziehung,
die zwischen A und B herrschen kann, ist die mengentheoretische Inklusion: daß A in
B enthalten ist. Ist dies der Fall, gilt ψ stets, wenn ϕ gilt. Gemäß unserem Modell steht
ϕ für eine Eigenschaft, die stärker ist als ψ; wir sagen auch, daß ϕ ψ impliziert.
Wenn man des weiteren mit einer ganzen Reihe von Eigenschaften zu tun hat, kann
man im Rahmen des Modells aus diesen neue konstruieren. Wird wiederum ϕ durch
A und ψ durch B repräsentiert, kann ich die Mengen A ∩ B sowie A ∪ B bilden. Es
liegt nahe festzulegen, daß diese Mengen die Eigenschaften ϕ und ψ“ bzw. ϕ oder
”
”
ψ“ repräsentieren.
Wenn wir genau so weit und nicht weiter gehen – dann gelangen wir zum Begriff
des distributiven Verbandes, der in diesem ersten Kapitel unser Thema ist. Sehen wir
zunächst, wie eine Menge von Teilmengen hinsichtlich der Teilmengenbeziehung strukturiert werden kann.
Lemma 2.1.1. Es sei W eine nichtleere Menge. Weiter sei L eine Menge von Teilmengen von W . Dann gilt für alle A, B, C ∈ L:
(i) A ⊆ A.
(ii) Aus A ⊆ B und B ⊆ A folgt A = B.
(iii) Aus A ⊆ B und B ⊆ C folgt A ⊆ C.
Sehen wir sodann, welche Eigenschaften die beiden Mengenoperationen ∩ und ∪ haben.
Definition 2.1.2. Es sei W eine nichtleere Menge. Weiter bestehe L aus Teilmengen
von W dergestalt, daß mit A und B jeweils auch A ∩ B und A ∪ B in L ist. Dann heiße
(L; ∩, ∪) ein Teilmengenverband.
Insbesondere ist der Fall denkbar, daß L die Potenzmenge PW von W ist. PW , zusammen mit ∩ und ∪, ist ein Teilmengenverband..
Wir werden später beweisen, daß die im Folgenden aufgeführten Eigenschaften für
einen Teilmengenverband charakteristisch sind.
Lemma 2.1.3. Es sei (L; ∩, ∪) ein Teilmengenverband. Dann gilt für alle A, B, C ∈
L:
(i) A ∩ A = A ∪ A = A.
(ii) A ∩ B = B ∩ A und A ∪ B = B ∪ A.
(iii) A ∩ (B ∩ C) = (A ∩ B) ∩ C und A ∪ (B ∪ C) = (A ∪ B) ∪ C.
6
(iv) A ∩ (A ∪ B) = A ∪ (A ∩ B) = A.
(v) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) und A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
Es sind tatsächlich nur“ genau die in Lemma 2.1.3 aufgeführten Eigenschaften, um
”
die es im weiteren geht. Wenn in den Kapiteln 2 und 3 von Verbänden die Rede sein
wird, braucht man sich nichts als die vorstehende Struktur eines Teilmengenverbandes
vor Augen zu halten.
2.2 Posets
Wir beginnen den formalen Teil.
Wir abstrahieren vom vorstehenden Beispiel; wir tragen die Eigenschaften eines Systems von Teilmengen einer fixen Menge zusammen. Wir haben gesehen, daß wir einerseits von der ⊆-Beziehung und andererseits von den Operationen ∩ und ∪ ausgehen
können. Wir wenden uns zunächst der ersteren Möglichkeit zu.
Definition 2.2.1. Es sei (L; ≤) eine Algebra mit der zweistelligen Relation ≤. Dann
heiße L eine partiell geordnete Menge [engl. partially ordered set], oder kurz Poset,
falls für alle a, b, c ∈ L Folgendes gilt:
(P1) a ≤ a (Reflexitivität).
(P2) Aus a ≤ b und b ≤ a folgt a = b (Antisymmetrie).
(P3) Aus a ≤ b und b ≤ c folgt a ≤ c (Transitivität).
Je zwei Elemente a, b ∈ L, für die entweder a ≤ b oder b ≤ a gilt, heißen vergleichbar.
Sind je zwei Elemente vergleichbar, heißt (L; ≤) eine linear geordnete Menge [engl.
linearly oder totally ordered set].
Für Elemente eines Posets schreiben wir im weiteren a < b, falls a ≤ b, aber nicht
a = b gilt. Zudem schreiben wir gelegentlich b ≥ a für a ≤ b.
Lemma 2.2.2. Es sei L eine Menge von Teilmengen einer nichtleeren Menge. Dann ist
(L; ⊆) ein Poset.
Beweis. Siehe Lemma 2.1.1.
Beispiel 2.2.3. Wir geben zwei weitere immer wiederkehrende Beispiele von Posets
an.
(i) Es sei [0, 1] = {r ∈ R : 0 ≤ r ≤ 1} das reelle Einheitsintervall. Es gelte r ≤ s,
falls r kleiner oder gleich s gemäß der üblichen Ordnung reeller Zahlen ist. Dann
ist ([0, 1]; ≤) ein Poset. Es handelt sich um die natürliche Ordnung auf [0, 1].
Für je zwei Elemente r, s ∈ [0, 1] gilt entweder r ≤ s oder s ≤ r: [0, 1] ist sogar
eine linear geordnete Menge.
7
(ii) Es sei M eine nichtleere Menge. Eine Fuzzymenge über M ist eine Abbildung
von M nach [0, 1]. Es sei F (M ) die Menge aller Fuzzymengen über M . Wir
definieren für zwei Fuzzymengen u und v
u≤v
falls u(m) ≤ v(m) für alle m ∈ M .
Dies ist die punktweise Ordnung von F (M ). Dann ist (F (M ); ≤) ein Poset.
Visualisierung von Posets
Um sich über die Bedeutung von Resultaten über Posets ins klare zu setzen, kann man
jederzeit eines der Standardbeispiele verwenden, wozu insbesondere die Teilmengenposets gehören. Darüberhinaus ist es häufig nützlich, sich Fakten anhand endlicher
Posets klarzumachen oder auch an endlichen Teilstrukturen von Posets.
Zu diesem Zweck besteht eine einfache Möglichkeit der Visualisierung. Man stellt
jedes Element des endlichen Posets (L; ≤) durch einen Punkt dergestalt dar, daß, falls
für zwei Elemente a, b ∈ L a ≤ b gilt, b ∈ L höher zu liegen kommt als a ∈ L.
Sodann verbindet man a und b, falls a ≤ b gilt und es kein c mit a < c < b gibt. Das
Ergebnis nennt sich Hassediagramm.
Betrachtet sei beispielsweise die Menge {0, 1, 2, 3}, versehen mit der natürlichen Ordnung, des weiteren die Potenzmenge der zweielementigen Menge {0, 1}, versehen mit
der Mengeninklusion, und schließlich die Potenzmenge der zweielementigen Menge
{0, 1} ohne die Menge {0, 1}, ebenfalls versehen mit der Mengeninklusion.
({0, 1, 2, 3}, ≤)
(P{0, 1}, ⊆)
({∅, {0}, {1}}, ⊆)
Konstruktionen mit Posets
Von einem Poset kann man zu einer Teilmenge übergehen; dann läßt sich die partielle
Ordnung der größeren Menge problemlos auf die kleinere übertragen.
Lemma 2.2.4. Es sei (L; ≤) ein Poset und A ⊆ L. Für a, b ∈ A setzen wir a ≤ b, falls
dies in L gilt. Dann ist (A; ≤) wiederum ein Poset.
Beweis. Reflexitivität, Antisymmetrie und Transitivität gelten in A, da sie in P gelten.
Definition 2.2.5. Es sei (L; ≤) ein Poset und A ⊆ L. Für je zwei Elemente a, b ∈ A
erklären wir, daß a ≤ b gilt, wenn dies für a und b als Elemente von L der Fall ist.
Dann heiße (A; ≤) Unterposet von L.
8
Weiter setzen wir für Elemente p, q ∈ L mit p < q
[p, q] = {a ∈ L : p ≤ a ≤ q}.
Dann heißt der Unterposet von L mit dem Grundbereich [p, q] Intervall des Posets L.
Wir betrachten im weiteren jede Teilmenge eines Posets ohne expliziten Hinweis immer als Unterposet.
Beispiel 2.2.6. Zu beachten ist, daß ein Intervall eines Posets, auch wenn es die Bezeichnung nahelegen mag, keineswegs linear geordnet sein muß. Z.B. seien die folgenden Posets betrachtet:
L
[a, e]
Dann besteht das Intervall [a, e] von L aus allen Elementen von L außer d.
Weiter kann man in einem Poset die Ordnung umdrehen; es ergibt sich wiederum ein
Poset.
Lemma 2.2.7. Es sei (L; ≤) ein Poset. Für a, b ∈ A setzen wir a ≤′ b, falls b ≤ a gilt.
Dann ist (L; ≤′ ) wiederum ein Poset.
Beweis. Die Gültigkeit der Axiome (P1) bis (P3) bleibt erhalten, wenn man ≤“ überall
”
durch ≥“ ersetzt.
”
Definition 2.2.8. Es sei (L; ≤) ein Poset. Für a, b ∈ L erklären wir, daß a ≤′ b gilt,
falls b ≤ a. Dann heiße (L; ≤′ ) der zu (L; ≤) duale Poset.
Besondere Eigenschaften von Poset-Elementen
Wir stellen im weiteren besondere Eigenschaften von Elementen oder Elementpaaren
in Posets oder Unterposets zusammen.
Definition 2.2.9. Es sei (L; ≤) ein Poset, und es sei A eine (nicht notwendig nichtleere
und nicht notwendig echte) Teilmenge von L.
(i) Ein b ∈ L heiße untere Schranke [engl. lower bound] von A, falls b ≤ a für alle
a ∈ A.
Ein c ∈ L heiße obere Schranke [engl. upper bound] von A, falls a ≤ c für alle
a ∈ A.
9
(ii) Ein b ∈ A heiße kleinstes Element [engl. least element] von A, falls b ≤ a für
alle a ∈ A.
Ein c ∈ A heiße größtes Element [engl. greatest element] von A, falls a ≤ c für
alle a ∈ A.
(iii) Ein b ∈ A mit der Eigenschaft, daß a ∈ A und a ≤ b stets a = b impliziert, heißt
minimales Element [engl. minimal element] in A.
Ein c ∈ A mit der Eigenschaft, daß a ∈ A und c ≤ a stets a = c impliziert, heißt
maximales Element [engl. maximal element] in A.
Minimale und maximale Elemente dürfen nicht mit kleinsten bzw. größten Elementen
verwechselt werden. An letzteren gibt es nur je eines; erstere kann es viele geben.
Lemma 2.2.10. Es sei (L; ≤) und A ⊆ L. Dann gibt es höchstens ein kleinstes und
höchstens ein größtes Element von A.
Ein kleinstes Element von A ist minimales Element von A. Ein größtes Element von A
ist maximales Element von A.
Beweis. Es sei b1 ∈ L und b2 ∈ L jeweils kleinstes Element von A. Dann gilt b1 ≤ b2
und b2 ≤ b1 , also b1 = b2 . Also gibt es nicht mehr als ein kleinstes Element, und
ähnlich folgt, daß es nicht mehr als ein größtes Element gibt.
Es sei b das kleinste Element von A und a ≤ b für ein a ∈ A. Da dann auch b ≤ a
gilt, folgt a = b. Also ist b minimal. Ebenso folgt, das ein größtes Element maximal
ist.
Definition 2.2.11. Es sei (L; ≤) ein Poset und A ⊆ L. Existiert ein kleinstes Element
von A, wird dieses mit min A bezeichnet. Existiert ein größtes Element von A, wird
dieses mit max A bezeichnet.
Besitzt der gesamte Poset ein kleinstes oder/und ein größtes Element vorhanden, spielt
dieses i.a. ein herausgehobene Rolle. Diese Elemente erhalten standardmäßig die Bezeichnung 0 bzw. 1.
Definition 2.2.12. Es sei (L; ≤) ein Poset. Besitzt L ein kleinstes Element 0, heißt 0
das Nullelement. Besitzt L ein größtes Element 1, heißt 1 das Einselement.
Beispiel 2.2.13. Wir betrachten zwei endliche Posets sowie einige der Posets aus Beispiel 2.2.3.
(i) Gegeben seien folgende Posets.
M3
L
10
Im Poset M3 ist e kleinstes und a größtes Element. Weitere minimale und maximale Elemente von M3 gibt es nicht. Der Poset L besitzt das kleinste Element e,
jedoch kein größtes Element. Hingegen sind a und d maximale Elemente von L.
(ii) Das reelle Einheitsintervall [0, 1], versehen mit der natürlichen Ordnung, hat ein
Null- und ein Einselement – die ebenso bezeichneten reellen Zahlen.
(iii) Das offene reelle Intervall (0, 1), versehen mit der natürlichen Ordnung, hat weder ein Null- noch ein Einselement. Das gleiche gilt für R, die ganze reelle Zahlenachse.
(iv) Die Menge F (M ) der Fuzzymengen über einer Menge M , versehen mit der
punktweisen Ordnung, hat Null- wie Einselement, die wir mit 0̄ und 1̄ bezeichnen:
0̄ : M → [0, 1], m 7→ 0,
1̄ : M → [0, 1], m →
7 1.
Hat ein Poset kein Null- oder Einselement, läßt sich ein solches hinzufügen; folgende
Konstruktion ist möglich.
Satz 2.2.14. Es sei (L; ≤) ein Poset. L besitze kein Nullelement. Es sei 0 ein neues
˙
Element und L0 = L∪{0};
für a, b ∈ L0 gelte a ≤ b, falls entweder a, b ∈ L ist und
dies in L gilt oder wenn a = 0 ist. Dann ist L0 ein Poset.
Die entsprechende Konstruktion ist möglich, wenn L kein Einselement besitzt. Schließlich ist auch das gleichzeitige Hinzufügen von Null- und Einselement möglich.
Beweis. Es ist leicht nachzuprüfen, daß (L0 ; ≤) ein Poset ist.
Man beachte, daß im Fall, daß Satz 2.2.14 zum Zuge kommt, der Verband L notwendigerweise unendlich ist; ein endlicher Verband hat ohnehin immer ein Null- und Einselement.
Aufeinanderfolgende Elemente von Posets
Das reellle Einheitsintervall [0, 1], versehen mit der natürlichen Ordnung, ist das Beispiel eines Posets mit der folgenden Eigenschaft: Für jedes Paar von Elementen a, b
mit a < b gibt es ein drittes Element c mit a < c < b; man spricht daher von einer
dichten partiellen Ordnung. Im Gegensatz dazu betrachte man den Poset {0, n1 , . . . , 1}
für ein n ≥ 2, ebenfalls versehen mit der natürlichen Ordnung. Hier treten Paare a, b
von Elementen auf, so daß a < b gilt und es kein c mit a < c < b gibt. In einem naheliegenden Sinne hat hier jedes von 0 und 1 verschiedene Element einen unmittelbaren
Vorgänger und Nachfolger. Mit Posets solcher Art stellen wir einige Begrifflichkeiten
zusammen.
11
Definition 2.2.15. Es sei (L; ≤) ein Poset. Dann heißt a ∈ L unmittelbarer Vorgänger
von b ∈ L und b unmittelbarer Nachfolger von a, in Zeichen
a <· b,
falls a < b gilt und es kein c ∈ L mit a < c < b gibt.
In endlichen Posets hat jedes Element, das nicht minimal ist, einen unmittelbaren
Vorgänger. In der Tat genügt es im Fall eines endlichen Posets, alle Relationen der
Form a <· b zu spezifizieren; alle anderen ≤-Beziehungen folgen aus der Transitivität.
Dies ist in der Tat die Grundlage der oben erklärten Hassediagramme.
Die Nachbarn des Null- und Einselementes eines Posets erhalten spezielle Bezeichnungen.
Definition 2.2.16. Es sei (L; ≤) ein Poset mit 0 und 1. Dann heißt ein Element a mit
0 <· a ein Atom von L. Die Menge aller Atome von L bezeichnen wir mit A(L).
Ein Element a mit a <· 1 heiße Koatom von L.
Beispiel 2.2.17. Wir rekapitulieren des weiteren einen Teil von Beispiel 2.2.3.
(iv) Die Beispiele von 0, 1-Verbänden aus (i) und (iii) besitzen keine Atome und
keine Koatome. Für den ersten Fall sei dies begründet: Angenommen, a ∈ [0, 1]
sei ein Atom von [0, 1]; dann wäre 0 <· a; dies ist wegen 0 < a2 < a jedoch
nicht der Fall.
Wir betrachten eine Modifierung von Beispiel (iii). Es sei für M 6= ∅ und n ≥ 1
Ln = {0, n1 , n2 , . . . , 1} und
Fn (M ) = {u : M → Ln },
versehen mit der punktweisen Ordnung. Dann ist jedes u ∈ Fn (M ), welches für
ein l ∈ M alle m ∈ M \{l} auf 0 abbildet und l auf n1 , ein Atom. Entsprechend
ist jedes u ∈ Fn (M ), welches für ein l ∈ M alle m ∈ M \{l} auf 1 abbildet
und l auf 1 − n1 , ein Koatom.
Schließlich definieren wir, anschaulich mit Bezug auf Hassediagramm gesprochen, die
Ausdehung eines Posets in vertikaler Richtung.
Definition 2.2.18. Es sei (L; ≤) ein Poset mit 0 und 1, und a ∈ L. Es gebe ein natürliches n ≥ 1 mit folgender Eigenschaft: Die Kardinalität des größten linear geordneten
Unterposets von [0, a] sei n. Dann heiße n − 1 die Höhe [engl. height] von a und werde
durch h(a) bezeichnet. Wir sagen in diesem Fall zudem, daß a von endlicher Höhe ist.
Ist weiter 1 von endlicher Höhe, heiße h(1), die Höhe von 1, die Länge [engl. length]
von L. Wir sagen in diesem Fall zudem, daß L von endlicher Länge ist.
Besitzt also ein Poset L die Länge n, gibt es Elemente von L mit
0 = a0 <· a1 <· . . . <· an−1 <· an = 1,
und es gibt keine solche Kette von Elementen, die länger wäre.
12
Beispiel 2.2.19.
Länge 2.
(i) Die Posets M3 und L aus Beispiel 2.2.13 haben jeweils die
(ii) Das reelle Einheitsintervall [0, 1], versehen mit der natürlichen Ordnung, ist von
unendlicher Länge.
Homomorphismen von Posets
Vielfach werden wir es zu tun haben mit Funktionen, die einen Poset auf einen anderen
abbilden. Dabei interessiert der Fall, daß die Ordnungsrelation erhalten bleibt.
Definition 2.2.20. Es seien (P ; ≤) und (Q; ≤) zwei Posets. Eine Abbildung ϕ : P →
Q heiße Ordnungshomomorphismus oder ordnungserhaltend oder monoton, falls für
alle a, b ∈ P gilt:
Aus a ≤ b folgt ϕ(a) ≤ ϕ(b).
ϕ : P → Q heiße Ordnungsisomorphismus, falls ϕ bijektiv ist und für alle a, b ∈ P
Folgendes gilt:
a ≤ b genau dann, wenn ϕ(a) ≤ ϕ(b).
Ebenfalls von regelmäßigem Interesse ist der Fall, daß sich die Ordnungsrelation unter
einer Abbildung umdreht.
Definition 2.2.21. Es seien (P ; ≤) und (Q; ≤) zwei Posets. Ein Ordnungshomomorphismus von P auf den zu Q dualen Poset heißt Ordnungsantihomomorphismus oder
antiton.
Ein Ordnungsisomorphismus zwischen P und dem zu Q dualen Poset heißt Ordnungsantiisomorphismus.
Mit anderen Worten ist eine antitone Abbildung zwischen Posets P und Q dergestalt,
daß für alle a, b ∈ P gilt:
Aus a ≤ b folgt ϕ(b) ≤ ϕ(a).
Und um einen Ordnungsantiisomorphismus zu charakterisieren, ist hierin die Implikation durch eine Äquivalenz zu ersetzen.
2.3 Verbände
Die im weiteren zentrale Definition ist die folgende.
Definition 2.3.1. Es sei (L; ≤) ein Poset, und es sei A eine Teilmenge von L. Dann
heiße b ∈ L Infimum [engl. infimum] von A, falls b größtes Element der Menge der
unteren Schranken von A ist. Existiert dieses Element, bezeichnen wir es durch
^
A
13
oder alternativ
a1 ∧ . . . ∧ an ,
falls A = {ai : i = 1, . . . , n}, n ≥ 2.
Ebenso heiße c ∈ L Supremum [engl. supremum] von A, falls c kleinstes Element der
Menge der oberen Schranken von A ist. Existiert dieses Element, bezeichnen wir es
durch
_
A
oder alternativ
a1 ∨ . . . ∨ an ,
falls A = {ai : i = 1, . . . , n}, n ≥ 2.
Gemäß Lemma 2.2.10 hat jede Menge höchstens ein größtes und ein kleinstes Element;
nur deshalb ist die vorstehende Definition
sinnvoll. Man beachte, daß, wenn A TeilmenV
ge eines Posets ist, der Ausdruck A für sich genommen nicht notwendig einen Sinn
ergibt;
das Infimum einer Teilmenge kann existieren, muß aber nicht. Dasselbe gilt für
W
A, das Supremum.
Infimum und Supremum interessieren am häufigsten für Paare a1 , a2 eines Posets. Man
mache sich für diesen Fall die Definition klar. Ist b deren Infimum, ist b größte untere
Schranke von a1 und a2 . Das heißt zweierlei:
(1) b ≤ a1 , a2 ;
(2) wenn b′ ≤ a1 , a2 für ein weiteres Element gilt, folgt b′ ≤ b.
Analoges gilt fürs Supremum; ist c Supremum von a1 und a2 , ist c kleinste obere
Schranke von a1 und a2 :
(1) a1 , a2 ≤ c;
(2) wenn a1 , a2 ≤ c′ für ein weiteres Element gilt, folgt c ≥ c′ .
Beispiel 2.3.2. Wir betrachten Beispiel 2.2.3 sowie gewisse Modifikationen.
(i) Sind Elemente a und b eines Posets vergleichbar, besitzen sie stets Infimum und
Supremum. Gilt etwa a ≤ b, ist a ∧ b = a und a ∨ b = b.
Insbesondere besitzen in der linear geordneten Menge ([0, 1]; ≤) je zwei Elemente ein Infimum und ein Supremum.
(ii) Es sei (F (M ); ≤) die Menge der Fuzzymengen über M , versehen mit der punktweisen Ordnung. Es seien u, v : M → [0, 1] Fuzzymengen über M . Die Zielmenge [0, 1] ist standardmäßig mit der natürlichen Ordnung ausgestattet; für
r, s ∈ [0, 1] schreiben wir r ∧ s für das kleinere und r ∨ s für das größere
Element.
14
Wir setzen
s : M → [0, 1], m 7→ u(m) ∧ v(m),
t : M → [0, 1], m →
7 u(m) ∨ v(m).
Wir behaupten, daß s das Infimum und t das Supremum von u und v ist. Wir
zeigen ersteres.
(1) Für jedes m gilt s(m) = u(m) ∧ v(m) ≤ u(m), also s ≤ u. Ebenso folgt
s ≤ v.
(2) Die Fuzzymenge s′ sei dergestalt, daß s′ ≤ u, v. Dann ist für jedes m ∈ M
s′ (m) ≤ u(m), v(m). Für das Infimum u(m) ∧ v(m), als die größte untere
Schranke von u(m) und v(m), folgt s′ (m) ≤ u(m) ∧ v(m) = s(m). Also
s′ ≤ s.
Wir haben gezeigt, daß s größte untere Schranke von u und v ist, d.h. s = u ∧ v.
(iii) Es sei (C 1 (R); ≤) die Menge aller stetig differenzierbaren Funktionen, versehen
mit der punktweisen Ordnung. Für zwei Funktionen f, g ∈ C 1 (R) existiert im
allgemeinen weder Infimum noch Supremum.
Um dies zu sehen, betrachte man die Funktionen f und g, definiert durch f (x) =
x und g(x) = −x. Es sei h ∈ C 1 (R) eine untere Schranke von f und g. Dann ist
h(0) < 0; denn im Fall h(0) = 0 wäre h am Punkt 0 nicht differenzierbar. Dann
aber läßt sich zeigen, daß es eine Funktion h′ ∈ C 1 (R) mit h < h′ ≤ f, g gibt.
Es folgt, daß es keine größte untere Schranke von f und g gibt, d.h. f und g kein
Infimum besitzen.
Wir kommen zur zentralen Definition.
Definition 2.3.3. Es sei (L; ≤) ein Poset, so daß Infimum und Supremum je zweier
Elemente existieren. Dann heiße L verbandsgeordnet.
Wir fassen in diesem Fall ∧ und ∨ als zwei binäre Operationen auf L auf. Die so
entstandene Algebra (L; ∧, ∨) heiße Verband.
M.a.W. ist ein Verband eine Algebra (L; ∧, ∨) mit zwei binären Operationen ∧ und
∨, welche mittels Definition 2.3.1 aus einer partiellen Ordnung auf L hervorgegangen
sind. Sinnvoll ist der zweite Teil von Definition 2.3.3 deshalb, weil sich die partielle
Ordnung, von der man ausgegangen ist, aus ∧ oder ∨ eindeutig wieder zurückgewinnen
läßt.
Lemma 2.3.4. Es sei (L; ≤) ein Poset, und L sei verbandsgeordnet. Dann gilt für alle
a, b ∈ L
a ≤ b, gdw a ∧ b = a, gdw a ∨ b = b.
(1)
Insbesondere gilt: Ist (L; ∧, ∨) ein Verband, gibt es genau eine partielle Ordnung auf
L, bezüglich deren ∧ und ∨ je zwei Elementen deren Infimum und Supremum zuordnen.
15
Beweis. Aus a ≤ b folgt offenbar a ∧ b = a. Umgekehrt heißt a ∧ b = a, daß
a = a ∧ b ≤ b.
Damit ist die erste Äquivalenz gezeigt. Die Äquivalenz von a ≤ b und a ∨ b = b folgt
analog.
Auf ≤ als diejenige Relation, aus der der Verband (L; ∧, ∨) hervorgeht, nehmen wir
als die unterliegende partielle Ordnung Bezug.
Lemma 2.3.5. Ein Teilmengenverband (L; ∩, ∪) ist ein Verband. Die unterliegende
partielle Ordnung ist die Teilmengenbeziehung ⊆.
Beweis. Gemäß Lemma 2.2.2 ist (L; ⊆) ein Poset. Nach Lemma 2.3.4 ist die partielle
Ordnung, die einem Verband unterliegt, eindeutig bestimmt. Wir behaupten, daß es
sich im vorliegenden Fall um ⊆ handelt.
Für A, B ∈ L sind gemäß Voraussetzung A ∩ B wie A ∪ B in L. A ∩ B ist die größte in
A und B enthaltende Menge; m.a.W. ist A ∩ B das Infimum von A und B bezüglich ⊆.
Ähnlich ist A ∪ B deren Supremum. Also ist (L; ∩, ∪) ein Verband mit unterliegender
Ordnung ⊆.
Die nächste Frage ist, wie sich ein Verband ohne Rückgriff auf die unterliegende partielle Ordnung charakterisieren läßt.
Satz 2.3.6. Es sei (L; ∧, ∨) ein Verband. Dann gilt für alle a, b, c ∈ L Folgendes:
(V1) a ∧ a = a ∨ a = a.
(V2) a ∧ b = b ∧ a und a ∨ b = b ∨ a.
(V3) a ∧ (b ∧ c) = (a ∧ b) ∧ c und a ∨ (b ∨ c) = (a ∨ b) ∨ c.
(V4) a ∧ (a ∨ b) = a ∨ (a ∧ b) = a.
Umgekehrt sei (L; ∧, ∨) eine Algebra mit den zweistelligen Operationen ∧ und ∨, so
daß für alle a, b, c ∈ L die Bedingungen (V1) bis (V4) erfüllt sind. Dann ist L ein
Verband, dessen unterliegende partielle Ordnung durch (1) gegeben ist.
Beweis. Zum Beweis des ersten Teils nehmen wir an, daß (L; ∧, ∨) ein Verband ist.
Für a, b ∈ L sind dann a ∧ b und a ∨ b Infimum und Supremum von a und b bezüglich
der partiellen Ordnung, die durch (1) bestimmt ist. Wir zeigen jeweils die erste Hälfte
der Behauptungen in (V1), ..., (V4); die zweite folgt jeweils analog.
(V1): a ∧ a ist das Infimum der einelementigen Menge {a}; dieses ist offenbar gleich
a.
(V2): Sowohl a ∧ b also auch b ∧ a bezeichnen das Infimum der Menge {a, b}.
(V3): Wir zeigen, daß a ∧ (b ∧ c) das Infimum der Menge {a, b, c} ist, womit die
Behauptung folgt. Für jedes x ∈ L folgt aus x ≤ a und x ≤ b ∧ c, daß x ≤ a, b, c
16
gilt; und umgekehrt folgt aus x ≤ a, b, c, daß x ≤ a, b ∧ c gilt. Also ist die Menge der
unteren Schranken von {a, b∧c} gleich der Menge der unteren Schranken von {a, b, c}.
Also ist auch das größte Element der unteren Schranken in beiden Fällen dasselbe, d.h.
a ∧ (b ∧ c) = a ∧ b ∧ c.
(V4): Aus a ≤ a ∨ b folgt a ∧ (a ∨ b) = a.
Um den zweiten Teil des Satzes zu beweisen, nehmen wir nunmehr an, daß (L; ∧, ∨)
eine Algebra ist, die (V1) bis (V4) erfüllt. Für a, b ∈ L setzen wir a ≤ b, falls a = a∧b.
Wir haben zu zeigen, daß (L; ≤) ein Poset ist. a ≤ a folgt aus (V1). Gilt a ≤ b und
b ≤ a, so a = a ∧ b und b = b ∧ a, und a = b folgt aus (V2). Schließlich sei a ≤ b und
b ≤ c. Dann gilt a = a ∧ b und b = b ∧ c, also a = a ∧ (b ∧ c) = (a ∧ b) ∧ c = a ∧ c
gemäß (V3).
Als nächstes zeigen wir (1); dafür ist nachzuweisen, daß a ≤ b, gdw a ∨ b = b. Aus
a ≤ b folgt a ∨ b = (a ∧ b) ∨ b = b ∨ (b ∧ a) = b gemäß (V4) und dem zweimal
angewendeten (V2). Umgekehrt folgt aus a ∨ b = b, daß a ∧ b = a ∧ (a ∨ b) = a,
wiederum gemäß (V4).
Weiter ist zu zeigen, daß für a, b ∈ L a∧b das Infimum bezüglich ≤ ist. Da (a∧b)∧a =
a ∧ (a ∧ b) = (a ∧ a) ∧ b = a ∧ b gemäß (V2), (V3) bzw. (V1) gilt, ist a ∧ b ≤ a. Da
auch (a ∧ b) ∧ b = a ∧ (b ∧ b) = a ∧ b gilt, ist a ∧ b ≤ b. Weiter sei x ≤ a, b. Dann ist
x ∧ (a ∧ b) = (x ∧ a) ∧ b = x ∧ b = x, also x ≤ a ∧ b. Die Behauptung folgt.
Als letztes ist zu zeigen, daß für a, b ∈ L a ∨ b das Supremum bezüglich ≤ ist. Es gilt
a ∧ (a ∨ b) = a gemäß (V4), also a ≤ a ∨ b. Ebenso gilt b ∧ (a ∨ b) = b ∧ (b ∨ a) = b
gemäß (V2) und (V4), also b ≤ a ∨ b. Weiter sei a, b ≤ x. Wir hatten (1) gezeigt; es
folgt (a ∨ b) ∨ x = a ∨ (b ∨ x) = a ∨ x = x und damit a ∨ b ≤ x. Die Behauptung
folgt.
Satz 2.3.6 besagt, daß sich Verbände auch mittels der Axiome (V1) bis (V4) definieren
ließen. Dies wäre technisch sogar einfacher, hieße allerdings das Pferd von hinten her
aufzuzäumen. Verbände wollen wir als partiell geordnete Mengen betrachten mit der
Zusatzeigenschaft, daß Infima und Suprema je zweier Elemente existieren. Daraus und
von nirgendwo andersher ergeben sich die Eigenschaften (V1) bis (V4).
Anmerkung 2.3.7. Unter den Verbände charakterisierenden Eigenschaften (V1) bis
(V4) ist (V1) redundant. In der Algebra (L; ∧, ∨) gelte (V4). Dann gilt a ∧ a = a ∧
(a ∨ (a ∧ a)) = a. Ähnlich folgt a ∨ a = a.
Man könnte meinen, daß in Anwendungen auftretende Posets typischerweise Verbände
sind. Dieser Eindruck ist auch mit dem Umstand konsistent, daß in dieser Vorlesung
Verbände und nicht Posets im Mittelpunkt stehen. Auch wenn dem in Wahrheit nicht
so sein mag – Beispiele von Posets, die keine Verbände sind, wirken häufig künstlich.
Beispiel 2.3.8. Wir rekapitulieren Beispiel 2.3.2 und ergänzen dieses.
(i) Jede linear geordnete Menge ist ein Verband.
(ii) Die Menge F (M ) der Fuzzymengen über einer Menge M , versehen mit der
punktweisen Ordnung, ist ein Verband.
17
(iii) Die Menge (C 1 (R); ≤) aller stetig differenzierbaren Funktionen auf R, versehen
mit der punktweisen Ordnung, ist kein Verband.
(iv) Wir betrachten verschiedene partielle Ordnungen auf dem Rn , n ≥ 1.
(α) Wir setzen (a1 , . . . , an ) ≤ (b1 , . . . , bn ), falls
a1 ≤ b 1 , . . . , an ≤ b n .
Dies ist die komponentenweise natürliche Ordnung auf dem Rn und macht
diesen zu einem Verband. Es handelt sich um einen Spezialfall von (ii).
(β) Wir setzen (a1 , . . . , an ) ≤lex (b1 , . . . , bn ), falls
a1 < b 1
oder
a1 = b1 und a2 < b2 oder
a1 = b1 , a2 = b2 und a3 < b3
oder
...
a1 = b1 , . . . , an−1 = bn−1 und an < bn
oder
a1 = b 1 , . . . , an = b n .
≤lex ist die lexikographische Ordnung auf dem Rn . Man überprüfe, daß
≤lex den Rn zu einer linear geordneten Menge macht, insbesondere also zu
einem Verband.
(γ) Fürs dritte Teilbeispiel setzen wir der Einfachheit halber n = 2. Wir setzen
(a1 , a2 ) 4 (b1 , b2 ), falls
(a1 , a2 ) = (b1 , b2 )
oder
a1 < b1 , und b1 < b2 .
Dies ist die sogenannte strikte Ordnung auf dem R2 . Man überzeuge sich,
daß 4 überhaupt eine partielle Ordnung ist.
Wir behaupten weiter, daß (R2 ; 4) kein Verband ist. In der Tat besitzt beispielsweise das Paar (0, 1) und (1, 0) kein Supremum. Die Menge der oberen Schranken ist nämlich
{(r, s) ∈ R2 : r > 1, s > 1};
diese Menge hat in bezug auf 4 kein kleinstes Element.
Wir haben Verbände als Algebren eingeführt, die je zwei (nicht notwendig verschiedenen) Elementen bezüglich einer partiellen Ordnung das Infimum und Supremum zuordnen. Wie das folgende Lemma zeigt, reichen die zweistelligen Operationen aus,
dasselbe für jede endliche Menge von Elementen zu tun.
Lemma 2.3.9. Es sei (L; ∧, ∨) ein Verband, und es seien a1 , . . . , an ∈ L, n ≥ 1.
Dann ist
(...(a1 ∧ a2 ) ∧ a3 ) ∧ . . . ∧ an−1 ) ∧ an
(2)
18
das Infimum der Menge {a1 , . . . , an }. Weiter können in (2) die Klammern nach Belieben versetzt werden und die Reihenfolge der Elemene nach Belieben verändert werden,
ohne daß sich der Wert verändern würde. Analoges gilt für das Supremum.
Beweis. Im Beweis von (V3), s. Satz 2.3.6, hatten wir gezeigt, daß für a, b, c ∈ L das
Infimum von a ∧ b und c gleich dem Infimum von a, b und c ist. Ähnlich können wir
ersehen, daß für a, b, c1 , . . . , ck ∈ L, worin k ≥ 1 ist, das Infimum von a∧b, c1 , . . . , ck
gleich dem Infimum von a, b, c1 , . . . , ck ist.
Mittels wiederholter Anwendung dieser Tatsache erschließen wir, daß (2) das Infimum
von a1 , . . . , an ist. Dabei kommt es offensichtlich weder darauf an, wie geklammert
ist, noch, in welcher Reihenfolge die ai stehen.
Hinsichtlich des Supremums gelten die analogen Überlegungen.
Lemma 2.3.9 impliziert zweierlei. Erstens lassen sich beliebige endliche Infima und
Suprema durch die zweistelligen Verbandsoperationen ∧ bzw. ∨ ausdrücken. Es seien
nämlich a1 , . . . , an Elemente des Verbandes (L; ∧, ∨); dann ist (2) deren Infimum.
Zweitens ist klar, daß die Klammerung nicht unbedingt gerade so wie in (2) erfolgen
muß; geklammert werden kann nach Belieben.
So sind die Klammern in (2) eigentlich überflüssig, und wir werden sie im Folgenden
grundsätzlich weglassen. Wir verwenden stattdessen den übersichtlicheren Ausdruck
a1 ∧ . . . ∧ an
und legen fest, daß dieser stellvertretend für (2) steht. Wenn wir L als einen Poset
betrachten, ist a1 ∧ . . . ∧ an ohnehin bereits als das Infimum von {a1 , . . . , an } definiert
und damit als dasselbe Element wie (2).
Posets, die die Bildung beliebiger Infima und Suprema erlauben, werden nunmehr
erwähnt.
Definition 2.3.10. Es sei (L; ∧, ∨) ein Verband. Für jede beliebige Teilmenge A von
L existiere das Infimum und das Supremum von A. Dann heiße L ein vollständiger
Verband.
Man braucht in diesem Fall nicht zu fordern, daß sowohl Infima als auch Suprema
existieren; es reicht, wenn z.B. alle Infima existieren.
Lemma 2.3.11. Es sei (L; ∧, ∨) ein Verband. Für jede beliebige Teilmenge A von L
existiere das Infimum von A. Dann ist L ein vollständiger Verband.
Beweis. Es sei A ⊆ L. Wir müssen zeigen, daß das Supremum von A existiert. Wir
setzen
^
c =
{b ∈ L : b ≥ a für alle a ∈ A};
dies ist das nach Voraussetzung existierende Infimum aller oberen Schranken von A.
Insbesondere ist c selbst obere Schranke und damit die kleinste obere Schranke.
19
Wir ergänzen ein paar im Folgenden immer wieder stillschweigend verwendeten Eigenschaften von Verbänden.
Lemma 2.3.12. Es sei (L; ∧, ∨) ein Verband. Dann gilt für alle a, b, c ∈ L:
(i) Aus a ≤ b und a ≤ c folgt a ≤ b ∧ c.
Aus b ≤ a und c ≤ a folgt b ∨ c ≤ a.
(ii) Aus b ≤ c folgt a ∧ b ≤ a ∧ c sowie a ∨ b ≤ a ∨ c.
Beweis. (i) a ≤ b, c bedeutet, daß a untere Schranke von b und c ist. Da deren Infimum
die größte untere Schranke ist, folgt a ≤ b ∧ c. Ähnlich ist für den zweiten Teil zu
argumentieren.
(ii) Es sei b ≤ c. Dann ist jede untere Schranke von a und b auch eine solche von a und
c. Also ist auch a ∧ b, die größte untere Schranke von a und b, eine untere Schranke
von a und c. Nach Teil (i) folgt a ∧ b ≤ a ∧ c.
Visualisierung von Verbänden
Um an endlichen Posets bestimmte Eigenschaften zu prüfen, bietet sich stets die Möglichkeit an, eine entsprechende Eigenschaft des zugehörigen Hassediagramms auszumachen. Es gibt kein sonderlich elegantes Verfahren, um festzustellen, ob ein Hassediagramm einen Verband repräsentiert – wir erwähnen dennoch ein solches.
Lemma 2.3.13. Es sei (L; ≤) ein endlicher Poset. Dann ist L ein Verband genau dann,
wenn es kein Paar a, b ∈ L verschiedener Elemente gibt, die eine der folgenden Bedingungen erfüllen:
(i) a und b besitzen keine untere oder keine obere Schranke.
(ii) Es gibt vier Elemente a, b, c, d mit a, b ≤ c, d, so daß es kein e ∈ L mit a, b ≤
e ≤ c, d gibt.
Beweis. Es sei L ein Verband. Für a, b ∈ L gibt es dann eine kleinste obere Schranke
a ∧ b und eine größte untere Schranke a ∨ b. Dies widerspricht sowohl (i) als auch (ii).
Es sei L kein Verband. Dann gibt es ein Paar a, b ∈ L, so daß die Menge U der unteren
Schranken von a und b kein größtes Element hat oder die Menge O der oberen Schranken kein kleinstes. Wir nehmen den letzteren Fall an; für den ersteren argumentieren
wir analog. Notwendigerweise muß a 6= b gelten. Ist O leer, gilt (i). O sei nichtleer.
Da O endlich ist, gibt es für jedes x ∈ O ein minimales Element y in U mit y ≤ x.
Also enthält O mindestens ein minimales Element. Enthielte O genau ein minimales
Element, wäre dies das kleinste Element von O, entgegen der Annahme. Also gibt es
zwei verschiedene minimale Elemente c und d in U , und es folgt (ii).
Insofern ist ersichtlich, daß folgendes Beispiel L1 ein Verband ist, L2 mangels Existenz
einer oberen Schranke von a und b kein Verband ist und L3 , da d, e ≤ b, c gilt, es jedoch
kein Element x gibt mit d, e ≤ x ≤ b, c, ebenfalls kein Verband ist.
20
L1
L2
L3
Konstruktionen mit Verbänden
Wir betrachten als nächstes die Möglichkeit, den Grundbereich eines Verbandes zu
verkleinern. Im Fall eines Posets stellt dies kein Problem dar; im Fall eines Verbandes
ist etwas Vorsicht geboten.
Definition 2.3.14. Es sei (L; ∧, ∨) ein Verband. Weiter sei A ⊆ L, und mit a, b ∈ A
sei auch a ∧ b ∈ A und a ∨ b ∈ A. Wir erklären die Operationen ∧ und ∨ durch
Einschränkung dieser Operationen von L auf A. Dann heißt (A; ∧, ∨) Unterverband
von L.
Lemma 2.3.15. Der Unterverband (A; ∧, ∨) eines Verbandes (L; ∧, ∨) ist ebenfalls
ein Verband.
Beweis. Die Gleichungen (V1) bis (V4) gelten in L, also auch in A.
Allerdings ist Folgendes zu beachten. Ist L ein Verband und A ⊆ L, ist A stets ein Unterposet. Dieser Unterposet ist im allgemeinen kein Unterverband: A ist unter den auf
L erklärten Operationen ∧ und ∨ nicht notwendig abgeschlossen. Wenn A kein Unterverband von L ist, kann A nichtsdestoweniger verbandsgeordnet sein. Dieser Fall tritt
auf, wenn A unter den auf L erklärten Operationen ∧ und ∨ zwar nicht abgeschlossen
ist, in A aber alle Infima und Suprema von Paaren existieren.
Man betrachte das folgende Beispiel:
L′
L
Der aus der Teilmenge L′ = {a, b, c, g} gebildete Unterposet von L ist ein Verband,
aber kein Unterverband von (L; ∧, ∨). Das Infimum von b und c ist e in L, in L′ aber
g.
Weiter können wir von einem Verband, als Poset gesehen, zum dualen Poset übergehen;
das Ergebnis ist wieder ein Verband.
21
Lemma 2.3.16. Es sei (L; ∧, ∨) ein Verband. Es sei ≤ die unterliegende Ordnung und
≤′ die zugehörige duale Ordnung. Dann ist (L; ≤′ ) wiederum verbandsgeordnet. Es
seien ∧′ und ∨′ die zugehörigen Verbandsoperationen; dann ist ∧′ = ∨ und ∨′ = ∧.
Beweis. Ein Element c ∈ L ist bezüglich ≤′ das Infimum von a und b, wenn c ≤′ a, b
gilt und aus x ≤′ a, b stets c ≤′ x folgt; wenn also a, b ≤ c gilt und aus a, b ≤ x stets
x ≤ c folgt; wenn also c das Supremum von a und b bezüglich ≤ ist.
Also ist a ∨ b das Infimum von a und b bezüglich ≤′ , und ebenso ist zu ersehen, daß
a ∧ b das Suprumum von a und b bezüglich ≤′ ist.
Definition 2.3.17. Es sei (L; ∧, ∨) ein Verband. Dann heiße (L; ∧′ , ∨′ ) der zu L duale
Verband, worin ∧′ = ∨ und ∨′ = ∧.
Der Übergang von einem Verband zum dualen Verband bedeutet also, daß ∧ und ∨
vertauscht werden. Daß sich dadurch wiederum ein Verband ergibt, ist im übrigen an
den Bedingungen (V1) bis (V4) zu ersehen; diese sind in ∧ und ∨ symmetrisch.
Wir schließen mit einer in der Algebra häufig angewandten Konstruktion.
Definition 2.3.18. Es seien (Lι ; ∧ι , ∨ι ), ι ∈ I, Verbände. Wir setzen
Y
L =
Lι
ι∈I
und definieren für (aι )ι , (bι )ι ∈ L
(aι )ι ∧ (bι )ι = (aι ∧ι bι )ι ,
(aι )ι ∨ (bι )ι = (aι ∨ι bι )ι .
Dann heißt (L; ∧, ∨) das direkte Produkt [engl. direct product] der Verbände Lι .
Lemma 2.3.19. Das direkte Produkt von Verbänden ist wiederum ein Verband.
Beweis. Jede Gleichung, die in jedem der Verbände gilt, gilt auch im Produkt. Also
gelten die Verbandsaxiome.
Definition 2.3.20. Wir sagen, daß ein Verband L unzerlegbar ist, falls L nicht dem
direkten Produkt mindestens zweielementiger Verbände L1 und L2 isomorph ist.
Homomorphismen von Verbänden
Wir definieren strukturerhaltende Abbildungen zwischen Verbänden.
Definition 2.3.21. Es seien (P ; ∧, ∨) und (Q; ∧, ∨) zwei Verbände. Eine Abbildung
ϕ : P → Q heiße Verbandshomomorphismus, falls für alle a, b ∈ P gilt:
ϕ(a ∧ b) = ϕ(a) ∧ ϕ(b),
ϕ(a ∨ b) = ϕ(a) ∨ ϕ(b).
22
Ist ϕ : P → Q injektiv, heißt ϕ auch eine Einbettung, und wir sagen, daß sich P in Q
einbetten läßt.
Ist ϕ : P → Q surjektiv, sagen wir, daß Q ein homomorphes Bild von P ist.
Ist ϕ : P → Q bijektiv, heißt ϕ ein Verbandsisomorphismus.
Da jeder Verband auch ein Poset ist, ist das Verhältnis zwischen Verbands- und Posethomomorphismus zu klären.
Lemma 2.3.22. Es seien (P ; ∧, ∨) und (Q; ∧, ∨) Verbände.
(i) ϕ : P → Q sei ein Verbandshomomorphismus. Dann ist ϕ ordnungserhaltend.
(ii) ϕ : P → Q sei ein Ordnungsisomorphismus. Dann ist ϕ ein Verbandsisomorphismus.
Beweis. (i) Ist a ≤ b, so a = a ∧ b, also ϕ(a) = ϕ(a ∧ b) = ϕ(a) ∧ ϕ(b) ≤ ϕ(b).
(ii) Wir zeigen, daß ϕ(a ∧ b) das Infimum von ϕ(a) und ϕ(b) ist. Da a ∧ b ≤ a, b,
gilt ϕ(a ∧ b) ≤ ϕ(a), ϕ(b). Es sei x ≤ ϕ(a), ϕ(b). Wegen der Bijektivität von ϕ ist
x = ϕ(c) für ein c ∈ P ; und weil ϕ ein Ordnungsisomorphismus ist, folgt aus ϕ(c) ≤
ϕ(a), ϕ(b), daß c ≤ a und c ≤ b gilt. Also c ≤ a ∧ b und weiter x = ϕ(c) ≤ ϕ(a ∧ b).
Also ϕ(a ∧ b) = ϕ(a) ∧ ϕ(b), und ähnlich erschließen wir ϕ(a ∨ b) = ϕ(a) ∨ ϕ(b).
Hingegen ist zu beachten, daß eine ordnungserhaltende Abbildung zwischen Verbänden
nicht notwendig ein Verbandshomomorphismus ist.
2.4 Distributive Verbände
Wir kommen zu einer weiteren Eigenschaft, die Verbände erfüllen können. Wie wir gezeigt haben, sind für Verbände die Eigenschaften (i) bis (iv) eines Teilmengenverbandes
maßgeblich, s. Lemma 2.1.3. Die Eigenschaft (v) ist bislang aber nicht aufgetaucht.
Definition 2.4.1. Ein Verband (L; ∧, ∨) heiße distributiv, falls für alle a, b, c ∈ L
Folgendes gilt:
(D) a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c) und a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c).
Lemma 2.4.2. Es sei (L; ∩, ∪) ein Teilmengenverband. Dann ist L ein distributiver
Verband.
Beweis. Gemäß Lemma 2.3.5 ist (L; ∩, ∪) ein Verband. Infolge Lemma 2.1.3(v) ist
dieser Verband distributiv.
Anmerkung 2.4.3. Die Ungleichungen
a ∧ (b ∨ c) ≥ (a ∧ b) ∨ (a ∧ c)
a ∨ (b ∧ c) ≤ (a ∨ b) ∧ (a ∨ c)
23
(3)
(4)
gelten in jedem Verband. Daher betrifft Axiom (D) nur die jeweils umgekehrte Ungleichung.
(3) beweist sich folgendermaßen. Gemäß Lemma 2.3.12(ii) folgt aus b ≤ b ∨ c, daß
a ∧ b ≤ a ∧ (b ∨ c); und ebenso gilt a ∧ c ≤ a ∧ (b ∨ c). Gemäß Lemma 2.3.12(i) folgt
(3).
Entsprechend läßt sich auch (4) zeigen.
Wir zeigen weiter, daß von den die Distributivität definierenden (Un)gleichungen sogar
nur eine reicht.
Lemma 2.4.4. Es sei (L; ∧, ∨) ein Verband. Dann ist Folgendes paarweise äquivalent:
(i) L ist distributiv.
(ii) Für alle a, b, c ∈ L gilt
a ∧ (b ∨ c) ≤ (a ∧ b) ∨ (a ∧ c).
(5)
a ∨ (b ∧ c) ≥ (a ∨ b) ∧ (a ∨ c).
(6)
(iii) Für alle a, b, c ∈ L gilt
Beweis. Definitionsgemäß impliziert (i) sowohl (ii) als auch (iii). Mit Blick auf Bemerkung 2.4.3 impliziert (ii) und (iii) zusammengenommen (i). Zu zeigen ist also, daß
(ii) und (iii) äquivalent sind.
Wir zeigen, daß aus (ii) (iii) folgt. Ähnlich ist für die andere Richtung vorzugehen.
Es gelte also (ii). Gemäß Bemerkung 2.4.3 gilt damit die Gleichheit beider Seiten in
(5). Wir rechnen unter zweimaliger Verwendung von (ii)
(a ∨ b) ∧ (a ∨ c) = ((a ∨ b) ∧ a) ∨ ((a ∨ b) ∧ c)
= a ∨ (c ∧ (a ∨ b)
= a ∨ (c ∧ a) ∨ (c ∧ b)
= a ∨ (b ∧ c).
Hier heißt es allerdings aufzupassen: (6) folgt daraus, daß (5) für alle a, b, c eines Verbandes L gilt, und umgekehrt. Gilt hingegen (5) nur für gewisse Elemente a, b, c ∈ L,
heißt dies nicht, daß für diese auch (6) gilt.
Beispiel 2.4.5. Alle in Beispiel 2.3.8 besprochenen Verbänden sind distributiv.
Nichtdistributive Verbände sind erst das Thema ab Kapitel 4. Wir nehmen dennoch
einen Fall vorweg, nur um zu demonstrieren, daß die distributiven Verbände innerhalb
der Verbände eine eher spezielle Teilklasse bilden.
24
Es sei L die Menge aller linearen Unterräume des R2 . L enthält also den 0-dimensionalen
Unterraum {0}; die 1-dimensionalen Unterräume [(r, s)] = {λ(r, s) : λ ∈ R} für
(r, s) ∈ R2 ; und den ganzen Raum R2 . Wir ordnen L durch mengentheoretische Inklusion. Dann ist L ein Verband; das Infimum zweier Unterräume A und B ist deren
Durchschnitt A ∩ B und das Supremum A ∨ B der von A und B aufgespannte Unterraum. Es gilt
[(1, 1)] ∩ ([(1, 0)] ∨ [(0, 1)]) = [(1, 1)] ∩ R2 = [(1, 1)],
aber
([(1, 1)] ∩ [(1, 0)]) ∨ ([(1, 1)] ∩ [(0, 1)]) = {0} ∨ {0} = {0}.
Folglich ist der Verband (L; ∩, ∨) nicht distributiv.
Lemma 2.4.6. Der Unterverband (A; ∧, ∨) eines distributiven Verbandes (L; ∧, ∨) ist
ebenfalls ein distributiver Verband.
Beweis. Gemäß Lemma 2.3.15 ist L ein Verband. Des weiteren gilt die Gleichung (D)
in L, folglich auch in A.
Schließlich stellt sich die Frage, wie man aus einem Hassediagramm herauslesen kann,
ob ein Verband distributiv ist. Es gilt folgendes Lemma.
Lemma 2.4.7. Ein Verband L ist genau dann distributiv, wenn er keinen Unterverband
der folgenden Form enthält:
N5
M3
Beweis. Ausgelassen.
0, 1-Verbände
Null- und Einselement eines Verbandes werden zuweilen zum Teil der Struktur gemacht, d.h. es werden Konstanten hinzugefügt, die durch das Null- bzw. Einselement
interpretiert werden.
Definition 2.4.8. Eine Struktur (L; ∧, ∨, 0, 1) heiße 0, 1-Verband, falls (L; ∧, ∨) ein
Verband ist und 0 das Null- und 1 das Einselement von L ist.
Hat ein Verband kein Null- oder Einselement, läßt sich gemäß Lemma 2.2.14 ein solches hinzufügen. Das Ergebnis ist ein 0, 1-Verband.
25
Satz 2.4.9. Es sei (L; ∧, ∨) ein Verband. L besitze kein Nullelement. Es sei 0 ein neues
˙
Element und L0 = L∪{0};
für a, b ∈ L0 gelte a ≤ b, falls entweder a, b ∈ L ist und
dies in L gilt oder wenn a = 0 ist. Dann ist L0 verbandsgeordnet, und die identische
Abbildung von L nach L0 ist eine Einbettung von Verbänden.
Die entsprechende Konstruktion ist möglich, wenn L kein Einselement besitzt. Schließlich ist auch das gleichzeitige Hinzufügen von Null- und Einselement möglich.
Beweis. Gemäß Lemma 2.2.14 ist (L0 ; ≤) ein Poset. Weiter sei a, b ∈ L0 .
Sind a und b beide in L, ist das in L berechnete Infimum c auch das Infimum in L0 ;
denn in L0 gilt c ≤ a, b, und ist x ≤ a, b, ist x ≤ c unabhängig davon, ob x ∈ L oder
x = 0 ist. Ebenso ist das in L berechnete Supremum auch das Supremum in L0 .
Ist a = 0 oder b = 0, sind a und b gemäß Konstruktion vergleichbar und besitzen
deshalb Infimum wie Supremum. Wir haben gezeigt, daß L0 verbandsgeordnet ist.
Gleichfalls haben wir bewiesen, daß die identische Abbildung L → L0 Infimum und
Supremum erhält. Damit ist der Beweis des ersten Teils komplett.
Fehlt ein Einselement, gehen wir in exakter Analogie vor. Die Konstruktion ist anwendbar auf L ebenso wie auf L0 .
Man beachte, daß im Fall, daß Satz 2.4.9 zum Zuge kommt, der Verband L notwendigerweise unendlich ist; ein endlicher Verband hat immer ein Null- und Einselement.
2.5 Darstellungstheorie
Das grundlegende Beispiel eines distributiven Verbandes ist der Teilmengenverband.
Wir zeigen nun, daß es keine weiteren Beispiele gibt; jeder distributive Verband ist als
Teilmengenverband darstellbar.
Um dies zu zeigen, müssen wir, ausgehend von einem distributiven Verband L, eine
Menge konstruieren und jedes Element von L mit einer Teilmenge identifizieren. Zu
überlegen ist, wie man in einem Teilmengenverband von den Teilmengen zu den einzelnen Elementen der Menge gelangt. Das geht ganz einfach: Man identifiziert jedes
Element der Menge mit dem System dieses enthaltender Teilmengen. Dieses System
ist offenbar unter Durchschnitt und Vergrößerung abgeschlossen und führt uns zu folgender Definition.
Definition 2.5.1. Es sei (L; ∧, ∨) ein Verband. Eine nichtleere Teilmenge F von L
heiße Filter, falls die folgenden Bedingungen gelten:
(F1) Ist a, b ∈ F , so auch a ∧ b ∈ F .
(F2) Ist a ∈ F und b ≥ a, so auch b ∈ F .
Ein Filter F heiße eigentlich, falls F nicht ganz L umfaßt.
Ein eigentlicher Filter F von L heiße Primfilter, falls Folgendes gilt:
26
(F3) Ist für a, b ∈ L a ∨ b ∈ F , gilt entweder a ∈ F oder b ∈ F .
Wir sehen, daß für ein beliebiges Element a eines Verbandes L beispielsweise das System aller Elemente, die größer als a sind, einen Filter bilden; {b ∈ L : b ≥ a} heißt
der Prinzipalfilter von a. Insofern taugt der Begriff des Filters schon einmal, um einzelne Elemente von L zu identifizieren. Der Prinzipalfilter von a ist jedoch nach unten
hin begrenzt; a wird sozusagen nicht weiter aufgesplittet. Dies wiederum ist notwendigerweise der Fall für einen Primfilter; ist a = c ∨ d, muß auch eines der beiden unter a
liegenden Elemente c oder d in F liegen. So können wir in einem Teilmengenverband
mit zugrundeliegender Menge W einen Punkt x ∈ W wählen; dann ist die Menge aller
x enthaltenden Elemente von L ein Primfilter.
In der Tat wollen wir als Grundmenge für den zu konstruierenden Teilmengenverband
die Menge der Primfilter verwenden. Worauf es ankommt, ist zu zeigen, daß es deren
hinreichend viele gibt. Mit Bezug auf einen Teilmengenverband: Sind die zwei verschiedenen Elementen der Grundmenge zugeordneten Primfilter immer verschieden?
Das ist in der Tat der Fall, wenn L distributiv ist, wie Lemma 2.5.4 zeigen wird.
Lemma 2.5.2. Es sei F Filter eines Verbandes L und a ∈ L nicht in F . Dann ist
Fa = {b ∈ L : b ≥ a ∧ f für ein f ∈ F }
der kleinste F und a enthaltende Filter.
Beweis. Ein Filter ist abgeschlossen unter der Bildung von Infima und der Vergrößerung von Elementen. Ein Filter, der F ∪ {a} enthält, muß demzufolge auch Fa enthalten.
Auf der anderen Seite ist Fa ein Filter. Denn ist b, c ∈ Fa , folgt b ≥ a ∧ f1 und
c ≥ a ∧ f2 für f1 , f2 ∈ F und weiter b ∧ c ≥ a ∧ f1 ∧ f2 , d.h. b ∧ c ∈ Fa . Und mit
b ∈ Fa ist zudem klarerweise auch jedes c ≥ b in Fa .
Im weiteren benötigen wir das Zornsche Lemma, welches seinerseits mit dem mengentheoretischen Auswahlaxiom, kurz (AC), gleichwertig ist.
Lemma 2.5.3. (AC) Es sei (P ; ≤) ein Poset mit folgender Eigenschaft: Jeder linear
geordnete Unterposet hat eine obere Schranke. Dann hat P mindestens ein maximales
Element.
Lemma 2.5.4. Es sei F Filter eines distributiven Verbandes L und a ∈ L nicht in F .
Dann gibt es einen Primfilter, der F umfaßt und a nicht enthält.
Beweis. Es sei F die Menge aller Filter von L, die a nicht enthalten. Da F ∈ F , ist F
nicht leer. F wird mittels ⊆ zu einem Poset. Es sei C ⊆ F linear geordnet, d.h. bestehe
aus das Element a nicht enthaltenden
Filtern, so daß je zwei von diesen ineinander
S
S
enthalten sind. Dann ist offenbar C ebenfalls ein Filter, der a nicht enthält; und C
ist eine obere Schranke von C.
27
Folglich können wir Lemma 2.5.3, das Zornsche Lemma, auf den Poset (F ; ⊆) anwenden; es sei P ein maximales Element in F . Da a ∈
/ P , ist P ein eigentlicher Filter. Wir
behaupten, daß P sogar ein Primfilter ist.
Dies zu zeigen, sei c, d ∈ L und c ∨ d ∈ P . Wir nehmen an, daß weder c noch d in P
liegt. P ist maximal in F ; das bedeutet, daß der von P zusammen mit c oder d gemäß
Lemma 2.5.2 erzeugte Filter nicht mehr in F liegt, also a enthält. Nach Lemma 2.5.2
bedeutet a ∈ Pc , daß a ≥ c ∧ f1 für ein f1 ∈ P , und a ∈ Pd , daß a ≥ c ∧ f2 für
ein f2 ∈ P . Aus der Distributivität von L folgt a ≥ (c ∧ f1 ∧ f2 ) ∨ (d ∧ f1 ∧ f2 ) =
(c ∨ d) ∧ f1 ∧ f2 . Da f1 ∧ f2 ∈ P und c ∨ d ∈ P , heißt dies aber a ∈ P . Wir schließen,
daß entweder c oder d in P liegt.
Schließlich geben wir noch folgende Charakterisierungen der Begriffe Filter und Primfilter:
Lemma 2.5.5. Es sei (L; ∧, ∨) ein Verband.
(i) Eine nichtleere Teilmenge F von L ist genau dann ein Filter, wenn Folgendes
gilt: Für alle a, b ∈ L ist a ∧ b ∈ F äquivalent zu a ∈ F und b ∈ F .
(ii) L enthalte ein Nullelement 0. Dann ist ein Filter F von L genau dann eigentlich,
wenn 0 ∈
/ F.
(iii) Ein eigentlicher Filter F von L ist genau dann ein Primfilter, wenn Folgendes
gilt: Für alle a, b ∈ L ist a ∨ b ∈ F äquivalent zu a ∈ F oder b ∈ F .
Beweis. (i) Es sei F ein Filter und a, b ∈ L. Aus a ∧ b ∈ F folgt a, b ∈ F aus (F2).
Aus a, b ∈ F folgt a ∧ b ∈ F aus (F1).
Es sei F ⊆ L, und es gelte a ∧ b ∈ F , gdw a, b ∈ F . (F1) folgt unmittelbar. Ist a ∈ F
und b ≥ a, so ist a ∧ b = a ∈ F und folglich b ∈ F .
(ii) Daß F uneigentlich ist, heißt F = L und insbesondere 0 ∈ F . Gilt 0 ∈ F , folgt
F = L aus (F2).
(iii) Aus a ∈ F oder b ∈ F folgt a ∨ b ∈ F gemäß (F2). Der Rest folgt aus der
Definition eines Primfilters.
Wir kommen zum Darstellungssatz für distributive Verbände.
Satz 2.5.6. Es sei (L; ∧, ∨) ein distributiver Verband. Dann ist L zu einem Teilmengenverband isomorph.
Beweis. Es sei P die Menge aller Primfilter von L. Wir ordnen jedem Element a ∈ L
die Menge aller a enthaltenden Primfilter zu:
ϕ(a) = {P ∈ P : a ∈ P }.
28
(7)
Wir behaupten, daß dies ein Homomorphismus von L in den Verband aller Teilmengen
von P ist. In der Tat ergibt sich für a, b ∈ L unter Verwendung von Lemma 2.5.5:
ϕ(a ∧ b) = {P ∈ P : a ∧ b ∈ P }
= {P ∈ P : a ∈ P und b ∈ P }
= {P ∈ P : a ∈ P } ∩ {P ∈ P : b ∈ P }
= ϕ(a) ∩ ϕ(b)
sowie im Hinblick auf Lemma 2.5.5(iii)
ϕ(a ∨ b) = {P ∈ P : a ∨ b ∈ P }
= {P ∈ P : a ∈ P oder b ∈ P }
= {P ∈ P : a ∈ P } ∪ {P ∈ P : b ∈ P }
= ϕ(a) ∪ ϕ(b)
Weiter ist ϕ injektiv. Denn es seien a, b ∈ L zwei verschiedene Elemente. O.E.d.A. nehmen wir a 6< b an. Dann ist b im Prinzipalfilter von a nicht enthalten; dieser kann nach
Lemma 2.5.4 zu einem b weiterhin nicht enthaltenden Primfilter P erweitert werden.
Also ist P ∈ ϕ(a), aber P ∈
/ ϕ(b).
Es sei nun L′ das Bild von ϕ in der Potenzmenge von P. L′ bildet den Teilmengenverband (L′ ; ∩, ∪), und ϕ, aufgefaßt als Abbildung von L nach L′ , ist ein Isomorphismus.
Leicht läßt sich der Fall ergänzen, daß das Null- und Einselement durch Konstanten
vertreten sind. Enthält ein Teilmengenverband die leere und ganze Menge, bezeichnen
wir diese mit ∅ bzw. r
1.
Satz 2.5.7. Es sei (L; ∧, ∨, 0, 1) ein distributiver 0, 1-Verband. Dann ist L zu einem
Teilmengenverband isomorph, wobei 0 durch die leere und 1 durch die ganze Menge
repräsentiert sind.
Beweis. Gemäß Satz 2.5.6 ist (L; ∧, ∨) isomorph zu einem Teilmengenverband (L′ ; ∩, ∪).
Der Isomorphismus ϕ : L → L′ war durch (7) definiert worden. Wir lesen ab: ϕ(0) =
{P ∈ P : 0 ∈ P } = ∅, weil P nur aus eigentlichen Filtern besteht; s. Lemma 2.5.5(ii).
Weiter gilt: ϕ(1) = {P ∈ P : 1 ∈ P } = P; denn aufgrund Bedingung (F2) enthält
jeder eigentliche Filter 1.
Also ist (L; ∧, ∨, 0, 1) isomorph zu (L′ ; ∩, ∪, ∅,r
1 ).
2.6 Logik
Nach den algebraisch-theoretischen Überlegungen des letzten Abschnitts kehren wir
nunmehr zum ursprünglichen Verständnis distributiver Verbände zurück: Wir fassen
diesen als ein System auf, der gewisse Aussagen repräsentiert.
29
Weiterhin ist das Bild eines Teilmengenverbandes (L; ∩, ∪) maßgeblich. Deren Grundmenge W repräsentiert eine Menge hinsichtlich irgendwelcher Aspekte unterschiedener Situationen; wir hatten W eingangs Menge möglicher Welten genannt. Jedes A ∈ L
ist eine Teilmenge von W und repräsentiert eine Eigenschaft: diejenige Eigenschaft,
die in denjenigen möglichen Welten gilt, die A enthält, und die in den übrigen Welten
nicht gilt.
Es mögen beispielsweise ϕ, ψ, ζ, η vier Eigenschaften symbolisieren. Zu deren Repräsentierung sei eine Menge W möglicher Welten gegeben, und ϕ, ψ, ζ, η seien durch
die Teilmengen A, B, C bzw. D aus L dargestellt. Die Struktur (L; ∧, ∨) bietet nun
zwei Operationen, die es ermöglicht, aus gegebenen Teilmengen neue zu konstruieren, sowie die Möglichkeit, mengentheoretische Inklusion auszudrücken. Aus A und
B wird A ∩ B, welches als die Konjunktion der Eigenschaften ϕ und ψ interpretierbar ist: ϕ und ψ“. Ebenso kann A ∪ B mit der Disjunktion von ϕ und ψ identifiziert
”
werden: ϕ oder ψ“. Weiterhin können Eigenschaften ihrer Ausdruckskraft gemäß zu”
einander in Bezug gesetzt werden. Es gelte in L etwa
A ∩ B ⊆ C ∪ D;
(8)
dies kann interpretiert werden als die Aussage Aus ϕ und ψ folgt, daß ζ oder η“.
”
Diesem Verständnis logischer Zusammenhänge wollen wir nun einen formalen Rahmen verleihen. Wir werden es zu tun haben mit Aussagen wie z.B.
ϕ∧ψ → ζ ∨η
(9)
und diese genau so verstehen wie vorstehend skizzirt: ϕ, ψ, ζ, η werden durch Teilmengen einer fixen Menge modelliert, und (9) wird für gültig erklärt, wenn (8) zutrifft.
Was ist hierbei die Fragestellung? Herausfinden wollen wir, was aus Postulaten von der
Form (9) zu schließen ist. Eine Theorie T wird eine Menge von Implikationen wie (9)
sein; z.B. T = {ϕ → α, ϕ → β}; dann werden wir in der Lage sein, hieraus ϕ →
α ∧ β abzuleiten. Es geht mit anderen Worten darum zu ergründen, welche Schlüsse
aus Zusammenhängen gezogen werden, die in einer Sprache formuliert sind, welche
nichts als das logische und“, das logische oder“ sowie die Implikation enthält – dies
”
”
ist die Sprache der Verbandstheorie.
Wir werden eine spezielle Aussagenlogik definieren. Eine solche konstituiert sich aus
dreierlei:
• Durch die Wahl einer formalen Sprache wird festgelegt, welcher Art Aussagen
betrachtet werden. Die Sprache besteht aus Variablensymbolen, welche beliebige Aussagen bezeichnen, aus Konstantensymbolen, welche bestimmte Aussagen
bezeichnen, sowie aus Verknüpfungssymbolen, mit welchen aus gegebenen Aussagen neue konstruiert werden.
• Weiter wird spezifiert, in welcher Art formalen Strukturen die Aussagen der formalen Sprache zu interpretieren sind. Es handelt sich um Algebren, deren Elemente Aussagen modellieren und die mit Operationen versehen sind, die je eine
Verknüpfung modellieren.
30
• Ein Beweissystem besteht aus Regeln, wie aus in der gewählten formalen Sprache formulierten Aussagen weitere solche generiert werden können. Wenn dabei
erstere unter einer Interpretation in einer Struktur gelten, so muß dies auch für
die abgeleiteten gelten.
Am Beispiel der distributiven 0, 1-Verbände demonstrieren wir nun dieses allgemeine
Schema. Wir spezifieren im Folgenden die Logik distributiver Verbände, abgekürzt
LDV.
Definition 2.6.1. Die Terme der Logik LDV sind die gemäß folgenden Regeln zustandekommenden Zeichenketten.
(i) Eine Variable ist eines der Symbole ϕ1 , ϕ2 , . . .; eine Konstante ist eines der Symbole ⊥, ⊤. Jede Variable und jede Konstante ist ein Term; und zwar ein sogenannt
atomarer Term.
(ii) Sind α und β Terme, so auch α ∧ β und α ∨ β, wobei im Fall, daß α oder β nicht
atomar ist, diese von Klammern zu umschließen sind.
Die Menge aller Terme sei A.
Weiter ist eine Aussage von LDV ein Paar, bestehend aus einer nichtleere endliche
Menge von Termen α1 , . . . , αn sowie einem einzelnen weiteren Term β. Diese notieren
wir gemäß
α1 , . . . , αn → β.
Beispiele für Terme sind etwa ϕ23 , ϕ2 ∧ (ϕ4 ∨ ϕ3 ), ⊥. Beispiele für Aussagen sind
ϕ2 → ϕ5 oder ϕ1 , ϕ2 → ϕ3 ∨ ϕ4 . An letzterer läßt sich die beabsichtigte Bedeutung
einer Aussage demontrieren: Wenn ϕ1 und ϕ2 gilt, so ϕ3 oder ϕ4“. Die logischen
”
Verknüpfungen ∧ und ∨ spiegeln mithin und“ und oder“ wieder; das Komma hat wie
”
”
∧ die Bedeutung und“.
”
Wir legen nun so, wie oben angedeutet, die Interpretation der Aussagen von LDV fest.
Definition 2.6.2. Es sei (L; ∩, ∪, ∅,r
1 ) ein Teilmengenverband. Weiter sei v eine Abbildung von der Menge A aller Terme nach L, so daß folgende Bedingungen erfüllt
sind:
(i) v(⊥) = ∅ und v(⊤) = r
1;
(ii) v(α ∧ β) = v(α) ∩ v(β) und v(α ∨ β) = v(α) ∪ v(β) für alle Terme α, β.
Dann heiße v eine Belegung [engl. evaluation] (der Terme) von LDV. Der Teilmengenverband L heiße dann auch Modell von LDV.
Eine Aussage α1 , . . . , αn → β sei gültig unter einer Belegung v, falls
v(α1 ) ∩ . . . ∩ v(αn ) ⊆ v(β).
31
Eine Belegung ist damit eine Interpretation der Terme der Logik LDV in einem Teilmengenverband. Letzterer wird auf diese Weise zu einem Modell von LDV. Eine Aussage gilt unter einer gegebenen Interpretation, falls der Durchschnitt auf der linken
Seite eine kleinere Menge ergibt als auf der rechten Seite steht; das heißt inhaltlich,
daß die Konjunktion der linken Seite die rechte Seite impliziert.
Zur modelltheoretischen Definition der Logik LDV fehlt nun nur noch die Folgebeziehung.
Definition 2.6.3. Eine Theorie von LDV sei eine Menge von Aussagen von LDV.
Es sei T ein Theorie und Φ eine Aussage von LDV. Wir sagen, daß T Φ semantisch
impliziert, in Zeichen T |= Φ, falls Φ unter jeder Belegung gültig ist, unter der jede
Aussage in T gültig ist.
M.a.W. impliziert eine Menge von Aussagen semantisch eine weitere solche, falls letztere in jedem Modell gilt, in dem jede ersterer gilt.
Damit haben wir festgelegt, was Aussagen von LDV beinhalten und was es heißt, daß
solche andere nach sich ziehen. Die Frage ist nun, ob es Regeln gibt, mit denen man
aus gegebenen Aussagen all diejenigen ableiten kann, die semantisch impliziert sind.
Für LDV ist dies der Fall; wir stellen ein Beweissystem für LDV vor.
Eine Regel ist ein Paar, bestehend aus einer endlichen Menge von Aussagen, den
Prämissen, und einer weiteren Aussage, der Konsequenz. Das Paar wird übereinander
notiert, durch einen horizontalen Strich getrennt. Eine Regel mit leerer Prämissenmenge heißt Axiome; in diesem Fall wird allein die Konsequenz notiert.
Weiter ist die linke Seite einer Aussage stets definitionsgemäß eine nichtleere endliche
Menge; α1 , . . . , αk“ ist die α1 , . . . , αk enthaltende Menge, und Doppeltnennungen
”
sind möglich. Wir werden außer Termen auch Teilmengen von Termen durch Kommata
reihen. Es steht dann z.B. Γ, α, β“ für Γ ∪ {α, β}. Γ kann dabei leer sein, andererseits
”
können α und β auch in Γ enthalten sein.
Definition 2.6.4. Die Regeln von LDV sind die folgenden, worin Γ eine beliebige
endliche Menge von Termen ist und α, β, γ beliebige Terme sind:
(A1) ⊥ → α (A2) α → α (A3) α → ⊤
Γ1 → α Γ2 , α → β
(Cut)
Γ1 , Γ2 → β
Γ, α, β → γ
Γ→α Γ→β
Γ→β
(∧ →)
(→ ∧)
(lw)
Γ, α → β
Γ, α ∧ β → γ
Γ→α∧β
Γ, α → γ Γ, β → γ
Γ→α
Γ→β
(∨ →)
(→ ∨1)
(→ ∨2)
Γ, α ∨ β → γ
Γ →α∨β
Γ→α∨β
Weiter sei T eine Theorie und Φ eine Aussage. Ein Beweis von Φ aus T ist eine endliche Sequenz von Regeln, so daß jeder Prämisse einer Regel entweder aus T oder gleich
der Konsequenz einer vorhergehenden Regel ist und Φ die Konsequenz der letzten Regel ist. Φ heißt aus T beweisbar, in Zeichen T ⊢ Φ, falls es einen Beweis von Φ aus T
gibt.
32
Liegt für eine semantisch begründete Logik ein Beweissystem vor, stellen sich zwei
Fragen. Als wichtigstes ist erstens zu fragen, ob die Regeln korrekt sind: Kann ich mit
den Regeln nur das ableiten, was auch semantisch impliziert ist? Zweitens stellt sich
die manchmal nur akademische, aus Sicht der Logiker aber alles entscheidende Frage,
ob die Regeln vollständig sind: Kann ich mit den Regeln alles ableiten, was semantisch
impliziert ist? Im vorliegenden Fall ist die Antwort zweimal positiv.
Der folgende Satz beinhaltet die sogenannte Korrektheit unseres Beweissystems.
Satz 2.6.5. Es sei T eine Theorie von LDV. Ist Φ aus T beweisbar, so impliziert T Φ
semantisch.
Beweis. Wir müssen für jede Regel Folgendes prüfen: Gelten unter einer Belegung alle
Prämissen, so auch die Konsequenz.
Die drei Axiome müssen demgemäß unter jeder Belegung gelten. Wir betrachten das
Axiom (A1), d.h. ⊥ → α. Dieses gilt unter einer Belegung v, falls v(⊥) ⊆ v(α). v
bildet ⊥ nach ∅ und α in das Element A einer Teilmengenalgebra ab; da ∅ ⊆ A immer
gilt, ist die Bedingung also erfüllt. Ähnlich ist für die übrigen Axiome vorzugehen.
Γ→β
Wir betrachten die Regel (lw), d.h. Γ,α→β
. Es sei Γ = {γ1 , . . . , γk }. Es sei v eine
Belegung; wir setzen G1 = v(γ1 ), . . . , Gk = v(γk ) und A = v(α), B = v(β).
Weiter seien die Prämissen der Regel unter v erfüllt; das bedeutet definitionsgemäß
v(γ1 ) ∩ . . . ∩ v(γk ) ⊆ v(β), d.h.
G1 ∩ . . . Gk ⊆ B.
Hieraus folgt
G1 ∩ . . . Gk ∩ A ⊆ B,
also gilt auch die Konsequenz. Nach dem gleichen Schema ist für die übrigen Regeln
vorzugehen; letztlich sind nur triviale mengentheoretische Fakten benötigt.
Wir kommen nun zur Vollständigkeit unseres Beweissystems. Vollständigkeitsbeweise
können sehr lang und knifflig sein; der vorliegende Fall gibt einen Geschmack davon.
Wir verwenden im Beweis den Begriff der Äquivalenzrelation. Definiert und in aller
Ausführlichkeit besprochen wird dieser jedoch erst in anderem Zusammenhang in Kapitel 4.2. Wer ihn nicht kennt, sei auf Abschnitt 4.2 verwiesen, der sich vom Rest unabhängig lesen läßt; relevant sind hier nur die Definitionen 4.2.1 und 4.2.2 sowie Lemma 4.2.3. Alternativ kann der vorliegende sowie der später noch folgende Vollständigkeitsbeweis beim ersten Lesen auch übersprungen werden.
Satz 2.6.6. Es sei T eine Theorie von LDV. Impliziert T Φ semantisch, so ist Φ aus
T beweisbar.
Beweis. Der Beweis verläuft indirekt. Wir nehmen an, daß Φ aus T nicht beweisbar
ist. Unser Ziel ist es, zu zeigen, daß es eine Belegung gibt, unter alle Elemente von T ,
nicht aber Φ erfüllt ist.
33
Für zwei Terme α und β aus F setzen wir
α∼β
falls
T ⊢ α → β und T ⊢ β → α.
Dann ist ∼ eine Äquivalenzrelation auf F ; Reflexitivität gilt wegen (A1), Symmetrie
nach Konstruktion und Transitivität wegen (Cut). Es sei hαi die Äquivalenzklasse eines
α ∈ F , und es sei hF i = {hαi : α ∈ F }.
Wir behaupten weiter, daß ∼ eine mit ∧ und ∨ kompatible Äquivalenzrelation ist. Das
bedeutet Folgendes:
(⋆) Es sei α, α′ , β, β ′ ∈ F . Aus α ∼ α′ und β ∼ β ′ folgt dann α ∧ β ∼ α′ ∧ β ′ sowie
α ∨ β ∼ α′ ∨ β ′ .
Zum Beweis nehmen wir also α ∼ α′ und β ∼ β ′ an. T beweist dann α → α′ . Es
folgt α, β → α′ mit (lw). Weiter ist β → β Axiom, aus welchem α, β → β folgt. Mit
(→ ∧) ergibt sich α, β → α′ ∧ β und mit (→ ∧) α ∧ β → α′ ∧ β. Entsprechend ist
auch α′ ∧ β → α′ ∧ β ′ herleitbar, und mit (Cut) folgt α ∧ β → α′ ∧ β ′ . Ebenso zeigen
wir, daß T auch α′ ∧ β ′ → α ∧ β beweist; also α ∧ β ∼ α′ ∧ β ′ .
Im Fall von ∨ gehen wir ähnlich vor. Aus α → α′ folgt α → α′ ∨ β mit (→ ∨1). Aus
β → β folgt β → α′ ∨ β mit (→ ∨2). Also α ∨ β → α′ ∨ β mittels (∨ →). Nach
Wiederholung dieser Schritte gelangen wir schließlich zu α ∨ β ∼ α′ ∨ β ′ .
Wir nutzen nun (⋆) aus, um die Operationen ∧ und ∨ auf hF i wie folgt zu erklären.
Für α, β ∈ F setzen wir
hαi ∧ hβi = hα ∧ βi,
hαi ∨ hβi = hα ∨ βi.
Damit haben wir eine Algebra (hF i; ∧, ∨, h0i, h1i) konstruiert. Wir zeigen, daß diese
ein distributiver Verband ist.
Zunächst statten wir hF i mit der Relation
hαi ≤ hβi,
falls T ⊢ α → β
aus. Dann ist ≤ eine partielle Ordnung; Reflexivität gilt wegen (A1), Antisymmetrie
nach Konstruktion und Transitivität wegen (Cut).
Wir zeigen als nächstes, daß ∧ und ∨ in bezug auf ≤ Infimums- und Supremumsoperation sind. Es gilt hα ∧ βi ≤ hαi, hβi; dies zeigt im ersteren Fall der Beweis
α → α (lw)
α, β → α
(∧→)
α ∧ β → α,
der letztere Fall geht analog. Weiter sei hγi ≤ hαi, hβi angenommen; das bedeutet,
daß T γ → α und γ → β beweist. Es folgt γ → α ∧ β, d.h. hγi ≤ hα ∧ βi.
Ähnlich gilt hαi, hβi ≤ hα ∨ βi, und aus hαi, hβi ≤ hγi folgt hα ∨ βi ≤ hγi. Damit
ist gezeigt, daß (hF i; ∧, ∨) ein Verband ist.
34
Wegen (A1) und (A3) sind h⊥i und h⊤i Null- und Einselement. Es verbleibt, das Distributivgesetz nachzuweisen. Wir gehen wie folgt vor:
β→β
α → α (lw)
α, β → α
α, β → β
α, β → α ∧ β
α, β → (α ∧ β) ∨ (α ∧ γ)
(lw)
(→∧)
(→∨)
Ähnlich sehen wir α, γ → (α ∧ β) ∨ (α ∧ γ). Es folgt α, β ∨ γ → (α ∧ β) ∨ (α ∧ γ)
und schließlich α ∧ (β ∨ γ) → (α ∧ β) ∨ (α ∧ γ). Im Hinblick auf Lemma 2.4.4 ist der
Beweis komplett.
Wir definieren nun
v ′ : F → hF i, α 7→ hαi.
Dann ist v ′ (⊥) = h⊥i und v ′ (⊤) = h⊤i, und es gilt v ′ (α ∧ β) = v ′ (α) ∧ v ′ (β) sowie
v ′ (α∨β) = v ′ (α)∨v ′ (β). Schließlich ist der distributive Verband (hF i; ∧, ∨, h0i, h1i)
einem Teilmengenverband isomorph. Ist ϕ der Isomorphismus, ist v = ϕ ◦ v ′ eine
Belegung.
Es sei weiter α1 , . . . , αk → β eine Aussage aus T . Diese ist trivialerweise aus T
beweisbar und damit auch α1 ∧ . . . ∧ αk → β. Dies bedeutet wiederum v ′ (α1 ) ∧ . . . ∧
v(αk ) = hα1 i ∧ . . . ∧ hαk i = hα1 ∧ . . . ∧ αk i ≤ hβi = v ′ (β). Also ist die Aussage
unter v erfüllt.
Weiter sei Φ die Aussage γ1 , . . . , γl → δ. Wäre Φ unter v erfüllt, hieße dies hγ1 ∧ . . . ∧ γl i =
hγ1 i ∧ . . . ∧ hγl i = v(γ1 ) ∧ . . . ∧ v(γl ) ≤ v(δ) = hδi; also wäre Φ aus T beweisbar.
Es folgt, daß Φ unter v nicht erfüllt ist.
35
3 Boolesche Algebren
3.1 Motivation
Ein weiteres Mal gehen wir davon aus, daß wir eine Menge von Situationen zu modellieren haben, repräsentiert durch eine Menge möglicher Welten W . Mögliche Welten
sind durch Eigenschaften charakterisiert, die in jeder solchen entweder zutreffen oder
nicht. Ja-Nein-Aussagen besagen, daß eine gewisse Eigenschaft zutrifft. Eine Aussage
ϕ wird demgemäß durch eine Teilmenge von W modelliert, etwa A; eine mögliche
Welt ist in A genau denn, wenn die ϕ zugeordnete Eigenschaft in dieser möglichen
Welt zutrifft.
Wir haben Aussagen ihrer Stärke nach verglichen. Es sei etwa ϕ durch A und ψ durch
B modelliert. Dann kann A in B enthalten sein; in diesem Fall ist ϕ die stärkere der
beiden Aussagen und ψ die schwächere; in der Tat gilt ψ in allen möglichen Welten, in
dene ϕ gilt, und in diesem Sinne impliziert ϕ ψ. Die zugehörige abstrakte Struktur ist
die eines Posets.
Mittels der partiellen Ordnung kann man weiter je zwei Aussagen deren Konjunktion
zuordnen. Als Konjunktion können wir die schwächste Aussage ansehen, die stärker
ist als beide diese Aussagen; im Poset ist dies das Infimum der beiden Teilmengen von
W , der mengentheoretische Durchschnitt von A und B, d.h. A ∩ B. Als Disjunktion
können wir die stärkste Aussage ansehen, die schwächer ist als ϕ und ψ; es ergibt sich
das Supremum, die Vereinigung von A und B, d.h. A ∪ B.
Wir haben die Negation von Aussagen bislang noch nicht betrachtet. Nahe liegt, wenn
ϕ durch A repräsentiert wird, die Negation von ϕ durch das mengentheoretische Komplement darzustellen, d.h. ∁A. Genau dies werden wir im weiteren tun. Man beachte,
daß damit das Gebiet der Posets nicht verlassen; so wie das Infimum und das Supremum ist auch das Komplement allein durch die partielle Ordnung festgelegt. Die Negation von ϕ ist die schwächste Aussage, deren Konjunktion mit ϕ die falsche Aussage
ist; demgemäß wird sie durch die größte Menge modelliert, deren Durchschnitt mit A
die leere Menge ergibt – dies ist ∁A.
Wenn wir die so verstandene Negation hinzufügen, gelangen wir vom distributiven
0, 1-Verband zur booleschen Algebra.
Definition 3.1.1. Es sei W eine nichtleere Menge. Weiter bestehe L aus Teilmengen
von W dergestalt, daß ∅ und r
1 = W , mit A jeweils auch ∁A und mit A und B jeweils
auch A ∩ B und A ∪ B in L ist. Dann heiße (L; ∩, ∪, ∁, ∅,r
1 ) eine Teilmengenalgebra.
Insbesondere kann L die ganze Potenzmenge PW von W sein.
Wir listen im Folgenden die charakteristischen Eigenschaften einer Teilmengenalgebra
auf.
Lemma 3.1.2. Es sei (L; ∩, ∪, ∁, ∅,r
1 ) eine Teilmengenalgebra. Dann gilt für alle
A, B, C ∈ L:
(0) ∅ ⊆ A und A ⊆ r
1.
36
(i) A ∩ A = A ∪ A = A.
(ii) A ∩ B = B ∩ A und A ∪ B = B ∪ A.
(iii) A ∩ (B ∩ C) = (A ∩ B) ∩ C und A ∩ (B ∪ C) = (A ∪ B) ∪ C.
(iv) A ∩ (A ∪ B) = A ∪ (A ∩ B) = A.
(v) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) und A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
(vi) A ∩ ∁A = ∅ und A ∪ ∁A = r
1.
3.2 Komplemente in Verbänden
Wir halten uns für die folgenden Definitionen die Teilmengenalgebra vor Augen.
Definition 3.2.1. Es sei (L; ∧, ∨, 0, 1) ein 0, 1-Verband. Es sei a ∈ L. Dann heiße
b ∈ L Komplement von a falls
(i) a ∧ b = 0,
(ii) a ∨ b = 1
gilt. Besitzt jedes a ∈ L ein Komplement, heiße L komplementiert.
Eine Funktion ¬ : L → L heiße eine Komplementfunktion von L, falls für alle a, b ∈ L
Folgendes gilt:
(CF1) ¬a ist ein Komplement von a,
(CF2) aus a ≤ b folgt ¬b ≤ ¬a,
(CF3) ¬¬a = a.
Man könnte vielleicht meinen, daß Komplemente, wenn vorhanden, eindeutig bestimmt
sind oder zumindest jedes Element ein kanonisches Komplement hat. Dies gilt für distributive Verbände, keinesfalls aber allgemein.
Beispiel 3.2.2.
(i) Es sei (L; ∩, ∪, ∅,r
1 ) ein Teilmengenverband mit 0 und 1. Dann
ist L komplementiert. Wie man sich leicht überlegt, hat jedes A ∈ L genau ein
Komplement, und zwar ∁A. Zudem ist L → L, A 7→ ∁A eine Komplementfunktion.
(ii) Ein linear geordnete Menge mit mehr als zwei Elementen ist nicht komplementiert. Man betrachte z.B. die vierelementige Menge {0, 1, 2, 3} mit ≤ als der
natürlichen Ordnung. Es hat 1 kein Komplement; x ∧ 1 = 0 impliziert x = 0,
wohingegen x ∨ 1 = 3 x = 3 bedeutet.
(iii) Der Verband M3 (s. Beispiel 2.2.13) ist komplementiert. Die nichtextremalen
Elemente haben je zwei Komplemente. Z.B. besitzt b das Komplement c und d.
Eine Komplementfunktion läßt sich auf M3 jedoch nicht definieren.
37
Der Begriff des Komplementes läßt sich wie folgt auch lokal definieren. In einem Teilmengenverband können wir etwa eine Menge herausgreifen, das Intervall betrachten,
das aus deren Teilmengen besteht, und danach fragen, ob Teilmengen innerhalb dieses
Intervalls Komplemente besitzen.
Definition 3.2.3. Es sei (L; ∧, ∨) ein Verband. Es sei p, q ∈ L mit p < q, und es sei
a ∈ [p, q]. Dann heiße b ∈ L relatives Komplement von a in [p, q], falls
(i) a ∧ b = p,
(ii) a ∨ b = q
gilt. Besitzt jedes a ein relatives Komplement in jedem a enthaltenden Intervall, heiße
L relativ komplementiert.
Dies läßt sich auch so ausdrücken: In einem Verband sei p ≤ a ≤ q; dann heißt
für b, ein relatives Komplement von a im Intervall [p, q] zu sein, ein Komplement im
normalen Sinne im 0, 1-Verband ([p, q]; ∧, ∨, p, q) zu sein.
Lemma 3.2.4. Ein Verband L ist relativ komplementiert genau dann, wenn jedes Intervall von L komplementiert ist.
Beweis. Dies ist aus den Definitionen unmittelbar einsichtig.
In distributiven Verbänden können wir aus Komplementen leicht auch relative Komplemente bestimmen.
Lemma 3.2.5. Es sei (L; ∧, ∨) ein distributiver Verband. Es sei b ∈ L Komplement
von a ∈ L. Weiter sei p < q und a ∈ [p, q]. Dann ist
b′ = (b ∧ q) ∨ p
(10)
relatives Komplement von a in [p, q].
Beweis. Dies überprüfen wir durch Nachrechnen der Bedingungen (i), (ii) aus Definition 3.2.3.
Beispiel 3.2.6.
(i) Es sei (L; ∩, ∪, ∅,r
1 ) ein Teilmengenverband mit 0 und 1. Es
seien P, Q ∈ L mit P ⊂ Q und A ∈ L mit P ⊆ A ⊆ Q gegeben.
Hat A das relative Komplement B in [P, Q], muß A ∩ B = P und A ∪ B = Q
gelten. Also ist (∁A∩Q)∪P = (∁A∩(A∪B))∪(A∩B) = (∁A∩∩B)∪(A∩B) =
B. Damit ist (10) bestätigt.
(ii) Der folgende Verband L ist komplementiert. Jedoch hat das Element c im Intervall [b, d] kein relatives Komplement:
38
L
3.3 Boolesche Algebren
Wir betrachten nunmehr Komplementfunktionen auf distributiven Verbänden.
Definition 3.3.1. Eine Algebra (L; ∧, ∨, ¬, 0, 1) heiße boolesche Algebra, falls Folgendes gilt:
(BA1) (L; ∧, ∨, ¬, 0, 1) ist ein distributiver 0, 1-Verband.
(BA2) ¬ ist eine Komplementfunktion auf L.
Boolesche Algebren sind insbesondere komplementierte distributive Verbände. Boolesche Algebren und komplementierte distributive Verbände sind im Grunde sogar dasselbe, wie das folgende Lemma zeigt.
Lemma 3.3.2. Es sei (L; ∧, ∨, 0, 1) ein komplementierter distributiver 0, 1-Verband.
Dann besitzt jedes a genau ein Komplement ¬a, und zwar
¬a = max {c ∈ L : a ∧ c = 0}.
(11)
Es gibt zudem genau eine Komplementfunktion auf L, gegeben durch die Zuordnung
a 7→ ¬a. Mit dieser ist (L; ∧, ∨, ¬, 0, 1) eine boolesche Algebra.
Beweis. Es sei a ∈ L. Nach Voraussetzung besitzt a das Komplement b. Da a ∧ b = 0,
ist b in der Menge {c ∈ L : a ∧ c = 0} enthalten, welche damit insbesondere nicht leer
ist. Angenommen sei, daß a ∧ c = 0 für ein c ∈ L. Dann folgt c = c ∧ 1 = c ∧ (a ∨ b) =
(c ∧ a) ∨ (c ∧ b) = c ∧ b ≤ b. Also ist b das größte Element von {c ∈ L : a ∧ c = 0}.
Es folgt (11) und insbesondere, daß a genau ein Komplement besitzt.
Wir zeigen, daß (11) eine Komplementfunktion definiert; dann folgt, daß L, erweitert
um die Operation ¬, eine boolesche Algebra ist. Nachzuprüfen sind (CF2) und (CF3).
Ist a ≤ b, folgt {c ∈ L : b ∧ c = 0} ⊆ {c ∈ L : a ∧ c = 0}, also ist das Maximum über
letztere Menge größer als das über die erstere, d.h. ¬b ≤ ¬a. Ist weiter b Komplement
von a, so ist auch a Komplement von b; wegen der Eindeutigkeit des Komplements
folgt ¬¬a = a.
Damit ist formal gezeigt, daß die Komplementfunktion boolescher Algebra durch die
partielle Ordnung allein schon eindeutig bestimmt ist.
Lemma 3.3.3. Eine Teilmengenalgebra (L; ∩, ∪, ∁, ∅,r
1 ) ist eine boolesche Algebra.
39
Beweis. Gemäß Lemma 2.3.5 ist (L; ∩, ∪) ein Verband. Gemäß Lemma 3.1.2(0) ist ∅
das Null- undr
1 das Einselement. Gemäß 3.1.2(vi) ist ∁A ein Komplement eines A ∈ L.
Also ist L ein komplementierter distributiver 0, 1-Verband, gemäß Lemma 3.3.2 also
eine boolesche Algebra.
Beispiel 3.3.4. Über das Standardbeispiel hinaus weitere Beispiele zu geben ist gar
nicht einfach.
(i) Der einfachste Fall von Lemma 3.3.3 ist die ganze Potenzmenge einer Menge
W . Das folgende ist ein Beispiel, wo nicht die ganze Potenzmenge zum Einsatz
kommt.
Es sei W eine unendliche Menge. Es sei Wf = {A ⊆ W : A ist endlich} die
Menge aller endlichen und Wcf = {A ⊆ W : ∁A ist endlich} die Menge aller
sogenannt koendlichen Teilmengen von W . Dann überlegt man sich leicht, daß
L = Wf ∪Wcf die leere und ganze Menge enthält und unter Durchschnitt, Vereinigung sowie Komplementbildung abgeschlossen ist. Also ist (L; ∩, ∪, ∁, ∅,r
1)
eine Teilmengenalgebra, insbesondere eine boolesche Algebra.
(ii) Es sei W ein topologischer Raum und es sei L die Menge aller regulär offenen
Mengen:
L = {A◦ : A ⊆ W ist abgeschlossen }.
Beispielsweise sei W = R mit der üblichen Topologie versehen. Dann sind
offene Intervalle in L und auch deren Vereinigungen, sofern die Randpunkte
nicht übereinstimmen. D.h. (0, 1) ∪ (2, 3) liegt in L, (0, 1) ∪ (1, 2) aber nicht;
(0, 1) ∪ (1, 2) ist nicht das offene Innere irgendeiner abgeschlossenen Menge.
Für A ⊆ W setzen wir
◦
Ar = A− .
Wir behaupten, daß Ar r = A für jedes A ⊆ W gilt. Hierfür berechnen wir
Ar = {x ∈ W : es gibt eine Umgebung U von x, so daß U ⊆ A− }
= {x ∈ W : es gibt eine Umgebung U von x, so daß
für jede Umgebung V eines beliebigen y ∈ U gilt V ∩ A 6= ∅}
= {x ∈ W : es gibt eine Umgebung U von x, so daß
für jedes nichtleere offene V ⊆ U gilt V ∩ A 6= ∅}.
Es folgt, da Ar offen ist, daß
Ar r = {x ∈ W : es gibt eine Umgebung U von x, so daß
für jedes nichtleere offene V ⊆ U gilt V ∩ Ar 6= ∅}
= {x ∈ W : es gibt eine Umgebung U von x, so daß U ⊆ Ar gilt}
= Ar .
Wir behaupten weiter, daß eine Teilmenge A ⊆ W genau dann regulär ist, wenn
A = Ar . Denn aus A = Ar folgt natürlich die Regularität von A. Umgekehrt
40
sei A regulär, d.h. A = B ◦ für ein abgeschlossenes B ⊆ W . Dann folgt Ar =
B ◦ r = B r r = B r = B ◦ = A.
Als nächstes bemerken wir, daß für offene Mengen A, B ⊆ W gilt
Ar ∩ B r = (A ∩ B)r .
Denn, wie wir wissen, gilt
Ar ∩ B r = {x ∈ W : es gibt eine Umgebung U von x, so daß
für jedes nichtleere offene V ⊆ U gilt V ∩ A, V ∩ B 6= ∅}.
Für ein x sei U eine Umgebung wie spezifiziert. Dann gilt für jdees offene V ⊆
U , daß V ∩ A 6= ∅; und da auch V ∩ A offen ist, gilt auch V ∩ A ∩ B 6= ∅. Es
folgt
Ar ∩ B r = {x ∈ W : es gibt eine Umgebung U von x, so daß
für jedes nichtleere offene V ⊆ U gilt V ∩ A ∩ B 6= ∅}
= (A ∩ B)r .
L sei nun durch ⊆ partiell geordnet. Wir behaupten, daß dann L ein Verband ist.
Denn für reguläre Mengen A, B ∈ L ist
A ∩ B = Ar ∩ B r
= (A ∩ B)r
wiederum regulär; also ist A ∩ B das Infimum von A und B in L. Die Vereinigung zweier regulärer Mengen ist i.a. nicht regulär; das Supremum von A und B
existiert dennoch:
A ∨ B = (A ∪ B)r .
In der Tat folgt aus A ⊆ A ∪ B, daß A = Ar ⊆ (A ∪ B)r gilt; ähnlich folgt
B ⊆ (A ∪ B)r ; also ist (A ∪ B)r obere Schranke von A und B. Ist weiter C ∈ L
und A, B ⊆ C, folgt A ∪ B ⊆ C und weiter (A ∪ B)r ⊆ C r = C.
1)
Klarerweise sind ∅ undr
1 = W regulär. Wir haben mithin gezeigt, daß (L; ∩, ∨, ∅,r
ein 0, 1-Verband ist.
Dieser ist sogar distributiv. Es seien A, B, C ∈ L:
A ∩ (B ∨ C) = Ar ∩ (B ∪ C)r
= (A ∩ (B ∪ C))r
= ((A ∩ B) ∪ (A ∩ C))r
= (A ∩ B) ∨ (A ∩ C)
Schließlich zeigen wir, daß für jedes A ∈ L
◦
¬A = (∁A)
41
ein Komplement von A in L ist. Gemäß Lemma 3.3.2 ist somit ¬ eine Komplementfunktion und (L; ∩, ∨, ¬, ∅,r
1 ) eine boolesche Algebra.
Zunächst ist klar, daß ¬A als offenes Innere einer abgeschlossenen Menge in L
liegt. Weiter gilt
◦
¬A ∩ A = (∁A) ∩ A
= (∁A)r ∩ Ar
= (∁A ∩ A)r
= ∅
sowie
(¬A ∪ A)
−
−
◦
= ((∁A) ∪ A)
◦−
= (∁A)
∪ A−
◦
= ∁A− ∪ A−
= ∁A ∪ A−
=r
1
und damit ¬A ∨ A = (¬A ∪ A)r = r
1.
Wie im Fall der Verbände fragen wir als nächstes, wie sich boolesche Algebren ohne
Rückgriff auf die partielle Ordnung, vielmehr nur durch Gleichungen im Stil von Satz
2.3.6 definieren lassen.
Satz 3.3.5. Eine Algebra (L; ∧, ∨, ¬, 0, 1) ist eine boolesche Algebra genau dann,
wenn für alle a, b, c ∈ L die Bedingungen (V1) bis (V4), (D) sowie Folgendes gilt:
(V5) 0 ∧ a = 0 und 1 ∨ a = 1.
(K) a ∧ ¬a = 0 und a ∨ ¬a = 1.
Beweis. Ist L eine boolesche Algebra, ist definitionsgemäß (L; ∧, ∨, 0, 1) ein distributiver 0, 1-Verband mit der Komplementfunktion ¬. Es folgt die eine Richtung der
Behauptung.
Es sei (L; ∧, ∨, ¬, 0, 1) eine Algebra, die (V1) bis (V5), (D) und (K) erfüllt. Dann ist
(L; ∧, ∨) nach Satz 2.3.6 ein Verband; dieser ist wegen (D) distributiv. Weiter sind 0
und 1 wegen (V5) Null- und Einselement. Schließlich ist L wegen (K) komplementiert
und ordnet ¬ jedem a ein Komplement zu; gemäß Satz 3.3.2 ist (L; ∧, ∨, ¬, 0, 1) damit
eine boolesche Algebra.
3.4 Darstellungstheorie
Wir zeigen nun, daß sich jede boolesche Algebra durch eine Teilmengenalgebra darstellen läßt.
42
Satz 3.4.1. Es sei (L; ∧, ∨, ¬, 0, 1) eine boolesche Algebra. Dann ist L zu einer Teilmengenalgebra isomorph.
Beweis. (L; ∧, ∨, 0, 1) ist ein distributiver 0, 1-Verband. Nach Satz 2.5.7 ist dieser einem Teilmengenverband (L′ ; ∩, ∪, ∅,r
1 ) isomorph. Es sei ϕ : L → L′ der Isomorphismus.
Es verbleibt zu zeigen, daß ϕ(¬a) = ∁ϕ(a) für alle a ∈ L gilt. Man rekapituliere, daß
im Beweis von Satz 2.5.6 ϕ durch (7) definiert war.
Wir behaupten, daß für jeden Primfilter P und jedes a ∈ L ¬a ∈ F genau dann gilt,
wenn a ∈
/ P gilt. Es sei ¬a ∈ P ; dann hieße a ∈ P , daß 0 = a ∧ ¬a ∈ P und P = L,
also P uneigentlich wäre, ein Widerspruch. Es sei a ∈
/ P . Aus a ∨ ¬a = 1 ∈ P und
Lemma 2.5.5(iii) folgt, daß entweder a ∈ P oder ¬a ∈ P ist; es folgt ¬a ∈ P .
Daraus ergibt sich
ϕ(¬a) = {P ∈ P : ¬a ∈ P }
= {P ∈ P : a ∈
/ P}
= ∁{P ∈ P : a ∈ P }
= ∁ϕ(a).
3.5 Logik
Wie im Fall distributiver Verbände wenden wir uns der ursprünglichen Motivation zu,
aus der heraus wir die in diesem Abschnitt besprochenen Algebren untersucht haben:
Boolesche Algebren stehen für Systeme von Aussagen.
Wir gehen diesmal von einer Teilmengenalgebra (L; ∩, ∪, ¬, ∅,r
1 ) aus. Jedes A ∈
L repräsentiert eine Eigenschaft und enthält diejenigen möglichen Welten, in der die
Eigenschaft gilt. Die Verknüpfung zweier Eigenschaften durch ein und“ wird durch
”
die Durchschnittsbildung der modellierenden Teilmengen realisiert, die Verknüpfung
oder“ durch die Vereinigungsbildung. Die leere Menge repräsentiert die nie, die ganze
”
Menge die immer zutreffende Eigenschaft.
Im Fall boolescher Algebren kommt neu hinzu die Negation. Es vertrete ϕ eine Eigenschaft. Wir legen fest, daß diejenige Eigenschaft, die genau dann gilt, wenn ϕ nicht gilt,
durch das Komplement von A zu modellieren. Wird also ϕ durch A ∈ L modelliert, so
nicht ϕ“ durch ∁A.
”
Von dieser Ergänzung abgesehen gehen wir im Folgenden exakt genauso vor wie im
Fall distributiver Verbände. Wir spezifizieren nunmehr die Klassische Aussagenlogik,
abgekürzt KAL.
Definition 3.5.1. Die Terme der Logik KAL sind die gemäß den für LDV geltenden
Regeln aus Def. 2.6.1 (i), (ii) zustandekommenden Zeichenketten mit einem Zusatz:
43
(iii) Ist α ein Term, so auch ¬α, wobei α im Fall, daß es sich nicht um einen atomaren
Term handelt, von Klammern zu umschließen ist.
Die Menge aller Terme sei A. Ausgehend von den Termen von KAL sind Aussagen von
KAL wie im Fall LDV erklärt.
Aussagen von KAL werden wie folgt interpretiert.
Definition 3.5.2. Es sei (L; ∩, ∪, ∁, ∅,r
1 ) eine Teilmengenalgebra. Weiter sei v eine
Abbildung von der Menge A aller Terme nach L, so daß folgende Bedingungen erfüllt
sind:
(i) v(⊥) = ∅ und v(⊤) = r
1;
(ii) v(α ∧ β) = v(α) ∩ v(β), v(α ∨ β) = v(α) ∪ v(β) und v(¬α) = ∁v(α) für alle
Terme α, β.
Dann heiße v eine Belegung von KAL.
Eine Aussage α1 , . . . , αn → β sei gültig unter einer Belegung v, falls
v(α1 ) ∩ . . . ∩ v(αn ) ⊆ v(β).
Schließlich wird auch die semantische Folgebeziehung für KAL genauso wie für LDV
erklärt.
Definition 3.5.3. Eine Theorie von KAL sei eine Menge von Aussagen von KAL.
Es sei T ein Theorie und Φ eine Aussage von KAL. Wir sagen, daß T Φ semantisch
impliziert, in Zeichen T |= Φ, falls Φ unter jeder Belegung gültig ist, unter der jede
Aussage in T gültig ist.
Nach der Spezifikation von KAL wenden wir uns nun der Frage nach einem Beweissystem zu. Es stellt sich heraus, daß es genügt, die Regeln von LDV um zwei zu ergänzen,
die die neu hinzugekommene Negation betreffen.
Definition 3.5.4. Die Regeln von KAL sind diejenigen von LDV und zusätzlich die
folgenden, worin Γ eine beliebige endliche Menge von Termen ist und α, β, γ beliebige
Terme sind:
(A4) α, ¬α → ⊥ (¬1 )
Γ, α → ⊥
Γ → ¬α
(¬2 )
Γ, ¬α → ⊥
Γ→α
Die Begriffe des Beweises und der Beweisbarkeit sind für KAL in der gleichen Weise
definiert wie für LDV.
Wir wenden uns der Frage der Korrektheit und Vollständigkeit zu.
Erstere ist wieder einfach und wird nicht weiter ausgeführt.
Satz 3.5.5. Es sei T eine Theorie von KAL. Ist Φ aus T beweisbar, so impliziert T Φ
semantisch.
44
Beweis. Das Vorgehen ist das gleiche wie im Fall von Satz 2.6.5.
Für letztere müssen wir lediglich den Beweis von Satz 2.6.6 etwas erweitern.
Satz 3.5.6. Es sei T eine Theorie von KAL. Impliziert T Φ semantisch, so ist Φ aus
T beweisbar.
Beweis. Wir nehmen an, daß Φ aus T nicht beweisbar ist. Wie im Beweis von Satz
2.6.6 konstruieren wir hF i.
Dort war gezeigt, daß ∼ eine mit ∧ und ∨ kompatible Äquivalenzrelation ist. Wir
zeigen, daß ∼ darüberhinaus auch mit ¬ kompatibel ist. Das bedeutet:
(⋆⋆) Es sei α, α′ ∈ F . Aus α ∼ α′ folgt dann ¬α ∼ ¬α′ .
Wir nehmen also α ∼ α′ . T beweist dann α → α′ , also auch α, ¬α′ → ⊥ und weiter
¬α′ → ¬α. Ähnlich sehen wir ¬α → ¬α′ , und es folgt ¬α ∼ ¬α′ .
Wir erklären nun die Operationen ∧ und ∨ auf hF i wie gehabt und ¬ gemäß
¬hαi = h¬αi
für α ∈ F . Wir behaupten, daß die Algebra (hF i; ∧, ∨, ¬, h0i, h1i) eine boolesche
Algebra ist. Bereits gezeigt war, daß (hF i; ∧, ∨, h0i, h1i) ein distributiver 0, 1-Verband
ist. Es verbleibt nachzuweisen, daß für jedes α ∈ F ¬hαi ein Komplement von hαi in
hF i ist.
Es sei α ∈ F . Aus (A4) folgt α ∧ ¬α → ⊥; umgekehrt gilt ⊥ → α ∧ ¬α gemäß (A1).
Somit ist hα ∧ ¬αi = h⊥i.
Weiter läßt sich α → α ∨ ¬α sowie ¬α → α ∨ ¬α beweisen. Durch Anwendung
von (¬1 ) folgt weiter ¬(α ∨ ¬α) → ¬α sowie ¬(α ∨ ¬α) → ¬¬α und aus beidem
zusammen ¬(α ∨ ¬α) → ¬α ∧ ¬¬α. Wir hatten bereits gezeigt, daß ¬α ∧ ¬¬α → ⊥,
und es folgt ¬(α ∨ ¬α) → ⊥ und weiter ¬⊥ → ¬¬(α ∨ ¬α). Mit (¬1 ) ist ⊤ → ¬⊥
beweisbar; weiter ist ¬¬(α ∨ ¬α), ¬(α ∨ ¬α) → ⊥ und damit ¬¬(α ∨ ¬α) → α∨¬α
beweisbar. Somit folgt schließlich ⊤ → α ∨ ¬α. Da ohnehin α ∨ ¬α → ⊤ Axiom ist,
ist hα ∨ ¬αi = h⊤i gezeigt.
Die verbleibende Argumentation ist wiederum wie im Beweis von Satz 2.6.6.
45
4 Äquivalenzrelationen und Partitionsverbände
4.1 Motivation
Verbände sind spezielle partielle geordnete Mengen; eine partielle Ordnung drückt auf
einem Grundbereich ein Mehr oder Weniger“, ein Umfassen oder Enthaltensein“,
”
”
ein Stärker oder Schwächer“ aus. Unser prototypisches Beispiel war ein System von
”
Teilmengen einer fix gegebenen Menge; betrachtet haben wir die Relation, daß eine
Teilmenge in einer anderen enthalten war.
Wir gehen auch im Folgenden von einer fix gegebenen Menge und deren Teilmengen
aus, steigen nunmehr aber sozusagen in der Betrachtung eine Ebene höher“. Wir be”
trachten nicht mehr einzelne Teilmengen der ganzen Menge; wir betrachten einzelne
Arten, die ganze Menge, sagen wir wieder W , in Teilmengen aufzuteilen. Eine Partition besteht aus paarweise disjunkten Teilmengen, Blöcke genannt, die zusammen
ganz W ergeben. Was vorher eine einzelne Teilmenge unserer Grundmenge war, ist
nunmehr ein einzelne Partition. Wir betrachten unterschiedliche Partitionen auf derselben Grundmenge, und wir führen auf der Menge der Partitionen eine partielle Ordnung
ein: eine gegebene Partition kann feiner sein als eine andere, indem erstere aus letzterer
dadurch hervorgeht, daß die Blöcke letzterer noch weiter unterteilt werden.
Um uns ein intuitives Bild von der Aufgabe zu machen, die wir im Folgenden angehen,
können wir von folgendem Bild ausgehen. Es sei eine Menge irgendwelcher Objekte
gegeben; diese Menge W darf mit einer Menge möglicher Welten identifiziert werden. Eine Partition von W kann dann als eine Art und Weise angesehen werden, die
gegebenen Objekte zu klassifizieren.
Beispielsweise sei jedes Objekt durch drei reelle Parameter beschreibbar; wir wählen
demgemäß W = R3 . Wir können nun zu einer gröberen Klassifizierung übergehen,
z.B. zu derjenigen, die nur den einen der drei Parameter berücksichtigt. Wir betrachten
also die Gruppen derjenigen Objekte, deren i-ter Parameter übereinstimmt, i = 1, 2, 3.
Für i = 1 ergibt sich die Partition
R3 =
[
˙
x1 ∈R
{(x1 , x2 , x3 ) : x2 , x3 ∈ R}.
Ṡ
Für i = 2 erhalten wir R3 = y∈R {(x1 , x2 , x3 ) : x1 , x3 ∈ R} und können fragen:
Welches ist die gröbste Unterteilung von R3 , welche beide diese Partitionen enthält?
Oder auch umgekehrt: Welches ist die feinste Unterteilung von R3 , welche beide dieṠ
se Partitionen enthalten? Die Antworten: R3 = x1 ,x2 ∈R {(x1 , x2 , x3 ) : x3 ∈ R} ist
die gröbste gemeinsame Verfeinerung; zwei Objekte werden genau dann unterschieden und sind gementsprechend in verschiedenen Klassen, wenn sie sich entweder in
bezug auf die erste oder die zweite Unterteilung unterscheiden lassen. Die feinste gemeinsame Vergröberung ist die triviale Partition, die nur aus einem Block, dem ganzen
R3 , besteht; denn hier werden je zwei Objekte miteinander identifiziert, wenn sie sich
bezüglich der einen oder der anderen Partition identifizieren lassen.
46
4.2 Partitionsverbände
Der im weiteren zentrale Begriff ist der einer Partition. Es gibt zwei unterschiedliche
Sichtweisen auf diesen Begriff – einen mengentheoretischen und einen algebraischen.
Wir beginnen mit ersterem.
Definition 4.2.1. Es sei W eine nichtleere Menge. Unter einer Partition verstehen wir
eine endliche Menge B1 , . . . , Bn von Teilmengen von W , so daß
(i) Bi ∩ Bj = ∅ für i 6= j,
(ii) B1 ∪ . . . ∪ Bn = W .
Die Elemente einer Partition werden Blöcke genannt.
M.a.W. ist eine Partition eine Unterteilung einer Menge in disjunkte Teilmengen.
Alternativ lassen sich Partitionen durch die Beziehung je zweier Elemente beschreiben,
demselben Block anzugehören.
Definition 4.2.2. Es sei a eine Partition aus der Menge W . Für v, w ∈ W definieren
wir
v ∼a w, falls v, w ∈ B für einen Block B von P .
Dann heißt ∼a die zu a gehörige Äquivalenzrelation.
Äquivalenzrelationen lassen sich wie folgt charakterisieren.
Lemma 4.2.3. Es sei W eine nichtleere Menge. Eine zweistellige Relation ∼ auf W
ist eine Äquivalenzrelation genau dann, wenn für alle u, v, w ∈ W Folgendes gilt:
(Ä1) v ∼ v (Reflexivität);
(Ä2) aus v ∼ w folgt w ∼ v (Symmetrie);
(Ä3) aus u ∼ v und v ∼ w folgt u ∼ w (Transitivität).
In diesem Fall ist ∼ die zu genau einer Partition a gehörige Äquivalenzrelation ∼a .
Die Blöcke von a sind die Mengen
hvi = {w ∈ W : w ∼ v}
(12)
für v ∈ W .
Beweis. a sei eine Partition von W und ∼ sei die zu a gehörige Äquivalenzrelation.
Definitionsgemäß gilt v ∼ w für v, w ∈ W genau dann, wenn v und w demselben
Block angehören. Diese Beziehung erfüllt offenbar (Ä1), (Ä2) und (Ä3).
Umgekehrt erfülle die Relation ∼ (Ä1), (Ä2) und (Ä3). Wir definieren für jedes v ∈ W
die Teilmenge hvi gemäß (12). Wir haben zu zeigen, daß die Mengen hvi, v ∈ W , eine
47
S
Partition von W bilden. Wegen (Ä1) ist v ∈ hvi, und es folgt v∈W hvi = W . Weiter
seien u, v ∈ W . Im Fall u ∼ v gilt w ∼ u, gdw w ∼ v, d.h. hui = hvi. Denn aus
w ∼ u folgt wegen (Ä3) w ∼ v; wegen (Ä2) folgt v ∼ u und damit umgekehrt aus
w ∼ v auch w ∼ u. Im Fall u 6∼ v gilt hingegen hui ∩ hvi = ∅; denn gäbe es ein
gemeinsames Element x ∈ hui∩hvi, hieße dies x ∼ u und x ∼ v, und die Konsequenz
wäre u ∼ v. Damit ist gezeigt, daß der Durchschnitt verschiedener Mengen hvi und
hwi leer ist.
Es sei a die so definierte Partition von W . Es gilt v ∼ w, gdw v ∈ hwi, und hieraus
folgt, daß v und w Element desselben Blocks sind. Gilt umgekehrt v, w ∈ hui für ein
u ∈ W , folgt v ∼ w. Also ist ∼ die zu a gehörige Äquivalenzrelation.
Es verbleibt zu bemerken, daß zu verschiedenen Partitionen verschiedene Äquivalenzrelationen gehören.
Definition 4.2.4. Es sei ∼ eine Äquivalenzrelation auf einer Menge W . Dann sagen
wir, daß die Partition, zu der ∼ gehört, die von ∼ induzierte Partition ist.
Mit einer Partition unterteilen wir Mengen; eine Unterteilung kann gröber oder feiner
gewählt werden. Wir befassen uns nun mit der Menge der Partitionen auf einer Grundmenge und führen in der naheliegenden Weise eine partielle Ordnung ein.
Definition 4.2.5. Es bestehe L aus Partitionen einer Menge W . Eine Partition a ∈ L
heiße feiner als eine weitere Partition b ∈ L, in Zeichen a ≤ b, falls jeder Block von a
in einem Block von b enthalten ist.
M.a.W. geht aus einer Partition b eine feinere a dadurch hervor, daß man die Blöcke
von b nochmals disjunkt aufteilt und die sich ergebenden Teilmengen zu Blöcken von
a erklärt.
Lemma 4.2.6. Es bestehe L aus Partitionen einer Menge W . Dann ist (L; ≤) ein
Poset.
Beweis. Es sei a, b, c ∈ L. Klarerweise gilt a ≤ a. Aus a ≤ b und b ≤ c folgt a ≤ c
wegen der Transitivität von ⊆.
Weiter bedeutet a ≤ b, daß jeder Block B ∈ a in einem Block B ′ ∈ b enthalten ist.
Gilt auch b ≤ a, folgt, daß auch B ′ in einem Block B ′′ ∈ a enthalten sein muß. Mit
jedem von B ′′ verschiedenen Block von a hat B ′ folglich einen leeren Durchschnitt,
und da B ′ ∩ B = B 6= ∅, muß B ′′ = B gelten. Also B = B ′ , und es folgt a = b.
Die ≤-Beziehung zwischen Partitionen nimmt ausgedrückt durch die zugehörigen Äquivalenzrelationen eine einfache Form an. Man beachte, daß eine zweistellige Relation
zwischen Mengen A und B eine Teilmenge des kartesischen Produktes A × B ist.
Lemma 4.2.7. Es bestehe L aus Partitionen einer Menge W . Für a, b ∈ L gilt a ≤ b
genau dann, wenn ∼a ⊆∼b .
48
Beweis. Es gelte a ≤ b. Es sei v, w ∈ W . Aus v ∼a w folgt, daß v und w demselben
Block von a, demzufolge auch demselben Block von b angehören, also v ∼b w gilt.
Es gelte ∼a ⊆∼b . Es sei A ein Block von a. Es sei v ∈ A, und es sei B der v enthaltende
Block von b. Für jedes w ∈ A gilt dann v ∼a w, also auch v ∼b w und damit w ∈ B.
Es folgt A ⊆ B.
M.a.W. ist die partielle Ordnung auf der Menge der Partitionen von W einfach eine
Teilmengenbeziehung auf W × W , wenn man mit jeder Partition deren zugehörige
Äquivalenzrelation identifiziert.
Satz 4.2.8. Es sei L die Menge aller Partitionen einer Menge W . Dann ist L ein
0, 1-Verband. Für a, b ∈ L besteht a ∧ b aus allen nichtleeren Mengen von der Form
A ∩ B für A ∈ a und B ∈ b. Das Nullelement 0̂ ist die aus allen einelementigen
Teilmengen von W bestehende Partition; das Einselement 1̂ ist die das einzige Element
W enthaltende Partition.
Zu gegebenem a, b ∈ L gilt weiter
v ∼a∧b w, gdw v ∼a w und v ∼b w,
v ∼a∨b w, gdw es u1 , . . . , uk gibt mit v ∼a u1 ∼b u2 ∼a . . . ∼a uk ∼b w
für v, w ∈ W . Zudem gilt
v ∼0̂ w, gdw v = w,
v ∼1̂ w stets
für v, w ∈ W .
Beweis. Es sei a, b ∈ L. Im Hinblick auf Lemma 4.2.7 müssen wir die größte in ∼a
und ∼b enthaltende Äquivalenzrelation auf W bestimmen. Wir behaupten, daß dies das
wie oben definierte ∼a∧b =∼a ∩ ∼b ist. In der Tat ist ∼a∧b eine Äquivalenzrelation;
die Bedingungen (Ä1) bis (Ä3) sind leicht verifizierbar. Klarerweise ist ∼a∧b die größte
untere Schranke von ∼a und ∼b . Also ist ∼a∧b das Infimum von ∼a und ∼b im Poset
aller Äquivalenzrelationen.
Zwei Elemente v, w ∈ W sind also im selben Block von a ∧ b, gdw v ∼a w und
v ∼b w, gdw v und w im selben Block von a und im selben Block von b liegen, gdw
v und w im Durchschnitt eines Blocks von a und eines Blocks von b liegen. Also sind
die Blöcke von a ∧ b genau die nichtleeren Durchschnitte je eines Blockes von a und b.
Im Hinblick auf Lemma 4.2.7 müssen wir weiter die kleinste ∼a und ∼b enthaltende
Äquivalenzrelation auf W bestimmen. Wir behaupten, daß dies das wie oben definierte
∼a∨b ist. In der Tat handelt es sich um eine Äquivalenzrelation; es ist nicht schwierig,
(Ä1) bis (Ä3) zu verifizieren. Andererseits sei ∼ eine Äquivalenzrelation mit ∼a ⊆∼
und ∼b ⊆∼. Aus (Ä3) folgt dann, daß auch ∼a∨b ⊆∼ gilt. Also ist ∼a∨b das Supremum
von ∼a und ∼b .
Die oben definierten Relationen ∼0̂ und ∼1̂ sind Äquivalenzrelationen auf W . Weiter
gilt ∼0̂ ⊆∼⊆∼1̂ für jede Äquivalenzrelation ∼ auf W , im ersten Fall wegen (Ä1). Also
ist 0̂ = {{v} : v ∈ W } und 1̂ = {W }.
49
Definition 4.2.9. Es sei W eine nichtleere Menge. Dann heiße der 0, 1-Verband aller Partitionen von W der Partitionsverband von W und sei mit (Part W ; ∩, ∨, 0̂, 1̂)
bezeichnet.
Den isomorphen 0, 1-Verband aller Äquivalenzrelationen auf W bezeichnen wir mit
(ÄR W ; ∩, ∨, 0̃, 1̃).
4.3 Darstellungstheorie
Interessanterweise ist das Beispiel eines Partitionsverbandes kein besonders spezielles:
Jeder Verband läßt sich in einen Partitionsverband einbetten. Dieses Resultat soll nun
hergeleitet werden. Wir teilen den Beweis in einzelne Lemmata auf.
Wir verwenden folgenden Hilfsbegriff. Es sei W eine nichtleere Menge und L ein
Verband mit 0; dann verstehen wir unter einer verbandswertigen Abstandsfunktion eine
Abbildung δ : W ×W → L, so daß für alle u, v, w ∈ W Folgendes gilt: (i) δ(v, v) = 0;
(ii) δ(v, w) = δ(w, v); (iii) δ(u, w) ≤ δ(u, v) ∨ δ(v, w).
Lemma 4.3.1. Es sei W eine nichtleere Menge, L ein Verband mit 0, und δ : W ×W →
L sei eine surjektive verbandswertige Abstandsfunktion. Für jedes a ∈ L ist dann
folgende binäre Relation auf W eine Äquivalenzrelation:
a
v∼w
falls δ(v, w) ≤ a
(13)
a
Es sei ϕ(a) die von ∼ induzierte Partition. Dann ist die Abbildung ϕ : L → Part W
eine Einbettung von Posets, die zudem Infima erhält.
Beweis. Die Eigenschaften (Ä1) bis (Ä3) einer Äquivalenzrelation werden durch (13)
a
offenbar erfüllt. Weiter sei a, b ∈ L mit a ≤ b; dann folgt für v, w ∈ W aus v ∼ w, daß
b
δ(v, w) ≤ b und damit v ∼ w gilt, d.h. ϕ(a) ≤ ϕ(b). Also ist ϕ ordnungserhaltend.
Wir haben aber mehr zu zeigen – den Erhalt von Infima unter ϕ. Es sei a, b ∈ L. Für
a∧b
v, w ∈ W gilt v ∼ w, gdw δ(v, w) ≤ a ∧ b, gdw δ(v, w) ≤ a und δ(v, w) ≤ b, gdw
a
b
v ∼ w und v ∼ w gilt. Also ist ϕ(a ∧ b) = ϕ(a) ∧ ϕ(b).
Es verbleibt, die Injektivität von ϕ nachzuprüfen. Es sei a, b ∈ L mit a 6≤ b. Wegen der
Surjektivität von δ können wir v, w ∈ W so wählen, daß δ(v, w) = a. Dann aber gilt
a
b
v ∼ w und nicht v ∼ w, d.h. ϕ(a) und ϕ(b) sind verschieden.
Eine L-wertige Abstandsfunktion gibt es für jeden Verband L. Damit ist klar, daß die
Einbettung von L in einen Partitionsverband kein Problem ist, wenn es nur darum geht,
die Infima zu erhalten.
Lemma 4.3.2. Es sei L ein Verband mit 0. Dann ist
(
a∨b
δ : L × L → L, (a, b) 7→
0
eine surjektive L-wertige Abstandsfunktion.
50
für a 6= b,
für a = b.
Beweis. Die Eigenschaften (i) bis (iii) einer verbandswertigen Abstandsfunktion sind
offenbar erfüllt.
Wir wenden uns nun der schwierigeren Aufgabe zu, einen Partitionsverband zu konstruieren, in den sich ein Verband einbetten läßt, d.h. auch unter Erhalt der Suprema.
Lemma 4.3.2 ist der Startpunkt. Als Grundbereich dient hier der Verband selbst; dieser
Grundbereich wird einer sukzessiven Vergrößerung unterworfen.
Lemma 4.3.3. Es sei W eine nichtleere Menge, L ein Verband mit 0, und δ : W ×W →
L sei eine surjektive L-wertige Abstandsfunktion. Dann gibt es eine Menge W + ⊇ W
und eine δ fortsetzende L-wertige Abstandsfunktion δ + auf W + , so daß Folgendes gilt:
(⋆) Es sei u, v ∈ W und a, b ∈ L mit δ(u, v) ≤ a ∨ b. Dann gibt es Elemente x, y, z ∈
W + mit
δ + (u, x) = a
δ + (x, y) = b
δ + (y, z) = a
δ + (z, v) = b.
Illustration von Lemma 4.3.3
Beweis. Wir führen den Beweis nur für den Fall, daß W abzählbar ist. Andernfalls
ist der Einsatz des sogenannten Auswahlaxioms notwendig, welches wir hier nicht
besprechen möchten.
51
Es seien
(ui , vi , ai , bi ) ∈ W × W × L × L,
i ∈ N,
sämtliche 4-Tupel mit der Eigenschaft δ(ui , vi ) ≤ ai ∨ bi . Es sei W0 = W und
δ0 = δ. Wir erweitern W0 um drei neue Elemente x0 , y0 , z0 und setzen W1 = W0 ∪
{x0 , y0 , z0 }. Ferner setzen wir δ0 zu einer Abstandsfunktion δ1 : W1 × W1 → L fort,
und zwar mit der Vorschrift
δ1 (x0 , y0 ) = b,
δ1 (y0 , z0 ) = a,
δ1 (x0 , z0 ) = a ∨ b,
sowie
δ1 (t, x0 ) = δ(t, u0 ) ∨ a,
δ1 (t, y0 ) = δ(t, u0 ) ∨ a ∨ b,
δ1 (t, z0 ) = δ(t, v0 ) ∨ b,
für jedes t ∈ W . Etwas mühsam, aber einfach ist es, aus δ(u0 , v0 ) ≤ a ∨ b abzuleiten,
daß δ1 wiederum eine L-wertige Abstandfunktion ist.
In der gleichen Weise konstruieren wir aus W1 und der L-wertigen Abstandsfunktion
δ1 auf W1 unter Verwendung des 4-Tupels (u1 , v1 , x1 , y1 ) eine Menge W2 und setzen
δ2 zur Abstandsfunktion δ2 auf W2 fort.
S
S
Am Ende setzen wir W + = i∈N Wi sowie δ + = i∈N δi . Damit ist der Beweis
abgeschlossen.
Wir kommen zum Hauptergebnis.
Satz 4.3.4. Es ein L ein Verband mit 0. Dann gibt es eine nichtleere Menge W , so daß
L in Part W einbettbar ist.
Beweis. Gemäß Lemma 4.3.2 wird durch δ 0 (a, b) = a ∨ b eine surjektive L-wertige
Abstandsfunktion auf der Grundmenge L definiert.
Es sei W 0 = L. Mit Bezug auf Lemma 4.3.3 setzen wir W 1 = (W 0 )+ und δ 1 =
(δ 0 )+ ; sodann W 2 = (W 1 )+ und δ 2 = (δ 1 )+ ; und so weiter.
S
S
Am Ende setzen wir W = i∈N W i und δ = i∈N δ i . Dann ist δ eine surjektive
L-wertige Abstandsfunktion auf W .
Nach Lemma 4.3.1 ist ϕ : L → Part W , definiert durch (13), eine ordnungstheoretische Einbettung. ϕ erhält sogar Infima, d.h. wir wissen, daß ϕ(a ∧ b) = ϕ(a) ∧ ϕ(b)
für a, b ∈ L gilt.
Wir behaupten, daß ϕ auch Suprema erhält, d.h. daß ϕ(a ∨ b) = ϕ(a) ∨ ϕ(b) gilt.
a∨b
Es sei v, w ∈ W mit v ∼ w. Es sei i hinreichend groß, so daß v, w ∈ W i . Aus
52
δ(v, w) ≤ a ∨ b folgt dann, daß es x, y, z ∈ Wi+1 ⊆ W gibt mit δ(u, x) = a,
a
b
a
b
δ(x, y) = b, δ(y, z) = a und δ(z, v) = b. Also ist u ∼ x, x ∼ y, y ∼ z und z ∼ v.
a∨b
a
b
Es ist ∼ = ∼ϕ(a)∨ϕ(b) sowie ∼ = ∼ϕ(a) und ∼ = ∼ϕ(b) . Nach Satz 4.2.8 folgt also,
daß ∼ϕ(a∨b) ⊆ ∼ϕ(a)∨ϕ(b) . Da klarerweise auch ∼ϕ(a) , ∼ϕ(b) ⊆ ∼ϕ(a∨b) gilt, folgt
sogar ∼ϕ(a∨b) ⊆ ∼ϕ(a)∨ϕ(b) , d.h. ϕ(a ∨ b) = ϕ(a) ∨ ϕ(b).
Indem wir Satz 4.3.4 mit 2.4.9 kombinieren, erhalten wir den folgenden Darstellungssatz für alle Verbände.
Satz 4.3.5. Es ein L. Dann gibt es eine nichtleere Menge W , so daß L in Part W
einbettbar ist.
Beweis. Hat L ein Nullelement, gilt die Behauptung nach Satz 4.3.4.
Andernfalls läßt sich L in einen Verband L0 mit 0 gemäß Satz 2.4.9 einbetten. L0
läßt sich wiederum gemäß Satz 4.3.4 in einen Partitionsverband einbetten, und die
Behauptung folgt auch in diesem Fall.
53
5 Modulare Verbände
5.1 Motivation
Zwar ist jeder Verband dem Unterverband eines Partitionsverbandes isomorph, aber es
ist klar, daß nicht in jedem Fall eine Darstellung interessiert, die Partitionen verwendet. Für die früher besprochenen distributiven Verbände etwa gibt es angemessenere
Darstellungen.
Es gibt aber eine Klasse von Verbänden, die als aus Partitionen hervorgehend betrachtet
werden können; diese sollen im Folgenden das Thema sein. Es sind dies diejenigen
Verbände, mit denen wir die Brücke von der abstrakten zur linearen Algebra schlagen
sowie zur projektiven Geometrie.
Die Bedeutung linearer Räume braucht wahrscheinlich nicht weiter hervorgehoben zu
werden. Insbesondere ist der reelle lineare Raum Standardstruktur der Mathematik; in
der Quantenphysik steht der komplexe lineare Raum im Mittelpunkt. Im ersteren Fall
ist der Grund klar; ausgehend von anschaulichen Formen werden wir zu reellen Zahlen
geführt und in einem weiteren Schritt zu Vektorräumen über diesen. Im letzteren Fall
ist der Grund nicht klar; warum gerade die merkwürdig definierten komplexen Zahlen
eine so prominente Rolle in der Quantenphysik spielen und vor allem komplexe Räume
mit innerem Produkt, ist bislang nicht überzeugend dargelegt worden.
Im gegebenen Zusammenhang werden wir zunächst auf lineare Räume allgemeineren
Charakters geführt, zu solchen über einem beliebigen Schiefkörper, wofür R und C
nur zwei einzelne Beispiele sind. Methoden zur Herausfilterung gerade der Standardschiefkörper ergeben sich durch eine modifizierte Herangehensweise.
Es geht um Verbände von Unterräumen; das nachfolgende ist das grundlegende Beispiel.
Definition 5.1.1. Es sei E ein linear Raum über einem Schiefkörper K. Wir setzen
U(V ) = {U ⊆ V : U ist Unterraum von E}
und ordnen U(V ) mittels der mengentheoretischen Inklusion ⊆ partiell.
Lemma 5.1.2. Es sei E ein linearer Raum. Dann ist U(E) verbandsgeordnet. Es seien U und V Unterräume von E. Dann ist deren mengentheoretischer Durchschnitt,
d.h. U ∩ V , das Infimum von U und V , und der von U ∪ V aufgespannte Unterraum
von E ist das Supremum von U und V . Zudem besitzt U(E) den Nullraum {0} als
Nullelement und den ganzen Raum E als Einselement.
Beweis. U ∩ V ist wie U und V unter den linearen Operationen abgeschlossen und
folglich ein Unterraum von E. Es ist U ∩ V die größte in U und V enthaltene Menge,
also auch der größte in U und V enthaltene Unterraum: das Infimum von U und V .
Enthält ein Unterraum W sowohl U als auch V , so auch alle Linearkombinationen von
Elementen von U und V , d.h. den von U und V aufgespannten Unterraum. Es folgt,
daß letzterer das Supremum von U und V ist.
54
Der Nullraum ist in allen Unterräumen enthalten, der ganze Raum enthält alle Unterräume. Also sind {0} und E Null- und Einselement.
Man erinnere sich, s. Beispiel 3.2.2, daß ein Unterraumverband, sofern der zugrundeliegende Vektorraum zumindest zweidimensional ist, nicht distributiv ist. Dafür aber
handelt es sich um einen Verband von Partitionen.
Lemma 5.1.3. Es sei E ein linearer Raum. Für jeden Unterraum U von E definieren
wir die Partition ϕ(U ) von E durch folgende Äquivalenzrelation:
U
x ∼ y,
falls x − y ∈ U ;
x, y ∈ E.
Dann ist das Bild P von ϕ in Part E ein Unterverband von Part E, und ϕ : U(E) → P
ist ein Isomorphismus von 0, 1-Verbänden.
U
Beweis. Es ist zunächst einmal offensichtlich, daß ∼ eine Äquivalenzrelation ist und
somit ϕ(U ) wohldefiniert ist.
U∩V
U
Wir zeigen, daß ∼ = ∼
∩
V
∼ gilt; daraus folgt ϕ(U ∧ V ) = ϕ(U ) ∩ ϕ(V ). Es sei
U∩V
x, y ∈ E. Es gilt x ∼ y, gdw x − y ∈ U ∩ V , gdw x − y ∈ U und x − y ∈ V , gdw
U
V
x ∼ y und x ∼ y gilt.
U∨V
U
V
Wir zeigen weiter ∼ = ∼ ∨ ∼; daraus folgt ϕ(U ∨ V ) = ϕ(U ) ∨ ϕ(V ). Es sei
U∨V
x, y ∈ E. Es gilt x ∼ y, gdw x − y ∈ U ∨ V , gdw x − y = λ1 u + λ2 v für u ∈ U ,
U
V
v ∈ v und λ1 , λ2 ∈ K gilt. Hieraus folgt, daß x ∼ x − λ1 u = y + λ2 v ∼ y und
U
V
damit x (∼ ∨ ∼) y gilt. Aus Letzterem folgt umgekehrt, daß es z1 , . . . , zk gibt mit
U
V
U∨V
V
U
x = z1 ∼ z2 ∼ z3 ∼ . . . ∼ zk = y; dann ist x − y ∈ U ∨ V , d.h. x ∼ .
Damit ist gezeigt, daß P eine unter Infimum und Supremum abgeschlossene Teilmenge von Part E, d.h. ein Unterverband von Part E ist und ϕ ein Isomorphismus von
Verbänden. Weiter wird offenbar {0} auf 0̂ und E auf 1̂ abgebildet.
5.2 Modulare und lineare Verbände
Jeder Verband L läßt sich in einen Partitionsverband Part W einbetten. Gemäß Satz
4.2.8 ist dabei die einem Infimum zweier Elemente a, b ∈ L zugeordnete Äquivalenza∧b
a
b
relation ∼ aus ∼ und ∼ konstruierbar: Es handelt sich einfach um den Durchschnitt.
Etwas unübersichtlicher geht es beim Supremum zu; es gilt
a∨b
v ∼ w, gdw es u0 , . . . , uk+1 gibt mit
a
#
b
v = u0 ∼ u1 ∼ u2 . . . uk ∼ uk+1 = w;
(14)
v, w ∈ W,
wobei # für a oder b steht, je nachdem ob k gerade oder ungerade ist.
Der Wert von k kann i.a. beliebig groß sein. Man kann sich jedoch fragen, ob man zu
gegebenem Verband eine Darstellung so wählen kann, daß der Wert von k von oben
beschränkt ist.
55
Definition 5.2.1. Es sei (L; ∧, ∨) ein Verband. Eine Einbettung ϕ : L → Part W
heiße eine Typ-n-Darstellung, falls für alle a, b ∈ L die zu ϕ(a ∨ b) gehörige Äquivalenzrelation gemäß (14) bestimmt ist, worin k ≤ n.
Ein Blick auf den Beweis des Darstellungssatzes 4.3.5 verrät:
Satz 5.2.2. Jeder Verband besitzt eine Typ-3-Darstellung.
Im vorliegenden Kapitel befassen wir uns mit denjenigen Verbänden, für die k = 2
genügt.
Definition 5.2.3. Ein Verband heiße modular, falls er eine Typ-2-Darstellung besitzt.
Wir befassen uns im weiteren mit Verbänden auf abstrakter Ebene, d.h. nicht im Hinblick auf eine spezielle Darstellung. Daher benötigen wir zunächst einmal ein Kriterium für Modularität, mit dem sich gut arbeiten läßt. Das im folgenden Satz enthaltende
Kriterium wird in der Literatur meist als Definition verwendet, ist aber völlig technischer Natur.
Satz 5.2.4. Ein Verband L ist modular genau dann, wenn Folgendes gilt:
(M) Es sei a, b, c ∈ L. Aus c ≤ a folgt a ∧ (b ∨ c) = (a ∧ b) ∨ c.
Den Beweis der einen Richtung von Satz 5.2.4 ist im folgenden Lemma enthalten.
Lemma 5.2.5. Der Verband L sei modular. Dann gilt (M) für alle a, b, c ∈ L.
Beweis. Es sei a, b, c ∈ L mit c ≤ a. Dann gilt (a ∧ b) ∨ c ≤ a ∧ (b ∨ c); wir haben
also zu zeigen, daß a ∧ (b ∨ c) ≤ (a ∧ b) ∨ c gilt.
Es sei ϕ : L → Part W eine Typ-2-Darstellung. Es seien v, w ∈ W mit v
a∧(b∨c)
∼
w.
(a∧b)∨c
Wir müssen zeigen, daß dann auch v ∼ w gilt. Denn dann ist klar, daß die Partition
ϕ(a ∧ (b ∨ c)) feiner ist als ϕ((a ∧ b) ∨ c), d.h. daß ϕ(a ∧ (b ∨ c)) ≤ ϕ((a ∧ b) ∨ c)
und damit auch a ∧ (b ∨ c) ≤ (a ∧ b) ∨ c gilt.
a∧(b∨c)
a
c∨b
Aus v ∼ w folgt zunächst v ∼ w und v ∼ w. Letzteres heißt gemäß Voraussetc
b
c
zung, daß es gewisse x, y ∈ W gibt mit v ∼ x ∼ y ∼ w. Wegen c ≤ a folgt weiter
a
a
a
a
a∧c
c
a∧c
c
x ∼ v ∼ w ∼ y, damit x ∼ y und weiter x ∼ y. Also v ∼ x ∼ y ∼ w, und es folgt
v
c∨(a∧b)
∼
w.
Als nächstes passen wir Lemma 4.3.3 an. Dann folgt die andere Richtung von Satz
5.2.4 genauso wie im Fall allgemeiner Verbände; s. den Beweis von Satz 4.3.4.
Lemma 5.2.6. Es sei W eine nichtleere Menge, L ein Verband mit 0, der (M) erfüllt,
und δ : W × W → L sei eine surjektive L-wertige Abstandsfunktion. Dann gibt es eine
Menge W + ⊇ W und eine δ fortsetzende L-wertige Abstandsfunktion δ + auf W + , so
daß Folgendes gilt:
56
(⋆) Es sei u, v ∈ W und a, b ∈ L mit δ(u, v) ≤ a ∨ b. Dann gibt es Elemente x, y ∈
W + mit
δ + (u, x) = a,
δ + (x, y) = b,
δ + (y, v) = a.
Illustration von Lemma 5.2.6
Beweis. Wiederum beschränken wir uns auf den Fall, daß W abzählbar ist.
Es seien
(ui , vi , ai , bi ) ∈ W × W × L × L,
i ∈ N,
sämtliche 4-Tupel mit der Eigenschaft δ(ui , vi ) ≤ ai ∨ bi . Es sei W0 = W und δ0 = δ.
Wir erweitern W0 um zwei neue Elemente x0 , y0 und setzen W1 = W0 ∪ {x0 , y0 }.
Ferner setzen wir δ0 zu einer Abstandsfunktion δ1 : W1 × W1 → L fort, und zwar mit
der Vorschrift
δ1 (x0 , y0 ) = (δ0 (u0 , v0 ) ∨ a) ∧ b,
δ1 (t, x0 ) = δ0 (t, u0 ) ∨ a,
δ1 (t, y0 ) = δ0 (t, v0 ) ∨ a
für jedes t ∈ W . Daß die Dreiecksungleichung auch für δ1 gilt, zeigen wir für das
57
Tripel t, x0 , y0 ; in den übrigen Fällen ist der Nachweis einfach oder ähnlich.
δ1 (t, y0 ) = δ0 (t, v0 ) ∨ a
≤ δ0 (t, u0 ) ∨ δ0 (u0 , v0 ) ∨ a
≤ δ0 (t, u0 ) ∨ δ0 (u0 , v0 ) ∨ a
≤ δ0 (t, u0 ) ∨ ((δ0 (u0 , v0 ) ∨ a) ∧ (b ∨ a))
≤ δ0 (t, u0 ) ∨ (δ0 (u0 , v0 ) ∨ a) ∧ b) ∨ a
≤ δ0 (t, u0 ) ∨ a ∨ ((δ0 (u0 , v0 ) ∨ a) ∧ b)
≤ δ0 (t, x0 ) ∨ δ0 (x0 , y0 )
worin wir δ0 (t, x0 ) ≤ a ∨ b sowie die Modularität verwendet haben.
In der gleichen Weise konstruieren wir aus W1 und der L-wertigen Abstandsfunktion
δ1 auf W1 unter Verwendung des 4-Tupels (u1 , v1 , x1 , y1 ) eine Menge W2 und setzen
δ2 zur Abstandsfunktion δ2 auf W2 fort.
S
S
Am Ende setzen wir W + = i∈N Wi sowie δ + = i∈N δi . Damit ist der Beweis
abgeschlossen.
Ein weiteres häufig verwendetes Charakteristikum von Modularität ist das folgende.
Lemma 5.2.7. Es sei (L; ∧, ∨) ein modularer Verband und a, b ∈ L. Dann ist
ib : [a, a ∨ b] → [a ∧ b, b], x 7→ x ∧ b
ein Isomorphismus. Die Umkehrabbildung ist der Isomorphismus
sa : [a ∧ b, b] → [a, a ∨ b], x 7→ x ∨ a.
Beweis. Zunächst einmal folgt aus a ≤ x ≤ a ∨ b, daß a ∧ b ≤ ib (x) ≤ b, und
aus a ∧ b ≤ x ≤ b, daß a ≤ sa (x) ≤ a ∨ b gilt. Weiter ist klar, daß ib und sa
ordnungserhaltende Abbildungen sind.
Wir zeigen, daß sa ◦ ib die Identität auf [a, a ∨ b] und ib ◦ sa die Identität auf [a ∧ b, b]
ist. Dann folgt, daß ib bijektiv ist und sa die Umkehrabbildung von ib ist. Als bijektive
ordnungserhaltende Abbildung ist ib gemäß Lemma 2.3.22(ii) ein Verbandshomomorphismus. Entsprechendes gilt für ib .
Für x ∈ [a, a ∨ b] ist wegen a ≤ x
sa (ib (x)) = (x ∧ b) ∨ a
= x ∧ (b ∨ a)
= x;
und ähnlich erschließen wir ib (sa (x)) = x für x ∈ [a ∧ b, b].
Die für uns eigentlich interessantesten Verbände sind die, für die in Definition 5.2.1
sogar k = 1 genügt. Denn hierunter fällt das Beispiel linearer Unterräume.
58
Definition 5.2.8. Ein Verband heiße linear, falls er eine Typ-1-Darstellung besitzt.
Lemma 5.2.9. Jeder lineare Verband ist modular.
Beweis. Ein Typ-k-Verband ist gemäß Definition auch ein Typ-k ′-Verband für 1 ≤
k ′ < k.
Wir wiederholen das zentrale Beispiel.
Beispiel 5.2.10. Es sei E ein linearer Raum über dem Schiefkörper K. Die Menge
U(E) aller Unterräume von E ist gemäß Lemma 5.1.2 ein Verband.
Wir hatten zudem gesehen, daß sich U(E) als ein Verband von Partitionen begreifen
läßt. Jedem U ordnen wir die Partition ϕ(U ) zu, die zur Äquivalenzrelation
U
x ∼ y falls x − y ∈ U
für x, y ∈ E
U∨V
gehört. Für x, y ∈ E gilt x ∼ y, gdw x − y ∈ U ∨ V , gdw x − y = λu + µv für
U
V
u ∈ U , v ∈ v und λ, µ ∈ K. Das aber heißt x ∼ x − λu ∼ x − λu − µv = y. Also ist
ϕ eine Typ-1-Darstellung.
Wir werden im weiteren allerdings nicht von der Tatsache Gebrauch machen, daß Unterraumverbände vom Typ 1 und nicht bloß vom Typ 2 sind. Lineare Verbände lassen
sich nämlich nicht in so einfacher Weise charakterisieren wie gemäß Satz 5.2.4 modulare.
5.3 Atomistische Verbände
Wir stellen im weiteren Eigenschaften von Verbänden zusammen, die insbesondere auf
Unterraumverbände zutreffen.
Definition 5.3.1. Ein Verband L mit 0 heiße atomistisch [engl. atomistic], falls jedes
von 0 verschiedene a ∈ L das Supremum aller Atome e mit e ≤ a ist.
Lemma 5.3.2. Es sei E ein linear Raum. Die Atome des Verbandes (U(E); ∩, ∨, {0}, E)
sind genau die eindimensionalen Unterräume, d.h. die Unterräume der Form [v] für ein
v ∈ E mit v 6= 0. Weiter ist U(E) atomistisch.
Beweis. Es sei v ∈ E mit v 6= 0. Dann folgt für einen Unterraum U aus {0} ⊂ U ⊆
[v], daß w ∈ U für ein w 6= 0 gilt und weiter w = λv für ein λ ∈ K. Also [v] = U ,
und [v] ist ein Atom. Enthält andererseits ein Unterraum U zwei linear unabhängige
Elemente v und w, folgt {0} ⊂ [v] ⊂ U , d.h. U ist kein Atom. Also ist jedes Atom von
U(E) von der Form [v] für ein v 6= 0.
Weiter sei U ein von {0} verschiedener Unterraum. Dann ist [v] ⊆ [U ] für jedes v ∈ U
mit v 6= 0. Also ist U die Vereinigung und folglich das Supremum aller Atome [v] ⊆
U.
59
Definition 5.3.3. Es sei L ein Verband mit 0. Wir sagen, daß L die Bedeckungseigenschaft [engl. covering property] erfüllt, falls für jedes a ∈ L und jedes Atom e mit
a∧e=0
a <· a ∨ e
gilt.
Lemma 5.3.4. Es sei E ein linear Raum über K. Dann erfüllt (U(E); ∩, ∨, {0}, E)
die Bedeckungseigenschaft.
Beweis. Es sei U ein Unterraum von E und A ein Atom von U(E) mit U ∩ A = {0}.
Gemäß Lemma 5.3.2 ist A = [v] für ein v ∈ E, v 6= 0. Es ist U ∨ A = U ∨ [v] =
{λu + µv : u ∈ U, λ, µ ∈ K}. Wegen v ∈
/ U ist U ⊂ U ∨ v.
Weiter sei V ein Unterraum mit U ⊂ V ⊆ U ∨ [v]. Angenommen, v 6= V ; dann folgt
V ⊆ U , ein Widerspruch. Also V = U ∨ [v], d.h. U <· U ∨ [v].
Lemma 5.3.5. Ein modularer Verband erfüllt die Bedeckungseigenschaft.
Beweis. L sei ein modularer Verband. Es sei a ∈ L und e ein Atom mit a ∧ e = 0.
Gemäß Lemma 5.2.7 ist
ϕ : [a, a ∨ e] → [0, e], x 7→ x ∧ e
ein Isomorphismus und insbesondere bijektiv. Also besteht [a, a ∨ e] aus ebensovielen
Elementen wie [0, e]: aus zweien.
Definition 5.3.6. Es sei L ein Verband mit 0. Wir sagen, daß L die Austauscheigenschaft [engl. exchange property] erfüllt, falls für jedes a ∈ L und Atome e, f ∈ L aus
a ∧ e = 0 und e ≤ a ∨ f folgt, daß f ≤ a ∨ e gilt.
Man beachte, daß für Elemente a, e, f eines Verbandes e ≤ a ∨ f und f ≤ a ∨ e
zusammengenommen sogar a ∨ e = a ∨ f bedeutet.
Lemma 5.3.7. Es sei E ein linear Raum über K. Dann erfüllt (U(E); ∩, ∨, {0}, E)
die Austauscheigenschaft.
Beweis. Es sei U ein Unterraum von E und u, v ∈ E, u, v 6= 0. Dann heißt U ∩[u] = 0,
daß u ∈
/ U ; und [u] ⊆ U ∨ [v] heißt, daß u = λw + µv für w ∈ U , λ, µ ∈ K.
Da dann weiter µ 6= 0 gelten muß, ist v eine Linearkombination von u und w; also
[v] ⊆ U ∨ [u].
Lemma 5.3.8. Erfüllt ein Verband mit 0 die Bedeckungseigenschaft, so auch die Austauscheigenschaft.
Beweis. Es sei L ein die Bedeckungseigenschaft erfüllender Verband mit 0. Weiter
sei a ∈ L und seien e, f Atome von L mit a ∧ e = 0 und e ≤ a ∨ f . Dann gilt
a < a ∨ e ≤ a ∨ f . Weiter gilt a ∧ f = 0, da andernfalls a ∨ f = a gälte. Aus der
Bedeckungseigenschaft folgt a ∨ e = a ∨ f und insbesondere f ≤ a ∨ e.
60
Lemma 5.3.9. Ein modularer Verband erfüllt die Austauscheigenschaft.
Beweis. Die folgt aus den Lemmata 5.3.5 und 5.3.8.
Definition 5.3.10. Es sei L ein atomistischer Verband mit 0. Dann heißen Atome
e1 , . . . , en ∈ L unabhängig [engl. independent], falls
(e1 ∨ . . . ∨ ei−1 ∨ ei+1 ∨ . . . en ) ∧ ei = 0
für alle i = 1, . . . n gilt.
Lemma 5.3.11. Es seien e1 , . . . , en von 0 verschiedene Elemente eines Vektorraums
E. Dann bildet [e1 ], . . . , [en ] eine unabhängige Teilmenge im Verband U(E) genau
dann, wenn e1 , . . . , en linear unabhängige Vektoren in E sind.
Beweis. In beiden Fällen bedeutet Nichtgelten, daß einer der Vektoren eine Linearkombination der übrigen ist.
Satz 5.3.12. Es sei L ein atomistischer modularer 0, 1-Verband. Weiter seien e1 , . . . , em ,
m ≥ 1, und f1 , . . . , fn , n ≥ 1, zwei Mengen unabhängiger Atome mit
e1 ∨ . . . ∨ em ≤ f1 ∨ . . . ∨ fn .
(15)
Dann folgt m ≤ n.
Gilt insbesondere in (15) sogar Gleichheit, folgt m = n.
Beweis. O.B.d.A. nehmen wir an, daß (15) nach Streichung eines der Disjunkte f1 , . . . , fn
nicht gilt. Weiter nehmen wir an, daß n < m gilt.
Wir wählen ein i1 ∈ {1, . . . , m}, für welches ei1 ∧ (f2 ∨ . . . ∨ fn ) = 0 gilt. Ein solches
i1 muß es geben; denn andernfalls wäre ei ≤ f2 ∨. . .∨fn für alle i, also e1 ∨. . .∨em ≤
f2 ∨ . . . ∨ fn , im Widerspruch zur Annahme. Da zudem ei1 ≤ f1 ∨ (f2 ∨ . . . ∨ fn ) gilt,
folgt wegen der Austauscheigenschaft f1 ∨ . . . ∨ fn = ei1 ∨ f2 ∨ . . . ∨ fn .
Dasselbe Argument wenden wir nun auf f2 ∨ ei1 ∨ f3 ∨ . . . ∨ fn = e1 ∨ . . . ∨ em an. Wir
bestimmen also ein i2 ∈ {1, . . . , n}, für welches ei2 ∧(ei1 ∨f3 ∨. . .∨fn ) = 0 gilt. Man
beachte, daß i2 6= i1 sein muß. Wir erschließen f1 ∨ . . . ∨ fn = ei1 ∨ ei2 ∨ f3 ∨ . . . ∨ fn .
n-malige Anwendung des Argumentes bringt schließlich f1 ∨ . . . ∨ fn = ei1 ∨ ei2 ∨
. . . ∨ ein . Dann aber sind die e1 , . . . , em nicht unabhängig.
Lemma 5.3.13. Es sei L ein atomistischer modularer 0, 1-Verband. Ist a ∈ L das
Supremum von n unabhängigen Atomen, 1 ≤ n < ω, ist n die Höhe von a.
Beweis. Es sei a = e1 ∨ . . . ∨ em , worin e1 , . . . , em unabhängige Atome sind. Aus der
Unabhängigkeit der ei und der Bedeckungseigenschaft von L folgt, daß dann
0 <· e1 <· e1 ∨ e2 <· . . . <· e1 ∨ . . . ∨ em = a
gilt. Insbesondere gibt es eine Kette der Länge n in [0, a], d.h. a ist mindestens von der
Höhe n.
61
Wir müssen zeigen, daß es keine längere Kette in [0, a] gibt; dann ist klar, daß a genau
von der Höhe n ist. Es sei 0 < b1 < b2 < . . . < bm = a eine weitere Kette in [0, a].
Es sei dann f1 ≤ b1 ein Atom. Es sei f2 ≤ b2 ein Atom mit f2 ∧ b1 = 0; ein solches
muß es geben, da andernfalls alle f2 ≤ b2 unterhalb b1 lägen, im Widerspruch zur
Atomizität von L. In dieser Weise konstruieren wir eine Folge unabhängiger Atome
f1 , . . . , fm mit f1 ∨ . . . ∨ fm ≤ bm = a. Aus Satz 5.3.12 folgt m ≤ n.
Lemma 5.3.14. Es sei L ein atomistischer modularer 0, 1-Verband, und a, b ∈ L seien
endlich. Dann gilt
h(a) + h(b) = h(a ∧ b) + h(a ∨ b).
(16)
Beweis. Mit a und b ist offensichtlich auch a ∨ b endlich.
Wir betrachten zunächst das Intervall [a, a ∨ b]. Die Höhe von a in L plus die Höhe von
a ∨ b in [a, a ∨ b] ist die Höhe von [a ∨ b] in L. Also ist h(a ∨ b) − h(a) die Höhe von
a ∨ b im Intervall [a, a ∨ b], d.h. die Länge des Verbandes [a, a ∨ b]. Ähnlich erschließen
wir, daß die Länge des Verbandes [a ∧ b, b] gleich h(b) − h(a ∧ b) ist. Beide sind wegen
Lemma 5.2.7 aber isomorph; die Behauptung folgt.
Lemma 5.3.15. Es sei E ein linearer Raum und U ein n-dimensionaler Unterraum
von E, 1 ≤ n < ω. Dann ist die Höhe von U im Verband U(E) gleich n.
Beweis. Dies folgt aus Lemma 5.3.11 und Lemma 5.3.13.
Wir fahren fort mit der Charakterisierung von Unterraumverbänden.
Lemma 5.3.16. Es sei E ein linearer Raum über K. Dann ist U(E) ein vollständiger
Verband.
T
Beweis. Es seien Uι , ι ∈ I, Unterräume von E. Dann ist ι Uι unter Linearkombinationen abgeschlossen, folglich wieder ein Unterraum und damit das Infimum der Uι .
Weiter ist
{λ1 u1 +. . .+λn un : u1 ∈ Uι1 , . . . , un ∈ Uιn für ι1 , . . . , ιn ∈ I sowie λ1 , . . . , λn ∈ K}
der kleinste alle Uι enthaltende Unterraum und folglich deren Supremum.
Definition 5.3.17. Ein Verband L heiße kompakt atomistisch, falls L vollständig und
atomistisch ist und es für jedes Atom e ∈ L und jede Menge fι , ι ∈ I, von Atomen mit
_
e≤
fι
ι
eine endliche Teilmenge ι1 , . . . , ιk ∈ I gibt, so daß
e ≤ fι1 ∨ . . . ∨ fιk .
Lemma 5.3.18. Es sei E ein linearer Raum über K. Dann ist U(E) kompakt atomistisch.
62
W
Beweis. Es seien u, vι , ι ∈ I, Vektoren in E mit [u] ⊆ ι [vι ]. Das heißt, daß u in
dem von den vι aufgespannten Vektorraum liegt; m.a.W. ist u eine Linearkombination
gewisser vι1 , . . . , vιk , ι1 , . . . , ιk ∈ I. Also [u] ⊆ [vι1 ] ∨ . . . ∨ [vιk ].
Schließlich stellen wir die Komplementierung betreffenden Eigenschaften von Unterraumverbänden fest.
Lemma 5.3.19. Es sei E ein linearer Raum. Dann ist U(E) relativ komplementiert
und insbesondere komplementiert.
Beweis. Es seien U und V Unterräume mit U ⊂ V . Weiter sei U ⊆ W ⊆ V . Es sei
˙ 2 ∨B
˙ 3 ∨B
˙ 4 eine Basis von E, so daß B1 eine Basis von U , B1 ∨ B2
nun B = B1 ∨B
eine solche von W und schließlich B1 ∨ B2 ∨ B3 eine Basis von V ist. W ′ sei der von
B1 ∨ B3 aufgespannte Unterraum. Dann ist jedes u ∈ W ∩ W ′ Linearkombination von
Vektoren aus B1 ∨ B2 sowie solchen aus B1 ∨ B3 , also nur solchen aus B1 ; es folgt
W ∩ W ′ = U . Offensichtlich ist W ∨ W ′ = V . Also ist W ′ relatives Komplement von
W in [U, V ].
Wir beweisen nun, daß man kompakt atomistische Verbände in Bestandteile zerlegen“
”
kann.
Lemma 5.3.20. Es sei L ein atomistischer modularer Verband. Für Atome p und q
von L setzen wir p ∼ q, falls entweder p = q gilt oder es andernfalls ein von p und q
verschiedenes Atom r ≤ p ∨ q gibt. Dann ist ∼ eine Äquivalenzrelation.
Beweis. Es seien p, q, r Atome von L. Gemäß der Definition von ∼ gilt p ∼ p und ist
p ∼ q mit q ∼ p gleichwertig. Also ist ∼ reflexiv und symmetrisch.
Wir nehmen weiter an, daß p ∼ q und q ∼ r gilt, um hieraus p ∼ r abzuleiten;
dann wird auch die Transitivität gezeigt sein. Sind zwei der Atome gleich, folgt p ∼ r
unmittelbar. Wir nehmen an, daß p, q, r paarweise verschieden sind. Ist r ≤ p ∨ q, folgt
wegen der Austauscheigenschaft q ≤ p ∨ r, d.h. auch dann gilt p ∼ r. Wir nehmen
weiter an, daß r 6≤ p ∨ q gilt, daß also r, p, q unabhängig sind.
Gemäß Definition von ∼ gibt es dann ein von p und q verschiedenes s ≤ p ∨ q und ein
von q und r verschiedenes t ≤ q ∨r. Wir setzen u = (s∨t)∧(p∨r); dann ist u ≤ p∨r.
Gemäß Lemma 5.3.14 gilt h(u) = h(s∨t)+h(p∨r)−h(s∨t∨p∨r) = 2+2−3 = 1,
da s ∨ t ∨ p ∨ r = p ∨ q ∨ r ist. Also ist u ein Atom, und p ∼ r.
Lemma 5.3.21. Es sei L ein relativ komplementierter, kompakt atomistischer modularer Verband. Es seien a, b ∈ L, und es sei e ein Atom von L mit e ≤ a ∨ b. Dann gibt
es Atome ea ≤ a und eb ≤ b mit e ≤ ea ∨ eb .
Beweis. Da L kompakt atomistisch ist, können wir annehmen, daß a und b endlich
sind. Weiter ist der Fall e ≤ a oder e ≤ b trivial. Wir nehmen im weiteren an, daß
a ∧ e = b ∧ e = 0. Einfach ist auch der Fall a ∧ b > 0; dann wählen wir ein Atom
ea = eb ≤ a ∧ b. Wir nehmen im weiteren an, daß a ∧ b = 0.
63
Wir setzen ea = (b ∨ e) ∧ a ≤ a. Wir rechnen h(a ∨ b) = h(a) + h(b) − h(a ∧ b) =
h(a) + h(b) sowie h(b ∨ e) = h(b) + 1 und erhalten h(ea ) = h(b ∨ e) + h(a) − h(a ∨
b ∨ e) = h(b ∨ e) + h(a) − h(a ∨ b) = 1, also ist ea ein Atom. Wir setzen ebenso
eb = (a ∨ e) ∧ b und schließen in analoger Weise, daß eb ≤ b ein Atom ist. Wegen der
Modularität folgt
ea ∨ eb = [(e ∨ b) ∧ a)] ∨ eb
= (e ∨ b) ∧ (a ∨ eb )
= (e ∨ b) ∧ (a ∨ [(e ∨ a) ∧ b])
= (e ∨ b) ∧ (a ∨ b) ∧ (e ∨ a)
= (e ∨ b) ∧ (e ∨ a)
≥ e.
Satz 5.3.22. Es sei L ein relativ komplementierter, kompakt atomistischer modularer
Verband. Dann ist L direktes Produkt unzerlegbarer Verbände.
Beweis. Es seien Eι , ι ∈ I, die Äquivalenzklassen
bezüglich der Relation ∼ aus LemW
ma 5.3.20. Für jedes ι ∈ I sei zι = Eι .
Wir behaupten, daß für jedes a ∈ L und ι ∈ L
(a ∨ b) ∧ zι = (a ∧ zι ) ∨ (b ∧ zι )
gilt. Es sei e ≤ (a∨b)∧zι ein Atom; wir müssen zeigen, daß dann e ≤ (a∧zι )∨(b∧zι )
gilt. Ist e ≤ a oder e ≤ b, folgt dies unmittelbar. Es gelte andererseits weder e ≤ a
noch e ≤ b. Wegen Lemma 5.3.21 gibt es Atome ea ≤ a und eb ≤ b mit e ≤ ea ∨ eb .
Dann sind e, ea , eb paarweise verschieden, weshalb all diese drei Atome in derselben
Äquivalenzklasse liegen; wegen e ≤ zι ist folglich ea , eb ≤ zι . Es folgt e ≤ ea ∨ eb ≤
(a ∧ zι ) ∨ (b ∧ zι ).
Wir folgern, daß
ϕ : L → Πι∈I [0, zι ], a 7→ (a ∧ zι )ι∈I
eine Verbandshomomorphismus ist.
Ist a b, gibt es ein Atom e ≤ a, e b. Dann ist e ≤ zι für ein ι ∈ I, und e ≤ a ∧ zι ,
aber e b ∧ zι . Also ist a ∧ zι 6= b ∧ zι , d.h. ϕ ist injektiv. Schließlich folgt aus der
Vollständigkeit von L, daß ϕ surjektiv ist.
Es sei ι ∈ I. Wäre [0, zι ] zerlegbar, gäbe es x, y ≤ zι mit x ∧ y = 0 und x ∨ y = zι ,
so daß jedes a von der Form a = ax ∨ ay für ax ≤ x und ay ≤ y wäre. Für beliebige
Atome e ≤ x und f ≤ y gibt es, da e ∼ f gilt, jedoch ein drittes Atom g ≤ e ∨ f , so
daß g kann nicht von der besagten Form sein kann.
5.4 Projektive Geometrien
Lemma 5.4.1. Es sei E ein linearer Raum über einem Schiefkörper K. A(E) sei
die Menge aller eindimensionalen Unterräume von E. Wir ordnen je zwei Elementen
64
P, Q ∈ A(E) den von diesen aufgespannten Unterraum P Q = [P, Q] zu. Dann erfüllt
das Paar (A(E), ··) folgende Eigenschaften:
(i) Es seien P, Q ∈ A(E). Es gilt P P = {P }, und im Fall P 6= Q ist P Q mindestens dreielementig.
(ii) Es seien P, Q ∈ A(E) verschieden. Dann gibt es genau einen zweidimensionalen Unterraum, der P und Q enthält.
(ii) Es seien P, Q, R ∈ A(E) paarweise verschieden und nicht alle drei in einem
zweidimensionalen Unterraum von E enthalten. Weiter seien S ∈ P Q und T ∈
QR verschieden. Dann ist P R ∩ ST nichtleer.
Beweis. (i) Es sei P = [p] und Q = [q], p, q ∈ E. Klarerweise ist P Q = [p] im
Fall P = Q. Andernfalls ist p 6= q, sind p und q also linear unabhängig. Damit ist
der Vektor p + q weder in P noch in Q; es sind [p], [q], [p + q] drei verschiedene in
P Q = [p, q] enthaltene eindimensionale Unterräume.
(ii) Es sei P = [p] und Q = [q], p, q ∈ E. P und Q sind in einem zweidimensionalen
Unterraum genau dann enthalten, wenn dieser p und q und damit [p, q] enthält. [p, q]
ist aber der einzige zweidimensionale Unterraum, der [p, q] enthält; denn jeder größere
wäre mindestens dreidimensional.
(iii) Es sei P = [p], Q = [q] und R = [r], p, q, r ∈ E. Gemäß Voraussetzung
sind p, q, r linear unabhängig. Weiter sei S = [s] und T = [t], s, t ∈ E. Dann ist
s = λ1 p + λ2 q und t = λ3 q + λ4 r für λ1 , . . . , λ4 ∈ K. Aus λ3 s − λ2 t ∈ [p, r] folgt,
daß [p, r] ∩ [s, t] nicht leern ist.
Definition 5.4.2. Es sei A eine nichtleere Menge, und es sei ·· eine Abbildung, die
je zwei Elementen p, q ∈ A eine Teilmenge pq von A zuordnet. Wir bezeichnen ein
p ∈ A als Punkt [engl. point] und für verschiedene Punkte p und q die Menge pq als
die durch p und q verlaufende Gerade [engl. line]. Weiter gelte Folgendes:
(PR1) Es sei p, q ∈ A. Dann enthält pq die beiden Punkte p und q. Ferner enthält pq
noch mindestens einen weiteren Punkt genau dann, wenn p und q verschieden
sind.
(PR2) Je zwei verschiedene Punkte liegen auf genau einer Geraden.
(PR3) Es seien p, q, r ∈ A, so daß es keine Gerade gibt, die durch all die drei Punkte
verläuft. Weiter seien s ∈ pq und t ∈ qr verschiedene Punkte. Dann haben pr
und st eine nichtleere Schnittmenge.
Dann nennen wir (A, ··) einen projektiven Raum [engl. projective space].
Eine nichtleere Teilmenge U von A, für die mit p, q ∈ U auch pq ⊆ U gilt, heiße
Unterraum [engl. subspace] von A. Für zwei Unterräume U, V setzen wir
[
U +V =
{pq : p ∈ U, q ∈ V }.
65
Illustration des Axioms (PR3)
(s. Lemma 5.4.1 und Definition 5.4.2)
Der Einfachheit halber nehmen wir im weiteren auf einen projektiven Raum als auf
dessen Punktemenge Bezug; die Zuordnung ·· versteht sich jeweils.
Lemma 5.4.3. Es sei A ein projektiver Raum, und U, V seien zwei seiner Unterräume.
Dann ist auch U + V ein Unterraum.
Beweis. Wir beweisen zunächst Folgendes:
(⋆) Es seien U, V, W Unterräume. Dann gilt U + (V + W ) = (U + V ) + W .
Es sei p ∈ U + (V + W ). Dann gibt es u ∈ U , v ∈ V und w ∈ W , so daß p ∈ ur,
worin r ∈ vw.
Fall 1: u = v. dann ist p ∈ vr und r ∈ vw. Sind r, v, w nicht paarweise verschieden,
folgt p ∈ V + W ⊆ (U + V ) + W . Es seien r, v, w paarweise verschieden. Dann ist
p ∈ vr = vw ⊆ V + W ⊆ (U + V ) + W .
Fall 2: u 6= v und r ∈ uv. Ist r = u oder r = v, folgt p ∈ U + V ⊆ (U + V ) + W .
Andernfalls sind u, v, r paarweise verschiedene Punkte, die auf einer Gerade liegen.
Da r ∈ vw, liegt w dann ebenfalls auf dieser Gerade. Also p ∈ uw oder p ∈ vw, je
nachdem ob w von u oder von v verschieden ist. Es folgt p ∈ U + W bzw. p ∈ V + W
und in jedem Fall p ∈ (U + V ) + W .
Fall 3: u 6= v und r ∈
/ uv. Es ist p ∈ ur und w ∈ vr. Zudem gilt v 6= w, da sonst
r = v wäre. Ist nun w = p, so p ∈ W ⊆ (U + V ) + W . Andernfalls besagt Bedingung
(PR3), daß es ein s ∈ pw ∩ uv gibt. Da v 6= w, muß s 6= w sein. Also folgt p ∈ sw mit
s ∈ U + V und w ∈ W , d.h. p ∈ (U + V ) + W .
Damit ist U + (V + W ) ⊆ (U + V ) + W bewiesen; aus Symmetriegründen folgt auch
der umgekehrte Einschluß. Damit ist der Beweis von (⋆) abgeschlossen.
Aus (⋆) leiten wir nunmehr die Behauptung des Lemmas ab. Es sei p, q ∈ U + V . Dann
ist
pq ⊆ (U + V ) + (U + V ) = ((U + V ) + U ) + V
= (U + (U + V )) + V = ((U + U ) + V ) + V
= (U + V ) + V = U + (V + V ) = U + V.
66
Definition 5.4.4. Es sei (A, ··) ein projektiver Raum. Dann sei L(A) der durch mengentheoretische Inklusion geordnete Poset aller Unterräume von (A, ··).
Lemma 5.4.5. Es sei (A, ··) ein projektiver
T Raum. Dann ist L(A) ein vollständiger
Verband. Für Unterräume Uι , ι ∈ I, ist ι∈I Uι deren Infimum; weiter gilt
_
ι∈I
Uι =
[
{Uι1 + . . . + Uιk : ι1 , . . . ιk ∈ I, k ≥ 1}.
(17)
Beweis. Der Durchschnitt einer beliebigen
Menge von Unterräumen Uι , ι ∈ I, ist
T
wieder ein Unterraum; daher ist ι∈I Uι das Infimum der Uι . Es folgt bereits daß
L(A) ein vollständiger Verband ist.
Das Supremum der Uι muß die rechte Seite von (17) enthalten. Andererseits folgt
aus Lemma 5.4.3, daß die rechte Seite von (17) unter ·· abgeschlossen und damit ein
Unterraum ist.
Lemma 5.4.6. Es sei (A, ··) ein projektiver Raum. Dann ist L(A) ein modularer Verband.
Beweis. Es seien U, V, W Unterräume, W ⊆ U , und es sei r ∈ U ∧(V ∨W ); wir haben
zu zeigen, daß dann r ∈ (U ∧V )∨W folgt. Gemäß Lemma 5.4.5 gilt r ∈ U ∩(V +W ),
und wir haben zu zeigen, daß r ∈ (U ∩ V ) + W . Wir wissen r ∈ U sowie r ∈ vw
für gewisse v ∈ V und w ∈ W ⊆ U . Im Fall r = w ist r ∈ W ⊆ (U ∩ V ) + W .
Andernfalls ist v 6= w und v ∈ vw = rw ⊆ U , also v ∈ U ∩ V . Wegen r ∈ vw folgt
also r ∈ (U ∩ V ) + W .
Für den Typ von Verbänden, die als Unteraumverbände projektiver Räume auftauchen,
gibt es eine spezielle Bezeichnung.
Definition 5.4.7. Ein kompakt atomistischer, komplementierter, unzerlegbarer modularer Verband heiße geomodular.
Satz 5.4.8. Es sei (A, ··) ein projektiver Raum. Dann ist L(A) ein geomodularer Verband.
Beweis. Gemäß Lemma 5.4.6 ist L(A) ein modularer Verband.
Weiter ist gemäß Lemma 5.4.5 L(A) ein vollständiger Verband. Die eindimensionalen
Unterräume sind genau die Atome. Jeder Unterraum ist die mengentheoretische Vereinigung seiner eindimensionalen Unterräume und somit deren Supremum. Es folgt, daß
L(A) atomistisch ist. Aus Lemma 5.4.5 folgt, daß L(A) kompakt atomistisch ist.
Angenommen sei schließlich, daß L(A) zerlegbar ist. Dann gibt gemäß Satz 5.3.22
und dessen Beweis zwei Unterräume U und V mit U ∩ V = ∅ und U ∪ V = A. Jede
Gerade uv mit u ∈ U und v ∈ V enthält jedoch ein von u und v verschiedenes drittes
Element w; und w liegt weder in U noch in V .
Es gilt hiervon auch eine Umkehrung.
67
Definition 5.4.9. Es sei (L; ∧, ∨, 0, 1) ein geomodularer Verband. Es sei A(L) die
Menge aller Atome von L. Für p, q ∈ A(L) sei
pq = {r ∈ A(L) : r ≤ p ∨ q}.
(18)
Satz 5.4.10. Es sei (L; ∧, ∨, 0, 1) ein geomodularer Verband. Dann ist A(L) zusammen mit der Zuordnung (18) ein projektiver Raum.
Dessen Unterräume sind genau die Mengen der Form {p ∈ A : p ≤ a}. Die Abbildung
ϕ : L → L(A(L)), a 7→ {p ∈ A : p ≤ a}
ist ein Isomorphismus.
Beweis. (PR1) Auf L ist Satz 5.3.22 anwendbar. Daher folgt aus der Unzerlegbarkeit,
daß für je zwei verschiedene Atome p und q von L ein drittes, von p und q verschiedenes, liegt. Also ist pq mindestens dreielementig. Zudem ist pp = p.
(PR2) L ist modular, erfüllt nach Lemma 5.3.9 also die Austauscheigenschaft. Sind
p, q, r paarweise verschiedene Atome, sind die Aussagen p ≤ q ∨ r und q ≤ p ∨ r und
r ≤ p ∨ q daher paarweise äquivalent. Liegen also zwei verschiedene Punkte p, q auf
einer Gerade, ist diese gleich p ∨ q. Haben also zwei Geraden zwei Punkte gemeinsam,
sind sie gleich.
(PR3) Es seien p, q, r Atome, die nicht auf einer Gerade liegen. Dann sind p, q, r unabhängig, und es folgt h(p ∨ q ∨ r) = 3. Weiter seien s ≤ p ∨ q und t ≤ q ∨ r
verschiedene Atome, womit h(s ∨ t ∨ p ∨ r) ≤ 3. Also h((s ∨ t) ∧ (p ∨ r)) =
h(s ∨ t) + h(p ∨ r) − h(s ∨ t ∨ p ∨ r) ≥ 2 + 2 − 3 = 1. Also ist st ∩ pr nicht
leer.
Es folgt der erste Teil des Satzes: A(L) ist ein projektiver Raum.
Für jedes a ∈ L ist ϕ(a) offenbar ein Unterraum von A(L). Weiter ist ϕ ist ordnungserhaltend. Da L atomistisch ist, folgt zudem, daß ϕ injektiv ist.
W
Weiter sei U ein Unterraum von A(L), und es sei a = U . Wir wollen zeigen, daß
U = ϕ(a) gilt; denn dann folgt, ϕ auch surjektiv und mithin ein Verbandsisomorphismus ist. Klarerweise ist U ⊆ ϕ(a). W
Umgekehrt sei p ∈ ϕ(a), also p ≤ a. Da L
kompakt atomistisch ist, folgt aus p ≤ U , daß es Atome q1 , . . . , qk ∈ U gibt mit
p ≤ q1 ∨ . . . ∨ qk . Aus Lemma 5.3.21 folgt p ∈ U und damit ϕ(a) ⊆ U .
5.5 Darstellungstheorie
Geomodulare Verbände führen auf direktem Wege zur linearen Algebra; sie sind zu
Unterraumverbänden isomorph. Diesen Zusammenhang wollen wir zum Abschluß der
Vorlesung anführen.
Satz 5.5.1. Es sei (L; ∧, ∨, 0, 1) ein geomodularer Verband der Länge n ≥ 4. Dann
gibt es genau einen Schiefkörper K, so daß L isomorph zu (U(E); ∩, ∨, {0}, E) ist,
worin E ein n-dimensionaler linearer Raum über K ist.
68
Den Beweis von Satz 5.5.1, der von erheblichem Umfang ist, werden wir nicht geben.
Wir werden jedoch, um wenigstens einen Eindruck von der Komplexität des Konstruktionsprozesses zu vermitteln, die Einführung von Koordinaten eines zweidimensionalen projektiven Raumes grob darstellen.
Unter einer projektiven Ebene verstehen wir einen projektiven Raum, dessen zugehöriger Verband die Länge 3 hat. Ein Beispiel ist die reelle projektive Ebene RP2 erfolgen;
der zugehörige Verband ist U(R3 ), d.h. der Verband der Unterräume des dreidimensionalen reellen Raumes. Anschaulich besteht RP2 aus den Geraden durch den Ursprung
des R3 . Alternativ läßt sich RP2 als die Einheitssphäre im R3 verbildlichen, auf der je
zwei gegenüberliegende Punkte miteinander identifiziert sind.
Einem Punkt der projektiven Ebene RP2 entspricht je ein eindimensionaler Unterraum
x
[ y ], x, y, z ∈ R,
z
worin die drei Koordinaten x, y, z nicht alle drei gleich 0 sein dürfen und zudem nur
bis auf einen Faktor eindeutig bestimmt sind. Die Koordinatendarstellung läßt sich
eindeutig machen, indem gefordert wird, daß die letzte von 0 verschiedene Koordinate
1 sei. Dann entsprechen den Punkten folgende Koordinatentripel:
x
x
1
y , x, y ∈ R,
1 , x ∈ R sowie
0 .
1
0
0
Angenommen, es läßt sich jedem Punkt einer projektiven Ebene ein Koordinatentripel
zuordnen; wie erhalten wir dann aus der Struktur der projektiven Ebene die additive und
multiplikative Struktur der Koordinatenmenge? Die Idee ist die folgende, mit Bezug
auf den RP2 ; es sei a, b, λ ∈ R:
a
a
0
0
1
1
[ b ] ∈ [ µ ] ∨ [ 1 ], gdw für ein λ ∈ R [ b ] ∈ [ µ + λ 1 ],
1
1
0
0
1
1
a
λ b
] = [ λ+µ ],
gdw für ein λ ∈ R [
1
1
gdw a = λ und b = λ + µ.
0
M.a.W. enthält die von [ b ], b ∈ R, und [
1
a der Form [ a+b ], a ∈ R.
1
1
Ähnlich enthält die von [ b ], b ∈ R, und [
0
a der Form [ a·b ], a ∈ R.
1
1
1 ]
0
0
0 ]
1
aufgespannte Gerade die Punkte von
aufgespannte Gerade die Punkte von
Wir skizzieren nun, wie die Einführung von Koordinaten im allgemeinen funktioniert.
Es sei F eine projektive Ebene. R sei eine Menge von Symbolen, vom Umfang her eines weniger als Punkte auf einer Gerade liegen; darunter seien insbesondere die Symbole 0 und 1. Dann ordnen wir wie folgt jedem Punkt von F ein Tripel aus R zu:
• Wir wählen vier Punkte X, Y, Z, I von F , so daß je drei nicht auf einer Geraden
liegen.
Wir setzen X = (1, 0, 0), Y = (0, 1, 0), Z = (0, 0, 1) und I = (1, 1, 1).
69
• Wir ordnen auch den übrigen Punkten auf ZI\XY Koordinatentripel von der
Form (a, a, 1) zu, wobei für verschiedene Punkte verschiedene Symbole zu verwenden sind. Für den verbleibenden Punkt setzen wir ZI ∩ XY = (1, 1, 0).
• Für a, b ∈ R sei X(b, b, 1) ∩ Y (a, a, 1) = (a, b, 1).
Für a ∈ R sei schließlich Z(a, 1, 1) ∩ XY = (a, 1, 0).
Sodann definieren wir die Operationen + und · auf R. Wir setzen a + b = c, wenn
(a, c, 1) ∈ (0, b, 1)(1, 1, 0) gilt. Wir setzen a · b = c, wenn (c, a, 1) ∈ (b, 1, 0)Z.
Z=(0,0,1)
(a,0,1)
)
a,1
(a,
(a,b,1)
(0,b,1)
(b,b,1)
(b
,1
,1
)
I=(1,1,1)
X=(1,0,0)
(1,1,0)
(b,1,0)
Addition von b
Multiplikation mit b
Y=(0,1,0)
Illustration der Koordinatisierung einer projektiven Ebene
Die so spezifierte Algebra (R; +, ·, 0, 1) ist ein sogenannter Ternärring. Mittels des
Ternärrings R läßt sich die projektive Ebene F darstellen.
Jeder Schiefkörper ist ein Ternärring; die Umkehrung gilt nicht. Unter gewissen Bedingungen ist der oben konstruierte Ternärring ein Schiefkörper; der Beweis ist umfangreich.
70
Literatur
[Art]
[Bae]
R. Artzy, Linear Geometry“, Addison-Wesley, Reading 1974.
”
R. Baer, Linear Algebra and Projective Geometry“, Academic Press, New
”
York 1952.
[BeRo] A. Beutelspacher, U. Rosenbaum, Projektive Geometrie“ (2. Aufl.), Vieweg,
”
Wiesbaden 2004.
[Bir]
G. Birkhoff, Lattice Theory“, American Mathematical Society Coll. Publ. 25,
”
1948.
[CrDi] P. Crawley, R.P. Dilworth, Algebraic Theory of Lattices“, Prentice-Hall,
”
Englewood Cliffs N.J., 1973.
[Gra]
G. Grätzer, General Lattice Theory“ (2. Aufl.), Birkhäuser, Basel 2003.
”
[MaMa] F. Maeda, S. Maeda, Theory of Symmetric Lattices“, Springer-Verlag, Ber”
lin 1970.
[Sik]
R. Sikorski, Boolean Algebras“, Springer-Verlag, Berlin 1964.
”
71