34. Elektromagnetische Wellen

Elektrizitätslehre – Elektromagnetische Wellen
34.
Elektromagnetische Wellen
34.1.
Die MAXWELLschen Gleichungen
−
Die MAXWELLschen Gleichungen sind die Differentialgleichungen, die die gesamte Elektrodynamik bestimmen. Wir kennen sie praktisch schon, sie sollen
hier nur noch einmal zusammengestellt werden.
−
Zuvor noch eine Verallgemeinerung: der Verschiebungsstrom
!
Wir laden einen Kondensator auf ⇒ um den Strom herum baut sich ein Magnetfeld auf.
Was ist jedoch im Kondensator-Innenraum?
Zwischen den Platten
existiert ein veränderliches elektrisches
r&
Feld D , um das herum sich ebenfalls ein
Magnetfeld bildet.
!
Der Verschiebungsstrom
& ⋅A
I v = ε 0 ⋅ E& ⋅ A + P& ⋅ A = ε ⋅ ε 0 ⋅ E& ⋅ A = D
(1)
ist ebenso felderzeugend wie ein „richtiger Strom“ (d.h. fließende Ladungen)!
Kommentar:
Mit Materie im Kondensator kann man sich IV sogar als Bewegung der Polarisar&
tionsladungen vorstellen. Aber eigentlich ist es die Tatsache, dass ein D ein ror&
r
r
tierendes H -Feld erzeugt, so wie B ein rotierendes E -Feld schafft.
Die folgende Gleichung muss also erweitert werden!
r
H
∫ ⋅ dr = I ≡
⇒
r
∫ j ⋅ dA
(29 -10‘)
Fläche
r
r
d r
H
⋅
dr
=
j
⋅
dA
+
∫
∫
∫ D ⋅ dA
dt
Kurve um A
A
A
â
Iges durch A
(2)
â
Verschiebungsstrom
Dies ist die Integralform des Durchflutungsgesetzes („1. MAXWELLsche Gleichung“).
106
Elektrizitätslehre – Elektromagnetische Wellen
Wie in <30.1.> bilden wir die differentielle Form von Gl. (2)
r r& r
rot H = D + j
−
(3)
Es waren
Φm =
r
B
∫ ⋅ dA
(29 - 13)
Fläche
und
r
&m =
−Φ
∫ E ⋅ dr
(30 - 4)
geschl. Kurve
Durch Gleichsetzen erhält man
⇒
r
d r
E
⋅
dr
=
−
B ⋅ dA
∫
dt A∫
K
(4)
Gl. (4) ist das Induktionsgesetz („2. MAXWELLsche Gleichung“).
Seine differentielle Form kennen wir schon
r
r&
rot E = − B
−
(30 - 8)
Die sogenannte 3. MAXWELLsche Gleichung in integraler und differentieller
Form lautet
r
D
∫ ⋅ dA = Q ges
(25 -10‘)≡
(5)
r
div D = ρ
(25 -20‘)≡
(6)
A
−
1
Die analogen Ausdrücke für das Magnetfeld lauten bekanntlich
r
B
∫ ⋅ dA = 0
(29 - 11)
r
div B = 0
(29 - 12)
A
Diese beiden Gleichungen drücken die Tatsache aus, dass keine magnetischen
Ladungen existieren!
−
1
Die Gleichungen (2), (3), (4), (30 - 8), (5), (6), (29 - 11) und (29 - 12) sind die
MAXWELLschen Gleichungen.
r
r
In den Gl. (25 - 10) und (25 - 20) stand lediglich E = ε −01 ⋅ D !
107
Elektrizitätslehre – Elektromagnetische Wellen
34.2.
−
Elektromagnetische Wellen: Einführung
In <30.2.> haben wir bei der Herleitung der LENZschen Regel gesehen:
... dass ein veränderlicher Magnetfluss nach dem Induktionsgesetz (Gl. (30 - 4)) in einem
Leiterring einen Strom hervorruft, der ein Magnetfeld besitzt,
das seiner Entstehungsursache
entgegengesetzt ist.
−
(X)
r& r
Nun zeigen uns die MAXWELLschen Gleichungen, dass D ≠ 0 (ein zeitlich veränderliches elektrisches Feld) völlig äquivalent zu einem „richtigen“ (Leitungs-)
Strom ist (Gl. (2) bzw. (3)), d.h., die oben dargestellte Feldanordnung (X) bildet
sich auch ohne Leiter!
Kommentar:
·
·
r
r& r
Entscheidend ist, dass D ≠ 0 ist, denn dies ist äquivalent zu j . Wenn zufälr&
r& r
lig B = const. ist, ist D = 0 und es gibt kein sekundäres Magnetfeld.1
r
Wenn aber z.B. B( t ) einer sin- oder cos-Funktion folgt, sind alle aufeinanderfolgenden Ableitungen wieder sin-/cos-Funktionen und daher nie konstant.
u
⇒ wie beispielhaft in der Abbildung dargestellt, ergibt sich in unendlicher Folge:
r&
veränderliches magnetisches Feld B ⇒ darum rotierendes elektrisches
Feld ⇒ darum rotierendes magnetisches Feld, usw.
Dies ist eine elektromagnetische Welle
34.3.
−
Ebene Elektromagnetische Wellen
Auch für die elektromagnetischen Wellen gilt das in <16.> Gesagte, also:
·
·
Eine Welle ist die räumliche Ausbreitung eines Schwingungszustandes.
Die allgemeine (eindimensionale) mathematische Form lautet
y( x, t ) = f ( x − v Ph ⋅ t ) = f (∗)
1
(16 - 1)
Diese Aussage gilt so nur für den Fall ohne Leiterring, mit Leiterring existiert wegen des fließenden
Stromes natürlich ein sekundäres Magnetfeld!
108
Elektrizitätslehre – Elektromagnetische Wellen
·
Also sind x und t über ∗ verkoppelt. Es ist keine Periodizität nötig (z.B.
Stoßwelle)!
Besonders wichtig sind harmonische Wellen (sin- oder cos-Funktionen)
Eine ebene harmonische elektromagnetische Welle hat also folgende Gestalt
r r
E = E 0 ⋅ sin(ωt − k ⋅ x )
k ... Wellenzahl
mit
k=
(7)
2π
λ
Zur Erinnerung: Es gilt auch
v Ph =
−
ω
k
(16 - 4)
Wir überlegen uns jetzt an Hand der MAXWELLschen Gleichungen die Grundeigenschaften der elektromagnetische Wellen:
1.) Elektromagnetische Wellen sind transversal, d.h. die Felder sind senkrecht zur
Ausbreitungsrichtung orientiert.
!
r
S ... Vektor in Ausbreitungsrichtung
r
( H ist hier die zweckmäßigere Beschreibung für das Magnetfeld)
Dass es eine Longitudinalwelle ist, lässt sich ausschließen. Eine solche
Welle (unten) hätte Quellen und Senken:
r
r
Da es aber Quellen/Senken für E bzw. D (= Ladungen) im leeren Raum
r
r
nicht gibt und für B bzw. H überhaupt nicht gibt, kann es sich nicht um
Longitudinalwellen handeln!
109
Elektrizitätslehre – Elektromagnetische Wellen
2.) Elektrisches und magnetisches Feld stehen senkrecht aufeinander.
!
Wir betrachten eine Leiterschleife (Fläche A, Randkurve K) im Feld einer
elektromagnetischen Welle, die um die Ausbreitungsrichtung der elektromagnetischen Welle drehbar gelagert ist.
Aus der Kenntr r
nis, dass E , D
r
immer ⊥ zu S
stehen müssen,
folgt
sofort,
dass dies auch
r& r&
für E , D gelten
muss.
In der gezeichneten Darstellung ist
r&
D
∫ ⋅ dA = max .
A
Lt. Gl. (2) muss damit auch
r
H
∫ ⋅ dr = max .
K
r
r
r r
sein, d.h. H bzw. B liegen in der Leiterschleifenebene, also senkrecht zu E , D !
3.) Elektrisches und magnetisches Feld sind in Phase, d.h. Maxima, Minima
und Nulldurchgänge befinden sich an gleicher Stelle.
!
Wir betrachten wieder die bereits verwendete Leiterschleife, deren Lage
jetzt jedoch entlang der Ausbreitungsrichtung der elektromagnetischen
Welle variiert wird.
110
Elektrizitätslehre – Elektromagnetische Wellen
In der gezeichneten Stellung fängt die Leiterschleife
r&
∫ D ⋅ dA = max .
A
r&
ein, da D am Punkt (3) maximal wird!
Lt. Gl. (2) muss damit auch wieder
r
H
∫ ⋅ dr = max .
K
r
r
sein, d.h. H muss bei (1) und (2) ein Maximum haben, so wie D !
4.) Ausbreitungsgeschwindigkeit: Wir betrachten Gl. (2) für die Leiterschleife
in der unter 3.) dargestellten Position zum Zeitpunkt t = 0:
r
r&
H
⋅
dr
=
D
∫
∫ ⋅ dA
K
r&
D ⋅ dA = D ⋅ dA = D ⋅ b ⋅ dx
A
3
λ
4
= b ⋅ ∫ ε ⋅ ε 0 ⋅ E& ⋅ dx
⇒
1
λ
4
Aus Gl. (7) wird
E& = ω ⋅ E 0 ⋅ cos(ωt − k ⋅ x )
Dies nun für eine Momentaufnahme bei t = 0 betrachtet ergibt
E& = ω ⋅ E 0 ⋅ cos(− k ⋅ x ) = ω ⋅ E 0 ⋅ cos(k ⋅ x )
1
Mit diesem Ergebnis nimmt das Durchflutungsgesetz folgende Form an
3
⇒
λ
4
r
∫ H ⋅ dr = b ⋅ ε ⋅ ε 0 ⋅ ω ⋅ E 0 ⋅ ∫ cos kx ⋅ dx 2bH 0
1
λ
4
K
Nach Lösen der Integrale ergibt sich
2bH 0 = b ⋅ ε ⋅ ε 0 ⋅ ω ⋅
1
1
3
1
⋅ E 0 ⋅ (sin π − sin π)
k
2
2
â
= -2
Hierbei wurde ausgenutzt, dass die cos-Funktion eine gerade Funktion ist.
111
Elektrizitätslehre – Elektromagnetische Wellen
Wir lassen das Minuszeichen weg, da es uns nur um die Beträge geht und
verwenden die Beziehung
1 v
=
k ω
so dass sich unser Ergebnis schreiben lässt als
⇒
H0 = ε ⋅ ε0 ⋅ v ⋅ E0
(8)
Analog folgt aus Gl. (4) (2. MAXWELLschen Gleichung)
E0 = µ ⋅ µ0 ⋅ v ⋅ Η 0
(9)
Gleichsetzen und umstellen von Gl. (8) und (9) liefert
⇒
v=
1
(10)
εε 0 µµ 0
für die Phasengeschwindigkeit der elektromagnetische Welle in einem Medium (ε, µ).
Im Vakuum (ε = µ = 1) folgt aus Gl. (10)
v Vakuum ≡ c =
34.4.
−
ε 0µ 0
(29 - 9)
Für reine elektrische oder magnetische Felder war die Energiedichte
w elektr =
1
1
⋅ E ⋅ D = ⋅ ε ⋅ ε0 ⋅ E 2
2
2
(28 - 16)
w magn =
1
1
⋅ B ⋅ H = ⋅ µ ⋅ µ0 ⋅ H2
2
2
(30 - 23)
Im elektromagnetischen Wellenfeld ist
w = w elektr. + w magn. =
1
1
Energiedichte und Energieströmung
bzw.
−
1
1
⋅ (ε ⋅ ε 0 ⋅ E 2 + µ ⋅ µ 0 ⋅ H 2 )
2
(11)
Damit hätten wir jetzt Gl. (29 - 9) „richtig“ hergeleitet!
112
Elektrizitätslehre – Elektromagnetische Wellen
−
Umstellung von Gl. (8) und (9) nach v und Gleichsetzung liefert
H0 1
E
1
⋅
=v= 0 ⋅
E 0 εε 0
H 0 µµ 0
⇒
E 02 ⋅ ε ⋅ ε 0 = µ ⋅ µ 0 ⋅ H 02
(12)
Wenn Gl. (12) für die Amplituden E0, H0 gilt, gilt sie auch für E(t) lt. Gl. (7) sowie für H(t).
⇒ Zur Energiedichte lt. Gl. (11) tragen magnetisches und elektrisches Feld je
zur Hälfte bei:
⇒
−
w=
1
⋅ (ε ⋅ ε 0 ⋅ E 2 + µ ⋅ µ 0 ⋅ H 2 ) = ε ⋅ ε 0 ⋅ E 2 = µ ⋅ µ 0 ⋅ H 2
2
!
(11‘)
Zur Beschreibung der Energieströmung verwendet man die Energiestromdichte S
S = w⋅v
å æ
Energiedichte Ausbreitungsgeschwindigkeit
Wenn wir hier Gl. (10) und (11‘) einsetzen, folgt
S = ε ⋅ ε0 ⋅ E 2 ⋅
1
εε 0 µµ 0
=
εε 0
⋅ E2
µµ 0
(13)
Aus Gl. (12) folgt nach Umstellung
H0 =
εε 0
⋅ E0
µµ 0
deshalb kann Gl. (13) auch geschrieben werden als
S = w ⋅v = E⋅H
−
(14)
In Vektorschreibweise (die Energiestromdichte hat Betrag und Richtung!) ausgedrückt:
r r r
S = E×H
(15)
r
S wird auch als Poynting-Vektor bezeichnet.
−
Strahlungsdruck: Die Energiedichte w hat die Dimension
[w] =
[Energie] [Kraft ] ⋅ [ Weg] [Kraft ]
=
=
= [Druck ]
[Volumen]
[Volumen]
[Fläche]
Dies kann tatsächlich als Druck interpretiert werden.
113
Elektrizitätslehre – Elektromagnetische Wellen
Kommentar:
Der Strahlungsdruck ist eine allgemeine Eigenschaft für jede Welle, da jede
Welle Impuls transportiert (Schallwellen, etc.)
·
Natürlich spielt die Richtung eine Rolle, deshalb wird er besser als Energier
stromdichte/Ausbreitungsgeschwindigkeit ausgedrückt, z.B. S ⋅ v −1 . Dies
r
hat auch den Betrag w, aber die Druckrichtung ist über S mit enthalten.
·
Der Strahlungsdruck ist im Allgemeinen gering, aber er verhindert den
Kollaps im Innern von Sternen (durch Gravitation) oder beeinflusst die
Bahn kleinerer Satelliten.
·
34.5.
−
u
!
!
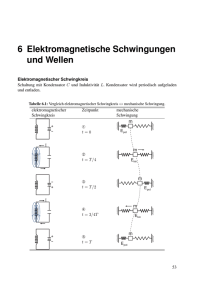
Der Dipoloszillator
Bei einem elektrischen Schwingkreis (vgl. <33.1.>) ist
·
das Magnetfeld auf das Spuleninnere beschränkt,
·
das elektrische Feld auf den Plattenzwischenraum beschränkt:
!
r&
r
Für die Ausbildung eines rotierenden E -Feldes um B bzw. eines rotierenden
r&
r
H -Feldes um D „ist kein Platz“!
−
Bei weniger idealen Bauteilen geht dies aber!
Außer den OHMschen
Verlusten treten nun auch
Abstrahlungsverluste auf:
−
Weitere Vereinfachung:
⇒
114
Elektrizitätslehre – Elektromagnetische Wellen
−
Der gestreckte Draht kann durch Einkopplung elektromagnetischer Schwingungen mit ω = ω0 (Resonanzfrequenz) zu einem elektrischen Oszillator (elektrischer Dipol mit zeitlich veränderlichem Dipolmoment) gemacht werden.
−
Wir schauen uns nun das Schwingen eines solchen Dipols an.
t
Prinzipdarstellung
Spannungsverteilung
Stromverteilung
0
1
⋅T
4
1
⋅T
2
3
⋅T
4
Für t = T stellt sich der gleiche Zustand ein wie bei t = 0.
Es herrscht also ein ständiges Pendeln zwischen den Extremen:
r
a) maximale Aufladung der Enden: p = max . ; ∆U = max.; I = 0, und
r
b) keine Aufladung der Stabenden: p = ∆U = 0 ; I = max.
Kommentar: zur Strom-Verteilung
Der Strom I ist an den Enden immer Null, da ja (in völliger Analogie zur stehenden mechanische Welle) „dort Schluss ist“.
−
u
Eigenfrequenz:
Man erkennt aus den Abbildungen (wieder analog den mechanischen Wellen), dass gilt
l=
λ
2
115
Elektrizitätslehre – Elektromagnetische Wellen
Damit folgt aus der bekannten Beziehung
c = ν⋅λ
dass
c = ν⋅2⋅l,
und nach Umstellung ergibt sich
⇒
ν=
c
2l
(16)
Beispiel: Wir betrachten einen Dipolstab mit 2 × l = 3 m. Mit Gl. (16) erhält man
n
3 ⋅ 10 8 m ⋅ s −1
1
ν=
= 10 8 = 100 MHz
3m
s
−
Untersuchen wir nun die Feldabstrahlung
·
Wenn ein Dipol durch Ladungstrennung neu entsteht, entsteht auch sein
Dipolfeld. Es kann nicht sofort überall sein, sondern breitet sich vom Dipol
mit Lichtgeschwindigkeit aus.
⇒ bei
bei
bei
bei
1
⋅ T + dt
4
1
⋅T
2
3
⋅ T − dt
4
3
⋅ T + dt
4
!
r
beginnt die E -Feld-Ausbreitung
ist die gerade losgeschickte Feldstärke maximal
hört die Ausbreitung auf
r
beginnt die E -Feld-Ausbreitung in der Gegenrichtung
Dieser Vorgang lässt sich schwierig vorstellen, denn es herrschen
r
a) ein zeitlich veränderliches Dipolmoment p( t ) und
b) eine endliche Ausbreitungsgeschwindigkeit.
·
r
Analog fluktuiert das H -Feld mit der Stromstärke:
⇒ bei
bei
bei
bei
0
+ dt
1
⋅T
4
1
⋅ T − dt
2
1
⋅ T + dt
2
r
beginnt die H -Feld-Ausbreitung
ist die gerade losgeschickte Feldstärke maximal
hört die Abstrahlung auf
r
beginnt die H -Feld-Ausbreitung in der Gegenrichtung
116
Elektrizitätslehre – Elektromagnetische Wellen
·
Veranschaulichung:
Wir betrachten die Feldstärke in der Mittelebene bei t =
−
1
⋅ T + ∆t
2
Richtcharakteristik eines Dipols:
Die maximale Emission erfolgt
senkrecht zum Dipol und ist rotationssymmetrisch.
−
!
Ein magnetischer Dipol ist
ein mit HF beschickter
Stromring.
({1}, S. 344}
117
Elektrizitätslehre – Elektromagnetische Wellen
·
·
r
r
Die Feldlinien von H entsprechen denen des E -Feldes des elektrischen Dipols und umgekehrt. Auch die Richtcharakteristik, etc. sind völlig gleich.
Es besteht eine begriffliche Schwierigkeit: Die Fluktuation des Kreisstromes
r
r
und damit von H ist verständlich. Für das elektrische Feld E gibt es aber im
Fall des magnetischen Dipols eine solche gegenständliche Feldquelle nicht.
⇒ „Es sind eben eigentlich immer nur die MAXWELLschen Gleichungen,
mit den ‚rotierenden Feldern‘“!
34.6.
Wellengleichung
−
Elektromagnetische Wellen sind spezielle Lösungen der MAXWELLschen Gleichungen.
Wir wollen die völlige „innere Einheit aller Arten von Wellen deutlich machen.
−
Die D’ALEMBERTsche Wellengleichung (eindimensional) war lt. <16.2.>
∂2y
1 ∂2y
=
⋅
∂x 2 v 2Ph ∂t 2
!
(16 - 6‘)
Damals war y die Auslenkung bei einer mechanischen Welle. Die elektromagnetischen Wellen müssen natürlich einer völlig analogen Gleichung gehorchen.
−
Wir schreiben das Induktionsgesetz in differentieller Form unter Verwendung
des Nabla-Operators
∇≡
∂ r ∂ r ∂ r
i+
j+ k
∂z
∂x
∂y
r r
r
wobei i , j und k die Einheitsvektoren in x-, y- und z-Richtung sind.
⇒
−
r
r
r
∂B
rot E ≡ ∇ × E = −
∂t
(30 - 8)
Anwendung von „ ∇ × “ auf beiden Seiten ergibt
r
∇ × (∇ × E )
r
∂B
= −∇ ×
∂t
Mathematische Umformung liefert
r
r
r
r
∂
∂
∇ ⋅ (∇ ⋅ E ) − ∇ 2 E = − (∇ × B) = − rot B
∂t
∂t
â
r ρ
≡ div E =
= 0 (im freien Raum!)
ε0
(17)
118
Elektrizitätslehre – Elektromagnetische Wellen
−
Bekanntlich ist
r r& r
rot H = D + j
(3)
Wenn wir die drei darin enthaltenen Größen ersetzen mit
r
1 r
H =
⋅B,
µ0
r&
r&
D = ε 0 ⋅ E und
r r
j = 0 (letzteres, weil der Raum leer ist),
dann folgt aus Gl. (3)
⇒
r&
r
rot B = µ 0 ⋅ ε 0 ⋅ E
(18)
Gl. (18) nach der Zeit t abgeleitet ergibt
r
∂2 r
∂
rot B = µ 0 ⋅ ε 0 ⋅ 2 E
∂t
∂t
å
1
≡ 2 (wegen Gl. (29 - 9)
c
−
(19)
Mit Gl. (19) können wir Gl. (17) schreiben als
r 1 ∂2 r
∇2E = 2 ⋅ 2 E
c ∂t
(20a)
bzw. in Komponentenschreibweise
r
∂2 r ∂2 r ∂2 r
1 ∂2 r
∇ E = 2 E+ 2 E+ 2 E = 2 ⋅ 2 E
∂x
∂y
∂z
c ∂t
2
(20b)
r
Dies ist die D’ALEMBERTsche Wellengleichung für das elektrische Feld E , völlig analog zu Gl. (16 - 6).
−
r
Genauso kann man für das magnetische Feld B herleiten1
r
1 ∂2 r
∇2B = 2 ⋅ 2 B
c ∂t
1
(21)
Wir wollen uns hier jedoch die Komponentendarstellung schenken.
119
Elektrizitätslehre – Elektromagnetische Wellen
Kommentar: Eigentlich reicht Gl. (20) oder Gl. (21), weil
u
r
r
 B
E
 r  und  r 
 H
 D
 
 
über die MAXWELLschen Gleichungen miteinander verknüpft sind!
120