Lösung_1

Serie 1: Lösungen
1. (a) Ein Element der symmetrischen Gruppe S3 d.h. eine Permutation der
Grösse n = 3 ist definitionsgemäss eine Bijektion
σ: {1, 2, 3} → {1, 2, 3}
und kann als Abbildung tabellarisch in der Form
1 2 3
σ=
σ1 σ2 σ3
beschrieben werden, wobei σ(i) = σi ist. Oft gibt man der Einfachheit
halber nur die Folge (σ1 , σ2 , σ3 ) der verschiedenen Bild-Elemente an.
An der ersten Stelle können die 3 Elemente von {1, 2, 3} stehen. Dann
bleiben für die zweite Stelle wegen der vorausgesetzten Bijektivität
noch 2 Elemente zur Auswahl und das dritte Element ist damit eindeutig bestimmt. Insgesamt gibt es daher 3 · 2 · 1 = 3! = 6 verschiedene
Anordungen der Menge {1, 2, 3}. Somit besteht S3 aus den folgenden
Permutationen:
1 2 3
1 2 3
1 2 3
,
, σ2 =
, σ1 =
σ0 =
1 3 2
2 1 3
1 2 3
1 2 3
1 2 3
1 2 3
.
σ12 =
, σ21 =
, σ121 =
3 2 1
2 3 1
3 1 2
Diese 6 Permutionen können durch die beiden Vertauschungen σ1 und
σ2 benachbarter Elemente erzeugt werden, da σ12 = σ1 ◦ σ2 , σ21 =
σ2 ◦ σ1 gilt und σ121 = σ1 ◦ σ2 ◦ σ1 = σ2 ◦ σ1 ◦ σ2 ist.
(b) Damit lässt sich leicht eine Multiplikationstabelle der Gruppe (S3 , ◦)
aller Permutationen von 3 Elementen herstellen:
◦
σ0
σ1
σ2
σ12
σ21
σ121
σ0
σ1
σ2
σ12 σ21 σ121
σ0
σ1
σ2
σ12 σ21 σ121
σ1
σ0
σ12
σ2 σ121 σ21
σ2
σ21
σ0 σ121 σ1
σ12
σ12 σ121 σ1
σ21
σ0
σ2
σ21
σ2 σ121 σ0
σ12
σ1
σ121 σ12 σ21
σ1
σ2
σ0
Weil sie bezüglich der Diagonalen nicht symmetrisch ist, handelt es
sich um eine nicht-kommutative Gruppe. Sie lässt sich oft als BabyBeispiel einer Gruppe benutzen, weil es die kleinste Gruppe ist, in
der viele typische Phänomen gelten. Es gibt eine weitere, wesentlich
verschiedene Gruppe mit 6 Elementen. Die sogn. zyklische Gruppe Z6
wird in der Zahlentheorie besprochen.
Mit Hilfe der nächsten Aufgabe lassen sich diese Phänomene geometrisch veranschaulichen.
(c) Diese Permutationen liefern Kongruenzabbildungen des Raumes, indem man mit ihnen auf den drei Koordinaten operiert:
i. σ0 : (x, y, z) 7→ (x, y, z): Identität.
ii. σ1 : (x, y, z) 7→ (y, x, z): Spiegelung, deren Spiegelebene den Winkel
in der xy-Ebene halbiert und die z-Achse enthält.
iii. σ2 : (x, y, z) 7→ (x, z, y): Spiegelung, deren Spiegelebene den Winkel
in der yz-Ebene halbiert und die x-Achse enthält.
iv. σ12 : (x, y, z) 7→ (y, z, x): Drehung 120◦ um Achse OD.
v. σ21 : (x, y, z) 7→ (z, x, y): Drehung 240◦ um Achse OD.
vi. σ121 : (x, y, z) 7→ (z, y, x): Spiegelung deren Spiegelebene den Winkel in der xz-Ebene halbiert und die y-Achse enthält.
Sie sind längentreu, da sie aus den beiden Ebenenspiegelungen σ1
und σ2 zusamengesetzt werden können und diese Ebenenspiegelungen selbstverständlich längentreu sind, wie sofort aus dem Satz von
Pythagoras folgt.
(d) Betrachte die entgegengesetzten Drehungen
σ12 = σ1 ◦ σ2 6= σ2 ◦ σ1 = σ21
(e) Identifiziert man die Ecken des gleichseitigen Dreiecks mit den Elementen von {1, 2, 3}, so liefern die oben beschrieben Permutationen
die folgenden Kongruenzabbildungen des Raumes:
i.
ii.
iii.
iv.
v.
vi.
σ0 : Identität.
σ1 : Spiegelung an Höhe durch Ecke 3.
σ2 : Spiegelung an Höhe durch Ecke 1.
σ12 : Drehung 120◦ .
σ21 : Drehung 240◦ .
σ121 : Spiegelung an Höhe durch Ecke 2.
Das selbe Ergebnis erhält man auch, wenn man die drei Ecken des
Dreiecks mit den drei Einheitpunkten E1 , E2 , E3 identifiziert.
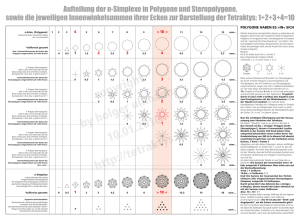
(f) Das reguläre Tetraeder hat 4 Ecken, 6 Kanten und 4 Seitenflächen. Die
Seitenflächen sind gleichseitige Dreiecke. Das Tetraeder hat folgende
Symmetrien:
• Identität (1)
• Drehung ±120◦ um jede Höhe (8)
• Drehung 180◦ um die Gerade durch gegenüberliegende Seitenmitten (3)
• Spiegelung, deren Spiegelebene eine Kante und die gegenüberliegende Seitenmitte enthält (12)
Insgesamt sind dies 24 Symmetrien. Wenn wir die 4 Ecken des Tetraeders mit {1, 2, 3, 4} identifizieren, werden die Symmetrien durch die
Permutationen aus Σ4 mit |Σ4 | = 4! = 24 beschrieben.
2. (a) Für die typischen Kongruenzabbildungen des Raumes erhält man:
i. 1 Ebene: Spiegelung an xy-Ebene (x, y, z) 7→ (x, y, −z).
ii. 2 Ebenen:
A. Translation: Spiegelungen an xy-Ebene und Ebene z = c, c
fest.
(x, y, z) 7→ (x, y, 2c)
B. Drehung 180◦ um z-Achse: Spiegelungen an xz-Ebene und yzEbene
(x, y, z) 7→ (−x, −y, z)
iii. 3 Ebenen:
A. Schubspiegelung:
(x, y, z) 7→ (x, −y, 2v)
B. Drehspiegelung:


cos(ϕ) − sin(ϕ) 0
0 
A =  sin(ϕ) cos(ϕ)
0
0
−1
Mit ϕ = 90◦ : (x, y, z) 7→ (−x, y, −z)
iv. 4 Ebenen: Schraubung: Komposition Translation und Drehung
(b) Die typischen Kongruenzabbildungen der Ebene sind aus der Ebenengeometrie bekannt und dienen zum Vergleich:
1 Gerade: Spiegelung
2 Geraden: Translation, Drehung
3 Geraden: Schubspiegelung
(c) Punktspiegelung pO in
R2 : Spiegelung sx an x-Achse: (x, y) 7→ (−x, y),
Spiegelung sy an y-Achse: (x, y) 7→ (x, −y),
sy ◦ sx : R2 → R2 ,
(x, y) 7→ (−x, −y)
R3 : Spiegelung sxy an xy-Ebene: (x, y, z) 7→ (x, y, −z),
Spiegelung syz an yz-Ebene: (x, y, z) 7→ (−x, y, z),
Spiegelung sxz an xz-Ebene: (x, y, z) 7→ (x, −y, z)
sxz ◦ syz ◦ sxy : R3 → R3 ,
(x, y, z) 7→ (−x, −y, −z)
(d) In R2 ist die Drehung um O mit dem Drehwinkel 180◦ , d.h. die Kongruenz pO = rO,180◦ = sy ◦ sx orientierungstreu.
(e) In R3 ist die Drehung um die y-Achse mit Winkel 180◦ , d.h. die Kongruenz syz ◦ sxy mit anschliessender Spiegelung an der xz-Ebene, d.h.
pO = sxz ◦ syz ◦ sxy eine orientierungsumkehrende1 Drehspiegelung.
3. siehe Skript p. 11 ff.
4. Wir gehen vom üblichen Schrägbild des (punktiert gezeichneten) Würfels
aus, um ihm nun regelmässig seine Ecken abzuschneiden und dadurch eine Reihe weiterer mehr oder weniger symmetrischer Polyeder zu erhalten,
die wir gelegentlich zur Illustration benutzen werden. Zur Berechnung der
Koordinaten wählen wir die Ecken des Würfels speziell in den Punkten
(±1, ±1, ±1).
Die Würfelkanten haben nach Voraussetzung die Länge a. Im numerischen
Spezialfall ist also a = 2. Diesem Würfel sollen nun alle Ecken regelmässig
abgeschnitten werden und zwar so, dass die abgeschnittenen Pyramiden die
Kantenlänge c haben. Zur Konstruktion der Schrägbilder braucht man einzig die Tatsache, dass die Parallelprojektion teilverhältnistreu ist. In obiger
Figur schneidet die rote Ebene von jeder der drei betroffenen Kanten 31 ab.
Daher ist in diesem Fall c = a3 . Entsprechendes gilt für die grüne Ebene,
mit der eine der benachbarten Ecken abgeschnitten wird. Die Aufgabe läuft
also konstruktiv darauf hinaus, die Würfelkanten im betreffenden Verhältnis zu teilen und den Überblick zu behalten, was durch Hervorheben der
sichtbaren und Stricheln der verdeckten Kanten geschieht.
1
Ein Rechtssystem geht in ein Linkssystem über.
Bei den gewählten Eckenkoordinaten des Ausgangswürfels haben die 8 Ebenen, mit denen je eine der Ecken abgeschnitten wird, die Gleichungen
±x ± y ± z = 3 − 2c
Je nach Wahl von c entstehen unterschiedliche Polyeder.
• Für 0 ≤ c ≤ a2 liegen alle Ecken des gesuchten Polyeders auf Würfelkanten und haben die Koordinaten
(1, 1, 1 − 2c), (−1, −1, 1 − 2c), (1, 1, 2c − 1), (−1, −1, 2c − 1)
(1, −1, 1 − 2c), (1, −1, 2c − 1)
und ihre Permutationen2 . Das sind in der Regel
3 + 3 + 3 + 3 + 6 + 6 = 24
Ecken. Als Grenzfälle für c = 0 bzw. c = a2 erhalten wir den Würfel
bzw. das Kuboktaeder. Dazwischen liegt der Würfelstumpf.
• Für a2 ≤ c ≤ a liegen alle Ecken des gesuchten Polyeders auf Mittellinien von Würfelseiten und haben die Koordinaten
(0, 1, 2 − 2c), (0, 1, 2 − 2c), (0, −1, 2c − 2), (0, −1, 2 − 2c)
und ihre Permutationen. Das sind in der Regel ebenfalls
6 · 4 = 24
Ecken. Als Grenzfälle für c = a2 bzw. c = a erhalten wir das Kuboktaeder bzw. das Oktaeder. Dazwischen liegt der Oktaederstumpf.
• Für a ≤ c ≤ 3a
2 schrumpft dieses Oktaeder und wird schliesslich zu
einem Punkt. Für noch grössere c ist das Schnittgebilde leer.
(a) Zunächst werden dem Würfel die 8 Ecken regelmässig so abgeschnitten, dass die Schnitteben durch die Kantenmitten geht, d.h. c = a2 ist.
Das entstehende Polyeder heisst Kuboktaeder und steht also gewissermassen zwischen Würfel und seinem dualen Oktaeder. Es hat e0 = 12
2
Selbstverständlich berechnet man nur gerade einen einzigen Punkt. Die restlichen ergeben
sich aus den (bekannten) Symmetrien. Das wichtigste Hilfsmittel, um die exponentielle Komplexität in höheren Dimensionen zu meistern, sind Symmetrien, deren Anzahl zum Glück mit
wachsender Dimension auch exponentiell zunimmt. Vor dem Jammern über einen zu grossen
Arbeitsaufwand kümmert man sich um die Symmetrien eines Problems.
Ecken, e1 = 24 Kanten und e2 = 14 Seitenflächen.
Seine Ecken haben bei obiger Wahl die Koordinaten
(0, ±1, ±1)
und ihre Permutationen. Man beachte, dass unter Parallelprojektionen kongruente Figuren nicht notwendigerweise in kongruente Figuren
abgebildet werden. Beispielsweise werden nicht alle kongruenten Quadrate des Würfels oder hier des Kuboktaeders auf kongruente Quadrate abgebildet. Streckenlängen, Längenverhältnisse auf verschiedenen
Geraden, Flächeninhalte und Winkel bleiben also, im Gegensatz zur
Parallelität und den Teilverhältnissen auf parallelen Geraden, unter
Projektionen in der Regel nicht erhalten. Ausnahmen sind die Quadrate auf der Vorder- und auf der Rückseite des Würfels. Sie werden
in wahrer Grösse abgebildet. Deshalb kann man an ihnen metrische
Verhältnisse ablesen.
(b) Weil die Vorderseite des Würfels in wahrer Grösse abgebildet wird,
können wir die Längenverhältnisse damit bestimmen. Dreht man die
Vorderseite um 45◦ um ihren Mittelpunkt, erhält man die folgende
ebene Hilfsfigur
c
√
c 2
c
Aus ihr kann man mit Hilfe des Satzes von Pythagoras sofort entnehmen, dass
√
√
c + c · 2 + c = (2 + 2)c = a
gelten muss. Auflösen liefert also
√
2+ 2
c=
a ≈ 0.293 · a
2
Eine leicht andere Begründung findet man in den Unterlagen, wo man
auch eine Abwicklung des entstehenden Würfelstumpfs findet, mit der
sich ein Modell für dieses Polyeder herstellen lässt. Man beachte, dass
das hier benötigte Verhältnis irrational ist. Weil es sich aber um eine
Zahl handelt, die auf rationale Art mit geschachtelten Qudratwurzeln
geschrieben werden kann, lässt sich auch von diesem Körper mit Hilfe
von Zirkel und Lineal ein Schrägbild konstruieren. Wie diese Überlegung zeigt, ist es wichtig, in solchen Ergebnissen Quadratwurzeln
stehen zu lassen und nicht einfach numerischen Zahlensalat hinzuschreiben. Zur Konstruktion kann man beispielsweise obige Hilfsfigur
benutzen. Der Würfelstumpf lässt sich also durch folgendes Schrägbild
darstellen.
(c) Im Fall c = 34 a entsteht auf analoge Weise ein Oktaederstumpf.
Er besteht aus 6 Vierecken und 8 Sechsecken. Aus Symmetriegründen
sind die Vierecke in den Würfelseiten Quadrate. Ferner erkennt man
leicht, dass die blau gefärbte Schnittebene die zugehörige Sechseckseite dreiteilt. Daraus folgt, dass auch die Sechsecke regulär sein müssen.
Auch zu diesem Polyeder findet man in den Unterlagen ein etwas anderes Vorgehen zur Konstruktion und zusätzliche Information. Man
beachte, dass der Oktaederstumpf im Gegensatz zum Würfelstumpf
durch rationale Koordinaten beschrieben werden kann.
(d) Für c = a erhalten wir das reguläre Oktaeder.
In den Unterlagen findet man eine Konstruktion des regulären Oktaeders als Flächenmittenkörper (Dualkörper) des Würfels.
(e) Jedes Polyeder, das aus dem Würfel durch regelmässiges Abecken entsteht, hat eine Umkugel, weil aus Symmetriegründen jede Ecke vom
Würfelmittelpunkt denselben Abstand hat. Um ihren Radius r zu berechnen, untersuchen wir die drei Fälle:
• Für 0 ≤ c ≤ a2 liegen alle Ecken auf Würfelkanten und der Abstand vom Kantenmittelpunkt beträgt a2 − c. Nach dem Satz von
Pythagoras ist
a 2 a 2 a
2 3a2
r2 =
−c =
− ac + c2
+
+
2
2
2
4
Das selbe Resultate erhält man aus den Koordinaten der Ecken.
• Für a2 ≤ c ≤ a liegen alle Ecken auf Mittellinien von Würfelseitenflächen und der Abstand vom Flächenmittelpunkt beträgt a − c.
Nach dem Satz von Pythagoras ist
a 2
5a2
r2 =
+ (a − c)2 =
− 2ac + c2
2
4
Das selbe Resultate erhält man aus den Koordinaten der Ecken.
Man beachte, dass die beiden Resultate im gemeinsamen Grenzfall
c = a2 für den Umkreisradius des Kuboktaeder den Wert
r2 =
liefern.
a2
2
• Für a ≤ c ≤ 3a
2 liegen alle Ecken auf Verbindungsstrecken gegenüberliegender Würfelseitenflächen. Der Abstand vom Würfelmittelpunkt beträgt
3a
r=
− c.
2
Das ist also der Umkugelradius. Dieses Resultat liefert im Grenzfall c = a für den Umkugelradius des Oktaeders das selbe Resultat
r = a2 wie das vorangehende und damit eine zusätzliche Möglichkeit zur Kontrolle.
(f) i. Selbstverständlich besitzt der Würfel für c = 0 eine Inkugel.
ii. Auch das Oktaeder besitzt für c ≥ a selbstverständlich eine Inkugel.
iii. Es gibt noch einen weiteren Fall, in dem das durch Abecken entstandene Polyeder eine Inkugel hat. Das ist nämlich auch dann
der Fall, wenn die Grundflächen der abgeschnittenen Pyramiden
die Inkugel des Würfels berühren. Um den zugehörigen Wert von
c zu bestimmen, kann man beispielsweise den folgenden Diagonalenschnitt betrachten.
√c
2
h
c
Das rechtwinklige Dreieck oben rechts hat√Katheten der Längen c
und √c2 und eine Hypotenuse der Länge c 2 6 .
√
√
Seine Höhe beträgt h = a2 3 − a2 = a2 · ( 3 − 1). Berechnet man
die doppelte Dreiecksfläche auf zwei Arten, erhält man
√
c
c 6 a √
c· √ =
· · ( 3 − 1)
2
2
2
und erhält daraus
c=
√
a
· (3 − 3) ≈ 0.634 · a
2
Alternativ gilt für den Schwerpunkt der Grundseite der Pyramide
beispielsweise in der Ecke (1, 1, 1) aus Symmetriegründen t(1, 1, 1)
2
mit t = 1 − 2c
3 . Für den Abstand zum Zentrum soll 3t = 1 gelten,
woraus ebenfalls c =
√
3− 3
2
folgt.
Auch dieses Verhältnis lässt sich mit Zirkel und Lineal konstruieren, obwohl es irrational ist. Beispielsweise kann man dazu obigen
Diagonalenschnitt verwenden. Das zugehörige Polyeder in folgender Figur besteht aus 6 Quadraten und 8 Sechsecken, die aber im
Gegensatz zu jenen des Oktaederstumpfes nicht regulär sind.