Martin Dressel, 1. Physikalisches Institut, Stuttgart: Die

Martin Dressel, 1. Physikalisches Institut, Stuttgart:
Die physikalischen Grundlagen der Supraleitung und
ihre geschichtliche Entwicklung
Zusammenfassung: Die Entdeckung der Supraleitung ist wohl das prominenteste Beispiel
dafür, dass lang vorbereitete und geplante Forschung zu ganz unerwarteten Ergebnissen gelangen kann, die nachhaltige Wirkung haben und sogar eine neues Gebiet begründen. Ausgehend von der Frage, wie sich Materie bei der Annäherung an den absoluten Nullpunkt von
T = 0 K = −273◦ C verhält, baute Heike Kamerlingh Onnes (1851-1926) an der Universität
Leiden gegen Ende des 19. Jhd. ein Laboratorium für Tieftemperatur-Technik und -Physik auf,
das zwanzig Jahre weltweit seinesgleichen suchte.1 Im Jahre 1908 gelang es ihm nach jahrelangen Bemühungen, das letzte permanente Edelgas Helium bei T = 4, 2 K zu verflüssigen.2 Bald
konnte flüssiges Helium als Kühlmittel eingesetzt werden, um andere physikalische Phänomene
zu untersuchen, wie die elektrische Leitfähigkeit von Metallen.
Hier sollen die wichtigsten physikalischen Phänomene der Supraleitung dargestellt und erklärt
werden: der verschwindende elektrische Widerstand, der perfekte Diamagnetismus, die Flussquantisierung, die Josephson-Effekte, der Isotopen-Effekt. Es werden die wichtigsten Modelle
und Theorien vorgestellt, wie die London-Theorie, das Zweiflüssigkeiten-Modell, die GinzburgLandau-Theorie, die BCS-Theorie, ohne dass in die mathematischen und physikalischen Details
gegangen wird. Schließlich werden die modernen Entwicklungen seit Entdeckung der Hochtemperatur-Supraleiter dargestellt sowie die wenigen technischen Anwendungen der Supraleitung in
Messtechnik und Industrie.
Elektrische Eigenschaften
Nach dem Ohm’schen Gesetz ist der elektrische Widerstand R definiert als das Verhältnis
der abfallenden Spannung U , wenn ein gewisser Strom I fließt (Abb. 1):
U =R·I
Länge L
.
(1)
Querschnittsfläche Q
Strom I
Spannung U
Abb. 1: Ein Metalldraht des Querschnitts Q wird vom Strom I durchflossen; nach einer Länge
L fällt die Spannung U ab. Der Widerstand des Drahtes ist dann das Verhältnis R = U/I.
Um die intrinsischen Eigenschaften des Metalls auszudrücken, die von der Länge L und
der Querschnittsfläche Q des Kabels nicht abhängen sollen, definiert man den spezifischen Widerstand ρ = RQ/L bzw. die elektrische Leitfähigkeit σ = 1/ρ. Dadurch läßt
sich das Ohm’sche Gesetz durch die elektrische Stromdichte j ausdrücken, die bei einem
elektrischen Feld E fließt:
j =σ·E .
(2)
Der spezifische Widerstand eines Metalls setzt sich zusammen aus Beiträgen der Stößen
der Ladungsträger (Elektronen) mit temperaturabhängigen Gitterschwingungen (Phononen) und den Stößen der Ladungsträger an Verunreinigungen, Fehlstellen und sonstigen
Gitterdefekten, welche temperaturunabhängig sind. Zu Beginn des 20. Jhd. war nicht klar,
was bei sehr tiefen Temperaturen zu erwarten sei. In Abb. 2 sind drei unterschiedliche
Varianten skizziert:
1. J. Dewar (1842-1923) vermutete (1904),3 dass der mit sinkender Temperatur abfallende metallische Widerstand schließlich für T → 0 K nach Null zu extrapolieren
sei (strichpunktierte Linie);
2. doch selbst wenn die Gitterschwingungen ausfrieren, sollten die Defekte zu einem
konstanten elektrischen Widerstand führen (A. Matthiessen, 1864) (punktierte Linie);4
3. wenn sich am absolut Nullpunkt aber nichts mehr bewegt, sollten auch die Elektronen lokalisieren und der Widerstand unendlich groß werden (Lord Kelvin (18241907), 1902) (gestrichelte Linie).5
Elektrischer Widerstand
0
Temperatur (K)
Abb. 2: Der spezifische Widerstand ρ(T ) kann bei tiefen Temperaturen entweder (1) verschwinden (Punkt-Strich-Linie) oder (2) aufgrund des Defektwiderstands einen konstanten Wert annehmen (punktierte Linie); (3) allerdings könnte die Bewegung der Elektronen auch einfrieren,
so dass der Widerstand divergiert (gestrichelte Linie).
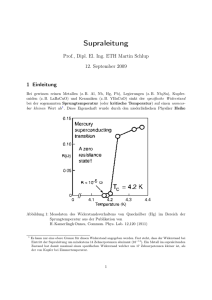
Die Frage konnte nur durch ein Experiment entschieden werden, das Kamerlingh Onnes und Mitarbeiter an dem Beispiel Quecksilber durchführen wollten, da das Metall bei
Zimmertemperatur flüssig ist, und deshalb gut gereinigt werden kann, um eine extrem
niedrige Rate an Verunreinigungen zu erhalten. Im Jahre 1911 berichtet Heike Kamerlingh Onnes in Leiden Communications,6 dass der Widerstand von Quecksilber bei einer
kritischen Temperatur Tc = 4.2 K schlagartig verschwindet, d.h. um vier Größenordnungen auf einen Wert kleiner 10−5 Ω absinkt. Dies war die Entdeckung der Supraleitung; im
Jahre 1913 erhielt Kamerlingh Onnes “für seine Untersuchungen der Eigenschaften von
Materie bei tiefen Temperaturen” den Nobelpreis.
Heute weiß man, dass die meisten Elemente des Periodensystems supraleitend werden,
wenn auch oft nur bei sehr niedrigen Temperaturen und unter hohem Druck. Gerade
die besten Leiter jedoch, wie Kupfer, Silber und Gold, zeigen keine Supraleitung, auch
nicht Edelgase. Interessant ist, dass die magnetischen Substanzen, wie Eisen, Kobalt und
Nickel, nicht supraleitend werden, ebenso wenig die meisten Lanthanide und Actinide,
diese Elemente sind auch als Seltene Erden bekannt. Die supraleitenden Eigenschaften
werden zunächst nicht beeinflusst, wenn das Material kein perfekter Einkristall ist, sondern polykristallin oder ein Film. Verunreinigungen sind in kleinen Mengen nur dann
relevant, wenn sie magnetisch sind.
Magnetische Eigenschaften
Ein Diamagnet wird aus dem Magnetfeld herausgestoßen, der Paramagnet hingegen wird
in das Magnetfeld hineingezogen. Diese magnetischen Eigenschaften sind allerdings sehr
schwach im Vergleich zu Ferromagneten, wie Eisen, Nickel oder Kobalt, die auch ohne
äußeres Feld – also permanent – magnetisch sind.
T = 300 K
Ba = 0
Ba
kühlen
kühlen
Ba = 0
Ba
T < TC
Ba
Abb. 3: Wird ein Supraleiter unterhalb der Sprungtemperatur abgekühlt und dann in ein Magnetfeld Ba gebracht, so wird dieses durch Abschirmströme komplett neutralisiert. Den gleichen
Zustand erreicht man, wenn man das Material in einem konstanten Magnetfeld abkühlt: im
normalleitenden Zustand dringt das Magnetfeld in das Metall ein, jedoch wird es unterhalb Tc
vollständig verdrängt, da der Supraleiter ein perfekter Diamagnet ist.
Während sich in Paramagneten die magnetischen Feldlinien verdichten, verdrängt ein
diamagnetischer Stoff die Feldlinien zu einem gewissen Grad. Ein Supraleiter ist jedoch ein
perfekter Diamagnet: unterhalb der Sprungtemperatur Tc wird das Magnetfeld aus dem
Supraleiter vollständig verdrängt. Nur in einer dünnen Haut der sogennanten Eindringtiefe
λ kann man sich supraleitende Ströme vorstellen, welche das magnetische Feld abschirmen.
Übersteigt die Feldstärke jedoch einen kritischen Wert Hc , so bricht die Supraleitung
zusammen, denn ein starkes Magnetfeld zerstört den supraleitenden Zustand.
Meißner (1882-1974) und Ochsenfeld (1901-1993) konnten 1933 zeigen,7 dass der gleiche
Effekt eintritt, wenn der Supraleiter in einem Magnetfeld unterhalb Tc abgekühlt wird.
Dies ist überraschend, da es mit dem verschwindenden Widerstand allein nicht erklärt
werden kann. Gemäß der klassischen Elektrodynamik (Faraday’sches Induktionsgesetz
∇ × E = − 1c ∂B
) werden Abschirmströme nur induziert, wenn sich das Magnetfeld zeitlich
∂t
ändert (Abb. 4). Hier bleibt es aber konstant; das Material geht nur vom metallischen in
den supraleitenden Zustand über, wie in Abb. 3 dargestellt. Die Beobachtung von Meißner
und Ochsenfeld bedeutet, dass die Supraleitung wirklich eine thermodynamische Phase,
ein neuer Grundzustand der Materie, ist.
Der verschwindende Widerstand ist zwar technisch sehr interessant, jedoch physikalisch
eher ein nachgeordnetes Phänomen. Physikalisch wichtiger und fundamentaler ist der
Meißner-Effekt, welcher auf das Wechselspiel von Supraleitung und Magnetismus hinweist,
das gerade bei den aktuellen supraleitenden Materialien der Oxide, der intermetallischen
Legierungen und eisenbasierten Systemen interessant ist.
(a)
B
(b)
B
N
J
S
S
Abb. 4: Es ist kaum möglich, zu beweisen, dass der Widerstand auf Null fällt. Heute kann
man durch Dauerringstromexperimente eine obere Grenze des spezifischen Widerstands von
ρ < 10−26 Ωm angeben. Hierbei wird ein Strom in einem Ring induziert. (a) Zieht man einen supraleitenden Ring aus einem Magnetfeld, wird ein Dauerstrom angeworfen (b), der nicht messbar
abfällt.
Im Jahre 1961 wurde diese Anordnung auch genutzt, um die Quantisierung des magnetischen
Flusses und damit von Cooper-Paaren nachzuweisen (siehe unten: Flussquantisierung). Macht
man den Ring sehr klein, so konnten Doll (*1923) und Näbauer (1879-1950) sowie Deaver (*1930)
und Fairbank (1917-1989) nachweisen, dass der darin eingeschlossene magnetische Fluss nur ein
ganzzahliges Vielfaches des Flussquants Φ0 = hc/2e sein kann.
Widerstand und Diamagnetismus
Diese beiden grundlegenden Eigenschaften, der verschwindende Widerstand und der perfekte Diamagnetismus, werden mit den London-Gleichungen beschrieben. Ausgangspunkt
des phänomenologischen Modells von Heinz (1907-1970) und Fritz London (1900-1954)8
aus dem Jahre 1935 bildet das Drude-Modell,9 d.h. eine Bewegungsgleichung für die Elektronen im Metall:10
d2 r m dr
= eE(t) ,
(3)
m 2 +
dt
τ dt
wobei e und m die Ladung und Masse des Elektrons, 1/τ die Streurate (wieviele Stöße pro
Sekunde stattinden), t die Zeit und r die Ortskoordinate sind. Der erste Term (Masse mal
Beschleunigung) beschreibt die Trägheit der Bewegung, der zweite die Reibungskraft und
angetrieben wird das Elektron durch die Coulomb-Kraft eE. Im Falle von Supraleitung
gibt es keine Reibung, sodass der zweite Term entfällt. Die Stromdichte ist hier gegeben
durch die Dichte der supraleitenden Ladungsträger ns mit der Elementarladung e und
deren Geschwindigkeit v, sodass
js = ns ev .
(4)
Anstelle des Ohm’schen Gesetzes ergibt sich somit
m ∂js
=E
ns e2 ∂t
;
(1. London-Gleichung)
(5)
durch das elektrische Feld nimmt der Strom mit der Zeit zu. In die Maxwell-Gleichungen
eingesetzt, erhält man eine Verknüpfung der zeitlichen Änderung des Magnetfeldes mit
dem Strom: ganz allgemein ist das magnetische Feld konstant, wenn kein Strom fließt,
doch konnten Meißner und Ochsenfeld zeigen, dass tief im Supraleiter das Magnetfeld
immer verschwindet:
∇×
m
1
js + B = 0 .
2
ns e
c
(2. London-Gleichung)
(6)
Der kreisförmige Abschirmstrom js kompensiert im Inneren gerade das Magnetfeld B.
(a)
normal
Leiter
z
(b)
Supraleiter
normal
Leiter
z
Supraleiter
ns
B
ns
B
ξ
ξ
λ
λ
x
x
Abb. 5: Ein statisches Magnetfeld kann in einem Metall konstant B sein, am Rande des Supraleiters fällt es jedoch exponentiell ab, wie durch die durchgezogenen Linien skizziert ist; die
London’sche Eindringtiefe λL gibt an, wo das Feld auf 1/e = 37% des ursprünglichen Werts
abgesunken ist.
Nach der Theorie von Ginzburg und Landau, die weiter unten beschrieben wird, nimmt am
Rande des Supraleiters auch die Dichte der supraleitenden Ladungsträger ns ab, wie durch den
gestrichelten Verlauf angedeutet; die charakteristische Länge ist hier die Kohärenzlänge ξ0 , was
als Abstand der Elektronen eines Cooper-Paars angesehen werden kann und dem Abstand entspricht, über welchen die Wellenfunktion des Supraleiters noch Kohärenzeigenschaften aufweist.
(a) Man spricht von Supraleitern des Typs I, wenn λL < ξ0 , wie beispielsweise in Hg, Al und
anderen Elementsupraleitern. (b) Die meisten der Legierungen und Hochtemperatursupraleiter
sind vom Typ II und die Eindringtiefe λL ist viel größer als die Kohärenzlänge ξ0 .
Neben einem perfekten Leiter ist der Supraleiter ein perfekter Diamagnet: er verdrängt
das Magnetfeld vollständig; allerdings geht dies nicht abrupt. Wird ein Supraleiter in ein
Magnetfeld gebracht, so dringt nur sehr wenig in das Material ein und fällt sehr schnell exponentiell mit B(x) = B(0) exp {−x/λL } ab, wie in Abb. 5 skizziert; die charakteristische
Länge ist die London’sche Eindringtiefe
√
λL =
mc2
4πns e2
,
(7)
welche für typische supraleitende Metalle nur 30 − 50 nm beträgt. In Gleichung 7 steht
m, ns und e für die Masse, Anzahl und Ladung der Ladungsträger sowie c für die Lichtgeschwindigkeit. In jüngster Zeit wurden viele exotische Klassen von Supraleitern, wie die
Kuprate, eisenbasierte oder organische Supraleiter entdeckt, die oftmals schlechte metallische Leiter sind und demzufolge eine bis zu hundertmal gößere Eindringtiefe zeigen.11
Zweiflüssigkeiten-Modell
Um die Temperaturabhängigkeit der Eindringtiefe zu beschreiben, macht man sich ein
einfaches Modell zunutze,12 das für die Beschreibung von superfluidem Helium entwickelt
wurde13 und von der Koexistenz von normalleitenden und supraleitenden Elektronen ausgeht: n = nn + ns . Mit abnehmender Temperatur gehen immer mehr Elektronen von
dem normalen Zustand nn in den supraleitenden ns über, wobei für T ≥ Tc natürlich
ns = 0 und für T = 0 alle Elektronen im supraleitenden Phase sind n = ns . Der Anteil der supraleitenden Ladungsträger ns in dem Material lässt sich ziemlich gut mit der
phänomenologischen Formel
(
ns
T
ns
=
=1−
n
nn + ns
Tc
)4
(8)
beschreiben und ist in Abb. 6 dargestellt. Erst unterhalb von ungefähr 31 Tc erreicht der
Supraleiter die gewünschte Perfektion.
Elektronen-Dichte ns, nn
1,0
ns / n
0,8
0,6
0,4
nn / n
0,2
0,1
0,0
0,2
0,4
0,6
0,8
1,0
Temperatur T / TC
Abb. 6: Temperaturabhängigkeit des Anteils von normalleitenden nn und supraleitenden Elektronen ns . Unterhalb der Sprungtemperatur Tc kondensieren schnell mehr und mehr Elektronen
zu Cooper-Paaren, sodass der Prozentsatz der normalleitenden Elektronen rasch abnimmt und
unterhalb von 0.5Tc falls völlig verschwunden ist.
Mittels Gleichung 8 kann nun die Temperaturabhängigkeit der Eindringtiefe
λ(0)
λ(T ) = √
1 − (T /Tc )4
(9)
mit λ(0) = λL der London’schen Eindringtiefe im Grenzfall T = 0 berechnet werden. Für
Aluminium ist beispielsweise λL = 50 nm, Hochtemperatur-Supraleiter wie YBa2 Cu3 O7
(siehe unten) erreichen hingegen λL = 120 − 800 nm, wobei die elektrischen Eigenschaften
dieser Materialien stark anisotrop sind, wie sich aus der in Abb. 11 gezeigten Kristallstruktur erklären lässt.
Flussschläuche
Wie schon in Abb. 5 angesprochen, teilt man die supraleitenden Materialien in zwei Klassen, genannt Typ I und II. In elementaren Supraleitern (Typ I) wie Hg, Al, In, Sn, etc.,
dringt das Magnetfeld gemäß den Gleichungen 7 und 9 nur am Rande in das Material ein.
Wird die Feldstärke zu hoch, bricht die supraleitende Phase plötzlich zusammen; das Material verhält sich wie ein gewöhnliches Metall und wird vom Magnetfeld durchdrungen. In
den meisten anderen supraleitendend Materialien (Typ II), d.h. Legierungen, Oxiden, Fullerenen und organischen Supraleitern, wird hingegen ein allmählicher Zusammenbruch der
diamagnetischen Eigenschaften beobachtet, denn es ist energetisch günstiger, wenn sich ab
einer Feldstärke Hc1 magnetische Flussschläuche (Vortices) bilden, welche erlauben, dass
an gewissen Stellen das Magnetfeld den Supraleiter durchdringt, wie in Abb. 7 dargestellt. Erst bei einer enorm hohen Feldstärke Hc2 wird die supraleitende Phase vollständig
Ha
H
λ
ξ
Flussschlauch-Kern
ns
r
B
j
Abb. 7: Skizze eines supraleitenden Films, der von dem äußeren Magnetfeld Ha durchdrungen
wird. Der Kern des Flussschlauchs (sogenannter Vortex) mit dem Radius der Kohärenzlänge ξ ist
normalleitendend. Hier ist das Magnetfeld B maximal, das im Abstand λ abfällt; Wirbelströme
j umschließen den Kern der Flussschläuche.
unterdrückt. In dieser Shubnikov-Phase (L.W. Shubnikov 1901-1937) wandern mit zunehmendem Feld Flüssschläuche vom Rande in das Material, die im Kern normalleitend
sind und ein magnetisches Flussquant Φ0 enthalten (s.u.), das wiederum über die Länge
λ abgeschirmt wird:
√
{
}
λ
−r
exp
.
(10)
B(r) ≈
r
λ
Da sie sich gegenseitig abstoßen, bilden sie ein auf A.A. Abrikosov ( 1928) zurckgehendes
hexagonales Abrikosov-Gitter, das mit Zunahme des Magnetfeldes immer dichter wird.14
Ginzburg (1916-2009) und Landau (1908)-1968) erkannten in ihrer phänomenologischen
Theorie,15 dass der supraleitende Zustand nicht homogen ist, sondern sich am Rande des
Tab. 1: Beispiele der charakteristischen Parameter für einige Supraleiter, der Sprungtem-
peratur Tc , der London Eindringtiefe λL , der Kohärenzlänge ξ0 , des oberen kritischen
Feldes Hc2 und der Energielücke 2∆.
Material
Tc
(K)
λL
(nm)
ξ0
(nm)
Hc2
(T)
2∆
(meV)
Al
Hg
Nb
Nb3 Ge
MgB2
YBa2 Cu3 O7
(TMTSF)2 PF6
κ-(ET)2 Cu[N(CN)2 ]Br
1,14
4,15
9,25
23,2
39
93
1,4
10.9
16
30
32
80
85 / 180
120 / 800
5 × 104
0,15 / 3, 8 × 104
1600
500
39
3
2,6 / 8
2 / 400
2.5 / 70
0,6 / 3,7
0,01
0,04
0,2
38
9 / 20
> 100
7
35
0,34
1,6
3,0
7
2,5 / 7,2
-
Materials oder der Flüssschläuche über einer Längenskala ξ ändert, die als Kohärenzlänge
bezeichnet wird und die Ausdehung der Wellenfunktion des supraleitenden Zustandes,
d.h. des Cooper-Paars, beschreibt. Das Verhältnis von Kohärenzlänge und Eindringtiefe ist in Abb. 5 dargestellt. Man kann sich also den Vortex als einen normalleitenden
Kern vorstellen, wo der Ordnungsparameter |ψ|2 = 0 und damit die Dichte der supraleitenden Ladungsträger verschwindet, und der den Radius der Kohärenzlänge ξ hat, wie
in Abb. 7 skizziert. Im Jahre 2003 empfing Abrikosov und Ginzburg zusammen mit A.
Leggett (*1938) für ihre “bahnbrechende Arbeiten in der Theorie über Supraleiter und Supraflüssigkeiten” den Nobelpreis. Landau hatte ihn schon 1962 “für seine bahnbrechenden
Theorien über kondensierte Materie, besonders das flüssige Helium” erhalten.
Mittels Kerr-Mikroskopie – d.h. der Drehung der Polarisation von Licht bei der Reflexion an einem magnetischen Material – kann man die Bewegung und Anordnung der
Flüssschäuche direkt beobachten. Hierbei sieht man, dass sie oft an Defekten hängen bleiben. Dies macht man sich bei der technologischen Anwendung Supraleitern für Elektromagnete zunutze, welche darunter leiden, dass Flussschlauchwanderungen zu Energieverlusten führen und letztendlich den Magneten zerstören können; der auftretende elektrische
Widerstand heizt das Material lokal auf, wo es dann normalleitend wird und noch mehr
Verluste erzeugt. Es werden deshalb künstlich sogenannte pinning oder Haft-Zentren beispielsweise durch Bestrahlung und Korngrenzen eingebracht, an denen die Flussschläuche
haften.
Flussquantisierung
Wenn in einem Ring der Strom erhöht wird, so nimmt der magnetische Fluss zu: Φ = B·Q,
wobei B das Magnetfeld und Q die umschlossene Fläche bezeichnen (Abb. 4). Schon 1948
überlegte F. London,16 was wohl passieren würde, wenn der Ring supraleitend ist und so
klein wird, dass die Gesetze der Quantenmechanik wichtig werden; der magnetische Fluss
im Ring ist quantisiert:
Φ=n
hc
= nΦ0
q
mit
n = 1, 2, ... ,
(11)
wobei Φ0 = hc
das elementare Flussquant wäre, das durch ein einzelnes Elektron kreiert
e
wird. Die Experimente, welche 1961 unabhängig von Deaver und Fairbank einerseits und
Doll und Näbauer andererseits durchgeführt wurden,17 erbrachten allerdings übereinstimmend den halb so großen Wert:
Φ0 =
hc
= 2 × 10−15 T m2
2e
;
(12)
d.h. der supraleitende Strom j wird durch ein Paar von Elektronen gebildet, ein sogennantes Cooper-Paar, das eben die doppelte Ladung trägt.18
Die Quantisierung des Magnetflusses bedeutet aber auch, dass der supraleitende Strom
in der Schleife quantisiert ist: der supraleitende Zustand wird durch eine makroskopische
Wellenfunktion der Ausdehnung ξ0 beschrieben. Anschaulich mag man sich dies als die
Wellenfunktion des Cooper-Paars vorstellen, strenggenommen ist es aber eine Vielteilchenwellenfunktion. Im Ring kann sich die Phase der Wellenfunktion nur um ein ganzzahliges Vielfaches von 2π ändern, um eine stabile Eigenfunktion zu bilden, analog zu
Stehwellen. Somit ist keine kontinuierliche Variation des Stroms möglich, sondern es sind
nur Sprünge erlaubt. Die Flussquantisierung belegt die quantenmechanische Natur der
Supraleitung, wirft aber die Frage auf, was denn die Elektronen zusammenhält, wenn sie
ein Cooper-Paar bilden.
Josephson-Effekt
Sind zwei Metalle durch eine extrem dünne Isolatorschicht von wenigen Nanometern getrennt, so kann trotzdem das ein oder andere Elektron durch die Barriere tunneln. Seit
den 1930er Jahren können Tunnelphänomene quantenmechanisch behandelt werden und
sind seitdem in jedem Physiklehrbuch zu finden. 1957 entwickelte Esaki die Tunneldiode
in hochdotierten Germanium-Halbleitern,19 wo die Elektronen in Sperrrichtung durch die
Energielücke des Halbleiters tunneln. Dieses Phänomen wurde im Jahre 1960 von Giaever
(*1929) auch in Supraleitern beobachtet und erklärt (Abb. 8).20 Seitdem ist es die Standardmethode, um die Energielücke im Supraleiter zu messen, aber auch die Zustandsdichte
und das Phononenspektrum.21 Abb. 9 zeigt die Temperaturabhängigkeit der Energielücke
für verschiedene Supraleiter.
Josephson (*1940) sagte nun 1962 voraus,22 dass nicht nur einzelne Elektronen sondern
auch ein supraleitender Strom, d.h. die Cooper-Paare, durch die Isolationsschicht tunneln
(a)
U
I
Au
Al
Al2O3
(b)
E
EF
2∆
U=0
T=0K
Strom I
Nn(E)
(c)
Ns(E)
E
EF
∆ = eU
Nn(E)
Spannung U
2∆
U = U1
Ns(E)
E
(d)
EF
Nn(E)
2∆
U = U2 > U1
Ns(E)
Abb. 8: Strom-Spannungskennlinie eines Tunnelkontakts zwischen einem Supraleiter (Al) und
einem Metall (Au). Erst wenn das elektrische Energie ∆ = eU überwunden ist, kann ein Strom
fließen. Aufgrund der divergierenden Zustandsdichte am Rande der Energielücke ∆ steigt der
Strom sehr schnell an.
können, was auch umgehend experimentell nachgewiesen wurde.23 Die dadurch realisierte
Josephson-Kopplung von zwei Supraleitern ermöglicht es, die beiden Wellenfunktionen
interferieren zu lassen. Wenn das Vektorpotential A räumlich konstant ist, hat der von
den Cooper-Paaren getragene Strom durch diese schwache Kopplung IJ die Größe
IJ = Ic sin ∆φ ,
(1. Josephson-Gleichung)
(13)
wobei ∆φ die Phasendifferenz der supraleitenden Wellenfunktionen beiderseits der Barriere darstellt und Ic der kritische Strom der Barriere ist. Die zeitliche Änderung der
Phasendifferenz führt zu einem Spannungsabfall U an dem Josephson-Kontakt
∂∆φ
2π
=
U
∂t
Φ0
,
(2. Josephson-Gleichung)
(14)
wobei das magnetische Flussquant Φ0 mit Gleichung 12 gegeben ist. Mit
2eU
(15)
h
erzeugt eine konstante Spannung von beispielsweise 1 mV einen supraleitenden Wechselstrom der Frequenz fJ = 483, 5979 GHz.
fJ =
Formt man gar einen Ring mit zwei solcher Josephson-Tunnelkontakten, so kann man den
darin eingeschlossenen Fluss sehr exakt messen; dies wird im Superconducting Quantum
1,0
∆(T) / ∆(0)
0,8
BCS
0,6
Zinn
Tantal
0,4
Blei
Niob
0,2
0,1
0,0
0,2
0,4
0,6
0,8
1,0
Temperatur T / TC
Abb. 9: Temperaturabhängigkeit der Energielücke für Sn, Ta, Pb und Nb. Die Temperatur
ist normiert auf die Sprungtemperatur Tc und die Energielücke auf den Wert bei T = 0. Die
durchgezogene Linie gibt die Vorhersage der BCS-Theorie wieder.
Interference Device (SQUID) auch kommerziell eingesetzt. Ändert sich das magnetische
Feld, so ändert sich der Strom im Ring und damit die Spannung am SQUID. Die FlussSpannungs-Kennlinie des SQUID ist periodisch und die Periode ist genau Φ0 .24 Esaki,
Giaever und Josephson erhielten für ihre bedeutenden Beiträge 1973 den Nobelpreis für
Physik.
Isotopeneffekt
Um festzustellen, ob Supraleitung ein rein elektronischer Effekt ist oder ob auch das
Kristallgitter beteiligt ist, führte schon Kamerlingh Onnes Messungen an verschiedenen
Isotopen durch, d.h. an Metallen, deren Atomkerne durch mehr oder weniger Neutronen schwerer oder leichter sind, die aber gleiche elektronische Eigenschaften haben. Erste
Experimente waren negativ, doch erst durch die Verfügbarkeit von Kernreaktoren und
Neutronenquellen sowie der Verbesserung der Isotopentrennung in den späten 1940er Jahren konnten vermehrt unterschiedliche Isotope von supraleitenden Metallen erzeugt und
untersucht werden.25 Der Nachweis der Abhängigkeit der Sprungtemperatur Tc von der
Kernmasse M
Tc ∝ M −0.5 ,
(16)
wie in Abb. 10 dargestellt, machte deutlich, dass das Kristallgitter für die Supraleitung
entscheidend ist.26 Es ist somit nachgewiesen, dass die attraktive Wechselwirkung zwischen den Elektronen durch Gitterschwingungen verursacht wird.27 Im Rahmen der BCSTheorie wird die Beziehung der Sprungtemperatur Tc zu der Debye-Frequenz ωθ und der
Zustandsdichte D(EF ) quantitativ hergeleitet:
{
−1
kB Tc = 1.14h̄ωθ exp
D(EF )V
}
,
(17)
4,18
Hg198
4,17
TC
4,16
Hg200,6
4,15
Hg200,7
Hg202
4,14
Quecksilber
4,13
4,12
Hg199,7
Hg
0,0700
203,4
0,0704
0,0708
0,0712
Masse (a.u.)-0,5
Abb. 10: Die Sprungtemperatur von verschiedenen Quecksilber-Isotopen fällt mit der Isotopenmasse ab. In der Auftragung von Tc als Funktion von (M )−0.5 erkennt man den linearen Anstieg
gemäß Gl. 16.
wobei V das Wechselwirkungpotential ist.
Dieser Mechanismus der Elektron-Phonon-Kopplung liegt allen metallischen Supraleitern
zugrunde, ebenso bei Fullerenen und MgB2 , und wurde erst mit der Entdeckung von Supraleitung in Schweren Fermionen (F. Steglich *1941) und organischen Materialien (D.
Jérome *1939) 1979 in Frage gestellt.28 In diesen Materialklassen findet man Supraleitung direkt neben einer magnetisch geordneten Phase, sodass es naheliegt, dass Spinfluktuationen für die Supraleitung mitverantwortlich sind. Dies gilt im weiteren auch für
Hochtemperatur-Supraleiter, wie die Kuprate und eisenbasierte Systeme. Dort ist Tc so
hoch, dass es gar die Debye Temperatur übersteigt Tθ = h̄ωθ /kB . In all diesen Materialien
hängt die Sprungtemperatur nur noch wenig von der Isotopenmasse ab.
BCS Theorie
In den 1950er Jahren kulminieren die Versuche einer theoretischen Beschreibung und
des Verständnisses der Supraleitung,29 an denen sich im wesentlichen alle maßgeblichen
Theoretiker beteiligt hatten. Nach vielen Jahren der intensiven Bemühungen gelang es
J. Bardeen (1908-1991) und seiner Gruppe (L.N. Cooper *1930, J.R. Schrieffer *1931)
mit einer umfangreichen Veröffentlichung30 zur “Theorie der Supraleitung” das Problem
endgültig zu lösen: die nach den Anfangsbuchstaben der Autoren benannte BCS-Theorie
wurde schnell anerkannt und gilt seitdem als Meilenstein in der Festkörpertheorie.31 Hierbei handelt es sich um eine Vielteilchentheorie, bei der sich durch die schwache anziehende
Wechselwirkung zweier Elektronen Cooper-Paare bilden.32 Zwar sind Elektronen aufgrund
ihres Spins 21 Fermionen, welche aufgrund des Pauli-Prinzips nicht den gleichen Zustand
einnehmen können; doch als Cooper-Paare – typischerweise mit Gesamtspin S = 0 (Singulett) aber ausnahmsweise auch S = 1 (Triplett) – formen sie Bosonen, die alle den
Grundzustand annehmen können und damit die Energie des Systems absenken. Diese
Vielteilchenwellenfunktion überdeckt den gesamten Festkörper und macht den Grundzustand der Supraleitung für lokale Störungen unempfindlich.
Die BCS-Theorie erklärt viele Beobachtungen, macht aber auch quantitative Vorhersagen,
die sich in den folgenden Jahren bestätigt haben; wie beispielsweise die Existenz einer
Energielücke
{
}
−1
∆0 ≈ h̄ωθ exp
(18)
D(EF )V
in der Zustansdichte. Hier ist wieder ωθ die Debye-Frequenz, D(EF )) die Zustandsdichte
an der Fermi-Kante (d.h. die mögliche Anzahl der Elektronen mit höchster Energie) und
V das Wechselwirkungspotential. Es ist die Energie
2∆0 = 3.53kB Tc
(19)
erforderlich, um ein Cooper-Paar aufzubrechen; diese Energie hat einen typischen Temperaturverlauf, der in Abb. 9 gezeigt ist, zusammen mit Beobachtungen an verschiedenen
Metallen. Neben Tunnelexperimenten konnten vor allem elektrodynamische Untersuchungen im Mikrowellen- und infraroten Spektralbereich diese Vorhersagen bestätigen.33 Die
Energielücke zeigt sich auch in der spezifischen Wärme, in Messungen der Ultraschallabschwächung, der Relaxationsrate der Kernspins. 34
Hochtemperatur-Supraleiter
Die Entdeckung supraleitender Kuprate durch Bednorz (*1950) und Müller (*1927)35 im
Jahre 1986 löste trotz der noch niedrigen Sprungtemperatur von nur 30 K eine unvergleichliche Euphorie und Aktivität in der Festkörperforschung aus, denn man erahnte
das Potential der Keramiken. Dies sind Übergangsmetalloxide in Perovskit-Struktur, die
typischerweise isolierend sind, aber durch ihre komplexe Kristallstruktur sehr viele Variationen erlauben (Abb. 11). Es ist nicht zu hoch gegriffen, wenn man darin ein neues
Kapitel der Festkörper- und Materialforschung sieht. Wenige Monate später konnte in
einer YBa2 Cu3 O7 mit Tc = 93 K eine Sprungtemperatur oberhalb des Siedepunkts von
Stickstoff (77 K) gefunden werden36 die in Hg1 Ba2 Ca2 Cu3 O8 in den darauffolgenden Jahren auf 134 K bei Normaldruck und 153 unter Druck gesteigert werden konnte.37 Dass die
beiden Entdecker wenige Monate nach der Veröffentlichung den Nobelpreis 1987 für Physik erhielten, bedeutet eine für die Schwedische Akademie ungewohnte und überraschende
Aktualität.38 Breite industrielle Anwendung erschien möglich, die sich allerdings bis heute
nicht realisieren ließ, denn wegen ihrer Sprödigkeit ist die Verarbeitung der Keramiken zu
elektrischen Bauteilen oder Drähten sehr schwierig.
Von wissenschaftlicher Seite eröffneten diese Systeme jedoch ein Gebiet ganz neuer Physik, das einen enormen Schub in experimentellen Techniken und theoretischen Modellen
CuO-Ketten
CuO2-Ebenen
Y
Ba
Ba
As
Fe
O
Abb. 11: (a) Kristallstruktur von YBa2 Cu3 O7−δ mit den CuO-Ketten und CuO2 -Ebenen.
(b) Kristallstruktur von BaFe2 As2 . In beiden Fällen ist die zweidimensionale Struktur erkennbar,
die zu sehr anisotropen Eigenschaften führt.
hervorbrachte, auch wenn bis heute die Hochtemperatur-Supraleitung weder verstanden
ist noch theoretisch beschrieben werden kann.39 Bei den Kupraten hat man es mit antiferromagnetischen Mott-Isolatoren zu tun, d.h. die elektronische Wechselwirkung ist
relativ groß und macht die Materialien elektrisch isolierend. Erst mit zunehmender Dotierung mit Ladungsträgern – typischerweise Löcher, die durch Sauerstoffdefizit in den
Kupferoxid-Ebenen erzeugt werden, aber teilweise auch Elektronen – nimmt die elektrische Leitfähigkeit zu und Supraleitung setzt ein; Tc steigt dann mit weiterer Dotierung
an, ehe es jenseits einer Maximalkonzentration wieder verschwindet.
Es kristallisierte sich bald heraus, dass der normalleitende Zustand oberhalb Tc bei weitem nicht dem eines konventionellen Metalls entspricht: die elektronischen Eigenschaften
in den Kupferoxidebenen und senkrecht dazu sind stark anisotrop, der Ladungstransport
ist hundertmal schlechter als in Metallen und lässt sich mit gängigen Transporttheorien
nicht beschreiben; die Fermi-Fläche weist in bestimmten Richtungen eine stark erniedrigte elektronische Zustandsdichte bei niedrigen Energien auf (Pseudoenergielücke); die Ladungsträger zeigen die Tendenz zur Modulation und Ordnung (Ladungsdichtewelle, Spindichtewelle, elektronische Nematizität). Aber auch die magnetischen Eigenschaften sind
von großer Wichtigkeit, da das Ausgangsmaterial ein Antiferromagnet ist, der eine Ordnung der Spins in den Kupferoxidebenen bevorzugt. Da alle Hochtemperatur-Supraleiter
in der ein oder anderen Weise dotiert sind, stellt sich auch die Frage der Unordnung.
Dies schlägt sich auch in den supraleitenden Eigenschaften nieder: die Kuprate bilden zwar
auch Cooper-Paare mit entgegengesetztem Spin, doch verschwindet die Energielücke in bestimmten Richtungen und die Wellenfunktion ändert das Vorzeichen zwischen zwei um 90◦
gedrehten Richtungen (d-Wellen Supraleitung), ganz im Gegensatz zu der konventionellen
s-Wellen Supraleitung in Metallen; dies ändert das Anregungsspektrum fundamental und
beeinflusst die meisten Phänomene der Supraleitung. Die attraktive Wechselwirkung der
Elektronen wird wohl durch Spinfluktuationen vermittelt, auch wenn der Einfluss des Git-
ters nicht unberücksichtigt bleiben kann. Man kann z.B. durch gezielte Anregung dieser
Gitterschwingungen kurzzeitig Cooper-Paare fast bis Zimmertemperatur bilden.40
Der Widerstreit von Magnetismus und Supraleitung gilt auch noch bei den Kupraten;
um so grösser war die Überraschung, als von Hosono (*1953) und seiner Gruppe 2006
Supraleitung in eisenbasierten Verbindungen entdeckt wurde;41 dies war wieder eine sensationelle und völlig unerwartete Entdeckung. Schnell wurden verwandte Klassen mit
Sprungtemperaturen über 50 K gefunden und die physikalischen Untersuchungen brachten
ein Wechselspiel einer Spindichtewelle und Supraleitung zutage. Insbesondere die Familie
des dotierten BaFe2 As2 (Abb. 11) ist Gegenstand von intensiven Untersuchungen, wobei sowohl Elektronen- als auch Lochdotierung sowie Druck bzw. isovalente Substitution
zur Supraleitung führen. Bei den starken magnetischen Ausgangsmaterialien ist es nicht
verwunderlich, dass Spinfluktuationen für den Mechanismus der Supraleitung verantwortlich ist, wobei die Symmetrie des Ordnungsparameters nicht abschliessend geklärt ist, da
mehrere Elektronenbänder an der Fermi-Energie liegen (d.h. verschiedene Elektronen mit
unterschiedlichem Impuls haben die höchste Energien und können an der Paarung teilnehmen). Hier sind sowohl experimentelle als auch theoretische Anstrengungen erforderlich.42
Dies ist eine enorme Herausforderung, welche wohl noch mehrere Jahre auf ihre Lösung
warten muss.
Technische Anwendungen
Die größte technische Bedeutung von supraleitenden Materialien liegt in der Herstellung
von Magnetfeldspulen, wie sie vor allem für Forschung und Medizin, aber auch in anderen
industriellen Bereichen benötigt werden. Mit seiner drei Jahre zuvor gegründeten Firma
Oxford Instruments gelang es M. Wood (*1927) im Jahre 1962, den ersten supraleitenden
Magneten auf den Markt zu bringen. Kommerzielle Magnete aus supraleitendem NbSn3
erreichen heute 22 Tesla. Indem man eine große Magnetfeldspule aus einer metallischen
Nioblegierung (15 Tesla) mit einem supraleitenden Magneten (12 Tesla) aus dem Hochtemperaturesupraleiter YBa2 Cu3 O7 füllt, konnten im Jahre 2015 insgesamt 27 Tesla erreicht
werden. Hybrid-Magnete aus normalleitenden Spulen in supraleitenden Magneten erreichen 38-45 Tesla im Dauerbetrieb. Die japanische Magnetschwebebahn SCMaglev, welche
im Jahre 2015 auf einer Teststrecke mit 603 km/h einen Geschwindigkeitsrekord aufstellte, nutzt supraleitende Magnete im Zug; der Bau eines längeren Streckennetzes wird noch
mehrere Jahrzehnte dauern.
Supraleiter finden auch beim Bau von Teilchen-Beschleunigern ihren Einsatz, nicht nur als
Magnete, sondern auch um Resonatoren zu bauen, denn die Güte ist deutlich besser als in
konventionellen Kupferresonatoren. In der Messtechnik haben supraleitende Elemente in
Form des SQUIDs (s.o. zum Josephson-Effekt) Einzug gehalten, um sehr genau kleine Ma-
gnetfelder oder Ströme zu messen. Schließlich kann man mittels des ac Josephson-Effekts
(siehe unten) ein Frequenz-zu-Spannung-Konverter konstruieren, der für die Eichung von
Spannungen als sogenanntes Josephson-Normal genutzt werden kann. Intensiv wird am
Einsatz von supraleitenden Filmen als Lichtempfänger (Einzelphotonen-Detektoren) im
infraroten und THz-Spektralbereich gearbeitet.
Der Einsatz von supraleitenden Strombegrenzern, induktiven Heizungen, Motoren oder
Roll-Lagern beschränkt sich im Moment noch auf wenige Versuchsmodelle und Nischenanwendungen; kommerzielle Serienproduktion gibt es nicht. Ebenso wurden bisher nur wenige Kilometer lange Stromleitungen aus Supraleitern verlegt, um den verlustfreien Stromtransport auf großer Skala zu demonstrieren.
Resümee
Das Phänomen der Supraleitung fasziniert zu Recht Wissenschaftler seit über hundert
Jahren, da es fundamentale Frage ebenso berührt, wie erstaunliche Materialeigenschaften
und nützliche Anwendungen.43 Als Vielteilchenphänomen des Festkörpers weist die Supraleitung eine große Komplexität in den Erscheinungen und der theoretischen Beschreibung auf. Die hier gewonnenen Erkenntnisse können auf andere Phänomene übertragen
werden. Trotz der enormen Fortschritte, ist es bei weitem kein abgeschlossenes Kapitel
der Festkörperphysik, denn einerseits werden immer neue Details entdeckt, andererseits
Materialklassen gefunden, die jenseits der bisherigen Erwartungen lagen. Hier werden
neue theoretischen Modelle entwickelt werden müssen, ehe ein grundlegendes Verständnis
möglich ist, wie dies die BCS-Theorie in konventionellen Supraleitern in beispielhafter
Weise geleistet hat. In den letzten Jahren ist man zudem dazu übergegangen, in künstlich
hergestellten Materialstrukturen, wie beispielsweise Grenzflächen von Oxiden, Supraleitung gezielt zu erzeugen. Dieser Bereich ist bei weitem noch nicht vollständig ausgereizt
und mag ein großes Potential in experimentalphysikalischer Erforschung, theoretischer
Behandlung, und technischer Anwendung beinhalten.
Zitierte Literatur
1
D. van Delft: Freezing physics-Heike Kamerlingh Onnes and the quest for cold, Amsterdam, Koninklijke Nederlandse Akademie von Wetenschappen, 2007 sowie hier den Beitrag von K. Hentschel.
2
H. Kamerlingh Onnes: The liquefaction of helium, Koninklijke Nederlandse Akademie von Wetenschappen, Proceedings 11, 1908-1909, Amsterdam 1908: 168-185 (= Communications from the Physical
Laboratory of the University of Leiden 108).
3
J. Dewar & J.A .Flemming: The Electrical Resistance of Metals and Alloys at Low Temperatures
Approaching the Absolute Zero, Philosophical Magazine 36 (1893): 271-299; J. Dewar: Collected Papers,
Cambridge: Cambridge University Press, 1927.
4
A. Matthiessen & M. von Bose: Über den Einfluss der Temperatur auf die elektrische Leitungsfähigkeit
der Metalle, Annalen der Physik und Chemie 191, 353-397 (1862); A. Matthiessen & C. Vogt: Über den
Einfluss von Spuren fremder Metalle auf die elektrische Leitungsfähigkeit des Quecksilbers, sowie: Antwort
auf die Bemerkungen des Hrn. R. Sabine zu dieser Arbeit, Annalen der Physik und Chemie 192 (1862):
369-392; A. Matthiessen & C. Vogt: Über den Einfluss der Temperatur und die elektrische Leitfähigkeit
der Legierungen, Annalen der Physik und Chemie 198 (1864): 19-78.
5
L. Hoddeson, E. Braun, J. Teichmann & S. Weart (Hrsg.) Out of the Crystal Maze: Chapters from
the History of Solid State Physics, New York & Oxford: Oxford University Press, 1992).
6
H. Kamerlingh Onnes, Communications from the Physical Laboratory of the University of Leiden
120b (April 1911); wiederabgedruckt in Koninklijke Nederlandse Akademie von Wetenschappen, Proceedings 13, 1274 (1911), Communications from the Physical Laboratory of the University of Leiden 122b
(May 1911); wiederabgedruckt in Koninklijke Nederlandse Akademie von Wetenschappen, Proceedings
14, 113 (1911) sowie Communications from the Physical Laboratory of the University of Leiden. Suppl.
29 (Nov. 1911). Siehe hierzu ferner den Beitrag von K. Hentschel sowie den Nobelpreisvortrag von H.
Kamerlingh Onnes in diesem Sammelband.
7
W Meißner & R. Ochsenfeld: Ein neuer Effekt bei Eintritt der Supraleitfähigkeit, Die Naturwissenschaften 21 (1933): 787-788.
8
H. London & F. London: The Electromagnetic Equations of the Supraconductor, Proceedings of the
Royal Society London A 149 (1935): 71-88.
9
P. Drude: Zur Ionentheorie der Metalle, Physikalische Zeitschrift 1 (1900): 161-165; Zur Elektronentheorie der Metalle, Annalen der Physik (1) 306 (1900): 566-613; Zur Elektronentheorie der Metalle: II.
Teil. Galvanomagnetische und thermomagnetische Effecte, Annalen der Physik 308 (1900): 369-402.
10
M. Dressel & G. Grüner: Electrodynamics of Solids: Optical Properties of Electrons in Matter, Cambridge: Cambridge University Press, 2002.
11
K.H. Bennemann & J.B. Ketterson (Hrsg.) Superconductivity, Bd. 1: Conventional and unconventional Superconductors, Bd. 2: Novel Superconductors, Berlin: Springer 2008.
12
F. London: Superfluids, New York: John Wiley & Sons 1954; J. Gorter: Progress in Low-Temperature
Physics, Amsterdam: North-Holland Publishing Company 1955, Kap. 1.
13
L. Tisza: The theory of quantum liquid application to helium liquid, Journal de Physique et le
Radium 1 (1940): 164-172 (1940) sowie: The theory of quantic liquids - Application on liquid helium II,
ibid. 350-358; L. Landau: The theory of superfluidity of helium II, Journal of Physics-USSR 5 (1941):
71-90.
14
A. A. Abrikosov: The magnetic properties of superconducting alloys, Journal of Physics and Chemistry of Solids 2 (1957): 199-208.
15
V.L. Ginzburg & L.D. Landau: On the Theory of Superconductivity, Zhurnal Eksperimental’noi i
Teoreticheskoi Fiziki 20 (1950): 1064-1082; Englische Übersetzung in: L. D. Landau: Collected papers,
Oxford: Pergamon Press, 1965, S. 546.
16
F. London:On the Problem of the Molecular Theory of Superconductivity, Physical Review 74, 562573 (1948).
17
B.S. Daever & W.M Fairbank: Experimental Evidence for Quantized Flux in Superconducting Cylinders, Physical Review Letter 7 (1961): 43-46; R. Doll & M. Näbauer: Experimental Proof of Magnetic
Flux Quantization in a Superconducting Ring, Physical Review Letters 7 (1961): 51-52.
18
L.N. Cooper: Electron Pairs in a Degenerate Fermi Gas, Physical Review 104 (1956): 1189-1190; vgl.
die anschaulichen Analogien dazu im Beitrag von K. Hentschel in diesem Band.
19
L. Esaki: New Phenomenon in Narrow Germanium p-n Junctions, Physical Review 109 (1957): 603-
604.
20
I. Giaever:Energy Gap in Superconductors Measured by Electron Tunneling, Physical Review Letters
5 (1960): 147-148; Electron Tunneling Between Two Superconductors, ibid., 464-466.
21
W. Eisenmenger & A.H. Dayem: Quantum Generation and Detection of Incoherent Phonons in
Superconductors, Physical Review Letters 18 (1967): 125-127.
22
B.D. Josephson:Possible New Effects in Superconducting Tunnelling, Physical Letters 1 (1962): 251-
253.
23
P.W. Anderson & J.M. Rowell: Probable Observation of the Josephson Superconducting Tunneling
Effect, Physical Review Letters 10 (1963): 230-232; J. M. Rowell: Magnetic Field Dependence of the
Josephson Tunnel Current, Physical Review Letters 11 (1963): 200-202.
24
J. Clarke & A.I. Braginski: The SQUID Handbook, Vol. 1: Fundamentals and Technology of SQUIDs
and SQUID Systems, Vol. 2: Applications, Weinheim: Wiley-VCH, 2004 & 2006.
25
E. Maxwell:Isotope Effect in the Superconductivity of Mercury, Physical Review 78 , 477 (1950); C.
A. Reynolds, B. Serin, W. H. Wright & L. B. Nesbitt:Superconductivity of Isotopes of Mercury, Physical
Review 78 (1950): 487.
26
H. Fröhlich: Theory of the Superconducting State. I. The Ground State at the Absolute Zero of
Temperature, Physical Review 79 (1950): 845-856; Theory of the Superconducting State: II Magnetic
Properties at the Absolute Zero of Temperature, Proceedings of the Physical Society, Section A 64 (1952):
129-134; Interaction of Electrons with Lattice Vibrations, Proceedings of the Royal Society (London) A215
(1952): 291.
27
J. Bardeen: Electron-Vibration Interactions and Superconductivity, Reviews of Modern Physics 23
(1951): 261-270; J. Bardeen & D. Pines:Electron-Phonon Interaction in Metals, Physical Review 99 (1955):
1140-1150.
28
F. Steglich, J. Aarts, C. D. Bredl, W. Lieke, D. Meschede, W. Franz & H. Schäfer: Superconductivity
in the Presence of Strong Pauli Paramagnetism: CeCu2 Si2 ”, Physical Review Letters 43 (1979): 1892-1895;
D. Jérôme, A. Mazaud, M. Ribault & K. Bechgaard: Superconductivity in a synthetic organic conductor
(TMTSF)2 PF6 , Journal de Physique Lettres 41 (1980): L95-98.
29
J. Schmalian: Failed theories of superconductivity, Modern Physics Letters B 24 (2010): 2679-2691;
J. Bardeen:Theory of Superconductivity. Theoretical Part, in: Handbuch der Physik 15, Berlin: Springer
1956, S. 274-369.
30
J. Bardeen, L.N. Cooper & J. Schrieffer: Theory of Superconductivity, Physical Review 108 (1957):
1175-1204.
31
L.N. Cooper & D. Feldman (Hrsg.) Bardeen, Cooper and Schrieffer: 50 Years, Singapore: World
Scientific 2010; Superconductivity, Bd. 1 & 2, herausgegeben von R.D. Parks, New York: Marcel Dekker
1969.
32
Anschauliche Analogien finden sich in K. Hentschels Beitrag in diesem Sammelband.
33
M. Dressel: Electrodynamics of Metallic Superconductors, Advances in Condensed Matter Physics
2013, 104379.
34
R. W. Morse & H. V. Bohm: Superconducting energy gap from ultrasonic attenuation measurements,
Physical Review 108 (1957): 1094-1096; L. C. Hebel & C. P. Slichter: Nuclear relaxation in superconducting aluminum, Physical Review 107 (1957): 901.
35
J.G. Bednorz & K.A. Müller: Possible High Tc Superconductivity in the Ba-La-Cu-O System”, Zeitschrift für Physik B 64 (1986): 189-193.
36
M. K. Wu, J. R. Ashburn, C. J. Torng, P. H. Hor, R. L. Meng, L. Gao, Z. J. Huang, Y. Q. Wang & C.
W. Chu: Superconductivity at 93 K in a New Mixed-Phase Y-Ba-Cu-O Compound System at Ambient
Pressure, Physical Review Letters 58 (1987): 908-910.
37
A. Schilling, M. Cantoni, J.D. Guo & H.R. Ott: Superconductivity above 130 K in the Hg-Ba-Ca-CuO system, Nature 363 (1993): 56-58; C.W. Chu, L. Gao, F. Chen, Z.J. Huang, R.L. Meng & Y.Y. Xue:
Superconductivity above 150 K in HgBa2 Ca2 Cu3 O8+δ at high pressures, Nature 365 (1993): 323-325.
38
Siehe hierzu auch das Gespräch von G. Grasshoff mit K. Bednorz sowie den Beitrag von K. Hentschel.
39
B. Keimer, S.A. Kivelson, M.R. Norman, S. Uchida & J. Zaanen: From quantum matter to hightemperature superconductivity in copper oxides, Nature 518 (2015): 179-186.
40
W. Hu, S. Kaiser, D. Nicoletti, C.R. Hunt, I. Gierz, M.C. Hoffmann, M. Le Tacon, T. Loew, B. Keimer,
& A. Cavalleri: Optically enhanced coherent transport in YBa2 Cu3 O6.5 by ultrafast redistribution of
interlayer coupling, Nature Materials 13 (2014): 705-711.
41
Y. Kamihara, H. Hiramatsu, M. Hirano, R. Kawamura, H. Yanagi, T. Kamiya & H. Hosono: IronBased Layered Superconductor: LaOFeP, Journal of the American Chemical Society 128 (2006): 10012-3.
42
J. Schmalian: Supraleitung: Unkonventionell und komplex, Physik Journal 10,6 (2011): 37-43 .
43
siehe das Themenheft des Physik Journals im Juni 2011; H. Rogalla & P.H. Kes (Hrsg.) 100 Years
of Superconductivity, Boca Raton: CRC Press, Taylor & Francis, 2012.
Verfasser: Professor Dr. rer. nat. Martin Dressel
1. Physikalisches Institut der Universität Stuttgart
Pfaffenwaldring 57, D-70550 Stuttgart, Germany
email: [email protected]