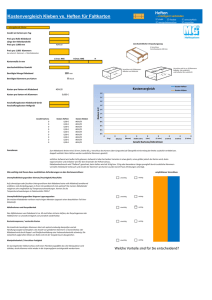
rot E = 0 div D = rot H = j div B = 0 ˙ div j = 0

5. Die Maxwell'schen Gleichungen
5.1. Der Verschiebungsstrom
rot 
E =0
rot 
H = j
bisher:
div 
D=
div 
B=0
Die Kontinuitätsgleichung (Ladungserhaltung) fordert:
̇  div j = 0
Wenn aber
da
rot 
H = j
dann muss gelten
̇ = 0 ,
div
rot 
H = div j .

0
Es fehlt offensichtlich ein Term, der diesen Widerspruch korrigiert.
115
rot 
H = j  ̇
D
Postulat:
div rot 
H = div j  div ̇
D=0
div j  ̇ = 0
Bedeutung:
̇
D
̇
D
= 0 ̇
E  ̇
P erzeugt ein Magnetfeld
= Verschiebungsstromdichte
rot 
H = Stromdichte + Verschiebungsstromdichte
d
P
: wird durch Ladungsträgerbewegung verursacht,
dt
d
E
: ist ein neuer Effekt (wesentlich für Wechselstrom).
dt
116
5.2. Das Faraday'sche Induktionsgesetz
Magnet wird an Spule heran bewegt
-> Induktion einer Spannung
=
∫

B ⋅d f
Fläche der
Ringspule
d
=∮
E ⋅d r
dt
Änderung des Flusses
erzeugt elektrisches Feld
Richtung von E ist durch die Lenz'sche Regel (entgegen der Ursache) gegeben.
j=σE
da eine Spannung in einem Leiter einen Strom verursacht
j erzeugt Magnetfeld Hs
Hs und HM sind entgegengesetzt gerichtet
―> Abstoßung
117
Um Strom zu erzeugen, muss Arbeit geleistet werden.
∮ E ⋅ d r
ist positiv (festgelegt durch Skizze)
d
d
 = ∫
B ⋅ d f
dt
dt
Faraday`sches
Induktionsgesetz
negativ
d
d

E
⋅d
r
=
= − ∫
B ⋅d f

∮
dt
dt
22. September 1791 Newington Butts
† 25. August 1867 bei Hampton Court
Ui =∮
E ⋅ d r =
induzierte Spannung
hat anderes Vorzeichen als früher
r2
 U  r1 − U  r2  = −∫ E ⋅d r
r1
Grund:
Induzierter Strom verursacht Spannung
früher: Spannung verursacht Strom
118
Anwendung des Stokes'schen Satzes
d 



E
⋅
d
r
=
rot
E
⋅d
f
=
−
B ⋅d f

∮
∫
∫
dt
rot 
E = −̇
B
Die differenzielle Form besitzt nicht die vollständige Information.
Zeitliche Änderungen von B verursachen einen Wirbel von E, aber auch die
Fläche kann zeitlich veränderlich sein.
∫ ̇B df
wäre nicht ausreichend, aus
rot 
E = −̇
B
ist dies nicht zu sehen.
Experimenteller Befund:
d 
B ⋅d f
∫
dt
ist richtig (Generator)
Stromerzeugung (Dynamo, Generator)
1866/7 technische Realisierung durch
Siemens
Ernst Werner von Siemens
13. Dezember 1816 in Lenthe bei
Hannover;
† 6. Dezember 1892 in Berlin
119
5.3. Das System der Maxwell'schen Gleichungen
rot 
H = j  ̇
D
div 
D=
rot 
E = − ̇
B
div 
B=0
Achtung:
Den Inhalt dieser Seite
sollten Sie zur Prüfung
wissen. Er ist absolut
notwendig (aber nicht
hinreichend).
Statik: alle Zeitableitungen Null, j = 0
Stationäre Ströme: alle Zeitableitungen Null, j ≠ 0
Materialgleichungen:

D = 0 
E
P 
E

B = µ0 
H 
M 
H
j = j  
E
Näherungen

D = 
E

B = µ
H
j =  
E
Kontinuitäts-Gleichung folgt direkt aus den Maxwell'schen Gleihungen:
rot 
H = j  ̇
D
̇  div j = 0
Kraft: Lorentz-Kraft

F = q
E  q v × 
B
120
Die Maxwell'schen Gleichungen wurden zwischen 1861 bis 1864 von James Clerk
Maxwell entwickelt.
●
●
Sie beschreiben in einer geschlossenen Form die Erzeugung von elektrischen und
magnetischen Feldern durch Ladungen und Ströme, sowie deren Wechselwirkung
und bilden die theoretische Grundlage der Elektrodynamik und der Elektrotechnik.
●
Die Maxwell'schen Gleichungen beinhalten:
●
das Ampère'sche Gesetz,
●
das Faraday'sche Gesetz
●
das Gauß'sche Gesetz
●
Das Zusammenfassen dieser Gesetze in eine einheitliche Theorie
und die Erkenntnis der Notwendigkeit des Maxwell'schen
Verschiebungsstromes aus theoretischen Überlegungen stellt eine
der herausragendsten Leistungen dar.
1931, zum hundertsten Jahrestag von Maxwells Geburt, beschrieb
Einstein das Werk Maxwells als „das Tiefste und Fruchtbarste,
das die Physik seit Newton entdeckt hat“.
James Clerk Maxwell
13. Juni 1831 in Edinburgh
† 5. November 1879 in Cambridge
121
5.4. Energie(erhaltungs)satz
Maxwell'sche Gleichungen
rot 
H = j  ̇
D
rot 
E = −̇
B
∣ ⋅
E Skalarprodukt
∣ ⋅
H
Subtraktion der Gleichungen

E ⋅rot 
H −
H ⋅rot 
E = j⋅
E
E ⋅̇
D
H ⋅̇
B
Es gilt:
−div  
E ×
H=
E ⋅rot 
H −
H ⋅rot 
E

−div  
E ×
H=
j ⋅
E

E ⋅̇
D
H ⋅̇
B
Joule'sche Wärme 
Falls D = ε E und B = µ H
(falls nicht: siehe Landau/Lifschitz: Elektrodynamik der Kontinua VIII)
122
−div  
E ×
H  =   
E ⋅̇
E  µ
H ⋅̇
H
da
d  
 H ⋅ H  = ̇
H ⋅
H 
H ⋅̇
H = 2
H ⋅̇
H
dt

−div  
E ×
H=
2
1
=
2
d  
 E⋅ E   µ
dt
2
d  
 E⋅D   1
dt
2
d  
 H ⋅H 
dt
d  
 H ⋅B 
dt
elektromagnetische Energiedichte:
w = w el  w mag =
1  1 
E ⋅D  H ⋅ B
2
2
ẇ  div  
E ×
H  = −
Energiesatz der
Elektrodynamik
123
Definition: Poynting-Vektor

S =
E ×
H
John Henry Poynting
9. September 1852 in
Monton
† 30. März 1914 in
Birmingham
Für Nichtleiter σ = 0 -> ν = 0
ẇ  div S = 0
Energieerhaltungssatz
Die Energiedichte kann sich nur ändern, wenn ein Energiestromes fliesst.
—> Poynting-Vektor = Energiestromdichte in Richtung des Energieflusses
In isotropen optischen Medien ist der Poynting-Vektor parallel zum Wellenvektor. In
anisotropen optischen Medien, zum Beispiel in doppelbrechenden Kristallen, gilt dies
im allgemeinen nicht.
(Der Poynting-Vektor beschreibt 3 der 10 unabhängigen Komponenten des EnergieImpuls-Tensors des elektromagnetischen Feldes in der Relativitätstheorie.)
ν ≠ 0 Elektromagnetische Energie kann in Wärme umgewandelt werden
Damit existiert kein Erhaltungssatz für elektromagnetische Energie.
124
5.5. Die Wellengleichung
Radiowellen -> Licht -> Röntgen -> Gamma-Strahlung sind elektromagnetische Wellen
●
●
Voraussetzungen für die Herleitung der Wellengleichung:
●
µ, ε sind zeitliche und räumliche skalare Konstanten
●
ρ = 0 keine freien Ladungen
●
σ = 0 keine Leiter (nicht leitfähig)
●
aus Maxwell:

D = 
E, 
B = µ
H
rot 
H =  ̇
E
rot 
E = −µ ̇
H
div 
E =0
div 
H =0
- eine der Gleichungen mit rot nehmen und rot rot bilden
rot rot 
E = − µ rot ̇
H = −µ  ̈
E

E = grad div
E − rot rot E
0
2
2
∂
E
1
∂
E

E = µ 2 = 2
∂t
c ∂ t2
1
Lichtgeschwindigkeit
=

µ
in Medien mit ε, µ}
c2
1
= 0 µ0
2
c
Wellengleichung
Vakuum c
125
2
2
∂
E
1
∂
E

E = µ 2 = 2
∂t
c ∂ t2
Lösung einer linearen, partiellen Differenzialgleichung;
allgemeine Lösung ist eine ebene Welle
Re 
E : physikalisch sinnvoll


E  r ,t  = 
E 0 e i  k⋅r − t
x
x
E0 selbst kann komplex sein: E 0 = ∣E 0 ∣⋅e
i x
,
E 0y = ∣E 0y ∣⋅e i  ,
y
E 0z = ∣E 0z ∣⋅e i 
z
∣E 0x ∣=  Re E 0x 2  Im E 0x 2
Damit gilt ausführlich Re E
E x  r , t = ∣E 0x∣cos k⋅r −t x 
E y  r ,t  =∣E 0y∣cos k⋅r − t y 
E z  r , t = ∣E 0z∣cos k⋅r − t z 
126
Überprüfen unseres Lösungsansatzes:
∂ 
E = −i  
E
∂t


E=
E 0 ei  k⋅r − t
∂ 
E = i k x 
E
∂x

∇⋅
E =i
k⋅
E
2
2

E = 
∇ 
E = −k 
E
Damit folgt für unsere Wellengleichung

E=

1 ̈
E
2
c

1
−k 2 
E = 2 - 2  
E
c
2

k 2 −

E=0
2
c
Wir suchen eine nichttriviale
Lösung mit E ≠ 0
2

2
 
k = 2
c
 = c∣k∣ für beliebige Vektoren 
k ,
E0
127
Bedeutung von ω:
z. B. x-Komponente
Re E x
E x  r , t = ∣E 0x∣cos k⋅r −t x 
Der Kosinus ist eine periodische Funktion, die Periode ist τ:
 = 2
Kreisfrequenz ω:
f =
1

Frequenz
2
=
= 2 f

Bedeutung von k:
Wir wählen ein
k = k x , 0 , 0
cosk x x − t   x 
Die Wellenlänge λ ergibt sich aus kx λ = 2 π
kx =
2

falls 
k in x-Richtung
128
Allgemein gilt:
2
∣k∣= k =

 = c k ⇒ 2 f = c
2

f =c
Ebene Wellen


E=
E 0 ei  k⋅r − t 
Warum wird die obige Lösung ebene Welle genannt?
Für konstante Zeit t: k gegeben
k⋅r = const.

1 lineare Gleichung für x, y, z
Ebenengleichung

k
ist ein konstanter Vektor auf der Ebene, der
e =
k
in Ausbreitungsrichtung der Welle zeigt.
129
t = beliebig:
E ist konstant auf einer Ebene, die sich
mit Geschwindigkeit c in Richtung k bewegt.
k⋅r = k⋅r0 =  t
da r0 ∥ k
k r 0 = t
r0 =

t = ct
k
unendlich ausgedehnter
Lichtstrahl
Eine ebene Welle ist eine Welle, deren Wellenfronten Ebenen
konstanter Amplitude sind,die sich geradlinig ausbreiten.
130
Allgemeine Lösung:
Durch Überlagerung von ebenen Wellen lassen sich beliebige andere Wellen
darstellen. Die Superposition ist möglich, da die Maxwell'schen Gleichungen
lineare DGL sind, so dass die Summe von Lösungen wieder eine Lösung ist.


E  r ,t  = ∫ 
E 0  k  e i k⋅r − t d 3 k
E0(k) ist die Amplitude, welche von Richtung und Frequenz abhängen kann.
Welchen Charakter (transversal oder longitudinal) haben die Wellen?
Es gilt immer noch ε = skalar = const. und ρ = 0.
 =0
div 
E =
∇⋅
E =i
k⋅E
k⋅
E =0

E ⊥ zur Ausbreitungsrichtung
Ebene Wellen sind transversale Wellen, das elektrische Feld schwingt
senkrecht zur Ausbreitungsrichtung.
131
Bemerkungen
●
●
Röntgen hielt seine Strahlen noch für longitudinales Licht.
Falls ε ein Tensor
k  
E = 0 i. Allg. k nicht senkrecht zu 
E
anisotropes Medium (nicht kubischer Einkristall)
Wellen haben longitudinale Anteile —> Doppelbrechung
●
ρ ≠ 0 (z. B. Ionosphäre)
div  
E=



i k⋅E =

--> longitudinale Schwingungen --> „Plasma-Schwingungen“
Wilhelm Conrad Röntgen
27. März 1845 in Lennep
(heute Stadtteil von
Remscheid)
† 10. Februar 1923 in
München
Nobelpreis Physik 1901
Wellen werden charakterisiert durch:
●
Amplituden: |E0x|, |E0y|, |E0z|
Nur zwei sind unabhängig, da 
E⋅
k = 0,
in Ausbreitungsrichtung ist die Amplitude Null.
●
Wellenlänge λ und Frequenz f
●
2 Phasen
●
Polarisation (linear, zirkular, elliptisch)
132
Polarisation elektromagnetischer Wellen
a) linear polarisiert mit k || z
E0y y
Phasen αx = αy
x
x
E0
E x  r , t = ∣E 0x∣cos k⋅r −t x 
E y  r ,t  =∣E 0y∣cos k⋅r − t y 

E = E 0x ex  E 0y ey
E x =∣E 0x∣cos 
k⋅r −t
E y =∣E 0y∣cos k⋅r − t
 = ∣E 0x∣ex ∣E 0y∣ey  cos k⋅r− t
E

orts- und zeitunabhängig
feste Richtung von E
(Polarisations-Richtung)
y
tan  =
∣E 0∣
∣E 0x∣
133
b) zirkular (Phasen αx – αy = ± π/2)
x
y
∣E 0∣=∣E 0∣= E

E = E  cos k x− t e x ∓sink z −t 
für fester Raumpunkt = Parameter-Darstellung
 Kreis

 =
k aus
Eheu
 =−
2
2
x
Blickrichtung
im pos. z
E-Vektor durchläuft einen Kreis vom Radius E
mit Winkelgeschwindigkeit ω in einer Ebene
senkrecht zur Ausbreitungsrichtung
c) elliptisch: beliebige Phasendifferenz,
x
z
k
x
∣E 0∣ ≠ ∣E 0∣
134
Wie sieht das H-Feld aus?
 =−µ ̇
rot E
H
 = ̇
rot H
E
 = rot ̇
rot rot H
E=−µ  ̈
H
 =grad div
 − H

rot rot H
H

0
2
 1 ∂2 H

∂
H

 H =µ 
= 2
2
∂t
c ∂ t2
mit der ebenen Welle als Lösung
  r ,t = H 0 e i k⋅r −t 
H
 =0
wegen div H

k⋅H
 =0
mit =c∣k∣
 ⊥ k
H
Ausbreitungsrichtung
Zusammenhang zwischen E und H:
 =−µ ̇
rot E
H
 = 1 k × E

H
µ
 =i  µ H

i k × E
⇒
 ⊥ k und H
 ⊥E

H
135
Für den Betrag von |H| gilt damit:

k∣∣E∣
 ∣  µ
 ∣
∣E

∣
E∣

∣
∣H∣=
= =
= ∣E
µ
µ
µ µc
Für die Energiestromdichte erhalten wir:
 
k × 
E
1   




S= E × H = E ×
=
E × k × E 
µ
µ
 = 
 − C
 

Es gilt: 
A× 
B×C
B 
A⋅C
A⋅B
 2 heißt hier Re 
 
E
E ⋅Re E

1  2   
k 2 k

 2= 1 E
 2 e
S=
[ k  E  − E 
k⋅E  ]=
E =
e E
µ
µ
µ
cµ
0


µ
µ
2
 D=E

 
E⋅
D=
H 
H =µ H =H B= H⋅
B


1
1    
⇒ w el =w mag = w
w=  E
⋅D  H⋅B 
2
2
1  

 = e c w
S = e
E⋅D = e c 
E⋅D
µc
Elektromagnetische Energie strömt mit Lichtgeschwindigkeit in Ausbreitungs136
richtung der Welle.
Definition: Brechungsindex n
c vak
1
1
1
c=
=
=
    r r  0 0 n
n=  r  r
Der Brechungsindex n ist das Verhältnis zwischen der Geschwindigkeit des
Lichtes im Vakuum und seiner Geschwindigkeit c im jeweiligen Medium.
Meta-materialien = Material mit negativem Brechungindex
1964 sagte der sowjetische Physiker Victor Veselago die Existenz von Materialien mit
negativen Brechzahlen voraus. Würde die Herstellung eines solchen Materials gelingen, könnte
man damit Linsen herstellen, deren Auflösungsvermögen weit besser wäre als das von Linsen
aus gewöhnlichen optischen Werkstoffen.
Forschern um Srinivas Sridhar von der Northeastern University in Boston gelang es, einen
Verbundwerkstoff herzustellen, der ein feines Gitter aus Metalldrähten enthält, das für
Mikrowellen eine negative Brechzahl zeigt.
Im Oktober 2003 hat eine Gruppe um Yong Zhang in Colorado entdeckt, dass Kristalle aus
einer Legierung von Yttrium, Vanadium und Sauerstoff eine negative Brechzahl für Lichtwellen
eines großen Frequenzbereichs aufweisen. Der Kristall besteht aus zwei ineinander
geschachtelten Kristallgittern mit symmetrischen optischen Achsen. Die negative
137
Lichtbrechung tritt aber nur in einem gewissen Winkelbereich des Einfallswinkels auf.
Eigenschaften von normalen und negativ brechenden Medien
Ein halb in Wasser
getauchter Bleistift
erscheint geknickt, weil der
Brechungsindex von Wasser
höher ist als der von Luft.
Wenn Licht von einem
Medium mit niedrigem
Brechungsindex n in eines
mit höherem Index
übergeht, wird es zur
Normalen hin gebrochen.
Ein Objekt, das sich in
einem Medium mit positivem
Index vom Beobachter
entfernt, erscheint infolge
des Doppler-Effektes
röter.
In einem negativ brechenden
Medium wird der Bleistift
scheinbar komplett aus dem
Medium heraus geknickt.
Wenn Licht von einem Medium
mit positivem Brechungsindex in
eines mit negativem Index
übergeht, wird es komplett
zurück zu derselben Seite der
Normalen gebrochen.
In einem Medium mit
negativem Index
erscheint ein sich
entfernendes Objekt
blauer.
138
Ein geladenes Objekt, das sich
in einem positiv brechenden
Medium schneller als die darin
geltende Lichtgeschwindigkeit
bewegt, erzeugt einen Kegel
aus Cerenkov-Strahlung in
Vorwärtsrichtung.
In einem negativ
brechenden Medium
weist der Kegel
rückwärts.
In einem Medium mit positivem
Index wandern die Berge und
Täler eines elektromagnetischen Pulses in dieselbe
Richtung wie der gesamte Puls
und die Energie.
In einem negativ brechenden
Medium wandern die Einzelschwingungen entgegengesetzt
zum Gesamtpuls und zur
Energie.
139
normales Material
Ein elektrisches Feld
(grün) erzeugt eine
geradlinige Bewegung der
Elektronen (rot).
Ein Magnetfeld (violette Pfeile)
induziert eine kreisförmige
Bewegung der Elektronen.
Metamaterial
Realisierung eines Metamaterial
Geradlinige Ströme
(rote Pfeile) fließen in
parallel angeordneten
Drähten
Kreisförmige Ströme fließen
in Spaltringresonatoren; diese
können auch quadratisch sein.
Die Drähte und Resonatoren
müssen kleiner als die
Wellenlänge der elektromagnetischen Strahlung sein.
140
Anwendungen von Materialien mit negativem Brechnungsindex
Superlinse
Eine rechteckige Platte aus Material mit negativem Brechungsindex
wirkt als Superlinse. Das von dem Objekt (links) ausgehende Licht
(blaue Linien) wird an der Oberfläche der Linse gebrochen und
vereinigt sich innerhalb der Platte zu einem spiegelverkehrten Bild.
Beim Austritt aus der Platte wird das Licht erneut gebrochen und
erzeugt ein zweites Bild (rechts). Bei einigen Metamaterialien enthält
das Bild sogar Details, die kleiner sind als die verwendete Wellenlänge.
Tarnkappe (für Mikrowellen)
Vor kurzem gelang die Realisierung einer (2D) Tarnkappe
für Mikrowellen. Das Objekt ist für MW einer
bestimmten Frequenz unsichtbar. Ähnliches wurde auch
schon für rotes Licht durch ein gitterartiges Material aus
Silber erreicht, das mit Löchern von 100 nm einen
Brechungsindex von -0,6 bei 780 nm Wellenlänge besitzt.
„Metamaterial Electromagnetic Cloak at Microwave
Frequencies“, D. Schurig et al.,
Science (2006): 314, 977 - 980
141
Ändert sich beim Durchgang zu einem anderen Medium die Wellenlänge λ oder
die Frequenz f?
Die Frequenz bleibt konstant, da E ~ eiωt. Um die Randbedingungen für alle Zeiten t
zu erfüllen, muss deswegen gelten ωinnen = ωaußen.
--> λ ändert sich, da w=ck gilt erhalten wir
c vak k vak =c k
(im Stoff z.B. Glas)
k =n k vak

 = vak
Wellenlänge wird kürzer, n > 1
n
142
Der Wellenwiderstand charakterisiert, wie sich eine Welle in einem Medium
fortpflanzt.
Bildlich entspricht dies der Härte oder Weichheit, die das Medium der sich
ausbreitenden Welle entgegensetzt.

E
µ
=
H

µ
Z 0 = 0 =377 
0
Def. Wellenwiderstand: Z =

Vakuum:
Aus dem Zusammenhang zwischen E und H erhalten wir:
k × 

E = µ H
k E= µ H
E µ
µ
µ
=
= µ c=
=
H
k
 µ 

Widerstandstypen:
●
Ohmscher Widerstand
●
Wechselstromwiderstände (Kapazitäten, Induktivitäten, Impedanz)
●
Wellenwiderstand bei Hohlleitern (wichtig für Anpassung damit es nicht zu
Reflexionen kommt, z.B. Netzwerke 50 Ω)
●
143
5.6. Wellen in Materie (mit Absorption): Telegrafengleichung
Bisher hatten wir ebene Wellen als Lösung der Wellengleichung.
E= E0 e i k⋅r − t 
x
E x =E 0 cos k⋅r −t x 
Da die Energiedichte proportional zum Quadrat der elektrischen Feldstärke ist, muss
sich die Amplitude ändern, wenn Absorption auftritt.
●
Welche Voraussetzung bei der Herleitung der Wellengleichung ändert sich in Materie?
●
µ, ε konstante Skalare
●
ρ = 0 auch erfüllt
●
σ = 0 ist nicht erfüllt.
Wichtig ist die Frequenzabhängigkeit, entscheidend ist die Leitfähigkeit bei der
Frequenz der sich ausbreitenden Welle, so kann σ(ω=0) = 0, aber σ(ωLicht) ≠ 0.
●
 =−̇
rot E
B
 = E
  ̇
rot H
E
 =−µ rot ̇
rot rot E
H =−µ ̇
E  ̈
E
da rot rot=grad div−
2


1
∂
E
∂E

 E= 2
µ 
2
∂t
c ∂t
Telegrafen-Gleichung
144
2


1
∂
E
∂E

 E= 2
µ 
2
∂t
c ∂t
Analogie aus der Mechanik:
Die erste Zeitableitung gibt eine Geschwindigkeit, Reibungskräfte sind
proportional zur Geschwindigkeit.
Reibung = Dämpfung einer Bewegung
∂
E

Absorption
∂t
Die Telegrafengleichung ist nicht mehr Zeit invariant, d.h. die
Symmetrie (t -> – t) ist zerstört. Absorption ist ein irreversibler Prozess.
Die Lösung der Telegrafengleichung wird wieder durch einen ebenen Wellen
Ansatz gesucht.
 r , t = E0 e i  k⋅r − t 
E

∂E
∂
E


~ −i  E
~ i kx E
∂t
∂x
 −k 2 E

E
Einsetzen des Ansatzes gibt eine Bedingung, wann der Ansatz eine Lösung ist:
2

 =−


−k E
E−i  µ  E
2
c
2
145
Nur die nichttriviale Lösung mit E ≠ 0 ist von Interesse:
2

2
k = 2 i   µ
c

2

k = 2 i  µ=i 
c
Damit erhalten wir rein formal einen komplexen Wellenvektor k. Anstatt eines
komplexen k, führen wir einen komplexen Brechungsindex ñ ein.
k = k vak n
n =ni 
Um die Ausbreitungrichtung der Welle zu bezeichnen führen wir einen
Einheitsvektor e in Ausbreitungsrichtung ein.
i  e⋅r k


E = E0 e
vak
n − t 
−e⋅r k 
i  e⋅r k

=
E0 e
e
vak
vak
n−t 
Amplitude
Die Amplitude nimmt mit exponentiell mit der Ausbreitung (wachsendes r) ab. 146
Die Absorption bewirkt also eine gedämpfte Schwingung.
Die Ursache der Dämpfung liegt in der Leitfähigkeit.
≠0


j= E

v=j⋅E.
Es fließt ein Strom bei bei der Frequenz der elektromagnetischen Welle. Der
Stromfluss ist immer mit Joule'scher Wärme verbunden.
Die Umwandlung von elektromagnetischer Energie in Wärme zeigt sich in der
exponentiell kleiner werdenden Amplitude der Schwingung.
Der Imaginärteil des komplexen Brechungsindex steht für die Absorption (kvakκ)
und kann als Absorptionskoeffizient α interpretiert werden.
(Im Allgemeinen ist der Absorptionskoeffizient = 2 kvakκ, da die Intensität
proportional zum Betrag des Poyntingvektors |S| ist.)
Wenn ein Material bestimmte Frequenzen absorbiert, ist es in diesem Bereich
immer leitfähig für einen Wechselstrom mit diesen Frequenzen.
z.B. Glasfilter: grünes Glas - absorbiert rotes Licht und ist in diesem
Frequenzbereich auch leitfähig.
147
Die Absorption ist also direkt mit dem komplexen Brechungindex verbunden. Dieser
kann auch direkt aus der Dielektrizitätskonstante abgeleitet werden. Damit wird
die elektromagnetische Wechselwirkung direkt mit einer Materialeigenschaft in
Beziehung gesetzt.
n =
 
 2 µ2r
1
r µr  2r µ2r  2 2
2
 0
für   0
n   r µr
 
 2 µ2r
1
2 2
 =
−r µr  r µr  2 2
2
 0
für   0
●
●
●
=0
Wurzel einer komplexen Zahl ist mehrdeutig, gewählt wird die Lösung für die
σ = 0 für ω -> 0 ist.
n(ω) heißt Dispersion, starke Abhängigkeit von σ(ω), ε(ω) und eventuell µr(ω).
148
Historisches: Warum eigentlich Telegrafengleichung?
Wilhelm Weber und Carl Friedrich Gauß führten 1833 Versuche mit einem
elektromagnetischen Telegrafen durch. Im selben Jahr gelang ihnen die erste
telegrafische Nachrichtenübertragung vom Physikgebäude in der Göttinger Innenstadt
zur Göttinger Sternwarte. Zur Nachrichtenübertragung dienen positive oder negative
Spannungspulse, die durch gezieltes Umpolen und Auf- und Abbewegen einer
Induktionsspule erzeugt werden. Der entscheidende Durchbruch kam 1837 mit dem von
Samuel Morse konstruierten und 1844 verbesserten Schreibtelegrafen.
Mit der Verlegung von Seekabeln wurde 1839 begonnen. Nach mehreren Fehlschlägen
wurde die erste Verbindung zwischen Europa und Nordamerika 1857/58 eingerichtet.
Johann Carl Friedrich Gauß
Wilhelm Weber
24. Oktober 1804 in Wittenberg 30. April 1777 in Braunschweig
† 23. Februar 1855 in Göttingen
† 23. Juni 1891 in Göttingen
Samuel Finley Breese Morse
27. April 1791 in Charlestown
† 2. April 1872 in New York
149
5.7. Strahlung eines schwingenden Dipoles
Ebene Wellen kommen aus ∞ und gehen nach ∞.
Was ist ihre Ursache? Wie enstehen elektromagnetische Wellen?
Es sind Quellen notwendig: Antenne, Lichtquelle
Für Quellen gilt: ̇≠0 wegen ̇div j=0

j≠0
Die Quelle soll sich in Koordinatenursprung bei r = 0 befinden.
Außerdem soll wie bisher gelten:
 = ̇
rot H
E
 =0
div H
 =−µ ̇
rot E
H
 =0
div E
Damit gilt die Wellengleichung
ohne Absorption.
 und H

Hertz hat einen Trick gefunden, wie man eine Lösung für E
findet, um dann auf ̇ und j
im Ursprung zurück zuschließen
(Insofern genial, da andere Wege meist nur auf die Fernfelder weit weg von
der Antenne kommen.)
150
Hertzscher Hilfsvektor Z :
r ≠0 :
 =rot ̇
H
Z
Heinrich Rudolf Hertz
22. Februar 1857 in Hamburg
† 1. Januar 1894 in Bonn
rot rot ̇
Z = ̇
E
1
  zeitlich konstantes Feld

E = rot rot Z

Annahme: für eine ungeladene Antenne (ρ = 0) sei das zeitlich
konstantes Feld ≡ 0
 = 1 rot rot Z
 = 1 [grad div Z
 − 
E
Z]


Aus den Maxwellschen Gleichungen und dem Hertzschen Hilfsvektor erhalten wir
̇ = − rot ̈
rot 
E = − H
Z = rot −µ ̈
Z grad 
 =−µ ̈
E
Z grad 
mit beliebigem φ, da rot grad φ ≡ 0.
1
1
grad div Z −  Z =− ̈
Z grad 


151
nun wird φ so gewählt, dass gilt
1
grad div Z =grad 

1
 = µ ̈
Z
Z = 2 ̈
Z
c
Man löse nun diese Gleichung für Z und berechne H und E aus
1
 =−µ ̈

E
Z  grad div Z

 =rot ̇
H
Z
Eine Lösung wäre natürlich:
 = Z0 e i k⋅r −t ,
Z
aber diese Lösung erlaubt keinen Rückschluss auf j in der Quelle.
 r ,t = Z0 e
Z
Kugelwellen als Ansatz von Hertz:
i  t−k r 
r
Kugelwellen sind Lösung, falls ω = ck. Die Amplitude von Z (nicht E oder H) ist
konstant, falls
 t=k r

r 
= =c
t
k
Die Amplitude ist konstant auf einer Kugel, deren Radius mit Lichtgeschwindigkeit
152
wächst.
Beweis: In Kugelkoordinaten gilt:
2
∂
2
= 2  ∂ Winkelableitungen
∂r r ∂r
Die Winkelableitungen spielen keine Rolle, da unser Ansatz Z nicht von
Winkeln abhängt.
 r ,t = Z0 e
Z
 
 
 
    [
∂ Z
 =− 1 Z
  1 −ik  Z 0 ei  t− kr =− 1 ik Z

∂r
r
r
r
2
1 1
∂ Z
= 1 
 ik  1 ik
Z

ik
Z
r r
r
∂r2
r2
2
1
1
2 1
  ik 
=
⇒
Z= 2 Z
Z−
ik Z
r
r r
r
Damit erhalten wir:
 
] 
i  t−k r 
r
2
= 1 Z
  1 ik 
Z
Z
2
r
r
1
2 1
1 
2
= 1 

ik −
ik Z
Z
ik

Z
−
Z =−k 2 Z
2
2
r
r r
r
r
2
 Z =−k Z
2
1 ̈ − 
Z= 2 Z
2
c
c
=
Z
1 ̈
Z ist erfüllt, falls =ck
2
c
153
Berechnung von H:
Es gilt:
 =rot ̇

H
Z =i  rot Z
 r ,t = Z0 e
Z
rot  V = rot V −V ×grad 
[
 = −i  Z0×grad 1 e i t −k r  = −i  Z0 × −r e i  t−kr  1 grad e i t −kr 
H
r
r
r3
Für den Term mit grad ei(ω t - k r) gilt:
r
]
r=  x 2  y 2 z 2
2
2
2
∂ e i t−k r =e i t−k r  −ik  ∂  x  y  z =−ik e it−k r  1
∂x
∂x
2
 grad e
i  t−k r 
i t−k r 
2x
−ik i t−k r 
=
e
x
2
2
2
 x y z r
~r
Damit erhalten wir für das Magnetfeld:
[
]
 =i 0 Z0 × r  i k r ei t −k r =i 0 Z0 × r i r r 2  e i  t−k r 
H
3
2
3
3
r
r
r
r 
[
]
Erstes Glied wichtig für r < λ: Nahfeld, Nahzone
Zweites Glied wichtig für r > λ: Fernfeld, Fernzone
154
1. Nahzone:
Um auf j in der Antenne zu schließen:
und nur erstes Glied für H:
r 0
e
−ikr
−i
=e
2
r

0
≈e ≈1
 =i  Z0 × r3 e i  t
H
r
wenn wir ein harmonisch veränderliches Z0 einführen
Z0 t = Z0 e i  t
r
 =i  Z0 t  × r = ̇
H
Z
t

×
0
r3
r3
Nahzone ist nicht nur r < λ, sondern auch ω -> 0, da =2 c / , d.h. wir suchen
eine Lösung für niederfrequente Wechselströme, die obiges H liefern.
Erinnerung: Biot-Savart: Drahtstück dr' bei r' = 0 erzeugt ein Magnetfeld bei r.
  r = I d r ' × r
dH
4
r3
(sieht überraschend ähnlich aus!)
155
Jetzt kommen wir endlich zu einem Dipol:
 Q
−Q
 d r '
mit Qt =Q 0 e
p =Q d r '
i t
i t
p t =Q d r ' =Q 0 e d r '
Ursache für zeitlich veränderliche Ladung in einem Volumen ist ein Strom der
fließt
Id r ' =Q̇ d r ' =̇p t
Unsere Lösung entspricht einer mit Wechselstrom gespeisten Dipolantenne, falls
̇pt 
p
̇
Z 0 t =
bzw. Z0=
4
4
Insgesamt gilt für das H-Feld:
 =i 
H
p0
r ik
r ik
i t −kr i 
× 3  2 r e
=
p0 ei t−kr × 3  2 r
4
4
r r
r r
p t = p0 e
[
it
p0 e
]
i t −kr 
  [
[
= p0 e
 = p t− kr = p t− r 
i  t−
kr


  [
c
 = i  p t− r × r  ik r = 1 ̇p t− r × r  ik r
H
3
2
3
2
c
c
4
4
r r
r r
]
]
]
156
2. Fernzone:

1
1
ik =i  ~ ∂
c ∂t c

nur zweites Glied
  r ,t = ik ̇pt− r  × r = 1 ̈pt− r  × r
H
c
c
4
r 2 4 c
r2
H(t) wird verursacht durch einen Strom zu einem früheren Zeitpunkt
Die Differenz zeigt Kausalität der Wellenausbreitung mit c.
Berechnung von E:
t−
r
c
1

̈
E=−µ
Z  grad div Z

p
Z = 0 1 e i  t−kr 
4 r
Als Übung für Ableitungen sehr zu empfehlen :-)
157
Als Lösung erhält man:
[
]
 =µ 2 Z
 − 1 p0 1  ik e i t−kr 
E
4 
r3 r2
1
r
r it−kr 
−
p
⋅
r
−3
−2
ik
e




0
3
4
4 
r
r
1
1 ik
ik r i t−kr 
−
p
⋅
r

−
e




0
3
2
4 
r
r r
[
[
]
]

Verschiedene Zonen:
d= Größe der Quelle
2
Fernzone:
Mittelzone:
Nahzone:
(für H war die Nahzone ~
2
 
2 1
k
1
~
~
r
r
 r
k 2
1
~
~
r 2 r 2
r2
1
~ 3
r
d ≪≪r
d ≪r~
d ≪r≪
1
1
~
und
Fernzone
)
2
r
r
158
Im folgenden Teil wird nur die Fernzone diskutiert (Nah- und Mittelzone sind
allerdings wichtig für Geophysik oder Nahfeldmikroskopie)
1  p0⋅r  r 2 i  t−kr 
2


E  r ,t =µ  Z −
k e
3
4  r
mit
2
2 
2
k = 2 =  µ
c
p0 e i t−kr
Z =
4 r
2

µ i t−kr  p0  r⋅r   p0⋅r  r

E r ,t =
e
−
3
3
4
r
r
[
Es gilt:
]
r × p0×r = p0 r⋅r −r r⋅
p 0
2
µ
1
  r , t=
E
e i t−kr  3 [ r × p0 ×r  ]
4
r
159
Wie früher gilt:
r
i t− 
r
it−kr 
c
p t = p0 e  p t− = p0 e
= p0 e
c
r
r
2
̈pt− =− p t− 
c
c
it 
Als Ergebnis für die Fernzone erhalten wir:


 r ,t = 1 ̈p t − r  × r
H
4 c
c
r2
  r , t=  1 r × r × ̈p t− r 
E
4 r3
c


Für elektromagnetische Wellen haben wir bereits einen Zusammenhang zwischen E
und H hergeleitet.

E r ,t =µc H ×r =µc H
 ×e
r
160
Nachfeld wird beeinflusst durch Ladungen und Ströme der Quelle. Die
elektrischen Feldlinien bei der Quelle folgen den Schwingungen der Ladungen.
i t
p t = p0 e
161
Das Fernfeld wird nur durch die gegenseitige Induktion bestimmt.
162
163
Winkelbeziehungen:
E =0
r⋅
 =0
r⋅H
⋅H
 =0
E
}
stehen senkrecht aufeinander
Für den Poynting-Vektor folgt:
 
 1 r
r

S=
̈
p
t−
×r ]
[
c 16  r
c
A× 
 = 
 − C
  A⋅B

B ×C
B  A⋅C

S= E
 ×H
 =  c H ×r × H
 =  c H⋅
 H
 r
r
r
2
5
2
∣
S∣~

r
4
2
2
sin 
̈p
Die Energie verteilt sich auf immer größere Kugelflächen, die sich mit
Lichtgeschwindigkeit ausbreiten.
164
Zusammenfassung
●
Elektromagnetische Wellen können durch eine Dipolantenne
(schwingendes Ionenpaar = schwingender Dipol) erzeugt werden.
●
Die elektromagnetischen Felder nehmen für große Entfernungen mit 1/r ab.
●
Die Ausbreitung der Wellen erfolgt mit Lichtgeschwindigkeit.
●
Längs der Dipolachse findet keine Abstrahlung ab, Maximum der Abstrahlung ist
senkrecht zum Dipolmoment.
H-Feld: Dipolmoment entlang der z-Achse, θ sei Winkel zur z-Achse
- konzentrische Kreise um den Dipol
- |H| wird mit sinθ schwächer (Null für θ=0,π)
●
E-Feld: tangential zu den Längenkreisen
- Für θ=0,π ist E in der Fernzone Null, d.h. die Terme der Nah- und Mittelzone
werden wichtig. Diese Terme sind die Ursache für das Abbiegen der elektrischen
Feldlinien.
●
Magnetfelder sind mit den Wirbeln der elektrischen Felder und umgekehrt verknüpft.
http://www.mikomma.de/fh/eldy/hertz.html
165
Zusammenfassung
●
Eine Dipolantenne empfängt das elektrische Feld, Sender und Empfänger sollten
parallel zueinander stehen,
Das Magnetfeld kann über das Faraday'sche Induktionsgesetz genutzt werden
(Ferritantenne, durch viele Wicklungen um einen Ferritkern kann die induzierte
Spannung vergrößert werden.)
Da die elektrische und magnetische Energiedichte gleich ist, sind diese Antennen
gleichwertig.
●
Der Poyntingvektor gibt die Energieabstrahlcharakteristik. Die Energie verteil sich
auf immer größere Kugelflächen, die sich mit c ausbreiten.
4 2
∣s∣~ 2 sin 
r
Die Frequenzabhängigkeit in der 4. Potenz ist Ursache für die historische
Entwicklung Langwelle -> Mittelwelle -> Kurzwelle -> UKW.
166
Jede beschleunigte Ladung strahlt elektromagnetische Wellen ab.
Id r ' =Q̇ d r ' =̇p t
Für eine Punktladung ρ=qδ(r-r0) ergibt sich:
I d r =∫ j⋅d f d r =∫  v⋅d V =∫ q  r −r0  
v⋅d V =q 
v =̇p t
̈pt  = q ̇v
Anwendungen/Bedeutung:
●
●
●
●
●
Atommodell
Röntgenbremsstrahlung
Synchrotronstrahlung = sehr breites,
kontinuierliches Spektrum vom infraroten über den
sichtbaren Spektralbereich, ins ultraviolett bis tief
in den Bereich der Röntgenstrahlung mit hoher
Strahlungsintensität
167
●
●
Freier-Elektronen-Laser (einer von 21 weltweit in 2006 ist in Rossendorf bei
Dresden)
Rayleigh-Streuung ist die Streuung elektromagnetischer Wellen an Teilchen, die
klein im Vergleich zur Wellenlänge λ der Wellen sind. Der Streuquerschnitt ist
proportional zur vierten Potenz der Frequenz.
Blaues Licht wird stärker gestreut als rotes. Dieser Effekt ist für die blaue Farbe
des Himmels bei hohem Sonnenstand, sowie für die rote Farbe bei Sonnenaufgang
und Sonnenuntergang verantwortlich.
168