Mittwoch, 23. November 2011 Torsten Wittmaack Thema

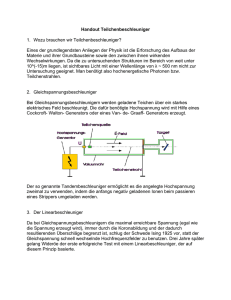
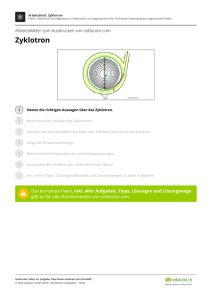
Mittwoch, 23. November 2011 Torsten Wittmaack
Thema: Welche Aufgabentypen können in der Klausur vorkommen?
Vergleichsaufgabe: klassische Rechnung
relativistische Rechnung
Bsp.
Linearbeschleuniger
Zyklotron
Synchrotron
1) Wie groß darf ein Zyklotron sein, damit man nicht relativistisch rechnen muss?
r
U
Im Zyklotron wirken die Zentripetalkraft
m v2
Fz =
r
und die Lorentzkraft.
Fl = q v B
Gleichsetzen der Kräfte führt zu:
Fz = F l
m⋅v 2
=q⋅v⋅B
r
B
mv
=q⋅B
r
m⋅ω=q⋅B
q
ω= ⋅B
m
Ausrechnen der
Winkelgeschwindigkeit
v=ω⋅r
(die Zyklotronfrequenz)
q B
f= ⋅
m 2⋅π
Um nun zum größten Radius zu gelangen bei dem man nicht relativistisch
v
rechnen muss, setzt man für Omega ω=
ein und erhält folgende
r
Gleichung die man nach r auflöst.
v q
= ⋅B
r m
r
m
=
v q⋅B
v⋅m
r=
q⋅B
Da man ab einer Geschwindigkeit von
1
⋅c relativistisch rechnen muss,
10
1
⋅c ein und erhält für den maximalen
10
Radius: r = m⋅0,1 c
max
q⋅B
setzt man für v =
2)
Wenn die Teilchen sehr hohe Geschwindigkeiten erreichen, muss man relativistische Effekte
berücksichtigen. Diese führen dazu, dass Teilchen mit einem Zyklotron obiger
Bauart nur auf eine bestimmte maximale
Energie beschleunigt werden können, weil sie, wie man sagt, „aus dem Takt“ geraten.
Erklären Sie, welcher relativistische Effekt in diesem Fall eine entscheidende Rolle
spielt. Erläutern Sie qualitativ, warum die Teilchen „aus dem Takt“ geraten und daher
nur auf eine bestimmte maximale Energie beschleunigt werden können.
Lösung:
Mit wachsender Geschwindigkeit muss man die dynamische, also die mit der Geschwindigkeit
anwachsende Masse berücksichtigen.
π⋅m
Gemäß t D =
ist die Dauer eines Umlaufs dann nicht mehr konstant, sondern
q⋅B
wächst mit zunehmender Masse. Die Umlaufdauer passt nicht mehr zu der nach klassischer
Berechnung ermittelten Frequenz der Beschleunigungsspannung. Die Teilchen erreichen
den Spalt nicht mehr zu dem für eine optimale Beschleunigung günstigsten Zeitpunkt,
sondern sie kommen verspätet an.
Sie werden daher weniger beschleunigt bzw. werden gebremst, wenn sie bei umgekehrter
Polung der Wechselspannung den Spalt erreichen. Also gibt es ein Maximum der
Energie der Teilchen.
3)
Elektronen können mit einem Zyklotron der bisher behandelten Bauart nur auf relativ
kleine Energien beschleunigt werden. Daher wurde eine Modifikation entwickelt, die
zum so genannten Elektronenzyklotron führte.
Dabei wird zur Beschleunigung von Elektronen der Scheitelwert der angelegten Wechselspannung
auf genau 511 kV eingestellt.
Zeigen Sie, dass die kinetische Energie eines Elektrons bei jedem Durchqueren des
Spalts um die Ruheenergie zunimmt.
Man kann die Masse nach dem n-ten Umlauf durch die Beziehung m = m0 · (2 · n +1)
ausdrücken, d. h., die Umlaufzeit wächst bei jedem Umlauf gemäß der in Teilaufgabe 2)
angegebenen Beziehung.
Begründen Sie, warum die Frequenz (bzw. Periodendauer) der Wechselspannung trotzdem
konstant gewählt werden kann.
Lösung:
Gemäß der Beziehung E = m⋅ c² entspricht eine Energie von 511 keV der Masse
511⋅103 V⋅1,602⋅10−19 C
m=
=9,11⋅10−31 kg
2
m
( 2,997⋅108 )
s
Dies ist der Literaturwert für die Ruhemasse eines Elektrons.
Die Umlaufdauer wachst bei jedem Umlauf um ein ganzzahliges Vielfaches der Periodendauer
der gewählten Beschleunigungsspannung, d. h., die Teilchen erreichen den Spalt um
die entsprechende Anzahl von Perioden später, es ergibt sich aber keine Phasenverschiebung.
Weitere mögliche Aufgaben sind:
4) Notieren der Grundprinzipien der Relativitätstheorie (s. Buch S. 345)
5) Notieren der Formeln zu Zeitdilatation u. Längenkontraktion (s. Buch S. 348/349 u. S. 352)
6) Herleiten der Formel zur Geschwindigkeitsaddition (s. Buch S. 357)
7) Aufgaben zum optischen Doppler-Effekt (wird noch behandelt s. Buch S. 358)
8) Diskutieren des Begriffs der Gleichzeitigkeit ( s. Buch S. 346)
9) Das Hafele Keating Experiment (s. "Übungsblatt zu Hafele Keating“ Buch S. 351)
10) Myonen Experiment (aus Sicht der Myons und aus Sicht eines auf der Erde befindlichen
Menschen s. Buch S. 350/352)
11) Zwillingsparadoxon
12) Aufgaben zur Längenkontraktion (s. AB "Das Schuppenparadoxon" u. Buch S. 352)