Zeitabhängige Felder, Maxwell

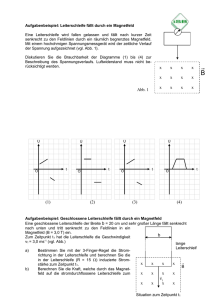
Zeitabhängige Felder,
Maxwell-Gleichungen
Man beobachtet, dass ein zeitabhängiges Magnetfeld ein elektrisches
Feld erzeugt. Dies führt z.B. zu einer Spannung an einer Drahtschleife
(Induktion).
Umgekehrt beobachtet man auch: ein zeitabhängiges elektrisches Feld
erzeugt ein Magnetfeld.
Auf diese Weise werden elektrische und magnetische Felder gekoppelt.
Die Kopplung über die Zeitabhängigkeit ermöglicht elektromagnetische
Wellen.
In den Maxwell-Gleichungen werden diese Zusammenhänge
mathematisch formuliert.
150
Induktion
Ein zeitabhängiges Magnetfeld erzeugt ein elektrisches Feld.
Elektrische Felder lassen sich besonders gut an einem Leiter messen,
an dem sie eine Spannung erzeugen wegen der wiederum ein Strom fließt.
Auf diese Weise steht Leistung P=U·I für den Messprozess zur Verfügung.
Wir beobachten daher diesen Effekt besonders gut an Leiterschleifen, an
denen durch ein zeitabhängiges Magnetfeld eine Spannung induziert wird.
r
∂B
∂t
r
E
U ind
151
In der Elektrostatik waren elektrische Felder immer wirbelfrei.
Bei der Induktion wird dagegen ein wirbelförmiges elektrisches Feld
erzeugt, das entlang der Leiterschleife verläuft.
Integriert man entlang der Leiterschleife ergibt sich eine Spannung Uind
an den offenen Enden:
U ind
r r
= ∫ E ⋅ ds
Leiter −
schleife
M. Faraday fand 1831 folgenden Zusammenhang:
Die Spannung ist proportional zur umschlossenen Fläche der Leiterschleife.
proportional zur zeitlichen Änderung des Magnetfeldes.
proportional zum cos des Winkels zwischen B und
U ind = −
r r
∫ B ⋅ dA
d
dt Leiter −
der Flächennormalen
schleife
152
Mit dem magnetischen Fluss Φ durch die Fläche der Leiterschleife
r r
Φ = ∫ B ⋅ dA
lässt sich einfach formulieren:
U ind
dΦ
=−
dt
Faradaysches Induktionsgesetz
Eine Spannung wird induziert, wenn sich die magnetische Feldstärke ändert,
oder wenn sich die Fläche der Leiterschleife ändert, oder wenn die
Orientierung der Leiterschleife zum Feld sich ändert.
Experimente:
Annähern eines Magneten an eine Leiterschleife
Vergrößern einer Leiterschleife
Drehen einer Leiterschleife im Magnetfeld
153
An einer Spule mit n Windungen ist die relevante Fläche n mal die
Querschnittsfläche A der Spule:
r
A
r
∂B
∂t
U ind
Die an einer Spule induzierte Spannung ist proportional zur Fläche und
zur Anzahl der Windungen der Spule.
Ändert sich das Magnetfeld sehr schnell, können an einer Spule u.U.
sehr hohe Spannungen induziert werden.
Beispiel: schnelle Änderung der magnetischen Feldstärke eines
Elektromagneten bei dem der Strom ein- bzw. ausgeschaltet wird.
154
Lenzsche Regel:
Durch die induzierte Spannung und den in der Leiterschleife fließenden
Strom wird Feldenergie in Wärmeenergie umgewandelt.
Diese Energie muss an anderer Stelle als Arbeit aufgewendet werden.
Der induzierte Strom erzeugt wiederum ein Magnetfeld, dass dem
ursprünglichen Magnetfeld entgegengerichtet ist. Dadurch wird Arbeit beim
Bewegen eines Magneten in der Leiterschleife verrichtet.
155
Wirbelströme:
Induktionsströme, die in einem ausgedehnten Leiter (z.B. Metallplatte)
erzeugt werden, nennt man Wirbelströme.
Wirbelströme können technisch für Bremsen ausgenutzt werden.
Die Bremskraft ist proportional zur Geschwindigkeit, was ein weiches
Bremsen ermöglicht. Die Bremskraft kann elektrisch über einen
Elektromagneten gesteuert werden.
Früher wurden Wirbelströme bei mechanischen Tachometern ausgenutzt.
156
Selbstinduktion:
Ändert man den Strom, der durch eine Spule fließt, ändert sich das
Magnetfeld, das die Spule erzeugt. Diese Änderung induziert an der Spule
eine Spannung und damit einen Strom, der dem ursprünglichen Strom
entgegengerichtet ist.
Der Strom I in der Spule erzeugt ein Magnetfeld mit der Feldstärke B
und den magnetischen Fluss in der Spule:
r r
Φ = ∫ B ⋅ dA
B ist proportional zum Strom also ist auch Φ proportional zum Strom.
Φ=LI
Die Proportionalitätskonstante L nennt man Induktivität der Spule.
Sie hängt von der Geometrie, der Windungszahl und der Permeabilität μ
des Spulenkerns ab.
157
Einheit der Induktivität ist das Henry [H]
Vs
1H =1
A
Die durch Selbstinduktion an der Spule induzierte Spannung ist:
U ind = −
dΦ
d( LI )
dI
=−
= −L
dt
dt
dt
U ind = − L
dI
dt
Selbstinduktion
158
Einschaltvorgang:
Schaltet man den Strom in einem Stromkreis mit Spule ein,
dann steigt anfänglich die Stromstärke mit der Steigung
U
dI
=− 0
dt
L
an, so dass die induzierte Spannung gerade die gesamte anliegende
Spannung aufhebt.
Fließt dann ein Strom, fällt auch an dem ohmschen Widerstand der Spule
Spannung ab und der Strom erreicht den Wert I = U / R.
I
I=
U0
+
I
U0
R
dI
U
=− 0
dt
L
t
159
Der genaue Kurvenverlauf ergibt sich aus:
U 0 = I R − U ind = I R + L
dI
dt
Die Differentialgleichung hat als Lösung eine Exponentialfunktion der Form
I (t ) = I 0 + I1 e − t /τ
Einsetzen des Ansatzes ergibt
U 0 = I 0 R + I1 R e − t / τ − I1
L
τ
e −t / τ
Es folgt für die Parameter und aus der Anfangsbedingung I(0) = 0 :
U0
I0 =
R
und
L
τ=
R
und
I1 = − I 0
Die Lösung lautet also
R
− t⎞
U0 ⎛
⎜1 − e L ⎟
I (t ) =
⎟
R ⎜⎝
⎠
160
Abschaltvorgang:
Schaltet man den Strom aus, klinkt der Strom durch die Spule nicht abrupt
auf null ab, sondern es fließt durch Selbstinduktion ein Strom über den
Widerstand R0.
I
R0
U
L, RL
I=
U0
RL
+
I
t
Nach Öffnen des Schalters gilt entsprechend der Maschenregel:
I ( R0 + RL ) − U ind = 0
I ( R0 + RL ) + L
dI
=0
dt
161
Die Differentialgleichung hat die Lösung
I (t ) = I 0 e
−
R0 + RL
t
L
und aus der Anfangsbedingung
U0 −
I (t ) =
e
RL
I (0) = U 0 / RL folgt
R0 + RL
t
L
Am Widerstand R0 fällt die Spannung U ab:
−
R0
U (t ) =
U0 e
RL
R0 + RL
t
L
Bei t=0 hat man eine um den Faktor R0/RL höhere Spannung als U0
Technische Anwendungen findet man bei der Zündspule im Auto,
dem Weidezaun, Zündung von Leuchtstoffröhren, etc.
Die Hochspannung ist oft ungefährlich, da nur sehr kurzzeitig ein Strom
fließen kann und die Gesamtenergie des Strompulses klein ist.
162
Induktivität einer Zylinderspule
Das Magnetfeld in einer Zylinderspule der Länge l mit n Windungen ist
(siehe Seite 103):
B = μ0
n
I
l
Der magnetische Fluss durch n-mal die Querschnittsfläche A ist
A n2
Φ = μ0
I
l
A n2
Die Induktivität der Spule ist somit: L = μ 0
l
und die durch die Selbstinduktion induzierte Spannung:
U ind
A n 2 dI
= −μ0
l dt
163
Energie des Magnetfeldes
Zum Aufbau des Magnetfeldes in einer Spule wird Energie benötigt.
Diese wird von der Spannungsquelle beim Einschalten als Arbeit geleistet,
wenn ein Strom gegen die induzierte Spannung fließt.
Für den Stromkreis gilt
U 0 = I R − U ind
Multipliziert man mit
dI
= I R+L
dt
U0
+
-
I erhält man
I
PBatterie = U 0 I = I 2 R + L I
dI
= PWärme im + PMagnetfeld
dt
Widerstand
Integriert man mit I(t) über die Zeit erhält man die Gesamtenergie des
Magnetfeldes:
∞
dI
W = ∫ L I dt =
dt
0
I max
∫
0
1 2
L I dI = L I max
2
164
Energiedichte des Magnetfeldes
Fließt in einer Zylinderspule mit Induktivität L der Strom I, dann ist die
Gesamtenergie des Magnetfeldes
W = 12 L I 2
In der Spule herrscht die Magnetfeldstärke
B = μ0
A n2
Die Induktivität der Spule ist L = μ 0
l
n
I
l
Wir können die Gesamtenergie also schreiben als
2
1 2 1
A n2 2 1 1
n
1 1
W = L I = μ0
I =
Al μ 02 2 I 2 =
V B2
2
2
l
2 μ0
l
2 μ0
Unter der Annahme, das das Feld im Außenraum sehr schwach ist erhält
man daraus die Energiedichte des Magnetfeldes:
W 1 1 2
w=
B
=
V 2 μ0
(vgl. Seite 110b)
165
Verschiebungsstrom
Ein zeitabhängiges elektrisches Feld erzeugt ein Magnetfeld.
Ist eine Leiterschleife durch einen Kondensator unterbrochen und fließt ein
Strom I, dann läd sich der Kondensator auf
U = Q/C = I t /C
Das elektrische Feld im Kondensator wächst linear mit der Zeit an E =
It
dC
Um dieses zeitabhängige elektrische Feld herum wird ein wirbelförmiges
r
B
Magnetfeld erzeugt.
r
B
r
∂E
∂t
r
B
I
Das zeitabhängige elektrische Feld wirkt wie ein Strom. Daher nennet man
es Verschiebungsstrom.
166
r
∂E
Ein zeitabhängiges Feld
am Ort r wirkt wie eine Stromdichte jV an
∂t
diesem Ort
r
r
∂E
jV = ε 0
∂t
Verschiebungsstromdichte
Für den Plattenkondensator leitet man diese Beziehung einfach her:
E=
It
dC
⇒
r
∂E
I
I 1 d 1 I
1
=
=
=
=
j
∂t d C d ε 0 A ε 0 A ε 0
Die Magnetfeld erzeugende Wirkung von Strömen und Verschiebungsströmen ist gleich.
Nur die zeitliche Änderung eines elektrischen Feldes erzeugt ein Magnetfeld.
Statische elektrische Felder im Kondensator haben kein Magnetfeld um sich.
167
In der Elektrostatik und Magnetostatik hatten wir vier Gleichungen, die
die Erzeugung von elektrischen und magnetischen Feldern beschreiben:
r
rot E = 0
Elektrische Felder sind wirbelfrei
r
r
rot B = μ 0 j
Amperesches Gesetz
r ρ
div E =
Poisson-Gleichung
r
div B = 0
Quellenfreiheit des Magnetfeldes
ε0
Bei zeitabhängigen Feldern kommen zwei zusätzliche Erzeugungsmechanismen hinzu: die Induktion und der Verschiebungsstrom
U ind
dΦ
=−
dt
r
r
∂E
jV = ε 0
∂t
168
Maxwell-Gleichungen
Fügt man diese Mechanismen in die Gleichungen ein erhält man:
r
r
∂B
rot E = −
∂t
r
r
r
∂E
rot B = μ 0 j + μ 0ε 0
∂t
r ρ
div E =
Maxwell-Gleichungen
ε0
r
div B = 0
Dieses gekoppelte System von partiellen Differentialgleichungen beschreibt
die zeitliche Entwicklung von elektromagnetischen Feldern im Raum.
Die Maxwell-Gleichungen gehören zu den grundlegendsten und wichtigsten
Gleichungen in der Physik.
169
Maxwell-Gleichungen in Koordinatenschreibweise
∂E z ∂E y
∂B
−
=− x
∂y
∂z
∂t
∂B y
∂E x ∂E z
−
=−
∂z
∂x
∂t
∂E y ∂E x
∂B
−
=− z
∂x
∂y
∂t
∂E
∂Bz ∂B y
−
= μ 0 j x + μ 0ε 0 x
∂y
∂z
∂t
∂E y
∂Bx ∂Bz
−
= μ 0 j y + μ 0ε 0
∂x
∂z
∂t
∂B y
∂x
−
r
r
∂B
rot E = −
∂t
r
r
r
∂E
rot B = μ 0 j + μ 0ε 0
∂t
∂Bx
∂E
= μ 0 j z + μ 0ε 0 z
∂y
∂t
∂E x ∂E y ∂E z ρ
+
+
=
∂x
∂y
∂z ε 0
r ρ
div E =
∂Bx ∂B y ∂Bz
+
+
=0
∂x
∂y
∂z
r
div B = 0
ε0
170
Maxwell-Gleichungen in Materie
Befindet sich Materie im Raum, können die Maxwell-Gleichungen mit Hilfe
der Größen H und D ebenso einfach formuliert werden:
r
r
∂B
rot E = −
∂t r
r r ∂D
rot H = j +
∂t
r
div D = ρ
Maxwell-Gleichungen
in Materie
r
div B = 0
Hierbei sind auch die Konstanten μ0 und ε0 in D und H enthalten
r
r
D = ε ε0 E
r
r
B = μμ 0 H
Diese Form kann auch im Vakuum mit μ =1 und ε =1 verwendet werden.
171
Die außerordentlich große Komplexität elektromagnetischer Phänomene
wird deutlich, wenn man nicht nur die Felder und Polarisation von Materie
betrachtet, sondern zusätzlich die enge Kopplung an die Bewegung freier
Ladungen hinzunimmt.
Die Maxwellgleichungen zusammen mit der Lorenzkraft auf Ladungen
(
r r r
r
F = q E+v×B
)
und deren Beschleunigung gemäß den Newtonschen Axiomen
r
r
F = ma
liefert einen umfassenden Satz an Gleichungen der die klassische
Elektrodynamik vollständig beschreibt.
Eine Lösung dieser Gleichungen erfordert sehr hohen numerischen
Aufwand und ist für komplexe Probleme auch heute oft nicht möglich.
Zusätzlich werden in vielen Fällen relativistische Effekte relevant,
die in diesen Gleichungen nicht enthalten sind.
172