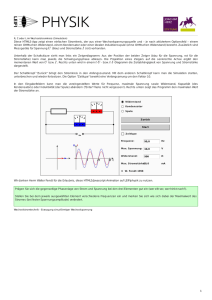
Elektromagnetische Induktion

Protokoll der Physikstunde vom 26.02.2004
Fabian Wartzek
Krefeld, den 29.11.04
Induktion
(Elektromagnetische Induktion)
1. Teil:
Versuch:
Wir haben eine Spule mit 1200 Wdg. an ein Voltmeter
angeschlossen. Die Empfindlichkeit betrug 100 mV. Dann haben wir
einen Hufeisenmagneten in die Spule eingeführt. Zur besseren
Anschaulichkeit haben wir anschließend den Nullpunkt in die Mitte der
Skala gelegt.
Beobachtung: Beim Bewegen des Magneten schlug das Voltmeter aus.
Nordpol rein à Ausschlag ins Negative
raus à Ausschlag ins Positive
Südpol rein à Ausschlag ins Positive
raus à Ausschlag ins Negative
Der Ausschlag betrug jeweils ca. 20 mV
Wir stellten fest das je ruckartiger (schneller) man den Magneten
bewegte, desto stärker war der Ausschlag. Folglich gab es keinen
Ausschlag, wenn man den Magneten nicht bewegte.
Es war ebenfalls egal, ob man den Magneten bewegte oder die
Spule.
2. Teil:
Versuch:
Wir haben statt des Hufeisenmagneten der 1. Spule eine gleich große
2. Spule gegenüber gesetzt, die über einen Schalter an und aus zu
schalten und an einen Trafo angeschlossen war.
Zuerst führten wir den Versuch ohne einen Eisenkern in der 2. Spule
durch.
Beobachtung: Ohne Eisenkern betrug der Ausschlag nur ca. 5 mV. Beim
Einschalten ins Positive und beim Ausschalten ins Negative.
Mit Eisenkern gab es beim Einschalten einen Vollausschlag ins
Negative (min. 50 mV). Der Ausschlag beim Ausschalten ins
Positive war ein wenig schwächer.
Protokoll der Physikstunde vom 26.02.2004
Fabian Wartzek
Krefeld, den 29.11.04
Erklärung:
Im folgenden wird vs als Geschwindigkeit des Leiters senkrecht zum magnetischen
Feld B verwendet. e ist die Elementarladung eines Elektrons. As die
Querschnittsfläche senkrecht zu B. n ist die Anzahl der Windungen der Spule.
Wie wir bereits bei den Versuchen festgestellt hatten, brachte immer eine
Veränderung des B-Feldes den Ausschlag. Beim 1. Versuch durch die Bewegung
des Magneten, beim 2. Versuch durch das Ein- und Ausschalten des Magneten.
Nun gibt es in der Literatur zwei Ansätze das Phänomen der Induktion zu erklären.
Der erste benutzt als Erklärung die Lorentzkraft. Hierbei wird angenommen, dass die
Elektronen eine Kraft (die Lorentzkraft) erfahren, die sie dazu bringt sich zu
verlagern. Dadurch entsteht ein elektrisches Feld, das dieser Kraft entgegenwirkt.
Dies ist ähnlich der Erklärung für die Hall-Spannung. Gilt aber nur, wenn ich einen
Leiter senkrecht zu den B-Feldlinien bewege.
Es ergibt sich hier nach folgende Formel:
FL = B * e * v s
Fel = e * E
B * e * vs = e * E
Da B an jeder Stelle konstant ist, muss auch E an jeder Stelle konstant sein.
Also gilt:
U ind = E * d
Aus:
B * vs = E
folgt:
U ind = B * d * v s
(d= Länge des Leiterstücks)
Die Deduktion der Formel für die Flächenänderung erspare ich mir an dieser Stelle,
da sie den Rahmen des Stundenprotokolls endgültig sprengen würde. Zu finden ist
sie auf den Seiten 57 und 58 unseres Physikbuches (Dorn Bader Physik 12/13).
Sie lautet:
∆A
U ind = n * B * s
∆t
Wenn nun andere Versuche betrachtet werden gerät die Erklärung mit Hilfe der
Lorentzkraft an ihre Grenzen. Bereits unseren zweiten Versuch kann sie nicht
erklären. Hier spielt anscheinend die Änderung der magnetischen Flussdichte B eine
Rolle.
Experimentell nachgewiesen ergibt sich folgender Zusammenhang:
∆B
U ind ~ n * As *
∆t
Es folgt also, dass in einer Spule mit n Windungen, welche in einem sich zeitlich
ändernden Magnetfeld B befindet (As = const.), eine Spannung induziert wird, die wie
folgt berechnet wird:
∆B
U ind (t ) = n * As *
∆t
Somit haben wir nun zwei Ursachen für die Induktionsspannung kennen gelernt. 1.
Die Änderung der Fläche und 2. die Änderung der magnetischen Flussdichte.
Protokoll der Physikstunde vom 26.02.2004
Fabian Wartzek
Krefeld, den 29.11.04
Zu 1. ergibt sich für die momentane Induktionsspannung
•
∆A
U ind 1 (t ) = n * B * lim s = n * B * A s (t )
∆t →o ∆t
analog dazu erhalten wir für 2.:
•
U ind 2 (t ) = n * As * B(t )
Treten diese beiden Ursachen gleichzeitig auf, erhält man für die
Induktionsspannung:
•
•
•
•
U ind (t ) = U ind 1 (t ) + U ind 2 (t ) = n * B * A s (t ) + n * As * B (t ) = n * (( B (t ) * A s (t ) + As (t ) * B (t ))
Nach der Produktregel der Differentialrechnung:
•
U ind (t ) = n * ( B (t ) * As (t ))
Michael Faraday bezeichnete das Produkt B(t)*As(t) als „magnetischen Fluss“
Weil es für ihn als Maß dafür galt wie viele Feldlinien durch einen bestimmten
Querschnitt gehen. Faraday nahm damals fälschlicherweise an, dass man die
Feldlinien wie Seile zählen könne. Nach Faraday ist also die Änderung der Menge an
Feldlinien, die durch einen bestimmten Leiterquerschnitt gehen, für die
Induktionsspannung verantwortlich.
Die Definition des magnetischen Flusses ist also:
Φ = B (t ) * As (t )
Die Induktion kann man also nun durch die Änderung der magnetischen Flussdichte
erklären. Also entweder Durch die Änderung der Querschnittsfläche senkrecht zu B
oder durch Änderung des magnetischen Feldes.
∆Φ
U ind (t ) = n *
∆t
Unter Betrachtung das
ält man für die
Momentanspannung:
•
U ind (t ) = n * Φ (t )
Bei genauerer Betrachtung würde man feststellen, dass die Induktionsspannung so
gepolt ist das sie durch ihren Strom ihrer Ursache entgegenwirkt. Dies ist das
lenzsche Gesetz.