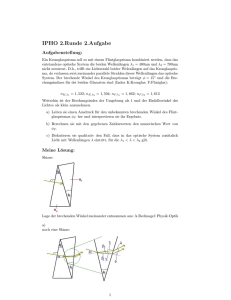
Nachklausur

PN2 Einführung in die Physik für Chemiker 2
SS 2016
Prof. J. Lipfert
Nachklausur
Name:
Matrikelnummer:
• Bitte schreiben Sie Ihren Namen auf jede Seite und legen Sie Ihren Lichtbildausweis bereit.
• Erlaubte Hilfsmittel: Taschenrechner, zwei beidseitig beschriebene DIN A4 Blätter, Wörterbuch
• Bearbeitungszeit: 120 min
• Ergebnisse bitte nur auf die Aufgabenblätter (ggf. auch die Rückseiten beschreiben).
• Viel Erfolg!
Aufgabe Erreichte Punkte Mögliche Punkte
1
30
2
15
3
20
4
20
5
15
⌃
100
Einige nützliche Konstanten
Erdmasse ME ⇡ 5.97 ⇥ 1024 kg
Erdradius RE ⇡ 6370 kg
Gravitationskonstante G ⇡ 6.67 ⇥ 10
11 m3
kg s2
C2
12
Dielektrizitätskonstante: ✏0 ⇡ 8.85 ⇥ 10
N m2
Magnetische Feldkonstante: µ0 ⇡ 1.26 ⇥ 10 6 TAm
Plancksches Wirkungsquantum (Planck-Konstante): h ⇡ 6.63 ⇥ 10
Elementarladung: e ⇡ 1.60 ⇥ 10 19 C
Masse eines Elektrons: me = 9.1 ⇥ 10 31 kg
1
34 J s
Name:
SS 2016
Aufgabe 1
Verständnisfragen (30 Punkte). Geben Sie kurze Antworten (1-2 Sätze, bzw. kurze Rechnung, bzw. einfache Skizze) auf die folgenden Fragen.
a) Ordnen Sie folgende Arten elektromagnetischer Strahlung nach Größe ihrer Frequenz (von
niedrigen zu hohen Frequenzen): i) Gammastrahlung aus dem Zerfall eines radioaktiven
Kerns, ii) Mikrowellen zum Erwärmen von Speisen, iii) rotes Licht aus einem Laserpointer,
iv) UV-Strahlung in einer Sonnenbank.
b) Sie haben jede Menge Widerstände mit R1 = 1.5 k⌦ und R2 = 3.0 k⌦ zur Verfügung,
benötigen aber einen Gesamtwiderstand von R = 2.0 k⌦. Skizzieren Sie eine Schaltung
mit der Sie dies erreichen und belegen Sie Ihre Wahl durch eine kurze Rechnung (Hinweis:
Rechnen Sie zunächst aus, welchen Widerstand eine Parallelschaltung von R1 und R2 hat).
c) In der Skizze fällt ein Strahl von links unten ein und tri↵t senkrecht auf die erste Grenzfläche
zwischen Luft und einem Glasprisma. Sie beobachten Totalreflektion an der zweiten Grenzfläche an der Oberkante des Prismas, unter einem Winkel ✓ = 45 . Was können Sie über
den Brechungsindex des Glases sagen?
2
Name:
SS 2016
d) Zeichnen Sie schematisch den Betrag des elektrische Feldes einer hohlen Metallkugel mit
Radius R und einer Gesamtladung Q als Funktion des Abstandes vom Mittelpunkt der Kugel
r , im Bereich r = 0...3R.
e) Eine Röntgenquelle mit Molybdän als Anodenmaterial emittiert Röntgenstrahlung mit einer
Photonenergie von 17.4 keV. Was ist die entsprechende Wellenlänge?
f) In den Skizzen eines Dipols (bestehend aus einer positiven und einer negativen Ladung)
unten, zeichnen Sie schematisch auf der linken Seite die Feldlinien und auf der rechten Seite
die Äquipotentiallinien ein.
3
Name:
SS 2016
g) Ein (als idealer Transformator genäherter) Schweißtransformator hat auf der Primärseite
N1 = 500 Windungen und wird mit 230 V Netzspannung betrieben. Die Sekundärspannung
soll bei 11,5 V liegen. Wie muss die Zahl der Windungen N2 auf der Sekundärseite gewählt
werden?
h) Wenn die Primärseite des Transformators aus der letzten Teilaufgabe mit einer I1,max = 10 A
Sicherung gesichert ist, wie viel Strom kann maximal auf der Sekundärseite fließen? Was sind
die Stromkosten, wenn der Schweißtransformator mit diesem maximalen Strom 2 Stunden
lang betrieben wird und wir einen Strompreis von 0,3 Euro pro Kilowattstunde annehmen?
i) Was ist die beugungslimitierte Auflösung eines Bildes rot ( = 600 nm) fluoreszierender
Moleküle in einem Mikroskop mit einer numerischen Apertur von N.A. = 1.4?
j) Mit welcher maximalen Genauigkeit lässt sich ein einzelnes der Moleküle aus der letzten Teilaufgabe lokalisieren, wenn insgesamt 10 000 Photonen von dem Molekül detektiert werden?
(Sie können davon ausgehen, dass die Detektionsgenauigkeit jedes einzelnen Photons dem
Beugungslimit entspricht.)
4
Name:
SS 2016
Lösung
a) Mikrowellen, roter Laser, UV Strahlen, Gammastrahlen
R2
b) Parallelschalten von R1 und R2 liefert R12 = RR11+R
= 1.0 k⌦. Reihenschaltung zweier
2
solcher Schaltungen liefert den gewünschten Gesamtwiderstand:
R1
R1
R2
R2
c) Es gilt nL = 1 (in seht guter Näherung) und für Totalreflektion sin ✓L = 1; somit
nG sin ✓G = nL = 1
Und damit:
nG =
p
1
= 2 ⇡ 1.4
sin ✓G
d) Feld ist innerhalb der Kugel, d.h. für r < R, Null, springt dann auf den Wert E =
Q/(4⇡✏0 R 2 ) und fällt dann / r12 ab.
e)
= hc/E = 0.71 Å = 7 ⇥ 10
11 m
f) Dipol: Siehe Vorlesung 2 Folie 9 und Vorlesung 2 Folie 19.
g) N2 = N1 · V2 /V1 = 500 · 11,5 V / 230 V = 25
h) Maximaler Strom: I2,max = I1,max · V1 /V2 = 10 A · 230 V / 11,5 V = 200 A;
Leistungsaufnahme ist P1 (= P2 ) = 230 V · 10 A = 2,3 kW; über einen Zeitraum von 2 h
werden 4,6 kW-Stunden verbraucht, die 1,38 Euro kosten.
i) Beugungslimit = Abbe-Limit gibt den kleinsten auflösbaren Abstand an (siehe Vorlesung 11,
Folie 18): d = 2N .A. = 600 nm / 2 / 1,4 ⇡ 214 nm.
p
j) Lokalisierung nach Detektion von N Photonen ist dSEM = pdN = 214 nm / 10000 = 2,14
nm (Siehe Vorlesung 12, Folie 11).
5
Name:
SS 2016
Aufgabe 2
Elektroskop (15 Punkte). Zwei sehr kleine Kugeln mit gleichen Massen m hängen an zwei
gleichlangen Drähten der Länge l . Beide Kugel werden elektrisch aufgeladen und tragen dann
die Ladungen q1 = q2 = q. Durch die Coulomb Wechselwirkung werden die Kugeln um eine
Strecke x bezüglich ihrer Ruhelage ausgelenkt.
a) Berechnen Sie die Ladung q der Kugeln indem Sie ein geeignetes Kräftegleichgewicht aufstellen. Vernachlässigen Sie die Gravitationskraft zwischen den Kugeln.
φ
l
x
b) Wie groß ist der Betrag der Ladung q der Kugeln für l = 10 cm, m = 5 g und x = 5 cm?
G
c) Stellen Sie das Verhältnis von Gravitationskraft zu Coulombkraft R = F
FC zwischen den
Kugeln auf. War es in Ordnung die Gravitationskraft in a) zu vernachlässigen?
6
Name:
SS 2016
Lösung
a) Auf die Kugeln wirkt die Gewichtskraft und die Coulombkraft. Wir zerlegen die Gewichtskraft
in eine Komponente senkrecht und parallel zum Draht, nur die senkrechte Komponente wirkt
rücktreibend auf die Kugel, die parallele Komponente wird ja vom Draht kompensiert.
FG,? = mg sin '
Entsprechend gilt für die Coulombkraft:
FC ,? = FC cos ' =
q2
4⇡✏0 (2x )2
cos '
Da sich im Gleichgewicht die senkrechten Komponenten genau kompensieren gilt:
r
⇣
⇣ x ⌘⌘
p
q = 4x ⇡✏0 mg tan ' = 4x ⇡✏0 mg tan arcsin
L
b) Einsetzen in das Ergebnis aus a):
q = 177.5 nC
c) Für das Verhältnis der beiden Kräfte gilt:
R=
FG
4⇡✏0 Gm 2
=
⇡ 6 ⇥ 10
FC
q2
12
Der Beitrag der Coulombkraft zum Kräftegleichgewicht ist also 11 Größenordnungen größer
als der der Gravitationskraft zwischen den Massen. Vernachlässigen völlig in Ordnung!
7
Name:
SS 2016
Aufgabe 3
Hall Sonde (20 Punkte). Eine Hall Sonde dient zur Bestimmung der Stärke eines Magnet~ gebracht. Es
feldes: Ein leitfähiger Quader mit Höhe b und Dicke d wird in ein Magnetfeld B
wird ein Strom I durch den Quader geschickt, was zu einer Ablenkung der Elektronen durch die
Lorentzkraft und damit zu einem Elektronenüberschuss auf einer Seite des Quaders führt. Dies
bewirkt ein elektrisches Feld und damit eine der Lorentzkraft entgegengesetzte elektrische Kraft,
die sich im Gleichgewicht genau kompensieren, sodass sich eine zur Stromrichtung senkrechte
Spannung UH , genannt Hall Spannung, ausbildet.
a) Stellen Sie das Kräftegleichgewicht aus Lorentz- und elektrischer Kraft auf und finden Sie
daraus einen Ausdruck für die Hall Spannung in Abhängigkeit der Geschwindigkeit der Elektronen v !
8
Name:
SS 2016
b) Verwenden Sie die Driftgeschwindigkeit v der Elektronen um zu zeigen, dass folgende Beziehung für die Hall Spannung gilt (wobei n die Dichte der freien Ladungsträger ist):
UH =
1 IB
ne d
c) Was ist die Dichte der freien Ladungsträger n, wenn sie mit einer d = 1 mm dicken HalbleiterHallsonde in einem homogenen Feld B = 0.1 T, bei einem Strom I = 1 A eine Hallspannung
UH = 1 V messen?
d) Nennen Sie mindestens drei unterschiedliche Mechanismen, wie man die Dichte freier Ladungsträger in einem Halbleiter erhöhen kann.
9
Name:
SS 2016
Lösung
a) Es muss gelten:
~ = e~v ⇥ B
~
eE
~ = B êz , die Elektronen fließen in x -Richtung (Strom in
Das B -Feld liege in z -Richtung, B
negativer x -Richtung!), dann gilt:
Ey = vB
Mit der Breite b des Quaders gilt:
UH
= vB
b
und damit:
UH = vbB
b) Die Driftgeschwindigkeit der Elektronen hängt mit der Stromdichte zusammen:
I
I
|~j | = en|~v | =
=
A
bd
Damit:
I
bden
Eingesetzt in den Ausdruck für die Hall Spannung:
v=
UH =
1 IB
en d
UH =
1 IB
en d
c) Die Hall Spannung ist gegeben durch:
damit gilt für die Dichte der freien Ladungsträger:
n=
1 IB
= 6.25 ⇥ 1020 1/m3
eUH d
d) Positive oder negative Dotierung; Erwärmen (sodass mehr freie Ladungsträger thermisch
aktiviert ins Leitungsband gelangen); Bestrahlen mit Licht / UV-Strahlung einer Wellenlänge,
die kurz genug ist, Elektronen über die Bandlücke aus dem Valenz- ins Leitungsband zu heben.
10
Name:
SS 2016
Aufgabe 4
Schwingkreis (20 Punkte). Für den abbgebildeten Schwingkreis gilt L = 580 H, C =
50 µF und U0 = 80 V. Gehen Sie davon aus, dass alle Bauteile ideal sind, also kein ohmscher
Widerstand R auftritt, und die Messgeräte für Strom und Spannung keinen Einfluss auf den
Schaltkreis haben.
a) Zunächst ist der Schalter in Stellung 1 und der Kondensator C wird geladen. Was ist die
Ladung Q0 im Kondensator, wenn der Ladevorgang beendet ist?
b) Zum Zeitpunkt t = 0 wird der Schalter nun von Stellung 1 in Stellung 2 gebracht. Stellen
Sie mit Hilfe der Kircho↵schen Regeln die Di↵erentialgleichung in Q(t) auf, welche den
Schwingkreis beschreibt. Geben Sie eine geeignete Lösung der Di↵erentialgleichung an. Was
sind die Schwingungsdauer und die Frequenz der auftretenden Schwingung?
11
Name:
SS 2016
c) Wie lautet die entsprechende Funktion für die Stromstärke als Funktion der Zeit I (t)?
d) Wie groß ist die maximale Stromstärke durch die Spule?
12
Name:
SS 2016
Lösung
a) Q0 = U0 · C = 80 V · 50 · 10
6
F = 0.004 C = 4 mC
b) Nutze die Maschenregel:
UC + UL = 0
Q(t)
+ Lİ (t) = 0
C
Q(t)
+ LQ̈(t) = 0
C
1
Q (t) + Q̈ (t) = !02 Q (t) + Q̈ (t) = 0
LC
p
Lösung der Di↵erentialgleichung ist z.B. Q(t) = Q0 cos(!0 t) mit !0 = 1/ LC
p
T = 2⇡!0 1 = 2⇡ LC ⇡ 1.07 s
f =T
c) Es gilt allgemein I (t) =
Mit der Lösung
1
= 0.93 Hz
dQ(t)
d .
Q (t) = Q0 cos (!0 t) = CU0 cos
✓
1
p
t
LC
◆
folgt durch ableiten
I (t) =
Q0 · !0 sin !0 t =
CU
p 0 sin !0 t =
LC
d) Aus der letzten Teilaufgabe folgt direkt I0 =
Alternativ aus der Energieerhaltung:
q
r
C
U0 sin !0 t =
L
C
L U0
1
1
W = CU02 = LI02
2
2
r
C
I0 =
U0 ⇡ 23.5 mA
L
13
I0 sin (!0 t)
Name:
SS 2016
Aufgabe 5
Umkehrprisma (15 Punkte). Oftmals will man die Orientierung eines Bildes durch geeignete optische Instrumente “umdrehen” (z.B. um ein durch ein Mikroskop erzeugtes auf dem Kopf
stehendes Bild richtig herum zu betrachten). Hier betrachten wir den Fall der Bildumkehrung
durch ein sogenanntes Halbwürfelprisma (siehe Skizze).
a) Für die Umkehr des Bildes nutzt man den E↵ekt der Totalreflexion aus. Ab welchem kritischen
Winkel ✓ tritt beim Übergang von Glas mit Brechungsindex nG = 1.46 zu Luft (nL = 1.00)
Totalreflexion auf?
b) Das Licht tre↵e von links senkrecht auf die Prismaoberfläche. Wie wird das Licht gebrochen?
Zeichnen Sie den Strahlengang in der Skizze oben in das Halbwürfelprisma ein.
c) Das Glas weise normale Dispersion auf. Im Bereich des sichtbaren Lichtes nehme der Brechungsindex des Glases von nG,400 = 1.470 für Licht der Wellenlänge 400 nm zu nG,800 =
1.453 für Licht der Wellenlänge 800 nm ab. Wie wirkt sich die Dispersion im konkrekten Fall
auf den Strahlengang im Umkehrprimsa aus?
d) Wie würde sich der Strahlengang durch das Prisma ändern, wenn sich das gesamte Prisma
und das umzukehrende Bild (der Pfeil) in Wasser (mit Brechungsindex n = 1.3) befänden?
14
Name:
SS 2016
Lösung.
a)
nl sin(90 ) = nG sin(✓k )
1 = nG sin(✓k )
✓k = arcsin(
1
)
nG
✓k = 43.2 (= 0.75 rad)
b) Beide Strahlen werden an den Grenzflächen totalreflektiert, da der Einfallswinkel dann jeweils
45 > 43.2 beträgt. Der Pfeil steht anschließen auf dem Kopf.
Gerader Ein-/Ausfall.
2 x 45 -Totalreflexion.
c)
✓k ,400 = 42.86
✓k ,800 = 43.49
Beide Winkel sind kleiner als 45 .
Die Dispersion kann man also vernachlässigen, da die Strahlen senkrecht auf die Prismenoberfläche tre↵en und dann nur noch Totalreflexion auftritt, da der Einfallswinkel von 45 für
alle Wellenlägnen größer als der Grenzwinkel der Totalreflexion ist.
d)
✓k = arcsin(
1.3
) = 62.9
1.46
Der Grenzwinkel betrüge dann ungefähr 63 , sodass keine Totalreflexion mehr an der rechten
Seite des Prismas stattfände.
)
Der Strahl würde dann unter einem Winkel von ✓k = arcsin( 1.46 sin(45
) = 52.57 rechts aus
1.3
dem Prisma wieder austreten
(Alternativ bekommt man auch für eine Skizze des Strahlengangs oder einen richtige Aussage
im Bezug auf nun nicht mehr zu vernachlässigende Dispersionse↵ekte einen Punkt.)
15