Lösung für Blatt 10

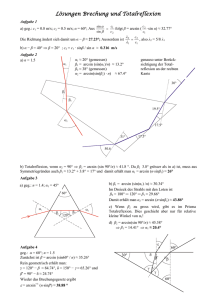
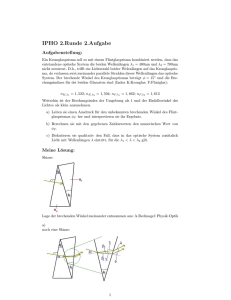
Übungen zu Physik 1 für Ingenieure – Musterlösung Blatt 10
Aufgabe 1 – Brechung
Für Brechung an Medien mit unterschiedlichem Brechungindex n1 und n2 gilt das Gesetz von Snellius
sin(α1 )n1 = sin(α2 )n2
(1)
wobei α1 und α2 die jeweiligen Brechungswinkel bezeichnen. In unserem Fall ist α2 = (90 − 20)◦ , n2 = 1
2 )n2
und daraus fogt
(Brechzahl von Luft) und n1 = 1.33. Aus Gleichung 1 erhält man sin(α1 ) = sin(α
n1
α1 = 44.95◦ .
Die scheinbare Höhe des Gegenstandes bestimmt man gemäß Abbildung 1 folgendermaßen. Die Seitenlänge
b
zu b = 3.993m. Damit folgt für die Seitenlänge c aus tan(β) = cb , dass
b ergibt sich aus tan(α1 ) = 4m
c = 1.453m.
Aufgabe 2 – Prisma
(a) Am oberen Dreieck in Diagramm 2 sieht man: 2 + α = 180◦ und 2 + 2β = 180◦ . Addiert man beide
Gleichungen, so ergibt sich β = α2 In diesem Fall wird das Prisma symetrisch durchlaufen
(b) Das Gesetz von Snellius liefert sin(θ) · nL = sin(β) · n0 mit nL = 1 (Brechzahl von Luft). Daraus ergibt
sich folgender Einfallswinkel: θ = arcsin (sin β · 1.5) = 48.59◦
(c) Es gilt γ + β = θ (siehe Zeichnung auf dem Übungsblatt), β = α2 und δ = 2γ. Daraus folgt δ+α
2 = θ
und schließlich δ = 2θ − α = 37.18◦
α
(d) Es gilt (siehe Aufgabenblatt) sin α+δ
2 = n(λ) sin 2 . Aufgelöst nach δ ergibt sich
α
δ = 2 arcsin n(λ) sin
−α
(2)
2
Für rotes Licht gilt: n(λ) = 1.48. Eingesetzt in Gleichung 2 erhält man δrot = 35.46◦
Für violettes Licht gilt: n(λ) = 1.52 Eingesetzt in Gleichung 2 erhält man δviolett = 38.93◦
Schließlich ergibt sich für die Winketrennung: δviolett − δrot = 3.47◦
Aufgabe 3 – Totalreflexion
(a) Bei Totalreflexion tritt keine Brechung sondern ausschließlich Reflektion auf. Beim Übergang zwischen
Medien mit der Brechzahl n1 und n2 muss für α2 in Gleichung 1 gelten: α2 = 90◦ . Damit vereinfacht sich
Gleichung 1 zu
n2
α1 = arcsin
.
(3)
n1
In diesem Fall ist n2 = 1 (Brechzahl von Luft) und n1 = 1.5 (Brechzahl von Glas). Schließlich ergibt sich
α1 = 41.81◦ . Das ist der kritische Winkel für Totalreflexion beim Übergang zwischen Glas und Luft.
(b) Das Licht wird unter dem Winkel 180◦ − 2α1 = 96.4◦ gegenüber dem eingestrahlten Licht abgelenkt.
(c) Wieder benutzt man Gleichung 3 mit den Brechungindezes nW = 1.33 für Wasser und nG = 1.5 für
Glas. Die kritischen Winkel sind:
L
beim Übergang von Wasser in Luft: α = arcsin nnW
= 48.75◦
nW
beim Übergang von Glas in Wasser: α = arcsin nG = 62.46◦
1
Abbildung 1: Zeichnung zu Aufgabe 1
Abbildung 2: zu Aufgabe 2
2