WIEDERHOLUNG WESENTLICHER BEREICHE:

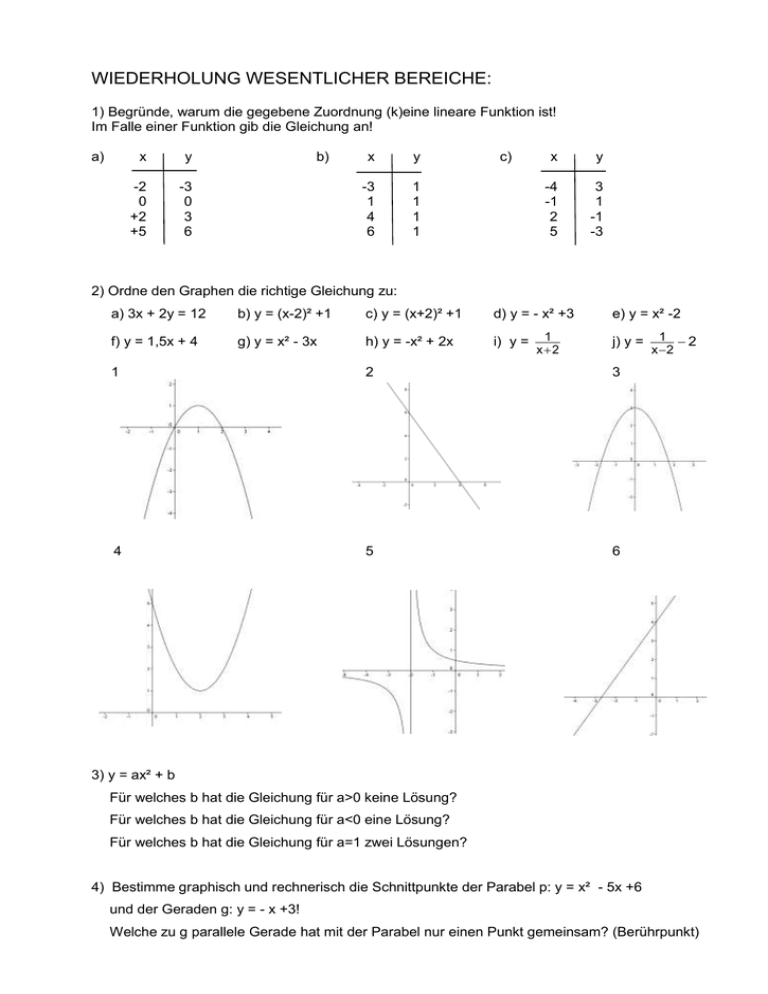
WIEDERHOLUNG WESENTLICHER BEREICHE:
1) Begründe, warum die gegebene Zuordnung (k)eine lineare Funktion ist!
Im Falle einer Funktion gib die Gleichung an!
a)
x
y
-2
0
+2
+5
-3
0
3
6
b)
x
y
-3
1
4
6
1
1
1
1
c)
x
y
-4
-1
2
5
3
1
-1
-3
2) Ordne den Graphen die richtige Gleichung zu:
a) 3x + 2y = 12
b) y = (x-2)² +1
c) y = (x+2)² +1
d) y = - x² +3
f) y = 1,5x + 4
g) y = x² - 3x
h) y = -x² + 2x
i) y =
1
x2
e) y = x² -2
j) y =
1
2
3
4
5
6
1 2
x 2
3) y = ax² + b
Für welches b hat die Gleichung für a>0 keine Lösung?
Für welches b hat die Gleichung für a<0 eine Lösung?
Für welches b hat die Gleichung für a=1 zwei Lösungen?
4) Bestimme graphisch und rechnerisch die Schnittpunkte der Parabel p: y = x² - 5x +6
und der Geraden g: y = - x +3!
Welche zu g parallele Gerade hat mit der Parabel nur einen Punkt gemeinsam? (Berührpunkt)
5)
Wie können Nullstellen und Scheitel einer quadratischen Funktion bestimmt werden?
Zeige die verschiedenen Lösungsmöglichkeiten an einer Graphik!
6)
Bestimme die Gleichungen der
beiden Graphen und schreibe
einen passenden Text
zu dieser Aufgabe!
7) Die Einfahrt nach Graz über die Ries hat ein Gefälle von 14%.
Welchen Höhenunterschied überwindet man dabei auf einer Länge von 800 m?
a) –1 sin 1
b) sin² + cos²= 1
8)
Begründe:
9)
Wie hängen der pythagoreische Lehrsatz und der Cosinussatz zusammen?
10) Begründe, warum die Gleichungen keine Lösung haben!
a) sin²+ cos² = 2
b) sin²- cos² = 1,5
11) Für welches c  R hat die Gleichung sin = c zwei Lösungen?
In welchen Quadranten liegen die Lösungen, wenn c < 0 bzw. c>0 ist?
12) Leite die trigonometrische Flächenformel für das Dreieck her!
Formuliere sie allgemein!
13) In einen Berg werden vom gleichen Punkt aus zwei geradlinige Stollen getrieben, die
miteinander einen Winkel von 30° einschließen.
Der eine Stollen ist 5km, der andere ist 7 km lang.
Wie weit sind die Endpunkte der beiden Stollen voneinander entfernt?
3,66 km
14) Eine gerade quadratische Pyramide hat die
Grundkantenlänge 6,8 und die Höhe h=9,5.
Berechne
a) den Neigungswinkel einer Seitenkante zur
Grundfläche (= Winkel zur Diagonale)
b) den Neigungswinkel einer Seitenfläche zur Grundfläche und
c) den Winkel, den Seitenkante und Grundkante miteinander einschließen.
15) Auf einem Turm (h = 20 m) ist ein Blitzableiter montiert.
Von einem 30 m vom Fußpunkt F des Turms entfernten Punkt sieht man diesen
Blitzableiter unter einem Sehwinkel von 3,8°.
Zeichne eine Skizze und bestimme die Höhe des Blitzableiters!
63,15°
71,37°
70,31°
3m
16) Ein Wanderer geht mit einer durchschnittlichen Geschwindigkeit von 3,2 km/h in Richtung
N31°0. Nach 3,5 h ändert er seine Richtung auf N17°O und geht um 0,1 km/h langsamer.
2 Stunden nach dieser Richtungsänderung erreicht er sein Ziel.
Wie lang ist die direkte Verbindungslinie (Luftlinie) zwischen Start und Ziel?
17,3 km