Raten-Theorie chemischer Reaktionen
Werbung
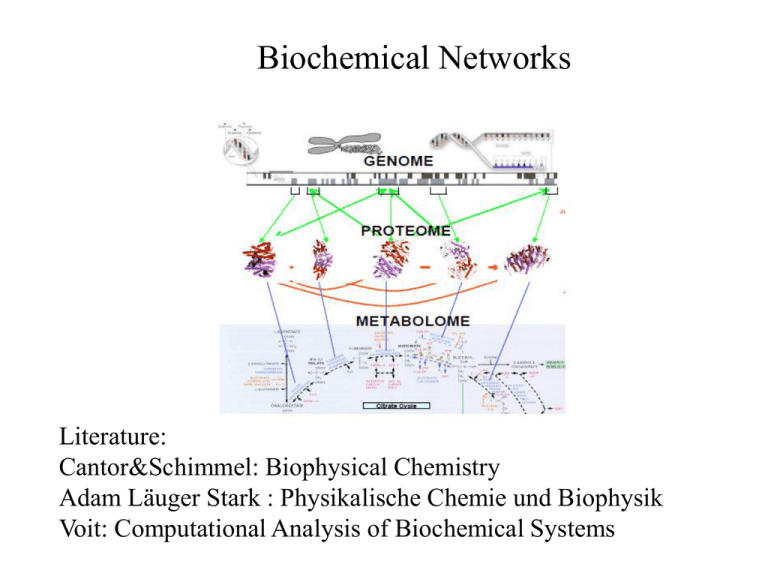
Biochemical Networks Literature: Cantor&Schimmel: Biophysical Chemistry Adam Läuger Stark : Physikalische Chemie und Biophysik Voit: Computational Analysis of Biochemical Systems Modelling Biochemical Networks A B k kAB Cooperative Enzymes Inhibition, Regulation Kinetic Rates Synergistic Systems Parameter Estimations BA k1 k2 E S ES E P k1 Literature: Voit: Computational Analysis of Biochemical Systems Adam Läuger Stark : Physikalische Chemie und Biophysik Breckow : Biophysik Open Systems Cellular Images of DNA Hybridization Kinetics In Vivo Ingmar Schön & Dieter Braun PNAS, accepted (2009) experimental setup lock-in detection scheme periodic illumination phase-locked relative to perturbation quantum efficiency illumination 0° collect fluorescence by slow CCD (low-pass filtering) 90 ° 180 ° 270 ° fit with transfer function for a first-order reaction approach goal: measure reaction kinetics in vivo principle: perturbe equilibrium and analyze relaxation detection: fluorescence resonance energy transfer (FRET) DNA probe RhG | 5’-C AGG TTA CTA TCG TAT T C-3’ ROX | 5’-C AAT ACG ATA GTA ACC T C-3’ C = L-enantiomeric cytosin DNA probe hybridization kinetics in a single living cell different kinetics in subcellular compartments dependence on concentration calibration brightness of confocal image vs. DNA concentration dependence on concentration calibration brightness of confocal image vs. DNA concentration 1 koff kon cA cB comparison in vitro vs. in vivo 1 koff kon cA cB … faster Hybridization in vivo! However 12bp probe… … is slower: Binding with Proteins ! Molecular Crowding is no significant for short DNA Trivial molecular crowding: excluded volume enhances local concentration, however both for 12 & 16 mer => Not found Length dependent, specific interactions: - Catalytic speed up of Hybridization - Slowing by specific binding => Less free concentration and slower kinetics Das Prinzip des detaillierten Gleichgewichts In einem komplexeren Netzwerk (z.B. ein zyklisches System) sind Reaktionen mit dx/dt=0 denkbar, die thermodynamisch zugelassen wären, aber einen permanenten Materialfluss ermöglichen würden. Die Gleichgewichtsbedingung gilt für alle Teilreaktionen eines Systems. „Das Gleichgewicht ist wegunabhängig“ Prinzip des detaillierten Gleichgewichts (Prinzip der mikroskopischen Reversibilität) Michaelis-Menten Kinetics Biologische Regulation durch Enzymhemmung Effects of noncompetitive inhibition Non-competitive inhibition Competitive Inhibition Inhibitor competes with substrate for binding to enzyme Example 1: most drugs Example 2: Product inhibition Problem : Die kompetitive Hemmung hat unzureichende Regeleigenschaften Mehrfachbindung und die Regulation biologischer Aktivität „Abschaltfunktion“ Rate als Funktion der inhibitorischen Substanz Ein Enzym mit mehreren Bindungsstellen für ein hemmende Substanz B ermöglicht schärfere Regelung Sollwert Kooperativität allosterischer Enzyme Michaelis-Menten-Kinetik (n=1) Vmax sn vP n K M sn Hill Gleichung Der Hill-Koeffizient wird aus experimentellen Daten v(s) bestimmt durch logarithmische Auftragung: (Hill Plot) V n ln s n ln K M ln Vmax V Das Operon-Regelsystem nach Monod: Beispiel allosterischer Kontrolle G: Genprodukt (z.B. Enzym, das Bildung von P aus Substrat St katalysiert) Für die Komplexbildung von Produkt P mit Konzentration yP und dem regulatorische Gen R wird eine kooperative Rückkopplung angesetzt Autokatalyse, Voltera-Lotka Systeme Die DGL ohne Rückkopplung lautet : dy A k10 k11y A k2 dyB k21 y A k 22 y B k2 Der autokatalytische Schritt erzeugt die Nicht-Linearität k10 y A k11 k21 y B und dy A yA yA yB dt dy B yA yB yB dt Räuber-Beute-System Nicht-Lineare Systeme können mehrere stationäre Zustände aufweisen: Diskriminative Schaltfunktion Relationships (Shiraishi-Savageau, 1992) Kinetic orders = weighted averages of more elementary ko´s (Alves-Savageau, 2000) Homogeneous 3D reactions -> pos. integers Modellierung Biochemischer Netzwerke Quelle: Stelling, Curr.Op.MicroBio 2004 Metabolische Netzwerke Metabolische Netzwerke sind durch eine Netzwerktopologie (pathway) und biochemische Ratengleichungen beschrieben. Computergestützte Analyse S-Systeme : einfache nichtlineare Näherung mit numerischen Vorteilen Elementare Fluss Moden Analyse : Stoichiometrisches Fliessgleichgewicht S-Systeme • Produktansatz für die Zu- und Abflüsse Vi+ and Vi-. dXi/dt = V+-V-=ai j=1n+m Xjgij - bi j=1n+m Xjhij ai und bi : Raten Konstanten - gij and hij : Kinetische Exponenten – Xi : Konzentrationen of all the metabolites that are involved in Warum funktionieren S-Systeme ? Begründete Annahmen: Biochemische Systeme sind in der Regel in einem Quasistationären Zustand, d.h. die Dynamik der Systemsteuerung ist langsam gegenüber der zugrundeliegenden Systemdynamik. S-Systeme sind Entwicklungen um stationärem Gleichgewicht Biochemische Systeme sind robust. D.h. die Funktionen sind weitestgehend unabhängig von den Konzentrationen Vorteile: * Analytische Steady-State-Lösung * Mathematisch und rechnerisch einfach * Beliebige Differentialgleichungssystem können in äquivalente S-Systeme übersetzt werden. * Parameterschätzung möglich aus Torres: Pathway Analysis Parameterschätzung Bestimmung der kinetischen Ordnung aus experimentellen Daten dlnv v X g dln X X v Die Stoichiometrische Matrix: Flussanalyse dS Nv dt