Skript § 1

1
§ 1 Entwicklung der Schrift- und Zahlzeichen
Bevor wir uns mit den ersten ”mathematischen” Fragestellungen beschäftigen können,
stellen wir erst einmal zusammen, welch langer, mühsamer Weg notwendig war, um zu
den heute benutzten Zeichen des Dezimalsystems zu kommen.
a) Zahlzeichen der Sumerer und Babylonier
Man geht davon aus, dass die Menschen im alten Nahen Osten ca. 8000 v. Chr. die ersten Versuche unternahmen, über die urtümliche Daseinsform des Jägers und Sammlers
hinauszugelangen. Die Nahrungsproduktion und die Domestikation von Tieren erlaubten es, sich mehr oder minder dauerhaft in einem bestimmten Gebiet niederzulassen. Der
Übergang vom nomadischen zum sesshaften Leben vollzog sich nicht abrupt; in Dscharmo
(entnommen aus [TiL5]), einer Siedlung im heutigen Nordostirak, fanden Archäologen
in einer Grabungsschicht, die auf das Jahr 7000 v.Chr. datiert wurde, sowohl Reste von
2
wildwachsenden Nahrungspflanzen als auch von Kulturpflanzen sowie auch Reste von
Haustieren. In jüngeren Grabungsschichten finden sich dann auch überreste von Steinund Knochengeräten, flachen Mahlsteinen und einfachen Tongefässen.
Die Geschichte der Schrift- und Zahlzeichen beginnt zwischen Euphrat und Tigris in
Mesopotamien. Das Gebiet zwischen Bagdad und dem Persischen Golf besteht vom 6. bis
zum 2. Jahrtausend v. Chr. aus zwei Reichen: dem Land Sumer im Süden und dem Land
Akkad im Norden (vgl. die obige Karte). Obwohl die Sumerer und die Akkader benachbart
sind, sprechen sie zwei Sprachen, die so verschieden sind wie Deutsch und Chinesisch.
Um 3500 v.Chr. bauten die Bürger von Uruk, einer Stadt in Südmesopotamien, eine Siedlung aus luftgetrockneten Lehmziegeln für Tausende von Einwohnern. Die Menschen von
Uruk erdachten ein System zur Aufzeichnung ihrer geschäftlichen Transaktionen in Form
von Piktogrammen, die in Tontäfelchen eingeritzt wurden. Die Sumerer und speziell die
Einwohner von Uruk hatten zu schreiben begonnen. Die Piktogramme der ersten Täfelchen, die auf 3300 v.Chr. datiert werden und von denen zwischen 500 und 600 gefunden
wurden, stellen verschiedene Waren dar, z.B. Fische, Milchkannen, Schweine, Kühe, Schafe oder Ziegen. Ausserdem gibt es Vertiefungen unterschiedlicher Form und Größe; sie
bezeichnen die jeweiligen Mengen der Waren; man könnte also die Tontäfelchen als Warenbegleitbrief betrachten.
(entnommen aus [TiL5]). Man geht davon aus, dass die ”Schriftzeichen” mit einem spitzen
Gegenstand ziemlich tief in den feuchten Ton der Täfelchen eingeritzt wurden. Die anderen
Zeichen, die sich als Zahlzeichen herausstellten, wurden mit einem Schreibrohr – einem
Schilfrohr oder einem Stäbchen aus Knochen oder Elfenbein – hergestellt, das an einem
Ende abgerundet und am anderen Ende spitz zugeschnitten war. Diese Griffel, von denen
einer einen Durchmesser von ca. 4 mm und ein anderer einen Durchmesser von ca. 1
3
cm hatte, wurden unter einem bestimmten Winkel (senkrecht oder schräg) in den Ton
gedrückt. Dadurch entstanden kleine und große runde Abdrücke bzw. kleine oder große
”Kerben”.
(Entnommen aus [Ifr1]) Ich werde diese Zeichen folgendermaßen schreiben:
∪ für eine kleine Kerbe,
S
für eine große Kerbe,
◦ für einen kleinen runden Abdruck,
für einen großen runden Abdruck.
Außerdem gab es noch zwei weitere Zeichen: eine große Kerbe mit einer Vertiefung in der
Mitte, d.h. einem kleinen runden Abdruck in der Mitte und ein großer runder Abdruck
mit einer kleiner runden Vertiefung in der Mitte.
S
◦
und
◦
Neben diesen Zeichen gab es auch Zeichen für bestimmte Tiere, z.B.
für Schaf und
für Ziege oder
für Kuh
(entnommen aus [Ger1] bzw. [Ger3]). Es gibt aber auch Zeichen, für die es keine Erklärung gibt. Zeichen und Ziffern waren in der Regel in zwei oder mehreren waagerechten
Reihen angeordnet. Die Ziffern standen in den Kästchen meistens oben, von rechts ausgehend. Wie ist man auf die Bedeutung der einzelnen Zeichen, speziell der Zahlzeichen
gekommen? Die Forscher haben auf Grund der Tatsache, dass die sumerischen Schreiber
häufig auf der Rückseite der Tontafeln das Ergebnis der Zählungen auf der Vorderseite
zusammenfassend aufgeführt haben, die Bedeutung der entsprechenden Zeichen herausgefunden. Das Zeichen ∪ kam bis zu 9 mal vor, woraus man geschlossen hat, dass es die
Zahl 1 repräsentieren sollte. Wir nehmen an, dass wir schon wissen, dass das Zeichen ◦
10 bedeutet, und demonstrieren an einem Bespiel, wie man die Bedeutung von weiteren
Zeichen finden kann.
Eine in Uruk entdeckte Tontafel (um 2850 v. Chr.) trägt auf der Vorderseite einzelne
Angaben über abgezählte Säcke verschiedener Waren und Geflügel, auf ihrer Rückseite
die Summe der Anzahl des Geflügels und der Säcke.
4
(Entnommen aus [Ifr1]) Mit Hilfe dieser Tafel wollen wir den Wert für die große Kerbe
bestimmen. Da sowohl auf der Vorderseite als auch auf der Rückseite die Angaben für
das Geflügel identisch sind (ein kleiner runder Abdruck und 5 kleine Kerben sowie das
Piktogramm für Geflügel), betrachten wir nur die Angaben zu den Säcken.
Wir erhalten auf der Vorderseite
15 (ein kleiner runder Eindruck und 5 kleine Kerben) + 30 (3 kleine runde Eindrücke)
[
[
+
+ 40 (4 kleine runde Eindrücke) =
+85 .
Auf der Rückseite sind
[
[
2
+ 20 (2 kleine runde Eindrücke) + 5 (5 kleine Kerben) = 2 +25
Säcke angegeben.- Durch Gleichsetzen erhalten wir die Beziehung
[
[
+85 = 2 +25
und hieraus den gesuchten Wert für die große Kerbe:
[
= 60 .
Als gesichert S
kann man dieses Ergebnis aber erst dann betrachten, wenn sich auf anderen
Tontafeln zu = 60 kein Widerspruch ergibt. Dies ist der Fall. So ergaben sich folgende
Werte für die sumerischen Ziffern:
[
[
∪ = 1, ◦ = 10,
= 60, ◦ = 600, = 3600 und ◦ = 36000 .
Zwischen 2700 und 2600 v. Chr. wurden die Zeichen um 90◦ gegen den Uhrzeigersinn
gedreht.
5
(Entnommen aus [Ifr1]) Die ersten neun natürlichen Zahlen wurden durch entsprechende
Wiederholung des Zeichens ∪ (um 90◦ gegen den Uhrzeigesinn gedreht) für die 1 dargestellt, die Zahlen 20, 30, 40 und 50 durch entsprechende Wiederholung des Zeichens
S◦ für
die 10, die Zahlen 120, 180, 240, 300 durch die entsprechende Anzahl des Zeichens (um
90◦ gegen den Uhrzeigesinn gedreht) für die Zahl 60 usw.
Durch die Einführung eines neuen Schreibrohrs, dessen Ende die Form eines flachen Lineals
hatte, entstanden die Keilschrift-Ziffern, die spitz zulaufende Formen hatten.
(entnommen aus [Jean]). Es ist weiter denkbar, dass der Schreiber im Laufe der Zeit
die Bild- und die Zahlzeichen alle mit dem einen angeschärften Griffel erzeugte. Kerben
und runde Abdrücke wurden durch ”Nägel” bzw. ”Keile” und ”Winkel” ersetzt. Man
konnte durch unterschiedlich tiefe Eindrücke im Ton große und kleine Nägel bzw. Winkel
erzeugen.
- 1 wurde durch einen kleinen senkrechten Nagel O
| statt durch eine kleine Kerbe
dargestellt;
- 10 wurde durch einen Winkel ≺ statt durch einen kleinen runden Abdruck dargestellt;
- 60 wurde durch einen größeren senkrechten Nagel 5
| statt durch eine große Kerbe
dargestellt;
- 600 wurde durch einen größeren senkrechten Nagel und einen Winkel 5
| ≺ dargestellt;
- 3600 wurde durch ein Vieleck aus vier Nägeln statt eines großen runden Abdrucks
dargestellt.
6
Ob allerdings ein Keil klein oder groß ist, kann man nur dann entscheiden, wenn bei der
Darstellung einer Zahl beide Typen verwendet werden.
5
| O| O|
bedeutet z.B. 62. Sind die Nägel dagegen gleich groß, so kann
5
| 5
| 5
|
sowohl die Zahl 3 als auch die Zahl 62 bedeuten. Die Sumerer verwendeten später gleich
große Zeichen und versuchten dann die Verwechslungsmöglichkeiten durch Abstände zwischen den Zeichen zu verhindern. So schrieben sie z.B.
5
| 5
| 5
|
für die Zahl 3, aber
5
|
5
| 5
|
für die Zahl 62. Dieses Problem taucht eigentlich aber schon bei der Darstellung der
Zahlen mit Kerben und runden Eindrücken auf. Auch bei Darstellung der Zahl 60 kann
es Probleme geben. Stehen der Keil und der Winkelhaken nicht ganz nahe beieinander,
so kann z.B.
5
| ≺
auch 60 + 10 = 70 bedeuten. Wenn also alle Keile gleich groß sind, so kann
5
|
verschiedene Bedeutungen haben. Entsprechendes gilt für den Winkelhaken. 5
| bedeutet
also die Zahl 1, 60 oder eine Potenz von 60 oder auch einen Bruchteil von 1, nämlich 1/60
oder (1/60)2 usw..
Der Winkelhaken ≺ bedeutet die Zahl 10 oder 600 oder auch 10/60 usw..
Das Zahlssystem der Sumerer, ein sog. Sexagesimalsystem, ist also eigentlich ein gemischtes Zehner- und Sechsersystem. Dass als erste Stufe die Zusammenfassung von 10 Zeichen
für die Zahl 1 zu einem neuen Zeichen eingeführt wurde, ist nicht weiter verwunderlich,
da wahrscheinich alle Völker als Hilfsmittel die Finger zum Zählen mitbenutzt haben.
Warum die Sumerer als zweite Stufe der Bündelung die 6 gewählt haben, darüber kann
man nur spekulieren. Eine plausible Begründung wäre die folgende, die darauf aufbaut,
dass die Zahlen gleichzeitig eine gute Beschreibung des Gewichtssystems liefern sollten.
Man kann sich vorstellen, dass in jener Zeit drei verschiedene Gewichtseinheiten benötigt
wurden:
1. Ein kleines Gewicht für Gewürze oder auch Edelmetalle, etwa 7 bis 8 g schwer.
2. Ein Haushaltsgewicht von etwa 1/2 kg.
3. Ein Gewicht, das der Last entspricht, die ein Mann tragen kann:
ungefähr 30 kg = 60 Pfund.
7
Wenn man die Beziehung der einzelnen Gewichtseinheiten zueinander so festlegen will,
dass das ungefähre Verhältnis erhalten bleibt und möglichst viele Anteile des größeren
Gewichts ganzzahlige Vielfache des kleineren Gewichts sind, so wird man auf die Zahl 60
geführt. 60 ist durch 2, 3, 4, 5, 6, 10, 12, 15, 20 und 30 teilbar.
Wir schauen uns noch ein paar Beispiele für Zahlen im Sexagesimalsystem an: wir betrachten
555
5 ≺≺ | | |
|
5
|
Dies kann bedeuten:
1 · 601 + 24 · 60o = 84
oder
1·
1
1
84
+ 24 · 2 =
60
60
360
oder
1 · 600 +
24
24
=1 .
60
60
Aus dem Zusammenhang ging immer klar hervor, welche Zahl gemeint war, wenn alle
”Stellen” vertreten waren. Unklarheiten entstanden aber, wenn eine Stelle oder sogar
mehrere Stellen fehlten. So entwickelten sich im Laufe der Zeit besondere Formen, um
diese Unklarheiten zu beseitigen. Zunächst wurde z.B. die Zahl 4 in der Form
OOO
| | |
O
|
OOO
und nicht in der Form O
| | | | geschrieben, denn letzteres könnte auch
1 · 601 + 3 oder 2 · 601 + 2 oder 3 · 601 + 1 oder ...
bedeuten. Durch Auseinanderrücken der Zeichen wurde in vielen Fällen die Darstellung
eindeutig(er). So schrieben die Babylonier 2 · 601 + 2 in der Form O| O| O| O
| oder 7424 in
der Form
OO
OOO ≺≺≺ OOOO
≺
| |
| | |
| | | |
2 · 602
= 7200
3 · 601
= 180
4 · 101
= 40
4 · 100
=4
Um die Zahl 7204 = 2 · 602 + 4 zu schreiben benötigt man nur 6 Keile, die durch einen
großen Zwischenraum getrennt werden müssen. Aber wie kann man dem Zwischenraum
ansehen, dass sowohl die ”60-er” als auch die ”10-er” fehlen.
8
In den Susa-Texten ( 23 Tafeln mathematischen Inhalts, die aus der Zeit kurz nach Hammurabi stammen, der 1792 v.Chr. an die Macht gelangte und ca. 30 Jahre lang Tempel,
Verteidigungswälle und Bewässerungskanäle baute) wird an Stelle des Freiraums auch ein
≺
spezielles Leerzeichen, nämlich ≺ (zwei kleine Winkelhaken) benutzt. So lässt sich z.B.
7242 in der Form
≺≺≺ OO
OO ≺
| | ≺
| |
≺
schreiben.
Bemerkenswert ist auch, dass schon sehr früh ein Zeichen für Minus benutzt wird, nämlich
ein kleiner querliegender Keil
B− ;
so findet man z.B. für die Zahl 19
<<
B− O
| .
Es gibt auch schon in ältester Zeit Anzeichen für ein neues Dezimalsystem mit besonderen
Zeichen für 100 und 1000. In ”wissenschaftlichen” Texten wird aber ausschliesslich das
sexagesimale System geschrieben.
Aus den Piktogrammen entwickeln sich im Laufe der Zeit Gebilde, die aus Keilen zusammengesetzt sind; daher kommt der Name Keilschrift. Die Form der Gebilde ist allerdings
nicht dem Schreiber überlassen; es gibt ganze Register, in denen die Form der Gebilde
festgelegt ist. Jedes Gebilde kann (zunächst) je nach Zusammenhang verschiedene Bedeutungen haben. Nach und nach verbindet sich nur noch eine Bedeutung mit einem Gebilde.
Bald sind es nur noch 600 Zeichen.
(Entnommen aus [Ifr1]) An dieser Stelle möchte ich darauf hinweisen, dass sich die Verwendung der Zahlzeichen bei den Sumerern und den Babyloniern nicht alleine auf die Angabe
von Anzahlen bestimmter Gegenstände beschränkte; schon sehr früh hat man ”geometrische” Aufgaben gelöst, bei denen es z.B. um die Inhalte von Teilen eines Quadrats
9
oder Dreiecks geht (vielleicht im Zusammenhang mit Felderteilung). Es gibt Aufgaben zu
Systemen linearer Gleichungen oder etwa zum ”Satz des Pythagoras” in folgender Form
(entnommen aus [Ger1] bzw. [Ger3]):
”Ein Balken 30,
Von oben ist er 6 herabgekommen
Von unten was hat er sich entfernt?
30 quadriere, 15 siehst du.
6 von 30 abgezogen, 24 siehst du.
24 quadriere, 9,36 siehst du.
9,36 von 15 ziehe ab. 5,24 siehst du.
5,24 hat was als Quadratwurzel? 18.
18 am Boden hat er sich entfernt.”
Zur Erläuterung machen wir uns folgende Beziehungen klar:
302 = 900 = 15 · 601
242 = 576 = 9 · 601 + 36
900 − 576 = 5 · 601 + 24 = 324 = 182 .
In den nachfolgenden Zeilen wird folgendes berechnet:
”Wenn er sich 18 am Boden entfernt hat,
wieviel ist er herabgekommen?”
Wie man auf die Rechenvorschrift gekommen ist, ist unbekannt. Im zweiten Teil des Textes
wird eine Probe durchgeführt.
Aufgaben aus dem Bereich der Algebra hatten bei den Babyloniern folgende Form:
1
1
addiert, er
- ”Ich fand einen Stein, ich habe ihn nicht gewogen. Ich habe und
7
11
wog 1 Mine.”
Das führt auf die Gleichung
x
1 x
x+
+
x+
=1.
7
11
7
Die Aufgabe wird folgendermaßen gelöst:
Durch Multiplikation mit 7 entsteht die Gleichung
(7x + x) +
d.h.
8x +
1
(7x + x) = 7 ,
11
1
· 8x = 7 ,
11
10
und daraus durch Multiplikation mit 11
88x + 8x = 77 ,
also
96x = 77 .
- ”Ich habe von der Fläche die Seite meines Quadrates subtrahiert und es ist 14 12 .”
Das führt auf die Gleichung
1
x2 − x = 14 .
2
2
2
- ”Ich habe die Fläche von 2 Quadraten addiert, es ist 16 . Die Seite des einen ist
3
3
der Seite des anderen. Ich habe 10 von der Seite des kleineren Quadrates subtrahiert.
Was sind die Seiten des Quadrates?”
Das führt auf die Gleichung
2
x2 + y 2 = 16 ;
3
2
y = x − 10 .
3
b) Zahlzeichen der Ägypter
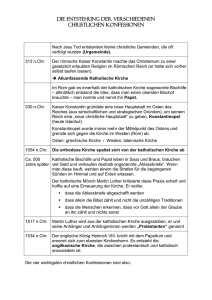
Im Jahre 2900 v.Chr. werden Oberägypten (Niltal von Assuan an) und Unterägypten
(Nildelta) durch den König Narmer geeint. Auf einer Platte wird die Unterwerfung von
Unterägypten dargestellt. Diese Platte enthielt die ältesten bekannten ägyptischen Schriftund Zahlzeichen. Es wurden folgende Zeichen benutzt:
|
für
1
(Strich oder Finger)
für
10
(Fessel)
für
100
(Strick)
für
1000
(Lotuspflanze)
für
10000
(Finger)
für
100000
(Kaulquappe)
für 1000000
Auf einer Keule des Königs Narmer steht z.B., dass Narmer
120 000 Gefangene gemacht sowie
400 000
Rinder und
1 422 000
Ziegen erbeutet hat.
(Gott)
11
(entnommen aus [Ger1] bzw. [Ger3]).
Um z.B. die Zahl 2 800 000 zu schreiben, hätte man 2 Götter und 8 Kaulquappen benötigt.
Im mittleren Reich (12. Dynastie, 1991-1783) wird eine ”multiplikative Schreibung” eingeführt. Man fasst 2800000 auf als 28 · 100000 und schreibt dafür unter eine Kaulquappe
die Zahl 28, d.h.
In dieser Form wurden die Zahlen nur auf Denkmälern aus Stein oder Holz geschrieben.
In der Literatur werden sie als hieroglyphische Zahlzeichen bezeichnet. Wenn Zahlen (mit
Tusche) auf Papyrus geschrieben wurden, so benutzte man vereinfachte Zeichen, die sog.
hieratischen Zeichen (vgl. Folie 1, entnommen aus [Trop]). Man kann sie teilweise als
Vorstufe zu ”Individual-Zahlzeichen” ansehen, die die Anzahl der Striche oder der anderen
Grundfiguren nicht mehr direkt erkennen lassen.
Aus der Zeit, bevor die Hyksos (Der Name bedeutet ”Herrscher fremder Völker”, wahrscheinlich Fremdländische aus Palästina, 15. Dynastie, vgl. Zeittafel, Folie 2, entnommen
aus [TiL5], [TiL3] und [TiL1]) die Herrschaft in Ägypten übernahmen, stammen die erhaltenen Abschriften der beiden wichtigsten mathematischen Papyri:
(1) Der Papyrus Moskau, genannt nach seinem Aufbewahrungsort, dem Museum der
Schönen Künste in Moskau, ist 5,44 m lang und 8 cm breit. Er enthält ungeordnet
25 Aufgaben, meist aus dem täglichen Leben. Er wurde von einem Schreiber der 13.
Dynastie (1783-1640) nach einer Vorlage aus der Zeit der 12. Dynastie (1991-1783)
geschrieben.
(2) Der Papyrus Rhind ist etwas jünger, genannt nach seinem ersten Besitzer; er ist
5,34 m lang und 33 cm breit und wird im Britischen Museum in London aufbewahrt, dazu einige Fragmente in New York. Er enthält eine Liste der Divisonen n2
und 84 Aufgaben in lehrbuchartiger Anordnung. Er beginnt mit den Worten: ”Genaues Rechnen. Einführung in die Kenntnis aller existierenden Gegenstände und
aller dunklen Geheimnisse. - Dieses Buch wurde geschrieben im Jahr 33, im vierten Monat der Überschwemmungsjahreszeit unter seiner Majestät dem König von
12
Ober- und Unterägypten Apophis aus der Hyksoszeit (etwa 1640 - 1540) mit Leben
versehen, in Anlehnung an eine alte Schrift aus der Zeit des Königs von Ober- und
Unterägypten Anenemhet III. Der Schreiber A’h-mosè hat die Abschrift angefertigt”.
Darüber hinaus gibt es noch zahlreiche jüngere Papyri, z.B. die von Kahun, Berlin, Reisner
oder Akhmim sowie eine mathematische Lederrolle, die im Britischen Museum aufbewahrt
wird.
Die Multiplikation und die Division führen die Ägypter immer auf die einfachen Operationen ”Verdoppeln” und ”Halbieren” zurück. Wir wollen dies an einem einfachen Beispiel
demonstrieren (entnommen aus [RoSh]).
a) Wir berechnen das Produkt aus 47
47 auf:
1
2
4
8
16
32
und 33. Dazu schreiben wir die Vielfachen von
×
×
×
×
×
×
|
47
|
94
| 188
| 376
| 752
| 1504.
Wegen 33 = 1 + 32 werden links die Zahlen markiert, die bei der ”Dualdarstellung”
von 33 benötigt werden. Wir erhalten also:
|
1
2
4
8
16
| 32
×
×
×
×
×
×
|
47
|
94
| 188
| 376
| 752
| 1504.
Durch Addition der rechts stehenden Zahlen in den angestrichenen Zeilen ergibt sich
das Ergebnis : 47 · 33 = 47 + 1504 = 1551 .
b) Wir berechnen den Quotienten aus 47 und 33. Dazu schreiben wir die Teile von 33
auf:
1 − mal
| 33
1
− mal
| 11
3
1
− mal
| 3.
11
Wegen 33 + 11 + 3 = 47, d.h. 33 · (1 + 1/3 + 1/11) = 47 erhalten wir
47/33 = 1 + 1/3 + 1/11.
Die Ägypter arbeiten bei Brüchen fast ausschliesslich mit Stammbrüchen; sie benutzen
dafür die Zahlen des ”Dezimalsystems” und setzen über die Zahl das Zeichen ◦, also z.
◦
B. n.
13
2
Da die Ägypter immer mit Stammbrüchen rechnen möchten, ist kein Ergebnis, sondern
5
eine Divisionsaufgabe, die als Summe von Stammbrüchen geschrieben werden muss. Das
2
ist auch der Grund, warum sich im Papyrus Rhind eine Tabelle der Divisionen für alle
n
ungeraden Zahlen 5 ≤ n ≤ 101 befindet.
Für einige Brüche gibt es Sonderzeichen, nämlich (vgl. [Ger1] bzw. [Ger3]):
2
1
1
Bei der Zerlegung wird die ”kanonische” Zerlegung
= + vermieden. Es ist aber
n
n n
nicht klar, welchen Gesetzmäßigkeiten die Zerlegungen folgen. Man könnte bei einigen
Zerlegungen von folgender Vorstellung geleitet werden: wenn man zum Beispiel 2 Brote
auf 7 Personen verteilen möchte, so teile man jedes Brot in 4 gleiche Teile, verteile 7 dieser
Teile und zerlege das restliche Viertel in 7 gleiche Teile. Diese Zerlegung entspricht der
Formel
2
1
1
= +
;
2n − 1
n n(2n − 1)
man erhält so
1
1
2
1
1
2
= +
und
= +
.
5
3 15
7
4 28
Wir betrachten noch einmal die Aufgabe, natürliche Zahlen p, q ∈ N zu finden mit
2
1 1
= + .
n
p q
Setzen wir r := 2p und s := 2q, so erhalten wir
1
1
1
r+s
=
+
=
n
2p 2q
rs
oder
rs = n(r + s)
und damit
s=
nr − n2
n2
n2
nr
=
+
=n+
.
r−n
r−n
r−n
r−n
Also muss r − n eine Teiler von n2 sein. Wir untersuchen, welche Zerlegungen wir für
n = 15 erhalten. r − 15 muss ein Teiler von 225 sein. 225 hat die Teilermenge
T15 = {1, 3, 5, 9, 15, 25, 45, 75, 225} ;
also ergeben sich für r folgende Möglichkeiten:
r ∈ {16, 18, 20, 24, 30, 40, 60, 90, 240} .
1
Daraus erhalten wir 4 verschiedene Möglichkeiten,
als Summe von 2 verschiedenen
15
Stammbrüchen zu schreiben, nämlich
1
1
1
1
1
1
1
1
1
=
+
=
+
=
+
=
+
.
15
16 240
18 90
20 60
24 40
14
2
Daraus ergeben sich folgende Darstellungsmöglichkeiten für
als Summe von 2 verschie15
denen Stammbrüchen:
1
1
1
1
1
1
1
1
2
= +
= +
=
+
=
+
.
15
8 120
9 45
10 30
12 20
2
Ist n eine Primzahl, so gibt es genau eine Zerlegung von als Summe von zwei Stammn
brüchen.
Die meisten anderen Zerlegungen im Papyrus Rhind entsprechen nicht den oben angegebenen Formeln. Für n = 101 ist z.B.
◦
◦
◦
◦
2 : 101 = 101 202 303 606
angegeben, was man direkt aus der Zerlegung
2=1+
1 1 1
+ +
2 3 6
erhält.
In Problem 7 soll
2 ◦ ◦ 1
1
= 4 28= +
7
4 28
mit
◦ ◦
7
1 1
= 1 2 4= 1 + +
4
2 4
multipliziert werden. Wegen der Vorliebe für Stammbrüche werden die beiden Brüche in
2
der obigen Form als Summe geschrieben. Dann wird in der obigen Summendarstellung
7
7
(durch Erweitern mit 7) zu 28-teln gemacht und dann wird zweimal halbiert wegen =
4
1 1
1 + + , d.h.
2 4
1(Ganzes)
◦
2 (Hälfte)
◦
4 (Viertel)
Nun werden wegen
| 7
7
1
2
( =
+ )
7
28 28
| 1
◦
| 3 2
◦
1
31
1
( = 2 + 2 )
7
28 28
◦
1
1
13
(2 = 4 + 4 )
7
28 28
| 2
◦
◦
| 1 2 4 | 4
2 7
2
1 1
· = · (1 + + ) alle 28-tel addiert zu
7 4
7
2 4
◦
◦
◦
◦
◦
7 + 1 + 3+ 2 + 2 +1+ 2 + 4 + 4= 14
15
28-tel; wir erhalten
◦ ◦
◦ ◦
◦
4 28 · 1 2 4=2 .
In den nachfolgenden Aufgaben werden Flächenberechnungen und Volumenbestimmungen
durchgeführt. Problem 50 gibt die Anweisung zur Berechnung der Kreisfläche mit dem
Durchmesser d. Die Formel lautet
d
(d − )2
9
(=
64 2
64 2
d = 4·
·r ) ,
81 d=2r 81
was als Näherung von π den Wert
256
= 3.16....
81
ergibt. Wie kommt man darauf? Wenn man die Seite s eines Quadrats sucht, das den gleichen Flächeninhalt wie ein Kreis mit dem Durchmesser d hat, so denkt man bei Stammbrüchen an den Ansatz
1
1
s = d − · d = d(1 − )
n
n
und versucht (etwa durch Experimente) ein optimales n zu finden. n = 9 liefert optimale
Werte, n = 8 und n = 10 liefern schlechtere Ergebnisse.
Die Zahl π ist auch in den ägyptischen Pyramiden ”versteckt”. So haben fast alle Pyramiden den gleichen Böschungswinkel von ca. α = 510 520 . Es gibt nur zwei Pyramiden
mit anderen Böschungswinkeln, die sog. ”Knickpyramide” und die sog. ”stumpfe Pyramide” oder ”Rote Pyramide” bei dem Dorf Dahschur. Bei der Knickpyramide beträgt der
Böschungswinkel des oberen Teils und bei der stumpfen Pyramide der gesamte Böschungswinkel ca. β = 430 400 .
Knickpyramide
Stumpfe Pyramide
(entnommen aus [DiAr]). Wie kann man die beiden Winkel erklären? Rollt man eine
grosse Scheibe vom Radius r ab und ”stapelt” man dann 4 solcher Scheiben übereinander
(vgl. nachfolgendes Bild), so ergibt sich (mit unseren heutigen Kenntnissen)
tan α =
8r
4
=
2πr
π
16
oder
4
≈ 51.85390 .
π
Stapelt man dagegen nur 3 solcher Scheiben übereinander, so erhalten wir
α = arctan
tan β =
oder
β = arctan
6r
3
=
2πr
π
3
≈ 43.67920 .
π
Man findet häufig auch folgende Formulierung: Teilt man den Umfang der Pyramidenbasis (bei der Cheopspyramide 921,46 m) durch die doppelte Pyramidenhöhe (bei der
Cheopspyramide 293,46 m), so ergibt sich die Zahl 3.14 .
Nach 1500 scheint es in der Mathematik keine Fortschritte mehr gegeben zu haben; die
jünger datierten Funde (etwa aus dem 13. Jahrhundert) verlangen in ihren MathematikAufgaben keine größeren Kenntnisse als die großen Papyri.
c) Zahlzeichen der Griechen
Originale der Werke griechischer Mathematiker - wie der griechischen Schriftsteller überhaupt - sind nicht erhalten, mit Ausnahme einiger Papyri aus der Zeit um 200 n.Chr. (vgl.
Zeittafel, Folie 3, entnommen aus [TiL2] und [Ger1] bzw. [Ger3]). Sie sind aber besonders
wichtig, weil wir dadurch einen Einblick in das damalige Rechnen erhalten. Vollständige
Abschriften der Werke gibt es in der Philosophie erst von Platon, in der Mathematik erst
von Euklid an.
Für die Zahlenschreibung mit Individualzeichen gab es bei den Griechen 2 Systeme:
17
1) Die attische oder herodianische Schreibweise: Neben dem Einerstrich I werden für
die Zehnerstufen jeweils die Anfänge der betreffenden Zahlwörter benutzt; daneben
gibt es noch bei fünf eine Zwischenstufe, also (vgl. z.B. [Coll])
10 = ∆(für ’deka’) 100 = H(für ’hekaton’) 1000 = X 10000 = M
5 = Γ 50 = Γ∆
500 = ΓH
5000 = ΓX
50000 = ΓM
Beispiel :
4889 = XXXXΓH HHHΓ∆ ∆∆∆ΓIIII
Diese Zeichen lassen sich von 454 bis gegen 95 v.Chr. nachweisen.
2) Wesentlich kürzer, aber nicht so übersichtlich ist das jüngere System, das von ca.
450 v.Chr. an nachgewiesen ist. Es verwendet die 24 Buchstaben des Alphabets
zusammen mit 3 Sonderzeichen, also (vgl. [ReWe])
Die Tausender erhalten links einen kleinen Strich, z.B. 1000 =
ˆ 0 α; die Zehntausender
werden durch M (Zehntausend = eine Myriade) mit dem darüber gesetzten Zahlenfaktor
0
bezeichnet, z.B. 340000 = λδ
. Also erhalten wir 349450 = λδ
ϑυν. Manchmal wird zur
M
M
sorgfältigen Unterscheidung von den gewöhnlichen Buchstaben über den Zahlenbuchstaben ein Querstrich geschrieben.
Für astronomische Rechnungen verwendeten die Griechen das sexagesimale Zahlensystem,
das sie wahrscheinlich von den Babyloniern übernahmen. Man kann annehmen, dass bei
den Sexagesimalzahlen für die Leerstellen ein besonderes Zeichen benutzt wird: ein Omikron mit einem Strich darüber, z.B. O, o.
Die älteste überlieferte Handschrift mit einem Symbol für eine Sexagesimalnull datiert
allerdings erst aus dem 9. Jahrhundert n.Chr..
d) Zahlzeichen der Inder
Zu den ältesten Zahlzeichen in Indien zählen die sog. Kharosthi-Ziffern, bei denen sich
ein Dezimalsystem und ein Vierersystem überlagern. Man verwendet Individualzeichen
für 1 = |, 4 = X, 10 = 2, 20 = 3 und 100 = τ |. Belegt sind die folgenden Zahlzeichen, die
vom 4. bis zum 2. Jh. v.Chr. verwendet wurden:
1=|
2 = ||
3 = |||
4=X
5 = |X
6 = ||X
7 = |||X 8 = XX
10 = 2
20 = 3
30 = 23
40 = 33 50 = 233 60 = 333 70 = |333 80 = 3333
200 = τ || 300 = τ |||.
18
Neben diesen Ziffern wurden gleichzeitig auch die Brahmi-Ziffern (ab ca. 250 v.Chr.) mit
Individualzeichen für 1 und von 4 bis 9 benutzt (vgl. Folie 4, entnommen aus [Coll]).
Hieraus haben sich in Laufe der Zeit 9 Individualzeichen für die Ziffern 1 bis 9 sowie ein
Punkt oder ein kleiner Kreis für die Null entwickelt (vgl. Folie 5, entnommen aus [Trop]).
Aus dem 7. Jh. stammen Inschriften aus Südostasien, auf denen Ziffern im dezimalen
Positionssystem geschrieben sind mit einem Punkt oder einem kleinen Kreis für die Null.
Deshalb ist nicht eindeutig klar, ob das dezimale Positionssystem eine echte Erfindung
der Inder ist oder ob eine Entlehnung von anderer Seite (vielleicht chinesischer Seite)
angenommen werden muss. Ein Zeichen für die Null, nämlich ein Punkt, erscheint in China
erstmals in einem astronomisch-astrologischen Text aus der Zeit zwischen 718 und 729
n.Chr.. Eine Entlehnung des Zeichens für die Null von den Indern wird von chinesischen
Wissenschaftlern bestritten.
Die Kunde von dieser neuen (indischen) Art, Zahlen zu schreiben, drang auch nach Westen
vor. Im Jahr 662 schreibt der syrische Gelehrte Severus Sebocht: ” ... Ihre Zahlenschreibweise, die mit Hilfe von neun Zeichen vorgenommen wird, ist über jedes Lob erhaben”.
Entweder waren fehlende Potenzen durch Lücken angegeben, oder Severus zählte die Null
(als Kreis oder Punkt) nicht zu den Ziffern. Das bis heute älteste indische Zeugnis für die
Null (in Form eines kleinen Kreises) findet sich in einem kleinen Tempel in Gwalior in
Mittelindien, und geht auf das Jahr 870 n.Chr. zurück.
Die rasche Ausbreitung des Islams ab dem 7. Jh. und speziell die Handelsbeziehungen
der Araber bis hin nach Indien und China bewirkten, dass die indischen Zahlzeichen
allmählich die anderen Zahlensysteme verdrängten. Es ist bisher nicht gelungen, den Weg
der Null von Indien bis in die arabische Welt und dann weiter nach Europa lückenlos
zu verfolgen. Es gibt zwei Formen der Ziffernschreibweise, eine westarabische und eine
ostarabische. In der westarabischen Form sind diese Ziffern dann über Spanien ins übrige
Europa gekommen. Wenn wir heute von ”arabischen Ziffern” sprechen, meinen wir die
indisch-arabischen Ziffern in der westarabischen Form.
e) Der Weg der indisch-arabischen Ziffern nach Europa
Die älteste bekannte Verwendung der indisch-arabischen Ziffern (noch ohne die Null)
findet sich in einer Handschrift des nordspanischen Klosters Albeida aus dem Jahr 976.
Über Spanien (das Kalifat von Córdoba war bis 1236 das kulturelle Zentrum der maurischarabischen Welt, Granada fiel erst 1492 wieder an Kastilien) und Sizilien (von 878-1091
unter arabischer Herrschaft) gelangten die indisch-arabischen Ziffern einschliesslich der
Null nach Europa. Einen wesentlichen Beitrag zur Verwendung der neuen indischen Ziffern
leistete Leonardo von Pisa (Fibonacci = der Sohn des Bonaccio) (* 1170 (?) in Pisa, †1250
(?) in Pisa) durch sein Buch ”Liber abaci” aus dem Jahre 1202, in dem er dem Abacus
eine endgültige Absage erteilt und stattdessen das Rechnen mit den indisch-arabischen
Ziffern propagiert. Das ”Liber abaci” besteht aus 15 Kapiteln mit folgenden Inhalten:
Kap. 1-7:
Einführung der indisch-arabischen Ziffern und Methoden für das Rechnen mit ganzen Zahlen und mit Brüchen.
19
Kap. 8-11:
Probleme des kaufmännischen Rechnens. Als bemerkenswerte, spielerische Aufgabe
wird das ”Problem der Vögel” angeführt:
Ein Mann kauft 30 Vögel: Rebhühner, Tauben und Spatzen. Ein Rebhuhn kostet 3
Silbermünzen, eine Taube 2 und ein Spatz 1/2. Er bezahlt 30 Silbermünzen. Wieviele
Rebhühner, Tauben und Spatzen kann er kaufen?
Einzige ganzzahlige Lösung ist: 3 Rebhühner, 5 Tauben und 22 Spatzen.
Kap. 12-13:
Mehrere unterhaltsame Probleme, die auf eine lineare Gleichung oder auf Gleichungssysteme mit 2 oder 3 Unbekannten führen. Hier wird auch die FibonacciZahlenfolge eingeführt.
Kap. 14:
Rechnen mit Quadratwurzeln und Kubikwurzeln.
Kap. 15:
y
6
=
, x + y = 21
x
9
b) Anwendungen des Satzes von Pythagoras
c) Systematische Behandlung von linearen und quadratischen Gleichungen.
a) Gleichungen der folgenden Art
Noch im Jahre 1299 war den Geldwechslern von Florenz die Verwendung der indischarabischen Ziffern verboten, aber bereits 1338 bestanden in Florenz 6 Schulen zur Ausbildung der Kaufleute im Sinne der modernen Arithmetik.
Fibonacci hatte in seinem Buch von ”cephirum” gesprochen und dabei in lateinicher
Form das arabische Wort ”sifr”, das für ”Null; Nichts” steht, verwendet. Das deutsche
Wort ”Ziffer” kommt aus dieser arabischen Wurzel, wurde ursprünglich nur für die Null
benutzt und wurde später für sämtliche Zahlzeichen von 0 bis 9 verwendet. Wie lange es
gedauert hat, bis sich die moderne Schreibweise endgültig durchgesetzt hat, kann durch
folgende historisch belegten Beispiele gemischter Zahldarstellungen demonstriert werden:
1 · 5 · IIII
Cδ
I · O · V III · IX
IV 02
ICCOO
I · II · τ τ
1504
1104 (vgl. griechische Zahlzeichen)
1089
1502
1200
1200
(cifra wurde auf griechisch als τ ζιφ%α geschrieben, also Null mit dem Anfangsbuchstaben
τ bezeichnet.) An der Frauenkirche in München findet sich aus dem Jahr 1624 folgende
Mischform:
M · DC · Z4 .
Wie sich die indischen Ziffern im Abendland weiterentwickelt haben, kann man in Folie 6
(entnommen aus [Trop]) sehen.