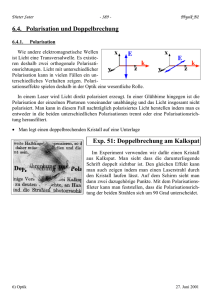
Kristalloptische Untersuchungen an Relaxor

Kristalloptische Untersuchungen an
Relaxor-Ferroelektrika
Diplomarbeit
zur Erlangung des akademischen Grades
Diplom-Physiker
vorgelegt von
Eric Beckers
Gerhard Mercator Universität Duisburg
Fachbereich 10
Angewandte Physik
April 2001
Inhaltsverzeichnis
1
EINLEITUNG ................................................................................................ 3
2
THEORETISCHE GRUNDLAGEN ............................................................. 4
2.1 FERROELEKTRIKA .......................................................................................... 4
2.2 FERROELEKTRISCHE RELAXOREN................................................................... 5
2.3 KRITISCHE EXPONENTEN ............................................................................... 7
2.4 STRONTIUM-BARIUM-NIOBAT........................................................................ 7
2.5 LINEARE DOPPELBRECHUNG .......................................................................... 9
2.6 DAS ZUFALLSFELD ISING MODELL ............................................................... 11
3
MEßMETHODEN UND EXPERIMENTELLE GRUNDLAGEN ............ 13
3.1 BABINET-SOLEIL-KOMPENSATION ............................................................... 13
3.2 SÉNARMONT-KOMPENSATION ...................................................................... 18
3.3 VERGLEICH DER BEIDEN MEßMETHODEN ...................................................... 23
3.4 PROBENPRÄPARATION ................................................................................. 26
3.5 PROGRAMMIERUNG DER STEUERUNG UND ÜBERSICHT DER KLASSEN DES
MEßPROGRAMMS ................................................................................................ 27
4
TEMPERATURABHÄNGIGKEIT DER LINEAREN
DOPPELBRECHUNG......................................................................................... 31
4.1 DEBYEKORREKTUR DER THERMISCHEN AUSDEHNUNG UND ORNSTEIN-ZERNIKE
NÄHERUNG ......................................................................................................... 31
5
HYSTERESEMESSUNGEN........................................................................ 42
5.1 DEHNUNGS- UND POLARISATIONSANTEIL DER DOPPELBRECHUNG ................ 42
6
FELDINDUZIERTE ZEITABHÄNGIGKEITEN DER LINEAREN
DOPPELBRECHUNG......................................................................................... 49
6.1 KURVENBESCHREIBUNG UND DARSTELLUNG DER MESSUNGEN ..................... 49
6.2 RELAXATION NACH FELDEINSCHALTEN ........................................................ 54
6.3 RELAXATION NACH FELDABSCHALTEN......................................................... 57
7
2
ZUSAMMENFASSUNG .............................................................................. 62
1 Einleitung
Das zur Familie der ferroelektrischen tetragonalen Wolfram-Bronzen gehörende
Material Sr0,61Ba0,39Nb2O6 (SBN) ist aufgrund seiner Eigenschaften im Bereich der
Pyroelektrizität1, der Elektrooptik2, der Akustooptik3, der Photorefraktivität4 und der
nichtlinearen Optik5 ein vielversprechendes Material für viele Bereiche der
Anwendung.
Das
SBN
ist
ein
uniaxiales
System
mit
ausgeprägten
Relaxoreigenschaften, welche sich mit dem Zufallsfeld-Ising-Modell6,7 (RFIM)
beschreiben lassen.8 SBN ist die erste experimentelle Realisation dieses
Modellsystems.
In dieser Arbeit wird die Auswirkung der Dotierung von SBN mit Chrom bzw.
Kobalt in Hinblick auf das Relaxorverhalten mit Hilfe der linearen Doppelbrechung
untersucht. Das Material SBN weist eine große bei lineare Doppelbrechung auf,
deshalb bieten sich hier Kompensationsmethoden nach Babinet-Soleil bzw.
Sénarmont an. Dabei wird gezeigt, daß sowohl Kobalt als auch Chrom, entgegen der
schon früher untersuchten mit Cer dotierten Proben,9 keinen Einfluß auf das
Zufallsfeldverhalten von SBN haben.
Feldinduzierte Relaxationen und Hysteresemessungen an einer mit Cer dotierten
Probe
zeigen
eine
breite
Domänengrößenverteilung
sowie
einen
großen
Dehnungsanteil in der gemessenen linearen Doppelbrechung. Die Hysteresekurven
weisen starke Verrundungen auf, was ein starkes Pinning der Domänen vermuten
läßt.
3
2 Theoretische Grundlagen
2.1 Ferroelektrika
Betrachtet man die 32 Punktsymmetrieklassen der Kristallgitter, so gibt es unter
ihnen 11, die ein Inversionszentrum besitzen. Diese haben keine polaren
Eigenschaften. Bei den restlichen 21 Punktsymmetrieklassen treten eine oder
mehrere polare Achsen auf. Bei Kristallen aus diesen Klassen bewirkt eine
mechanische Deformation eine Änderung der Polarisation. Andererseits bewirkt ein
angelegtes E-Feld eine Dehnung bzw. Stauchung des Kristalls.
Ein ferroelektrischer Kristall ist ein Spezialfall dieser Kristalle und besitzt
mindestens zwei Orientierungszustände. Er bildet Gebiete aus, in denen die
Polarisation jeweils dieselbe Richtung hat. Diese Gebiete nennt man Domänen.
Durch ein äußeres elektrisches Feld E läßt sich die Polarisation P der Domänen
umkehren. Die Polarisation ist also über die Suszeptibilität χ und die
Dielektrizitätskonstante ε0 mit dem elektrischen Feld verknüpft. Es gilt somit:
P = χε 0 E
(2.1.1)
Die Polarisation steigt mit wachsender Feldstärke an und läuft dann in eine
Sättigung PS. Nach Abschalten des Feldes verschwindet die Polarisation nicht völlig,
sondern es
bleibt die remanente Polarisation übrig. Diese kann erst durch ein
Gegenfeld, das Koerzitivfeld, beseitigt werden. Wie im magnetischen Fall spricht
man auch hier von Hysterese.
4
Abbildung 2.1.1: Ferroelektrische Hystereseschleife. Auf der x-Achse ist das
angelegte elektrische Feld aufgetragen, Ek ist die Koerzitivfeldstärke. Die yAchse zeigt die Polarisation pro Volumen. Der Achsenabschnitt entspricht der
remanenten Polarisation.
Oberhalb einer bestimmten Temperatur, der Curietemperatur, verschwindet diese
Eigenschaft. In Analogie zum Magnetismus spricht man hier vom paraelektrischen
Zustand, wobei hier der Unterschied besteht, daß im Magnetismus die Richtungen
der einzelnen Spins statistisch über den gesamten Körper verteilt sind und im Mittel
Null ergeben. Bei einem ferroelektrischen Körper hingegen verschwindet die
Polarisation völlig.
2.2 Ferroelektrische Relaxoren
Unter einem ferroelektrischen Relaxor versteht man ein ferroelektrisches
Material, welches die Eigenschaft hat, daß der Realteil der Dielektrizitätskonstante
im
Gegensatz
zu
herkömmlichen
ferroelektrischen
Kristallen
bei
der
Übergangstemperatur gerundet ist, also keine für einen Phasenübergang typische
Singularität besitzt. Desweiteren stellt man wie in Abbildung 2.2.1 zu sehen eine
starke Frequenzabhängigkeit des Peaks fest. Mit steigender Frequenz verschiebt sich
der Peak zu höheren Temperaturen. Der Phasenübergang wird durch diese
Eigenschaft
verschmiert
und
der
Kristall
behält
partiell
ferroelektrische
Eigenschaften bis in die paraelektrische Phase hinein. Ein typischer Vertreter der
Relaxoren ist PbMg1/3Nb2/3O3 (PMN)10.
5
5
100 Hz
1 kHz
5 kHz
10 kHz
25 kHz
50 kHz
100 kHz
250 kHz
500 kHz
1 MHz
2.5 MHz
5 MHz
10 MHz
4
4
χ' [10 ]
3
2
1
0
300
350
400
450
Temperatur [K]
Abbildung 2.2.1: Dielektrische Suszeptibilität von Sr0.61-xBa0.39Nb2O6:Ce
(x=0,0066)11. Die Frequenzabhängigkeit der Peaks sowie deren Rundungen sind
im Bild gut zu erkennen. Gemessen wurden Frequenzen im Bereich von 100 Hz
bis 10 MHz.
12
100 Hz
1 kHz
5 kHz
10 kHz
25 kHz
50 kHz
100 kHz
250 kHz
500 kHz
1 MHz
2.5 MHz
5 MHz
10 MHz
3
χ'' [10 ]
9
6
3
0
300
350
400
450
Temperatur [K]
Abbildung 2.2.2: Dielektrische Verluste der mit Cer dotierten SBN-Probe mit
x=0,0066.
6
2.3 Kritische Exponenten
Das Verhalten eines Phasenüberganges zweiter Art, wie er z.B. in Ferroelektrika
zu finden ist, läßt sich im kritischen Bereich oft durch Potenzgesetze seiner
thermodynamischen Funktion F beschreiben
F (t ) ∝ t ϕ
(2.3.1)
Hierbei ist t die reduzierte Temperatur t =
T − Tc
und ϕ der kritische Exponent.
Tc
Man sagt, ϕ verhält sich in der Umgebung des Phasenübeganges wie tϕ. Einige
wichtige kritische Exponenten sind in Tabelle 1 aufgeführt. Die kritischen
Exponenten weisen ein univerelles Verhalten auf und hängen nur von der Dimension
des Systems, der Reichweite der Teilchenwechselwirkungen und Spindimensionalität
ab. Mit dem letzten Punkt sind die relevanten Komponenten des Spins gemeint, oder
im ferroelektrischen Fall die Möglichkeiten der Polarisationsrichtungen.
Physikalische Eigenschaft
Kritischer Exponent
Wärmekapazität Cv
α
Ordnungsparameter
β
z.B. spontane Polarisation Ps
γ
Kompressibilität bzw.
Suszeptibilität χ
ν
Korrelationslänge
Tabelle 1: Einige thermodynamischen Funktionen und ihre kritischen
Exponenten.
2.4 Strontium-Barium-Niobat
Das
Material
Strontium-Barium-Niobat
in
der
Zusammensetzung
Sr0.61Ba0.39Nb2O6 (SBN) ist eine kongruent schmelzende Verbindung12. Dies hat den
Vorteil einer hohen Homogenität der Proben. Das SBN hat eine offene tetragonale
Wolfram-Bronze Struktur, auf deren Ecken Strontiumatome sitzen.
7
Abbildung 2.4.1: Schematische Darstellung der Einheitszelle von StrontiumBarium-Niobat (SBN)
Abbildung
(KZ)
12(Sr2+)
15(Sr2+ /Ba2+ )
2.4.2:
Koordinationszahlen
(KZ)
9(leer)
und
Darstellung
der
Besetzungsplätze der Typen A, B und C. Auf den Gitterplätzen vom Typ A mit
der Koordinationszahl 12 sitzen die Sr2+ Ionen, auf Typ B
mit
Koordinationszahl 15 Plätzen wahlweise Sr2+ oder Ba2+. Typ C Plätze mit der
Koordinationszahl 9 bleiben leer.
8
Die freien Gitterplätze vom Typ A werden ausschließlich von Strontiumatomen
besetzt, Typ B Gitterplätze wahlweise von Strontium oder Barium. Die Typ C Plätze
bleiben leer.
Die Niobionen befinden sich in der Mitte der Sauerstoffoktaeder und sind die
wesentlichen Träger der Polarisation in diesem System. In der paraelektrischen
Phase, in welcher der Kristall eine tetragonale Struktur besitzt (4/mmm), sitzen sie
genau in der Mitte der Oktaeder, in der ebenfalls tetragonalen ferroelektrischen
Phase (4mm) werden ca. 20% von ihnen entlang der polaren c-Achse ausgelenkt. Die
Größe der Auslenkung steigt mit der Abnahme der Temperatur. Die Auslenkung
erfolgt nur in c-Richtung, das System ist also uniaxial. Dies hat den Vorteil, daß es
sich relativ einfach beschreiben läßt, z.B. im Vergleich zu kubischen Systemen wie
PMN, bei dem die Polarisation in acht Richtungen stehen kann. Im Folgenden
können wir also zum Verständnis des Relaxors SBN mit Ising-Modellen arbeiten.
Wegen der Ladungsunordnung trifft das dreidimensionale Zufallsfeld-IsingModell zu. Die Zufallsfelder können aufgrund unterschiedlicher Ladungen
unterschiedlicher Dotierungen erreicht werden. Verwendet wurden Ce3+, Cr3+ und
Co2+ Dotierungen. Durch die nicht stöchiometrischen Ladungen entstehen Dipole,
welche ein lokales Feld aufbauen, dies ist das Zufallsfeld in unserem Modell. Diese
sind statistisch über den gesamten Kristall verteilt und polarisieren die Umgebung.
Im paraelektrischen bewirken die räumlichen Fluktuationen der lokalen Felder die
Ausbildung von polaren Clustern, welche beim Abkühlen die Bildung von kritisch
verlangsamten Nanodomänen unterstützen. Bei den Dotierungen mit Chrom werden
die Nb-Ionen substituiert. Daher besteht nun der Unterschied zur Cer-Dotierung, daß
der Abstand zum nächsten Polarisationsträger für Chrom viel größer ist und deshalb
der Einfluß darauf viel kleiner. Dies wird man bei den Messungen zur
temperaturabhängigen Doppelbrechung noch sehen.
2.5 Lineare Doppelbrechung
Das Phänomen Doppelbrechung tritt auf, wenn für das Licht, welches durch
einen nichtkubischen Kristall fällt, die Ausbreitungsgeschwindigkeit von seiner
Polarisation abhängt. Kristalle mit dieser Eigenschaft heißen optisch anisotrop, das
klassische Beispiel ist der Kalkspat.
Zur Erklärung des Effekts stelle man sich den eintretenden Lichtstrahl in zwei
Strahlen aufgeteilt vor, den ordentlichen (o-Strahl) und den außerordentlichen Strahl
9
(ao-Strahl). Die Polarisationen dieser beiden Strahlen stehen senkrecht aufeinander.
Die Ausbreitungsrichtung beider Strahlen hängen von der Orientierung des Kristalls
zum einfallenden Licht ab. Breiten sich beide Strahlen mit der gleichen
Geschwindigkeit aus, dann wird diese Richtung optische Achse genannt. In dieser
Eintrittsrichtung verhält sich das Material wie ein isotroper Körper. In jeder anderen
Richtung trennen sich der ordentliche und der außerordentliche Strahl und verfolgen
unterschiedliche Ausbreitungsrichtungen durch den Kristall. Demzufolge sind auch
die Austrittspunkte beider Strahlen verschieden.
Abbildung 2.5.1: Strahlengang durch einen doppelbrechenden Kristall. Der
ordentliche
Strahl
ist
senkrecht
zur
Zeichenebene
polarisiert,
der
außerordentliche Parallel dazu. Die gestrichelten Linien zeigen die Lage der
optischen Achse.
r
r
Die elektrische Verschiebungsdichte D ist eine Funktion des elektrischen Feldes E
r
und der Polarisation P .
r
r
D = εε 0 E
(2.5.1)
Hierbei ist ε der Dielektrizitätstensor. Dieser hat in diagonalisierter Form die Gestalt:
 ε1 0

ε =  0 ε2
0 0

0

0
ε 3 
(2.5.2)
Vernachlässigt man die Absorption des Kristalls und setzt den Permeabilitätstensor
µ≈1, was für Frequenzen im optischen Bereich zutrifft, so ergibt sich für die
Hauptbrechungsindizes ni:
10
ni = ε i
(2.5.3)
Hierbei
ist
i=1,2,3
und
entspricht
den
drei
Raumrichtungen.
Die
drei
Brechungsindizes spannen einen Ellipsoid auf, welcher durch die Gleichung (1.5.4)
beschrieben wird.
x12 x22 x32
+
+
=1
n12 n22 n32
(2.5.4)
Dieser Ellipsoid wird auch Indikatrix genannt und beschreibt die Lichtausbreitung im
Kristall.
2.6 Das Zufallsfeld Ising Modell
Das Zufallsfeld Ising Modell (engl. random-field Ising Model, RFIM) wurde das
erste Mal von Imry und Ma vorgestellt.6 Hierbei sieht die Hamiltonfunktion
folgendermaßen aus:
H = − J ∑ si s j − ∑ hi si
ij
(2.6.1)
i
Der erste Anteil drückt die Austauschwechselwirkung der Spinvariablen si und sj
aus. Im ferroelektrischen Fall entspricht dies der Wechselwirkung von Dipolen. Der
Wert J ist eine Austauschkonstante. Der zweite Anteil entspricht der ZeemanEnergie der Spinvariablen si mit stochastisch verteilten Feldern. Für diese
Zufallsfelder gilt:
hi = 0
(2.6.2)
d.h. die Felder sind im Mittel gleich Null. Es liegen also genausoviele Spins in up
Richtung wie in down Richtung vor. Weiterhin gilt, daß das mittlere Zufallsfeld nicht
gleich Null ist
hi2
1/ 2
≠ 0.
(2.6.3)
Zur Beschreibung der Verteilung der Zufallsfelder werden in der Regel Gaußoder bimodale Verteilungen angesetzt.
Stellt man nun den Energiegewinn durch Bildung von Domänen dem
Energieverlust durch die Wandenergie gegenüber, so sieht man, daß die kritische
11
Dimension für das Random Field Ising Modell d=2 ist13. Für d>2 ist das System also
stabil und eine vorliegende Fernordnung wird durch die Zufallsfelder nicht gestört.
12
3 Meßmethoden und experimentelle Grundlagen
Zur
Messung
der
linearen
Doppelbrechung
werden
gerne
Kompensationsmethoden verwendet. Dabei wird der durch eine doppelbrechende
Probe, in unserem Fall das SBN, auftretende Brechungsindexunterschied durch ein
anderes Bauteil ausgeglichen, so daß im gesamten Aufbau keine Differenz mehr
auftritt. Hier sollen zwei dieser Aufbauten beschrieben werden, welche auch bei den
Messungen zum Einsatz kamen. Die erste ist die Babinet-Soleil-Kompensation, bei
der zum Ausgleich der auftretenden Doppelbrechung ein System aus Quarzkeilen
benutzt wird, welche im nächsten Kapitel genauer erklärt werden sollen. Bei der
zweiten Methode, der Sénarmont-Kompensation wird der Quarzkeil durch einen
rotierenden Analysator und ein λ/4-Plättchen ersetzt.
3.1 Babinet-Soleil-Kompensation
Bei der Babinet-Soleil-Kompensation besteht der Aufbau wie in Abbildung 3.1.1
gezeigt aus einer von einem Trafo der Firma Leitz betriebenen Natriumdampflampe
von OSRAM, deren Licht der Wellenlänge λ=589,3nm durch einen Polarisator
fällt14. Die Natriumdampflampe hat gegenüber einem Laser den Vorteil, daß ihr
Licht nicht kohärent ist. Weiterhin ist ihr Licht hinreichend monochromatisch. Das
nun linear polarisierte Licht fällt auf den Babinet-Soleil Kompensator, welcher sich
in einem Winkel von 45° zum Polarisator befindet. Dieser besteht aus einer
Quarzplatte und zwei Quarzkeilen, welche über einen Schrittmotor gegeneinander
verschoben werden können. Die n2-Achsen der beiden Keile sind parallel zueinander,
aber senkrecht zur Richtung der n2-Achse der Quarzplatte.
13
Abbildung 3.1.1: Aufbauskizze der Babinet-Soleil-Kompensation.14 Neben einer
Skizze des Aufbaus ist ganz rechts die Polarisation des Lichts beim
Durchqueren des Meßaufbaus zu sehen.
14
Sowohl die planparallele Platte als auch die beiden Keile verursachen eine
Phasendifferenz ∆ϕ1 (Platte) bzw. ∆ϕ2 (Keile), welche vom durchlaufenen Lichtweg
abhängt. Im Falle der Platte entspricht dies genau ihrer Dicke dk1, im Falle der Keile
ist die durchlaufene Dicke dk2 von der Verschiebung der Keile gegeneinander und
somit von der durch den Schrittmotor gefahrenen Schritte S abhängig.
∆ϕ1 =
2π
d k 1 (n2 − n1 )
λ
(3.1.1)
2π
d k 2 (S )(n2 − n1 )
λ
(3.1.2)
und
∆ϕ 2 =
Die Dicke dk2 erhält man über die Beziehung:
d k 2 ( S ) = d k1 +
λ
S
n2 − n1 S 0
(3.1.3)
Abbildung 3.1.2: Der Doppelkeil nach Babinet-Soleil besteht aus einer
doppelbrechenden Platte, auf der zwei doppelbrechende Keile gegeneinander
verschoben werden können. Der obere Keil in der Abbildung wird hierbei in
Richtung S bewegt. Die Achse n2 liegt für die Platte in der Zeichenebene, die n2
Achse der beiden Keile steht senkrecht dazu. Dadurch ist gewährleistet, daß bei
genau übereinanderliegenden Keilen die Doppelbrechung des Aufbaus
verschwindet.14
Der Wert S0 ist hierbei die Schrittzahl, welche für eine Phasendifferenz von 2π
notwendig ist. Sie ist wellenlängenabhängig und beträgt für die verwendete
Natriumdampflampe S0=30996. Für die Phasendifferenz ∆ϕk=∆ϕ1+∆ϕ2 des
Kompensators ergibt sich also:
15
∆ϕ k =
2π
S
(d k1 − d k 2 (S ))(n2 − n1 ) = −2π
S0
λ
(3.1.4)
Das Licht durchquert nun die doppelbrechende Probe der Dicke dp, welche ebenfalls
eine Phasendifferenz ∆ϕp verursacht.
∆ϕ p =
2π
d p ∆nac
λ
(3.1.5)
Hierbei ist ∆nac=na-nc die Doppelbrechung.
Der Kompensator wird im Folgenden immer so abgeglichen, daß die
Phasendifferenz der Probe genau ausgeglichen wird. Für die Phasendifferenzen der
Probe ∆ϕP und des Kompensators ∆ϕk gilt also folgende Bedingung:
∆ϕ k + ∆ϕ p = 0
(3.1.6)
Durch den nun folgenden Analysator, der genau im rechten Winkel zum Polarisator
steht, sollte also im Idealfall kein Licht mehr kommen. Der bis hierher nicht
erwähnte elasto-optische Modulator hat die Aufgabe, die Polarisation des Lichtes mit
einer Frequenz ωMod von ca. 50kHz zu modulieren. Er besteht aus einen
Quarzquader.
Abbildung 3.1.3: Skizze des elastooptischen Modulators. Die Dicke ist mit dm
bezeichnet, die Länge mit l.
Dies wird dadurch erreicht, daß der Kristall mit dieser Frequenz gedehnt bzw.
gestaucht wird. Diese Dickenänderung hat eine Änderung der Doppelbrechung zur
Folge, weil die Doppelbrechung ∆nMod proportional zur elastischen Spannung σ ist.
Die elastische Spannung wiederum ist proportional zur Ableitung der Auslenkung p
nach dem Ort.
∆nMod ∝ σ ∝
16
∂p
2π
 2π 
= p0
cos  sin (ω Mod t )
∂x
λ
 λ 
(3.1.7)
Das benutzte Modulationssignal dient als Referenzfrequenz für den Lock-In
Verstärker von EG&G. Setzt man nun die Phasendifferenz des Kompensators und
die der Probe über die Kompensationsbedingung in Relation, so ergibt sich eine
Formel für die gemessene Doppelbrechung ∆nac.
∆nac =
S λ
S0 d p
(3.1.8)
Für eine genauere Beschreibung des Meßverfahrens, welches die Intensität des
verwendeten Lichtes untersucht, wird hier auf Kapitel 3.2 verwiesen. Dieses Kapitel
beschreibt die andere verwendete Meßmethode nach Sénarmont und die verwendeten
Geräte.
17
3.2 Sénarmont-Kompensation
Photomultiplier
Hochspannungsquelle
für den Photomultiplier
Schrittmotor
Analysator
Lambda/4
50 KHz Oszillatorquelle
Computer
Heiztisch
Lock-In
Modulator
Polarisator
Signalanpassung
Lampe
Hochspannungsquelle
für feldabhängige
Messungen
Schrittmotorsteuerung
Voltmeter
Abbildung 3.2.1: Skizze des Versuchsaufbaus nach Sénarmont. Der Weg des
Natriumlichtes durch die verschiedenen Bauteile Polarisator, Modulator,
Heiztisch, Lambda/4-Platte und Analysator ist links zu sehen. Der Computer ist
der zentrale Bestandteil des Aufbaus. Einerseits kontrolliert er die Steuerung
des Schrittmotors und regelt die Temperatur des Heiztisches der Firma Linkam
über die mitgelieferten Geräte LNP und TP93. Andererseits liest er das aktuelle
Signal am Lock-In Verstärker aus.
In der Abbildung 3.2.1 ist das Blockschaltbild unserer Apparatur in
abgewandelter Form nach Sénarmont dargestellt.
Bei der Sénarmont-Kompensation wird der Doppelkeil durch zwei andere
Elemente ersetzt, ein λ/4-Plättchen (Q) und einem rotierenden Analysator (A). Auch
hier wird das Licht der Natriumdampflampe als erstes durch den Polarisator (P)
geschickt und durchläuft danach den Modulator (M). Nun wird der durch die Probe
(S) auftretende Phasenunterschied nicht durch einen Doppelkeilaufbau korrigiert,
18
sondern das Licht wird weiter durch ein λ/4-Plättchen und durch den rotierenden
Analysator geleitet15.
Abbildung
3.2.2:
Polarisationsrichtungen
der
einzelnen
Elemente
im
Sénarmontaufbau.
Bei der Sénarmont-Kompensation wird genau wie bei der Babinet-SoleilKompensation das den Aufbau durchquerende Licht immer auf Null geregelt. Die
Bedingung hierfür kann man sich mit Hilfe des Jones-Matrizenformalismus16
herleiten. Dabei wird die Wirkung jeder Komponente des Aufbaus auf
durchlaufendes Licht mit den Feldkomponenten Ex und Ey durch eine Matrix
beschrieben.
r
r
Ee = A × Q × S × M × P × Ea
(3.2.1)
Hierbei sind:
0 0
 cos( ρ / 2) i sin( ρ / 2) 
 cos ² β
 M = 
 A = 
P = 
0 1
 i sin( ρ / 2) cos( ρ / 2) 
 cos β sin β
 Ex 
 i 0
 cos(ϕ / 2) i sin(ϕ / 2) 
 S = 

E a =   Q = 
E
0
1
i
sin(
ϕ
/
2
)
cos(
ϕ
/
2
)
y




 
cos β sin β 

sin ² β 
(3.2.2)
Der Polarisator P ist so vorgegeben, daß ihn nur der y-Anteil des eingestrahlten
Lichts passieren kann. Wendet man nun noch die Matrix M des Modulators an, so
ergibt sich an dieser Stelle eine Formel:
r
 iE sin
Ee = A × Q × S ×  y
 E y cos
( )
( )
ρ
2
ρ
2
(3.2.3)
Als nächstes durchläuft das Licht die Probe S. Die Multiplikation mit dieser Matrix
ergibt:
 iE sin
= A × Q ×  y
 E y sin
( )cos( ) + iE cos( )sin ( )
( )sin ( ) + E cos( )cos( ) 
ρ
2
ρ
2
ϕ
2
ϕ
2
ρ
2
y
y
ρ
2
ϕ
2
ϕ
2
(3.2.4)
19
An dieser Stelle kann die Formel mit Hilfe von Sinus bzw. Cosinussatz vereinfacht
werden. Wendet man dann noch die Matrix für das λ/4-Plättchen an so folgt:
( )
( ) 
 − E y sin ρ +2 ϕ
= A× 
 E cos ρ +ϕ
2
 y
(3.2.5)
Insgesamt ergibt sich für das E-Feld des Licht nach Durchlaufen aller Komponenten:
r
ρ + ϕ  cos β 


Ee = E y sin  β −

2  sin β 

(3.2.6)
Gemessen wird jetzt aber nicht das E-Feld, sondern die Intensität des Lichts. Deshalb
muß die Formel noch quadriert werden.
r
I ∝ Ee
( )
2
ρ +ϕ 

= E y2 sin 2  β −

2 

(3.2.7)
Ersetzt man den sin²-Term durch einen Cosinusausdruck und setzt für den Modulator
ρ=ρ0sin(ωt)14 ein, so erhält man den folgenden Ausdruck:
I ∝ 12 E y2 [1 − cos(2 β − ( ρ 0 sin(ωt ) + ϕ ))]
(3.2.8)
Löst man den Cosinusausdruck noch auf ergibt sich eine Formel, in dem
verschachtelte Funktionen auftreten.
I ∝ 12 E y2 [1 − cos(2 β − ϕ )cos( ρ 0 sin(ωt )) + sin (2 β − ϕ )sin ( ρ 0 sin(ωt ))]
(3.2.9)
Die verschachtelten Funktionen können aufgelöst werden, wenn man die
Funktion in eine Fourierreihe entwickelt. Dadurch ergibt sich ein Ausdruck für die
Intensität des verwendeten Lichts und einer für die Intensität des Lichts mit der
doppelten Frequenz. Hierbei sind die Vorfaktoren Besselfunktionen.
I ω ∝ 12 J 1 ( ρ 0 ) sin (ϕ − 2 β )
(3.2.10)
I 2ω ∝ 12 J 2 ( ρ 0 ) cos(ϕ − 2 β )
(3.2.11)
Man sieht hier, daß die Intensität in der ersten Formel auf Null geht, wenn der
Sinus Null wird, bei der zweiten ist es der Cosinus. Da in beiden Fällen die
Argumente gleich sind, ist die Intensität des einen Anteils immer maximal, wenn der
andere minimal ist und umgekehrt. Bei unserer Meßmethode gleichen wir das Signal
20
immer auf Null ab. Als Kompensationsbedingung ergibt sich also für Iω=0 für
Gleichung (3.2.10):
ϕ
=β
2
(3.2.12)
Man hat nun noch die Möglichkeit, das Meßsignal über die Amplitude des
Modulatorsignals zu maximieren, welche das Argument der Besselfunktion ist. Wie
in der Abbildung zu erkennen, liegt das Maximum der ersten Besselfunktion bei
105°.
Abbildung 3.2.3: Die ersten beiden Besselfunktionen. Die Einstellung des
Maximums der ersten Besselfunktion liefert für das Meßsignal den
größtmöglichen Wert.
Die Phasendifferenz der Probe und die Phasendifferenz des Kompensators bzw.
die Abgleichbedingung für den Schrittmotor sind beide schon aus dem Abschnitt
über die Babinet-Soleil-Kompensation bekannt und stehen in den Gleichungen
(3.1.4) und (3.1.5):
β = ∆ϕ k =
S
2π
S0
(3.2.13)
und
∆ϕ p =
2πd
∆n
λ
(3.2.14)
Hieraus ergibt sich unter Verwendung der oben hergeleiteten Abgleichbedingung:
∆n = 2
S λ
S0 d
(3.2.15)
21
Das S0 ist an dieser Stelle ein anderes als das, welches bei Babinet-Soleil
vorliegt. Es muß erst neu bestimmt werden. Es entspricht genau dem Unterschied in
der Phase von 2π, in unserem Fall ergab sich S0=12048.
Bei der Umsetzung des neuen Programmes wurde der Aufbau in der Weise
geändert, daß auf das Gerät verzichtet werden konnte, welches vorher den Abgleich
des Schrittmotors und das Einlesen der Signale übernommen hatte. Der sogenannte
Rödler wird nun durch eine Interfacekarte ersetzt, welche im PC eingebaut ist. Diese
übernimmt das Einlesen der Lock-In Signale, die Steuerung des Schrittmotors und
die Steuerung der Spannung für die feldabhängigen Doppelbrechungsänderungen der
Messungen. Für die Ansteuerung des Schrittmotors war eine kleine Schaltung nötig.
Eine Skizze des Bestückungsplans ist in Abbildung 3.2.4 zu sehen.
25
1
Ca3130
Modul
Netzteil
7406
7406
LM7805
25
1
Abbildung 3.2.4: Bestückungsplan der Signalanpassung.
22
3.3 Vergleich der beiden Meßmethoden
Die Sénarmont-Kompensation hat gegenüber der Babinet-Soleil-Kompensation
aufgrund des rotierenden Analysators den Vorteil, daß man die Möglichkeit hat,
Kurven ohne Unterbrechung durchzumessen. Der Doppelkeil des Babinet-SoleilKompensators besitzt nur einen begrenzten Laufweg, nach dem er wieder
zurückgestellt werden muß und damit eine neue Messung beginnt. Die einzelnen
Messungen müssen dann zusammengesetzt werden. Dies spielt vor allem bei Proben
mit großer Doppelbrechungsänderung eine Rolle, wie im Falle von SBN. Um einen
Vergleich der Genauigkeit der Meßmethoden zu haben, wurde mit beiden eine
kristalline Quarzprobe über einen Temperaturbereich von 330K bis 360K gemessen.
Dieser Bereich hat zwei Vorteile. Erstens liegt der Temperaturbereich hoch genug,
daß eine Regelung der Temperatur für den Heiztisch ohne Stickstoff möglich ist. In
der Nähe der Zimmertemperatur würde die Regelung je nach Bedarf die
Stickstoffkühlung abschalten bzw. zuschalten. Dies hätte stärkere Schwankungen zur
Folge. Zweitens ist die Doppelbrechungsänderung mit der Temperatur in diesem
Gebiet nahezu linear und die relativen Änderungen sehr klein. Sie liegen im Bereich
von ∆n≈10-6. In diesem Bereich wird auch die Grenze der Genauigkeit für die
Sénarmontkompensation ohne Modulator vermutet17. Die gemessenen Kurven sind
in Abbildung 3.3.1 zu sehen.
23
8,0x10
-5
6,0x10
-5
4,0x10
-5
2,0x10
-5
∆n
Senarmont
Babinet-Soleil
0,0
330
335
340
345
350
355
360
365
370
375
Temperatur [K]
Abbildung 3.3.1: Messung der Doppelbrechung von Quarz mit Sénarmont- bzw.
und Babinet-Soleil-Kompensator. Bei der Babinet-Soleil Messung ist deutlich
eine Modulation des Signals zu erkennen.
Bei der Babinet-Soleil Kompensation ist deutlich eine periodische Modulation
des Meßsignals zu erkennen. Diese Verfälschung der Messung wird vermutlich
durch den planparallelen Doppelkeil des Kompensators hervorgerufen. Das Licht
wird am Übergang Quarz-Luft, also beim Verlassen des Kompensators, zum Teil
reflektiert. Das Gleiche passiert ebenso mit dem reflektierten Licht beim Übergang
Quarz-Luft auf der anderen Seite des Kompensators. Insgesamt wird das Signal also
durch die entstehenden Interferenzstreifen verfälscht. Dies ist in Abbildung 3.3.2
skizziert.
24
Licht
Babinet-Soleil
Kompensator
Abbildung 3.3.2: Meßsignalverfälschung durch Reflexionseffekte am BabinetSoleil-Kompensator
Entspricht die Dicke des Doppelkeils einem Vielfachen der Wellenlänge des
Lichts, addiert sich das Licht wieder zum eigentlichen Strahl hinzu und das Signal
ändert sich nur durch das Licht, welches den Aufbau verlassen kann, also
Verlustlicht. Bei einer anderen Dicke hingegen kann es sogar zu einer maximalen
Auslöschung kommen, wobei die Null, auf welcher abgeglichen wird, eher erreicht
wird. Der gesamte Effekt ist damit also abhängig von der Wellenlänge des
verwendeten Lichts und kann in der Modulation wiedergefunden werden. Die höhere
Genauigkeit der Sénarmont-Kompensation ist nicht überraschend. In beiden
Aufbauten werden die gleichen Komponenten benutzt, so ist z. B. der Analysator,
welcher wahrscheinlich im Sénarmontaufbau den größten Fehler verursacht, ebenso
im Babinet-Soleil Aufbau vorhanden. Dort kann also kein Unterschied vorliegen. Es
gibt nur 2 Bauteile, welche im einen Aufbau auftreten und im anderen nicht. Im
Babinet-Soleil Aufbau ist es der oben erwähnte Doppelkeil, im Sénarmontaufbau ist
es das λ/4-Plättchen. Zu vergleichen wären also diese beiden Komponenten, wobei
das λ/4-Plättchen schon von seiner einfachen Bauweise im Vorteil ist. In der
Abbildung 3.3.1 sind noch eine lineare Anpassung an die gemessenen Werte zu
sehen. Die Standardabweichungen für diese Kurven findet man in Tabelle 2. Wie
man dort sieht, haben die Anpassungen unterschiedliche Steigungen. Dies kommt
daher, daß bei der Babinet-Soleil-Kompensation kein kompletter Durchlauf von 2π
gemessen wurde, welcher den Einfluß der Modulation auf die Steigung ausschließen
25
würde. Weiterhin stellt man anhand der Standardabweichung eine Steigerung der
Güte der Messung um den Faktor 10 fest.
Die Meßmethode nach Sénarmont bietet also sowohl eine Vereinfachung der
Messungen als auch eine höhere Genauigkeit.
A
B
SD
(Standarabweichung)
Sénarmont
Babinet-Soleil
-3,1⋅10-4 ±1,1⋅10-7 1,0⋅10-6 ±3,2⋅10-10
1,4⋅10-7
-5,1⋅10-4 ±1,8⋅10-6
1,9⋅10-6
1,5⋅10-6 ±5,1⋅10-9
Tabelle 2: Parameter der linearen Anpassungen der beiden gemessenen Kurven
aus Abbildung 3.3.1.
3.4 Probenpräparation
Die benutzten SBN-Proben wurden uns von Herrn Dr. Rainer Pankrath von der
Universität Osnabrück zur Verfügung gestellt und von Herrn Dr. Theo Woike,
Universität zu Köln, geschnitten und poliert. Diese hatten alle den für die lineare
Doppelbrechung nötigen a-Schnitt, d.h. daß die c-Achse in der Ebene des Schnittes
liegt. Die Proben hatten im Durchschnitt eine Dicke von 1mm, was zur Folge hat,
daß der doppelbrechende Effekt für SBN mit seinen großen Brechungsindexunterschieden18,19 genügend groß ist. Die genauen Abmessungen der
untersuchten Proben stehen in Tabelle 3.
Dotierung
Dicke/mm
Kantenlänge
Kantenlänge
Parallel c/mm
Senkrecht c/mm
Ce 0,0066
1,07
6,6
6,6
Co 0,0002
1,3
7,7
7,1
Cr 0,003
1,80
6
6,1
Cr 0,006
0,92
5,1
5,7
Cr 0,015
0,486
6,4
5,0
Tabelle 3: Abmessungen der verwendeten Cer, Chrom und Kobalt dotierten
SBN Proben.
Die Proben wurden vor Gebrauch mit Hilfe des Heiztisches auf Temperaturen
über 800K erhitzt und auf diesem Wert für mindestens eine Stunde gehalten um das
Gedächtnis des Materials zu löschen. Eine andere Möglichkeit besteht darin, die
26
Probe in Öl auf 500K zu erhitzen, was aber den Nachteil hat, daß die Probe nach
diesem Vorgang gereinigt werden muß. Bis sie in den Heiztisch eingesetzt werden
kann, ist sie somit auf Temperaturen unterhalb von Tc gebracht worden. Für die
Untersuchung
mit
elektrischen
Feld,
Relaxations-
bzw.
feldabhängige
Doppelbrechungsänderungen, mußte die Probe kontaktiert werden. Für die
Elektroden wurde Leitsilber benutzt. Danach konnten dünne Drähte durch einen
kleinen zusätzlichen Tropfen Leitsilber an der Probe befestigt werden. Durch einen
nachträglich
am
Heiztisch
angebrachten
Anschluß
konnte
über
eine
Hochspannungsquelle der Firma Canberra Model 3002 die Probe mit einer Spannung
zwischen 0 und 550V versorgt werden. Um einen definierten Startpunkt bei den
Relaxationsmessungen zu haben, wurde das bisherige Meßprogramm so modifiziert,
daß ein Feld angelegt bzw. abgeschaltet werden.
3.5 Programmierung der Steuerung und Übersicht der
Klassen des Meßprogramms
Für die Messung der Doppelbrechung sollte ein neues Programm mit graphischer
Benutzeroberfläche mit Hilfe von Visual C++ entwickelt werden. Zur Steuerung der
Messung wurden verschiedene Programmteile benötigt, bei denen die Wichtigsten
die Schrittmotorsteuerung, die Aufnahme der Lock-In Signale und die Regelung der
Probenspannung waren. Weiterhin gibt es Routinen für die Speicherung und das
Einlesen von Messdaten, automatische Skalierung und eine Abfragefunktion für die
Temperatur, welche auch programmabhängig nach Bedarf
gesteuert wird. Die
programmierten Klassen, dazugehörigen Funktionen und benutzte Variablen werden
in der Abbildung 3.5.1 und Abbildung 3.5.2 gezeigt. Für die Funktion „Punkt“,
welche dazu dient, eine temperaturabhängige Doppelbrechungskurve aufzunehmen,
wurde ein Nassi-Schneiderman Diagramm erstellt. Dieses ist in Abbildung 3.5.3 zu
sehen. Anhand dieser Funktion kann der wesentliche Teil einer Messung erkannt und
nachvollzogen werden. Dies soll als Beispiel für das Meßprogramm dienen. In den
ersten Punkten werden die Grundeinstellungen der seriellen Schnittstelle wie
Baudrate und Bitzahl festgelegt und die vorgewählte Temperatur angefahren. Danach
wird beim Erreichen der Starttemperatur auf eine Bestätigung des Messstarts
gewartet. Dies hat den Vorteil, daß man den Startpunkt dann wählen kann, wenn die
Probe
einige
Zeit
auf
diesem
Wert
gehalten
wurde
und
somit
keine
Temperaturgradienten vorliegen. Im eigentlichen Meßablauf wird der Lock-In-Wert
27
eingelesen und über den Schrittmotor wieder auf Null geregelt. Nach einer
angemessenen Wartezeit, die wiederum eine Temperaturrelaxation der Probe
gewährleisten soll, wird der Wert erneut eingelesen und gegebenenfalls erneut
korrigiert. Dies wird mit unterschiedlich langen Pausen wiederholt. Nachdem der
Wert dann aufgenommen und gespeichert wurde, wird die ganze Prozedur
wiederholt, bis die Endtemperatur erreicht ist.
Globales
Grundeinstellungen
Datenkopie
T2
MessAD
Anhalten
Tempo
MessDA
Fein
Zeitkonstante
Pause
LINKS
RateEinstellen
RECHTS
SendePause
Programm
SFahren
Rate
Temperatureinstellen
SCHZahl
Temperaturholen
T1
Abbildung 3.5.1: Globale Variablen (einfache Kästchen) und Funktionen (3D
Kästchen) des Meßprogramms.
28
CFenster
CMessdaten
Autoskalierung
Anzeigen
CMessdaten
Messprog
DateiOeffnen
Bereich
Messung
Temperatur
DateiSpeichern
Darstellung
Messungstarten
DatensatzLoeschen
Kommentar
OnKeyDown
DatenSichern
Maximum
Punkt
Grenzen
MaxMin
Tempanzeige
MaxSuchen
Minimum
WerteEinstellen
MinSuchen
pStandardMenu
OnPaint
StatusBar
WerteUmwandeln
CGrenzenDialog
CMessProgramm
CGrenzenDialog
MaxX
OnCancel
MessRate
OnInitDialog
MaxY
OnInitDialog
Temp1
OnOK
MinX
OnOK
Temp2
MinY
Werte
CTemp
CBasisDialog
CTemp
OnInitDialog
Temperatur
CBasisDialog
Geschwindigkeit
OnInitDialog
Zeitk
OnOK
Genau
CAnwendung
InitInstance
Abbildung 3.5.2: Die sieben Klassen des Meßprogramms.
29
Grundeinstellungen der seriellen Schnittstelle
Startwert der Temperatur anfahren, Wert halten
Beim Erreichen der Temperatur Messstart bestätigen
Endwert der Temperatur einstellen, Wert halten
Meßwert des Lock-Ins größer als die vorgewählte Genauigkeit
Schrittmotor nachregeln
Meßwert des Lock-Ins kleiner als die vorgewählte Genauigkeit
Schrittmotor nachregeln
3 Sekunden warten
Hat sich das Meßsignal noch geändert?
2 min warten
Hat sich das Meßsignal noch geändert?
Ausgabe des gemessenen Wertes und speichern
Hochheizen bis zum nächsten Wert
Nächster Temperaturwert erreicht?
1 Sekunde warten
Neuen Temperaturwert holen
Abbruch bei drücken der Leertaste oder beim Erreichen der Endtemperatur
Abbildung 3.5.3: Nassi-Schneiderman Diagramm für die Funktion „Punkt“. Die
einzelnen Programmschritte sitzen in den einzelnen Kästchen. Bei einer Lförmigen Struktur handelt es sich um eine Schleife, wobei unten die
Abbruchbedingung steht.
30
4 Temperaturabhängigkeit der linearen Doppelbrechung
4.1 Debyekorrektur
der
thermischen
Ausdehnung
und
Ornstein-Zernike Näherung
Bei der Untersuchung der Temperaturabhängigkeit wurden mit Chrom dotierte
Proben gemessen. Die Dotierungen hierbei waren x=0,003, x=0,006 und x=0,015.
Gemessen
wurde
mit
der
Babinet-Soleil
Kompensation
über
einen
Temperaturbereich von ca. 80K-850K. Die Temperaturdifferenz zwischen den
einzelnen Punkten wurde von 0,5K/min in den Randbereichen hoher bzw. niedriger
Temperatur auf 0,1K/min in der Umgebung des Phasenüberganges geändert. Dies ist
die Grenze der Genauigkeit des Heiztisches von Linkam.
10 (∆nac-∆nac(80K))
5
6
th
∆nac
2
4
2
3
2
1
2
2
th
10 |∆nac-∆nac |
4
8
0
SBN:Co
(x=0,0002)
0
200
400
600
800
Temperatur [K]
1
0
100
200
300
400
500
600
700
800
Temperatur [K]
Abbildung 4.1.1: Kurvenverlauf der Doppelbrechung am Beispiel einer mit
Kobalt dotierten SBN Probe mit x=0,0002. Gemessen wurde diese Kurve mit
der Babinet-Soleil Kompensation. Der Graph in der rechten oberen Ecke der
Abbildung zeigt die Debyekorrektur einer mit Kobalt dotierten Probe. Kurve
Nr. 1 ist die gemessene Doppelbrechungskurve, Nr. 2 ist der berechnete Anteil
durch die thermische Ausdehnung. Die Differenz liefert die Kurve in der großen
Abbildung.
31
Man erhält Kurven der in Abbildung 4.1.1 oben rechts gezeigten Form. Hierin
sind aber noch zwei Anteile vorhanden. Einmal existiert ein polarisations-optischer
Anteil, die Änderung der Doppelbrechung aufgrund von Änderungen der
Polarisation, und einen Anteil durch die thermische Ausdehnung des Kristalls, der
thermo-optische Anteil. Dieser ist für unsere Untersuchungen nicht von Interesse.
Deshalb werden die Messdaten durch das im folgenden beschriebene Verfahren
korrigiert. Danach liegt nur noch der thermo-optische Anteil der Doppelbrechung
vor. Beschrieben werden kann die thermische Ausdehnung εij durch folgende
Formel20,Fehler! Textmarke nicht definiert.:
ε ij = α ij ∆T
(4.1.1)
Hierbei ist αij der Ausdehnungskoeffizient und ∆T der durchlaufene
Temperaturunterschied.
Verknüpft ist die thermische Ausdehnung εij mit der Impermeabilität ∆Bij über
den elasto-optischen Effekt, wobei pijkl die elasto-optischen Koeffizienten sind.
∆Bij = pijkl ε kl
(4.1.2)
Die Impermeabilität ist verknüpft mit der Änderung des Brechungsindexunterschiedes.
 1
∆Bij = ∆
n
 ij




2
(4.1.3)
Die Tensorelemente αij werden in unserem Fall durch einen Mittelwert genähert,
welcher eigentlich den kubischen Fall beschreibt, in dem die Elemente und somit die
Ausdehnung für alle Richtungen gleich sind. Dieses Element wird im folgenden
einfach α genannt. Aus der Thermodynamik ist ein Ausdruck für den
Ausdehnungskoeffizienten bekannt:
α=
c
1  ∂V 

 = sijkl γ V
V
V  ∂T  P , N
(4.1.4)
V ist das Volumen des Kristalls, CV die spezifische Wärme und γ ist die
Grüneisenkonstante. Die Tensorelemente sijkl sind die elastischen Komplianzen.
Stellt man die oben genannten Formeln zusammen, so ergibt sich für die
Doppelbrechung das Folgende:
32
∆Bij = pijkl sijkl
cv
∆T ⇒ ∆n ∝ U (T )
V
(4.1.5)
Man sieht also, daß die Doppelbrechung zur inneren Energie U proportional ist.
Wir betrachten die innere Energie genauer. Nach dem Debeymodell gilt für sie:
T
U = 9nk b T 
θD
 xD
x3
 ∫ dx x
 0 e −1
(4.1.6)
Dabei ist θD=138K die Debyetemperatur, wobei gilt xD=θD/T. Den Wert für die
Debyetemperatur erhält man über die Messung der spezifischen Wärme cgemessen.
c gemessen =
Q
MT
(4.1.7)
Die Masse M des Kristalls kann durch M = N E m ersetzt werden, wobei NE die
Anzahl der Einheitszellen im Kristall und m die mittlere Masse in der Einheitszelle
ist. Die Debyeformel kann für kleine Temperaturen wie folgt genähert werden.
12 N Eνπ 4  T

C = c gemessen M =
5
θD
3

 k B

(4.1.8)
Dabei ist ν die Anzahl der Gitterschwingungen pro Einheitszelle und wird hier
wie im kubischen Fall auf eins gesetzt. kB ist die Boltzmannkonstante. Durch
Einsetzen erhält man nun:
c gemessen
12νπ 4 T 2
=
kB
5m θ D 3
(4.1.9)
Bei einer Auftragung der spezifischen Wärme c über T2 erhält man den
Vorfaktor der Gleichung und kann daraus θD errechnen.
Diese Debyefunktion kann nur numerisch gelöst werden. Durch eine Anpassung
dieser Werte an die Kurve im Hochtemperaturbereich 750K≤T≤850K, in dem nur
noch der thermische Anteil der Doppelbrechung von Bedeutung ist, und Abziehen
der beiden Kurven voneinander ergibt sich eine Kurve, die nur den polarisationsoptischen Anteil beinhaltet. Dies ist in Abbildung 4.1.1 zu sehen.
Eine genauere Betrachtung von Abbildung 4.1.1 zeigt einen Phasenübergang
zweiter
Ordnung
paraelektrischen
und
einen
Bereich.
langen
Im
Ausläufer
ferroelektrischen
der
Doppelbrechung
Bereich
läuft
im
die
33
Doppelbrechungsänderung bei Temperaturen kleiner als 100K in eine Sättigung. Die
Fluktuationen der Polarisation werden im Folgenden genauer untersucht. Die
Variation der Impermeabilität bzw. die Änderung des Doppelbrechungsunterschiedes
läßt sich mit Hilfe der Matrixnotation des Indikatrixformalismus wie folgt
beschreiben:
3
 1 
δ  2  = ∑ g ijF Pj2
 n  i j =1
(4.1.10)
Die gijF sind die freien elektrooptischen Koeffizienten und Pj ist die Polarisation in jRichtung. Für die lineare Doppelbrechung ergibt sich:
 n3 
∆nac = − 0  g11F − g12F P 2
 2 
(
)
(4.1.11)
Hierbei ist P=P3 in Richtung der polaren c-Achse. Der Wert n0 ist der
Hochtemperatur-Brechungsindex.
Die zeit- und raumgemittelte Autokorrelationsfunktion beschreibt die Schwankung
des Polarisationsmittelwertes, also des Ordnungsparameters.
2
P 2 = P + δP 2
(4.1.12)
Im paraelektrischen Bereich ist das Mittel der Polarisation Null und es bleiben nur
die
Fluktuationen
über.
Diese
lassen
sich
durch
das
Fluktuations-
Dissipationstherorem ausdrücken:
δP
2
k
k bT m r 3 r
= 3 ∫ χ (k )d k
8π 0
(4.1.13)
Die Polarisation wird hierbei durch ein Integral über die Suszeptibilität χ
ausgedrückt, wobei über die gesamte Brillouinzone integriert wird. Die Obergrenze
km ist die Wellenzahl am Rande der Brillouinzone. kb ist die Boltzmannkonstante.
Mit der Ornstein-Zernike Näherung, d.h. Enwicklung der Suszeptibilität χ für k→0
und der Annahme eines isotropen Systems folgt:
r
χ (k ) =
χ (0)
1+ ξ 2k 2
(
)
(4.1.14)
wobei χ(0)=ε0ε gilt. χ(0) ist die statische Suszeptibilität. Für sie gilt
χ (0) = ε 0 (ε − 1) ∝ t −γ . ξ (t ) = ξ 0± t −ν ist die Korrelationslänge im kritischen Bereich.
34
Sie ist ein Maß für die Reichweite der Korrelation. γ und ν sind die zugehörigen
kritischen Exponenten der Suszeptibilität und der Korrelationslänge. Ersetzt man die
kubische Brillouinzone nun durch eine Kugel mit 0≤k≤km=π/a, wobei a die
Gitterkonstante ist, so kann die Integration durchgeführt werden und es ergibt sich
eine Formel für die Doppelbrechung im Fluktuationsbereich21.
 n3k ε k
∆nacFlukt = − 0 B 20 m
 4π
(
)
1 − tan −1 k m t −ν 
 F
 g11 − g12F Tt 2ν −γ 

k m t −ν



(
)
(4.1.15)
t ist die reduzierte Temperatur.
Diese Funktion wird nun für den Temperaturbereich Tc≤T≤1,03Tc an die
Meßwerte angepaßt. Man erkennt, daß der Kurvenverlauf sehr gut für Werte nahe Tc
mit den gemessenen Werten übereinstimmt. Mit dem Verhältnis der kritischen
Amplituden im paraelektrischen bzw. ferroelektrischen von
1
2
für die
Korrelationslängen in der eckigen Klammer in Gleichung (4.1.15) läßt sich die
Kurve für Werte kleiner Tc fortsetzen. Im Vorfaktor kürzen sich die Amplituden von
Suszeptibilität und Korrelationslänge heraus. Der Wert
1
2
ist eigentlich das
Verhältnis der Amplituden der Korrelationslängen aus der Landau-Theorie. Für das
RFIM wurden aber bisher noch keine Werte gemessen, so daß auf die
Amplitudenverhältnisse aus der Landautheorie zurückgegriffen werden muß. Die
Extrapolationen sind in Abbildung 4.1.2 zu sehen (OZ).
35
6
fe
3
4
4
x
3
10
-1
10
-2
10
-3
1: SBN
2: Cr x=0,003
3: Cr x=0,006
4: Cr x=0,015
2
2
.
th
10 |∆nac - ∆nac |
5
|∆nac |
1
2
1
x
10
-3
-2
10
10
|T/Tc-1|
-1
10
0
OZ
OZ
0
0
100
200
300
400
500
600
700
800
Temperatur [K]
Abbildung 4.1.2: Debyekorrigierte Kurve der linearen Doppelbrechung für
Chrom dotierte Proben. Die schwarzen durchgezogenen Linien sind die
Ornstein-Zernike Kurven (OZ), welche die Fluktuationen beschreiben. Der
Ausschnitt zeigt den ferroelektrischen Anteil der Doppelbrechung nach Abzug
der OZ-Kurven.
Von den gemessenen Daten wurden die Ornstein-Zernike Kurven für T<Tc
abgezogen. Es bleibt nur der ferroelektrische Anteil ∆nacfe der Polarisationswerte
übrig. An diese Kurve wurde das folgende Potenzgesetz angepaßt.
P
2
 T
∝ 1 −
 Tc



2β
(4.1.16)
β ist der kritische Exponent des Ordnungsparameters. Alle Messungen wurden
für Chrom dotierte Proben mit x=0,003, x=0,006 und x=0,015 sowie für eine mit
Kobalt dotierte Probe mit x=0,0002 durchgeführt. Die gleichen Analysen im ferround paraelektrischen Bereich sind schon früher an mit Cer dotierten Proben von P.
Lehnen durchgeführt wordenFehler! Textmarke nicht definiert..
36
10
∆nac
ferro
0,15
10
10
-2
x
-3
ferro
0,10
-1
-3
10
∆nac
10
-2
10
-1
10
0
t
Cr:
x=0
x=0.003
x=0.006
0,05
x
0,00
0
100
200
300
Temperatur [K]
Abbildung 4.1.3: Ferroelektrischer Anteil der Chrom dotierten Proben mit
x=0,003, x=0,006 und x=0,015.
-1
∆nac
ferro
10
0,15
-2
10
ferro
0,10
-3
∆nac
10
-3
-2
10
10
10
-1
0
10
t
0,05
Co: x=0,0002
0,00
0
100
200
300
Temperatur [K]
Abbildung 4.1.4: Ferroelektrischer Anteil einer Kobalt dotierten SBN Probe mit
x=0,0002.
37
Aus den Anpassungen lassen sich zusätzlich noch die Übergangstemperaturen
für den Phasenübergang bestimmen. Eine erste Näherung für diesen Wert bekommt
man aus den Ableitungen der polarisationsoptischen Anteile der Kurven. Die
Ableitungen sind in Abbildung 4.1.5 dargestellt. Die Minima der Ableitungen,
welche mit den Phasenübergangstemperaturen zusammenfallen, verschieben sich mit
wachsender Dotierung immer weiter zu niedrigeren Temperaturen. Man erkennt für
wachsende Dotierungen immer breiter werdende Kurven, weil der Phasenübergang
mit der Größe der Dotierung immer weiter “ausgeschmiert” wird. Das macht für eine
Dotierung x=0,015 eine Anpassung der Ornstein-Zernike Formel an die Meßdaten
unmöglich.
-2
-4
4
th
-4
-1
d(|∆nac - ∆nac |)/dT [10 K ]
0
3
-6
-8
1:SBN
2:Cr x=0,003
3:Cr x=0,006
4:Cr x=0,015
5:Co x=0,0002
2
5
1
250
300
350
400
Temperatur [K]
Abbildung 4.1.5: Ableitungen der Doppelbrechungskurven der mit Chrom bzw.
Kobalt dotierten Proben. Man erkennt für wachsende Dotierungen eine
Verbreiterung der Kurven und eine Verschiebung der Minima zu niedrigeren
Temperaturen.
Insgesamt haben wir nun Werte für die kritschen Exponenten β, γ, und ν sowie
für die Curietemperatur Tc erhalten. In folgenden Tabellen sind alle Ergebnisse der
38
Cobalt und Chrom dotierten Proben sowie der schon früher gemessenen Cer
dotierten Proben zu sehen.
x
km
Tc
ν
γ
β
0
0.66 ±0.09
350.2 ±0.1
0.64 ±0.13
1.30 ±0.27
0.31 ±0.01
Cer 0,0066
0.56 ±0.01
328.0 ±0.1
0.69 ±0.01
1.36 ±0.02
0.35 ±0.01
Cer 0,0113
0.53 ±0.83
320.0 ±0.6
0.68 ±0.86
1.34 ±1.71
0.40 ±0.01
Cer 0,0207
0.63 ±0.34
290.9 ±1.3
0.79 ±0.27
1.58 ±0.51
0.46 ±0.01
Co 0,0002
0.54 ±0.07
348.0 ±0.5
0.64 ±0.13
1.28 ±0.29
0.30 ±0.01
Cr 0,003
0.57 ±0.10
342.2 ±0.3
0.65 ±0.11
1.29 ±0.22
0,33 ±0,01
Cr 0,006
0.58 ±0.14
321.3 ±0.1
0.66 ±0.15
1.30 ±0.29
0.40 ±0.01
Tabelle 4: Auswertung der Fluktuationen der Kobalt und Chrom dotierten
SBN-Proben und der ferroelektrischen Anteile der linearen Doppelbrechung
mit Ornstein-Zernike. Für die Cer dotierten Proben liegt in den Parametern
eine Tendenz zum RFIM vor. Chrom- bzw. Kobaltdotierung zeigt diese
Tendenz nicht.
Die km Werte in der ersten Spalte geben die Größe der Brillouinzone wieder. Da
km=π/a gilt, wobei a die Gitterkonstante ist, ergibt sich im Mittel ein Wert von
a=5,4Å ±0,5. In unserer Berechnung sind wir immer von einem isotropen System
ausgegangen. Dies ist aber nicht der Fall, denn SBN hat eine tetragonale Struktur. Es
liegen also zwei verschiedene Achsen vor, für die eine ist die Gitterkonstante
c=3,935Å, für die andere a=12,465Å.22,23 Unser ermittelter Wert liegt also
dazwischen. Man erkennt für die Cer dotierten Proben mit steigender Dotierung die
Tendenz vom 3D-Ising Modell zum 3D-Zufallsfeld Ising Modell. Bei der undotierten
Probe liegen nahezu die Werte des 3D Ising-Model vor. Hier gilt γ=1,24 und ν=0,63.
Mit steigender Dotierung wachsen die γ und ν Werte immer weiter an und nähern
sich den RFIM Werten von γ=1,89 ±0,17 und ν=1,02±0,06.24
Bei den Chrom bzw. Kobalt dotierten Proben hingegen ändern sich diese Werte
kaum. Wie in Kapitel 2.4 schon näher erläutert, liegt das an der Lage der
Dotierungen und ihrer Stärke. Cer setzt sich auf einen Strontiumplatz und erzeugt
über die Wechselwirkung mit dem nächsten Niobion, dem wesentlichen Träger der
Polarisation, das Zufallsfeldverhalten, da es eine positive Ladung mehr als das
Strontium trägt. Da Chrom sich auf einen Niobgitterplatz setzt und somit ein lokales
39
Dipolmoment aus dem Kristall eleminiert und die Entfernung zum nächsten
Polarisationsträger groß ist, baut sich bei einer Dotierung mit Chrom kein wirksames
Zufallsfeld auf.
Im Gegensatz zu den γ und ν Werten passen die β-Werte nicht in das Verhalten.
Sie laufen eher zum Molekularfeldwert von ½ anstatt zum RFIM Wert von
β=0,06±0,0716. Der Kurvenverlauf ist somit deutlich flacher und somit die
Änderung der Polarisation kleiner. Dies liegt daran, daß wir uns nicht im
Grundzustand des ferroelektrischen Bereichs befinden, welches ein eindomäniger
Zustand wäre. Tatsächlich zerfällt der Kristall in mehrere Domänen.25 Die
Doppelbrechung wird aber durch die Änderung der Wände zwischen diesen
Domänen beinflußt. Eine Domänenwand bedeutet entweder einen Bereich kleinerer
Polarisation oder ein Gebiet ohne Polarisation. In beiden Fällen ändert sich die
Doppelbrechung. Die β-Werte sind also über alle Domänen bzw. Domänenwände im
Meßbereich gemittelt.
Bei den bisherigen Untersuchungen der temperaturabhängigen Doppelbrechung
wurde das alte Messprogramm mit der Babinet-Soleil Kompensationsmethode
verwendet. Hierbei gibt es zwar die Möglichkeit, jeden Meßpunkt über die Steuerung
des Heiztisches auf 0,1K genau anzufahren, jedoch müßte dann solange gewartet
werden, bis sich die eingestellte Temperatur über den gesamten Kristall ausgebreitet
hat. Im Idealfall würde sich der Meßwert der Doppelbrechung nicht mehr ändern.
Erst dann könnte die nächste Temperatur angefahren und der nächste Meßpunkt
aufgenommen werden. Bei den bisherigen Kurven wurde immer eine möglichst
kleine Heizrate gewählt, die beim Heiztisch bei 0,1K/min liegt, und die
Doppelbrechungswerte alle fünf Sekunden aufgenommen.
Bei der Messung zur Abbildung 4.1.6 wurde die Steuerung des Heiztisches über
das neue Programm in so fern erweitert, daß jeder Meßpunkt angefahren und solange
gehalten werden kann, bis keine Änderung mehr vorliegt. Den genauen
Programmablauf kann man im Kapitel 3.5 nachlesen. Es wurde der Bereich des
Phasenübergangs einer x=0,0066 Cer dotierten Probe gemessen. Nach der alten
Meßmethode ergab sich ein Tc von 328K. Nun erhält man einen Wert von Tc≈332K.
Dies entspricht einer Abweichung von ≈1%. Man erwartet eigentlich ein kleineres Tc
bei einer vollständigen Relaxation der Temperatur. Dies ist hier nicht der Fall.
Möglicherweise deshalb, weil eine andere Probe mit vermeintlich gleicher Dotierung
40
benutzt wurde. Zu beachten ist hierbei noch, daß nur sehr wenige Punkte zur Bildung
der Ableitung vorlagen und das Minimum der Ableitung sehr nahe am Rand der
-1
d(|∆nac - ∆nac |)/dT [10 K ]
aufgenommenen Kurve liegt.
th
-4
-4
6,5
6,0
-5
-6
-7
-8
2
th
10 |∆nac - ∆nac |
7,0
320
330
340
Temperatur [K]
5,5
5,0
320
325
330
335
340
Temperatur [K]
Abbildung 4.1.6: Messung der linearen Doppelbrechung einer x=0,0066 Cer
dotierten Probe. Wie in den Messungen zuvor ist die Korrektur der Daten
(temperaturabhängiger Ausdehnungsanteil) durchgeführt und die Ableitung
gebildet worden. Jeder Meßpunkt wurde einzeln angefahren und für einen
Zeitraum von im Mittel fünf Minuten gehalten. Für die Übergangstemperatur
ergibt sich Tc=332K.
41
5 Hysteresemessungen
5.1 Dehnungs- und Polarisationsanteil der Doppelbrechung
In Kapitel 4 wurde festgestellt, daß bei der Ermittlung des kritischen Exponenten
β über alle Domänen bzw. Domänenwände gemittelt und die Werte somit verfälscht
wurden. Deshalb sollen an dieser Stelle die Eigenschaften dieser Domänen und ihr
Verhalten auf ein elektrisches Feld genauer untersucht werden. Eine 0,787 mm dicke
Cer dotierte Probe (Tc≈328K) wurde hierzu bei Temperaturen nahe Tc mit einem Feld
belegt, welches von 0 bis auf einen maximalen Wert von 200kV/m geregelt wurde.
Die Auftragung der gemessenen Kurven ist in Abbildung 5.1.1 zu sehen.
Man erkennt bei den Kurven, daß diese auch nach dem Überschreiten der
Koerzitivfeldstärke Ec, welche nach Messungen optischen Frequenzverdopplung
(SHG)26 und Hysteresemessungen nach Granzow27,28 um 120kV/m liegt, noch weiter
ansteigen. Eigentlich würde man hier eine Sättigung erwarten, da zu diesem
Zeitpunkt ein eindomäniger Zustand vorliegen sollte. Das weitere Ansteigen muß
also auf einem anderen Effekt beruhen.
Schaut man sich die Zusammenhänge zwischen der Doppelbrechung und einem
elektrischen Feld genauer an sieht man, daß nicht nur ein Anteil aufgrund der
Polarisationsänderung existiert, sondern auch einer aufgrund der Dehnung bzw.
Stauchung des Kristalls29,30, also der piezoelektrische Effekt. Die Abhängigkeit der
Doppelbrechung
von
den
Dehnungsänderungen
Matrizenformalismus genauer beschrieben werden.
42
soll
hier
mit
Hilfe
des
3
300K
318K
328K
338K
2
1
0
3
10 ∆n
3
2
1
0
-200
-100
0
100
200
373K
3
2
1
0
-200
-100
0
100
200
Feld [kV/m]
Abbildung 5.1.1: Hysteresekurven einer mit Cer dotierten SBN Probe mit
x=0,0066 bei Temperaturen von 300K bis 373K. Die eingetragenen Pfeile zeigen
die Lage von Ec. Die Übergangstemperatur liegt bei dieser Höhe der Dotierung
bei Tc≈328K.
Ein elektrisches Feld erzeugt in der Probe eine piezoelektrische Dehnung ε,
wobei hier mit dijk den piezoelektrischen Koeffizienten allgemein gilt:
43
ε jk = d ijk ⋅ Ei
 ε1   ⋅
  
ε 2   ⋅
ε   ⋅
 3=
ε 4   ⋅
  
 ε 5   d 24
ε   ⋅
 6 
(5.1.1)
⋅
⋅
⋅
d 24
⋅
⋅
d 31  E1 
 
d 31  E2 
d 33  E3 
 
⋅  ⋅ 
 
⋅  ⋅ 
⋅  ⋅ 
(5.1.2)
Insgesamt bleiben also in unserem Falle mit dem elektrischen Feld E in c-Richtung
nur drei Komponenten übrig:
ε 1 = d 31 E3
ε 2 = d 31 E3
(5.1.3)
ε 3 = d 33 E3
Das sind die Dehnungen innerhalb der Ebene (ε1 und ε3) bzw. senkrecht dazu (ε2).
Desweiteren ist die Dehnung über den elasto-optischen Effekt mit der
Impermeabilität ∆Bij und somit auch mit der Doppelbrechung verknüpft.
∆Brs = prsjk ε jk
∆ni = −
(5.1.4)
1
(n0 )3 ∆Bi
2
(5.1.5)
Hierbei ist n0 der Hochtemperaturbrechungsindex und hat den Wert 2,34.
Im Falle eines tetragonalen Systems der Klassen 4mm bzw. 4/mmm, wie es bei
uns vorliegt, ergibt sich eine Darstellung der Form:
 ∆B1   p11

 
 ∆B2   p12
 ∆B   p
 3  =  31
 ∆B4   .
 ∆B   .
 5 
 ∆B   .
 6 
p12
p11
p31
.
.
.
p13
p13
p33
.
.
.
.
.
.
p 44
.
.
.
.
.
.
p 44
.
.  ε 1 
 
.  ε 2 
.  ε 3 
 
.  ε 4 
.  ε 5 
p66  ε 6 
(5.1.6)
Daraus ergibt sich:
∆B1 = p11ε 1 + p12 ε 2 + p13ε 3
44
(5.1.7)
∆B3 = p31ε 1 + p31ε 2 + p33ε 3
(5.1.8)
Andere Komponenten sind für uns nicht relevant.
Für die Änderung der Differenz ∆n1 - ∆n3, gilt somit:
1
δ (∆n13 ) = − n03 (∆B1 − ∆B3 )
2
1
= − n03 [( p11 − p31 )ε 1 + ( p12 − p31 )ε 2 + ( p13 − p33 )ε 3 ]
2
1
= − n03 [( p11 − p31 )d 31 + ( p12 − p31 )d 31 + ( p13 − p33 )d 33 ]⋅ E3
2
1
= − n03 [( p11 + p12 − 2 p31 )d 31 + ( p13 − p33 )d 33 ]⋅ E3
2
(5.1.9)
Zu beachten ist hier noch, daß die Komponente 1 mit der a-Achse und die
Komponente 3 mit der c-Achse des Kristalls übereinstimmt.
Mit Kenntnis der prsjk bzw. dijk Werte ist es nun möglich, den Dehnungsanteil der
feldabhängigen Doppelbrechungsdaten zu berechnen. Hierbei ist ( d 31 = 70 pm
V ,
31
32
d 33 = 200 pm
V ) , (p11=0,06, p12=0,08, p13=0,17, p31=0,09 und p33=0,23) . Die prsjk-
Werte sind eigentlich an einer Sr0.5Ba0.5Nb206 Probe gemessen, jedoch sind es die
einzig vorliegenden und müssen deshalb für eine Abschätzung reichen.
Für den Anteil mit dem Faktor d31, der für die Nichtdiagonalkomponente der
Dehnung steht, ergibt sich für ein elektrisches Feld von 200 kV/m ein Wert von
δ (∆nac ) = 0,3 ⋅10 −5 , für den d33 Wert der Diagonalkomponente erhält man
δ (∆nac ) = 1,3 ⋅10 −5 . Die Änderung der Kurve über einen 200kV/m Bereich ist mit
einen Wert im Bereich von δ(∆nac)=10-3 bei niedrigen Feldern jedoch deutlich
größer. Die Dehnung macht also dort nur ein 1% des Effektes aus. Jedoch laufen die
Kurven für hohe Felder in einen Bereich, in dem die Dehnung die größte Rolle spielt.
Die Änderung der Dicke der Probe spielt hier keine Rolle. Nach Gleichung
(5.1.3) gilt ε3=d33E3. Dies ergibt für ein Feld von E3=200kV/m eine relative
Dickenänderung von ε3=4⋅10-4. Eine ohne angelegtes Feld 1mm dicken Probe ändert
ihre Dicke also zu dem Wert d=1,0004mm. Setzt man diesen Wert in die Gleichung
(3.1.8) ein, so ergibt sich bei einem gefahrenen Schritt für die unkorrigierte Dicke ein
Wert von δ(∆nac)=1,901⋅10-8 und für die korrigierte Dicke ein Wert von
δ(∆nac)=1,9005⋅10-8, also ein Unterschied von 5⋅10-12 pro gefahrenem Schritt.
45
Um den erwarteten linearen Bereich für hohe Felder auswerten zu können,
wurde eine weitere Messung bei T=318K gemacht und bis zu einer Feldstärke von
E≈600kV/m hochgemessen. Diese Messung ist in Abbildung 5.1.2 darstellt.
T=318K
4
3
10 ∆nac
3
2
1
-600
-400
-200
0
200
400
600
E [kV/m]
Abbildung 5.1.2: Hysteresemessung bei T=318K. Es wurde solange gemessen,
bis
bei
hohen
Feldern
nur
noch
eine
lineare
Änderung
der
Doppelbrechungswerte zu erkennen war. In diesen Bereichen wurden dann
Geraden angepaßt.
In diesen hohen Bereichen konnte eine Gerade angepaßt werden, deren Steigung mit
dem errechneten Wert für die Dehnung übereinstimmen sollte. Im Mittel ergab sich
aus beiden Anpassungen ein Wert von δ (∆nac ) = 3,8 ⋅10 −6
m
⋅ E mit E der
kV
elektrischen Feldstärke. Zum Vergleich betrachten wir hier wieder eine
Feldänderung von 200kV/m. Dafür ergibt sich ein Wert von δ (∆nac ) = 7,6 ⋅10 −4 .
Dieser Wert liegt in der gleichen Größenordnung wie der oben Berechnete.
Gleichwohl scheint die berechnete Änderung der Doppelbrechung immer noch
niedriger als die Berechnete. Dieser Fehlbetrag verringert sich offenbar beim
46
Abkühlen. Dazu vergleiche man die asymptotischen Steigungen
d (∆n )
in Abbildung
dE
5.1.1, die deutlich bei tiefen Temperaturen abflachen. Vermutlich hat dies seine
Ursache in der intrinsischen Unordnung des Relaxorsystems, dessen Eindomänigkeit
erst bei tieferen Temperaturen in hohen Feldern erreicht werden kann.
Abschließend werden die berechneten Geraden von der gemessenen Kurve
abgezogen, um nur noch den Polarisationsanteil der Doppelbrechung vorliegen zu
haben. Aufgetragen wurde dies in Abbildung 5.1.3. Wie schon aus anderen
Messungen der Polarisation bekannt,33 verläuft auch hier die Kurve im Bereich der
Koerzitivfeldstärke sehr steil. Jedoch weist die Kurve im Gegensatz zu Messungen
der Polarisation P nach T. Granzow starke Verrundungen auf, welche auf ein starkes
Pinning der Domänen schließen läßt. Zum Vergleich der beiden Kurven wurde die
Polarisation quadriert und in Abbildung 5.1.4 dargestellt. Der Wert für die
Koerzitivfeldstärke Ec liegt bei der Doppelbrechungshysterese bei ≈70kV/m.
2,0
3
10 ∆nac
1,5
1,0
0,5
0,0
-600
-400
-200
0
200
400
600
E [kV/m]
Abbildung 5.1.3:
Polarisationsanteil
der
linearen
Doppelbrechung
aus
Abbildung 5.1.2 nach Abzug des Dehnungsanteils.
47
0,08
0,04
2
2
4
P [C /m ]
0,06
0,02
0,00
-600
-400
-200
0
200
400
600
E [kV/m]
Abbildung 5.1.4: Polarisationshysterese einer SBN-Probe mit einer Cer
Dotierung mit x=0,0066.
48
6 Feldinduzierte Zeitabhängigkeiten der linearen
Doppelbrechung
6.1 Kurvenbeschreibung und Darstellung der Messungen
In diesem Kapitel sollen die Meßkurven und der Meßvorgang beschrieben
werden. Bei allen Messungen wurde eine mit Cer dotierte SBN Probe mit x=0,0066
verwendet, bei der die Übergangstemperatur, wie in Tabelle 4 zu sehen, bei Tc=328K
liegt. Um einheitliche Meßbedingungen zu gewährleisten, wurde vor jeder Messung
die Probe auf eine Temperatur über 750K gebracht und damit das Gedächtnis der
Probe gelöscht. Nach ungefähr einer Stunde Wartezeit wurde langsam bis zur
Meßtemperatur abgekühlt. Es wurde bei Temperaturen von 318K, 328K und 328K
jeweils mit einer Feldstärke von 64kV/m, 128kV/m, 192kV/m und 256kV/m
gemessen. Nach dem Start des Meßprogramms wurden zuerst einige Punkte
abgewartet, um zu sehen, ob noch Änderungen im Signal vorliegen. Erst dann wurde
ein Feld hinzugeschaltet. Nun wurde die Aufpolarisation so lange aufgenommen, bis
die Sättigung nahezu erreicht war. Sobald dies der Fall war, wurde das Feld wieder
abgeschaltet und wieder solange gewartet, bis nahezu die Sättigung erreicht wurde.
Der sich ergebende Meßablauf kann in Abbildung 6.1.1 betrachtet werden.
49
10
Es liegen kaum noch
Signaländerungen vor
8
6
∆nac*10
4
Abschalten des Feldes
4
Messkurve am Beispiel
64kV/m, 338K
2
0
-2
Einschalten des Feldes
0
2000
4000
6000
8000
Zeit[s]
Abbildung
6.1.1:
Beispiel
einer
feldinduzierten
Meßkurve
und
des
Meßvorgangs.
Die Abbildung 6.1.2, Abbildung 6.1.3 und Abbildung 6.1.4 zeigen nun alle
gemessenen Kurven aufgrund der Vergleichbarkeit in einer Auftragung, bei der die
∆n-Achse auf die gleichen Bereiche festgelegt wurden. Bei der Abbildung 6.1.2 und
Abbildung 6.1.3 ist dies auch für die Zeitachse der Fall. Für Abbildung 6.1.4 wurde
eine andere Achse gewählt, da eine Messung über einen deutlich längeren Zeitraum
durchgeführt wurde. Dies wurde gemacht, um sicher zu gehen, daß auch bei einem
größeren Zeitintervall keine Änderungen mehr vorliegen.
50
4
318K
256kV/m
∆nac*10
3
3
192kV/m
2
128kV/m
1
64kV/m
0
0
5000
10000
15000
Abbildung 6.1.2: Feldinduzierte Messung bei T=318K≈
≈ Tc-10K. Die Messungen
lieferten relative Daten, d.h. ein absoluter Nullpunkt liegt nicht vor. Die Lage
der Kurven relativ zur Ordinate ist also willkürlich.
4
256kV/m
3
∆nac*10
3
192kV/m
2
128kV/m
1
328K
64kV/m
0
0
5000
10000
15000
Zeit [s]
Abbildung 6.1.3: Feldinduzierte Messung bei T=328K≈
≈ Tc. Genau wie in
Abbildung 6.1.2 ist die Lage der Kurven relativ zur Ordinate willkürlich.
51
4
256kV/m
∆nac*10
3
3
192kV/m
2
128kV/m
1
64kV/m
338K
0
0
5000
10000
15000
20000
25000
Zeit [s]
Abbildung 6.1.4: Feldinduzierte Messung bei T=338K≈
≈ Tc. Dies liegt im
paraelektrischen Bereich der Probe. Zur Lage der Kurven siehe Beschriftung
von Abbildung 6.1.2.
Zu beachten ist in allen Auftragungen, daß die Werte von Hand an die
entsprechenden Stellen der ∆n-Achse verschoben wurden, damit alle Kurven in einer
Graphik übereinander liegen und sich nicht überschneiden. Daß die Kurven mit
höherem Feld also höher liegen ist kein Meßergebnis, sondern willkürlich gewählt.
Schaut man sich die Kurven jetzt genauer an, so erkennt man als erstes, daß die
Sprünge beim Abschalten des Feldes mit steigender Temperatur immer runder
werden. Bei T=318K ist eigentlich keine Krümmung zu erkennen. Bei T=328K ist
eine leichte Rundung zu sehen und bei T=338K ist diese stark ausgeprägt. Zu
beachten ist bei T=338K noch die unterschiedliche Auftragung auf der Zeitachse. Die
Rundung wäre bei gleicher Auftragung noch stärker. Desweiteren nimmt die Größe
der Änderung ebenfalls mit steigender Temperatur zu. Die Größe dieser Änderungen
ist in Tabelle 5 nachzulesen. Bei einigen Messungen konnte der Schrittmotor
möglicherweise den großen Änderungen in der Doppelbrechung nicht mehr folgen.
In diesem Fall könnte eine Phasenänderung von 2π ausgelassen worden sein. Bei
genauerem Hinsehen ist bei der Kurve T=318K, E=256kV/m zu sehen, daß hier der
52
Schrittmotor sogar beim Abschalten des Feldes erst einmal in die verkehrte Richtung
loslief.
Feldstärke/[kV/m]
318K
328K
338K
64
-
1,756⋅10-4
5,16⋅10-4
128
2,30⋅10-4
3,64⋅10-4
4,82⋅10-4
192
0,34⋅10-4
2,77⋅10-4
4,09⋅10-4
256
2,02⋅10-4
0,87⋅10-4
5,54⋅10-4
Tabelle 5: Polarisationsänderung nach Abschalten des Feldes. Es wurde die
Differenz zwischen dem letzten Wert mit Feld und dem letzten Meßwert
gebildet.
Bei der Aufpolarisation ist hingegen kein so deutlicher Unterschied in den
Meßkurven zu erkennen. Bei allen Temperaturen sind zwar Rundungen zu sehen
welche auch mit steigender Temperatur zunehmen, jedoch sind bei T=318K keine
Sprünge festzustellen. In Tabelle 6 sind die Polarisationsänderungen nach dem
Einschalten des Feldes aufgeführt.
Feldstärke/[kV/m]
318K
328K
338K
64
1,22⋅10-4
2,67⋅10-4
1,50⋅10-4
128
1,41⋅10-4
3,72⋅10-4
5,28⋅10-4
192
3,37⋅10-4
5,11⋅10-4
6,41⋅10-4
256
5,17⋅10-4
3,41⋅10-4
18,24⋅10-4
Tabelle 6: Polarisationsänderung nach Einschalten des Feldes. Die Differenz
wurde aus dem ersten Wert der Messung und dem letzten Wert der
Aufpolarisation ermittelt.
Man erkennt, daß die Werte mit steigender Temperatur und steigendem Feld größer
werden, was in Abbildung 6.1.5 aufgetragen wurde. Dies ist auch zu erwarten, da die
Domänen- bzw. Clusteränderungen und Polarisationsänderungen größer werden.
53
20
338K
Polarisationsänderung nach
Einschalten des Feldes
∆n*10
4
15
10
5
318K
328K
0
50
100
150
200
250
Feld [kV/m]
Abbildung 6.1.5: Polarisationsänderung nach dem Einschalten des Feldes. Der
Ausreißer für T=328K, E=64kV/m ist mit einem Nachregeln des Schrittmotors
in die verkehrte Richtung zu erklären. Siehe hierzu Abbildung 6.1.3.
6.2 Relaxation nach Feldeinschalten
Um Aussagen über das Domänenverhalten von SBN machen zu können, wurden
im ersten Durchgang die Aufpolarisationen der Kurven untersucht. Angesetzt wurde
mit einem gestreckten Exponentialgesetz nach Kohlrausch-Williams-Watts (KWW),
wobei Pind≈∆n1/2 gelten soll.14

  t  β 
∆n = A * 1 − exp −   
  τ  



1
2
(6.2.1)
Diese Untersuchungen lieferten nur für die Temperaturen 318K und 338K
sinnvolle Werte. Für 328K wachsen die Werte für τ immer weiter an. Im Bereich der
Übergangstemperatur sind die Fluktuationen zu groß. Für alle Temperaturen zeigt
sich ein Anwachsen der β-Werte mit wachsendem Feld. Der β-Wert hängt mit der
Größenverteilung der Domänen zusammen und nähert sich mit wachsendem Feld
immer mehr dem Wert β=1. Dies würde einem Zustand mit uniformen Domänen mit
54
nur einer Relaxationszeit τ entsprechen. τ wächst, zumindest bei T=318K, mit der
Größe des angelegten Feldes. Anzunehmen ist, daß die Dömanengrößenverteilung
sich immer weiter zu größeren Domänen verschiebt, die im Einzelnen eine größere
Relaxationszeit als die Kleinen besitzen. Alle Werte der Anpassungen für Gleichung
(6.2.1) sind in Tabelle 7 zu sehen.
Temperatur/Feldstärke
P∞
τ
β
318K, 64 kV/m
0,022 ±0,0001
20,72 ±0,61
0,22 ±0,004
318K, 128kV/m
0,020 ±0,0005
141,05 ±29,70
0,19 ±0,006
318K, 192 kV/m
Nicht auswertbar
318K, 256 kV/m
0,040 ±0,007
421835 ±399191 0,26 ±0,01
328K, 64 kV/m
0,042 ±0,001
186173 ±37699
0,24 ±0,002
328K, 128 kV/m
0,018 ±0,001
132,03 ±1,08
0,26 ±0,002
328K, 192 kV/m
0,017 ±0,001
447986 ±188405 0,18 ±0,002
328K, 256 kV/m
0.005 ±0.001
1635.6 ±42.1
0.56 ±0,007
338K, 64 kV/m
0,014 ±0,0001
407,2 ±35,6
0,18 ±0,002
338K, 128 kV/m
0,004 ±4⋅10-6
13,1 ±0,3
0,27 ±0,003
338K, 192 kV/m
0,0033 ±2⋅10-6
478,9 ±1,8
0,30 ±0,001
338K, 256 kV/m
Nicht auswertbar
Tabelle 7: Aufpolarisationsauswertung nach KWW. Für die Kurve bei T=318K
mit einer Feldstärke E=192 kV/m und die Kurve bei T=338K und E=256 kV/m
liegen keine Anpassungen vor.
Eine Auftragung der Meßkurven sind in Abbildung 6.2.1 und Abbildung 6.2.2 zu
sehen. Man erkennt, daß die Anpassungen nur am Anfang mancher Kurven versagen.
Dies kann mit den vorher erwähnten Schwierigkeiten des Schrittmotors
zusammenhängen, große Änderungen in der Doppelbrechung richtig aufzunehmen.
Die in Kapitel 5.1 beschriebene Dehnung des Kristalls ist ein anderer Grund für die
Abweichungen der Kurven von den Anpassungen mit einer KWW-Funktion. Dort
wurde bei einer Feldstärke von 200 kV/m eine Änderung von ∆nac≈10-4 festgestellt.
Die Änderungen beim Anschalten des Feldes sind von der gleichen Größenordnung.
So ergibt sich bei der Kurve bei T=338K und 50kV/m ein Wert von ∆nac≈8,5⋅10-5
zwischen dem letzten Wert vor Anlegen des Feldes und dem ersten Wert nach
Anlegen des Feldes.
55
Der Einfluß der Dehnung ist jedoch nur in den ersten Meßwerten zu sehen.
Danach ändert sich die angelegte Spannung nicht mehr, und es treten nur noch
Relaxationsänderungen auf. Das Gleiche gilt für den Bereich des Feldabschaltens.
Die ersten Punkte enthalten Dehnungsanteile und Relaxationen der Domänen, der
Rest nur Relaxationseigenschaften.
0,02
∆nac
1/2
64 kV/m
128 kV/m
0,01
192 kV/m
0,008
318K
0,006
256 kV/m
Aufpolarisation
0,004
Abbildung
100
6.2.1:
Zeit [s]
1000
Aufpolarisationsanpassung
für
T=318K.
Nahe
der
Übergangstemperatur wachsen die Fluktuationen des Ordnungsparameters
immer weiter an.
56
∆n
1/2
0,02
0,01
64 kV/m
256 kV/m
0,008
0,006
338K
128 kV/m
0,004
0,002
Aufpolarisation
192 kV/m
100
Zeit [s]
1000
10000
Abbildung 6.2.2: Aufpolarisation für T=338K.
6.3 Relaxation nach Feldabschalten
Die Betrachtung der Relaxationskurven nach Feldabschalten muß sich auf die
Kurven bei T=338K beschränken. Nur hier liegen Kurven mit genügend deutlicher
Relaxation vor. Bei allen anderen ist der Einfluß der Fluktuationen zu groß. Deshalb
ist bei T=318K bzw. T=328K ist fast nur ein Sprung aufgrund der Dehnung des
Kristalls zu erkennen.
Es wurden Anpassungen mit KWW sowie mit einem Potenzgesetz versucht,
  t β 
∆n = a exp −   
  τ  
(6.3.1)
∆n = at β .
(6.3.2)
Hierbei lieferten die Potenzgesetzanpassungen die besseren Ergebnisse. Diese sind in
Tabelle 8 aufgeführt. In dieser Auswertung steigen die β-Werte genau wie in der
Aufpolarisationsauswertung mit steigendem Feld. Die dazugehörigen Kurven sind in
Abbildung 6.3.1 dargestellt. Die einzige Ausnahme ist hier der Wert für E=256kV/m,
welcher mit β=0,06 deutlich zu klein ist. Dies erklärt sich mit der schlechten
57
Anpassung an die gemessenen Daten. Bei kleinen Zeiten liegt die angepaßte Kurve
überhaupt nicht auf der gemessenen Kurve. Weiterhin sind die Daten nicht ideal. In
einem großen Bereich der Anpassung liegt keine glatte Kurve vor, sondern es treten
mehrere Sprünge auf, die das Ergebnis verfälschen.
E[kV/m]
a
β
64
0,0012
0,19
128
0,0011
0,25
192
0,0016
0,38
256
0,0010
0,06
Tabelle 8: Potenzgesetzanpassung der Relaxationdaten für T=338K. Der
kritische Exponent β steigt mit wachsen der Feldstärke E an.
0,002
∆n
64kV/m
128kV/m
1E-3
8E-4
192kV/m
6E-4
338K
Potenzgesetzanpassung
der Relaxationsdaten
4E-4
256kV/m
2E-4
100
Zeit [s]
1000
10000
Abbildung 6.3.1: Relaxationsauswertung für T=338K mit einem Potenzgesetz.
Bei den Anpassungen der Kurven gab es deutliche Probleme mit der
Potenzgesetzanpassung. Eine Anpassung mit KWW lieferte überhaupt keine
vernünftigen Ergebnisse. Es war schwierig, eine vernünftige Kurve anzupassen. Hier
fallen zwei mögliche Ursachen direkt ins Auge. Die erste sind die großen
Änderungen in den Doppelbrechungswerten, die SBN nun einmal mit sich bringt.
Dies könnte vielleicht durch kleinere Felder verhindert werden.
58
Die zweite Ursache liegt in den großen Fluktuationen des Ordnungsparameters
bzw. der Doppelbrechung bei Temperaturen nahe Tc. Um den letzten Punkt genauer
zu untersuchen, wurden weitere Messung bei T=308K und T=348K gemacht, also
20K von der kritischen Temperatur entfernt. Hier wurden nur noch Felder der Größe
64kV/m und 256kV/m angelegt. Leider ist eine Datenreihe durch fehlenden
Speicherbereich zerstört worden, so daß nur drei Meßkurven vorliegen, welche in
Abbildung 6.3.3 dargestellt sind.
256kV/m
3
308K
64kV/m
∆n*10
3
2
348K
1
256kV/m
0
0
5000
10000
15000
Zeit [s]
Abbildung 6.3.2: Feldinduzierte Doppelbrechung bei Tc± 20K.
Bei den beiden Kurven für T=308K ist wieder der Sprung beim Übergang zum
feldabgeschalteten Zustand zu erkennen, doch auch für die Temperatur T=348K ist
keine eindeutige Relaxation zu sehen, vielmehr scheint hier auch nur ein Sprung
vorzuliegen, was eine Auswertung unmöglich macht. Deshalb ist für alle nur eine
Aufpolarisationsauswertung gemacht worden, die in Abbildung 6.3.3 zu sehen ist.
Die Entfernung von 20K vom Phasenübergang hatte keinen Einfluß auf die Güte der
Anpassungen. Wenn man sich diese in der Abbildung genauer ansieht, scheinen sie
höchstens schlechter geworden zu sein. Die Anpassungen für die Temperaturen
T=308K verlaufen bei am Anfang der Kurve nicht auf den gemessenen Daten. Das
spiegelt sich auch in den Ergebnissen der KWW Anpassungen in Tabelle 9 wider.
59
Das β läuft für große Felder nicht gegen den Wert 1, was zu einem eindomänigen
Zustand passen würde, der damit eigentlich angestrebt werden müßte, sondern wird
sowohl für T=308K als auch für T=348K noch kleiner als alle Werte, die bei den
bisherigen Auswertungen vorlagen. Dies würde nur Sinn machen, wenn zu Beginn
eine Domänenverteilung gleichartiger Domänen vorliegt, d.h. alle Domänen hätten
annähernd dieselbe Größe. Das angelegte Feld würde dann das Verhältnis
verschieben. Dies erklärt aber keinen kleineren Wert als bei Temperaturen nahe Tc,
da dort ähnliche Bedingungen vorliegen müßten und ein angelegtes Feld denselben
Einfluß zeigen sollte. Bei T<Tc wirkt wahrscheinlich der ferroelektrische Zustand der
Umpolung entgegen. Bei T>Tc verursacht die thermische Aktivierung eine breite
Domänengrößenverteilung.
Der größere Abstand scheint keinen Vorteil gebracht zu haben. Man ist mit nur
20K Abstand von Tc noch zu nahe und die Fluktuationen sind noch zu groß.
0,04
64kV/m, 308K
1/2
0,03
∆nac
256kV/m, 348K
0,02
256kV/m, 308K
50
100
500
1000
5000
10000
Zeit [s]
Abbildung 6.3.3: Aufpolarisationsauwertungen für die Temperaturen T=308K
und T=348K.
60
P∞
τ
β
308K, 64 kV/m
0.037 ±4⋅10-6
33.1 ±0.2
0.36 ±0.001
308K, 256kV/m
0.018 ±0.001
3.38 ±0.13
0.15 ±0.003
348K, 256 kV/m
0.029 ±0.001
145.1 ±25.5
0.11 ±0.002
Tabelle 9: Aufpolarisationsdaten bei T=308K und T=348K. Auch bei Messungen
20K über bzw. unter Tc beeinflussen starke Fluktuationen die Meßergebnisse.
61
7 Zusammenfassung
In dieser Arbeit wurde das Ferroelektrikum Sr0.61Ba0.39Nb2O6 (SBN) mit
verschiedenen Dotierungen von Chrom mit x=0,003, x=0,006 und x=0,015 sowie
einer Dotierung mit Kobalt mit x=0,0002 untersucht.
Die Temperaturabhängigkeit der linearen Doppelbrechung über einen Bereich
von 80-850K wurde aufgenommen und mit einer Ornstein-Zernike Anpassung erhielt
man Werte für die Übergangstemperatur Tc und die kritischen Exponenten ν, γ und β.
Dabei ergab die Analyse, daß sowohl Chrom- als auch Kobalt-dotierte Proben das
Zufallsfeldverhalten von SBN im Gegensatz zu schon früher gemessenen Cerdotierten Proben nicht beeinflussen.
Hysteresemessungen an SBN zeigen einen Beitrag des piezoelektrischen Effekts,
welcher für kleinere Felder vernachlässigbar, für größere Felder aber die Sättigung
der Doppelbrechungskurven verhindert. Diese zeigen bei großen Feldstärken ein
lineares Verhalten, was zu einem großen Anteil auf diesen Effekt zurückzuführen ist.
Eine Anpassung einer linearen Funktion in diesem Bereich und Subtraktion des
Ergebnisses von der gemessenen Kurve liefert den Anteil der Polarisation an der
gemessenen Doppelbrechung.
Weitere
Messungen
der
feldinduzierten
Zeitabhängigkeit
der
linearen
Doppelbrechung wurden für eine genauere Analyse der Domänenstruktur von SBN
durchgeführt. Hierbei wurde mit Feldern über und unter der Koerzitivfeldstärke Ec
gearbeitet und Temperaturen bis 20K über bzw. unterhalb von Tc gewählt. Sowohl
Potenzgesetzanpassungen
als
auch
Anpassungen
mit
einem
gestreckten
Exponentialgesetz nach Kohlrausch-Williams-Watts wurden durchgeführt und
weißen eine breite Domänengrößenverteilung nach.
Ein weiterer Beitrag zu dieser Arbeit war dem Aufbau einer Meßapparatur zur
kontinuierlichen Messung der linearen Doppelbrechung gewidmet. Hierzu diente
eine Modifikation des vorhandenen Aufbaus nach Babinet-Soleil zum Aufbau nach
Sénarmont, in dem zur Aufnahme des Meßsignals ein rotierender Analysator dient.
Dies erhöht einerseits die Meßgenauigkeit um den Faktor 10, andererseits bietet
diese
Meßmethode
die
Möglichkeit,
größere
Bereiche
mit
hoher
Doppelbrechungsänderung ohne Unterbrechung zu messen.
Desweiteren war die Programmierung eines neuen Meßprogramms mit Visual
C++ vorgesehen, welches neben einer graphischen Oberfläche und der damit
62
verbundenen einfachen Bedienung die Möglichkeit bietet, sowohl Messungen der
temperaturabhängigen Doppelbrechung, feldabhängige Zeitabhängigkeiten der
Doppelbrechung
als
auch
Hystereseeigenschaften
der
Doppelbrechung
durchzuführen.
63
Danksagung
Herrn Prof. Dr. Kleemann möchte ich für die Möglichkeit danken, neben einem
interessanten Themenbereich der Physik auch auf dem Gebiet der Programmierung
tätig sein zu können.
Meinen Betreuer Dipl. Phys. P. Lehnen danke ich für die zahlreichen Diskussionen
und Hilfestellungen beim Schreiben der Diplomarbeit und bei der Erstellung der
Poster.
Dr. R. Pankrath von der Uni Osnabrück danke ich für die zur Verfügung gestellten
Proben.
Dr. Th. Woike und seine Arbeitsgruppe an der Uni Köln danke ich für die
Bearbeitung der Proben.
Dipl. Ing. M. Aderholz danke ich für die Unterstützung bei der Umsetzung des neuen
Aufbaus der linearen Doppelbrechung und für die Beantwortung immer
wiederkehrender Fragen, die speziell die Meßsignalanpassung betreffen.
Meinen Freund A. Hochstrat danke ich für die langjährige Zusammenarbeit über eine
zweistellige Semesterzahl hinaus.
Dr. Christian Binek danke ich für möglichst einfache Erklärungen der
verschiedensten Sachverhalte.
Vor allen anderen danke ich meinen Eltern, die auch über meine lange Studienzeit
hinaus immer zu mir gehalten haben.
64
A. Eidesstattliche Erklärung
Hiermit erkläre ich, daß ich die vorliegende Diplomarbeit selbständig und nur unter
Verwendung der angegebenen Quellen angefertigt habe.
Duisburg, den 23. April 2001
65
Literatur
1
A. M. Glass, „Investigation of the electrical properties of Sr1-xBaxNb2O6 with
special reference to pyroelectric detection“, J. Appl. Phys. 40, 4699 (1969)
2
K. Tada, T. Murai, M. Aoki, K. Muto, K. Awazu, „Electrooptic light beam
deflection with Sr0.75Ba0.25Nb2O6 prism“, Jpn. J. Appl. Phys. 11, 1622 (1972)
3
E. L. Venturini, E. G. Spencer, A. A. Ballman, J. „Elasto-optic properties of
Bi12GeO20, Bi12SiO20, and SrxBa1-xNb2O6“, J. Appl. Phys. 40, 1622 (1969)
4
D. M. Pepper, J. Feinberg und N. W. Kuchtarew, „Der photorefraktive Effekt“,
Spektrum der Wissenschaft, 72 (1990)
5
S. C. Abrahams, P. B. Jamieson, J. L. Bernstein, „Ferroelectric tungsten bronze-
type crystal structures. Iii. Potassium lithium niobate K(6-x-y)Li(4+x)Nb(10+y)O30“, J.
Chem. Phys. 54, 2355 (1971)
6
Y. Imry und S. Ma, „Random Field Instability of the Ordered State of Continuous
Symmetry“, Phys.Rev.Lett. 35, 1399 (1975)
7
V. Westphal, W. Kleemann, M. D. Glinchuk, „Diffuse Phase Transitions and
Random-Field-Induced Domain States of the Relaxor Ferroelectric PbMg1/3Nb2/3O3“,
Phys. Rev. Lett. 68, 847 (1992)
8
P. Lehnen, E. Beckers, „Ferroelectric Domains In the uniaxial relaxor System
SBN:Ce, Cr and Co“, Ferroelectrics, (eingereicht)
9
P. Lehnen, W. Kleemann, Th. Woike und R. Pankrath, „Phase Transitions in
Sr0.61Ba0.39Nb2O6:Ce3+: II. Linear birefringence studies of spontaneous and precursor
polarisation“, Eur. Phys. J. B 14, 633 (2000)
10
G. A. Smolenskii, V. A. Isupov, Dokl. Akad. Nauk SSSR 9, 653 (1954).
11
J. Dec, W. Kleemann, Th. Woike and R. Pankrath, „Phase Transitions in
Sr0.61Ba0.39Nb2O6:Ce3+: I. Susceptibility of clusters and domains“, Eur. Phys. J. B 14,
627 (2000)
12
K. Megumi, N. Nagatsuma, K. Kashiwada, Y. Furuhata, „. The congruent melting
composition of strontium barium niobate“, Mater. Sci. 11, 1583 (1976)
13
J. Bricmont, A. Kupiainen , „Lower critical dimension for the random-field Ising
model“, Phys. Rev. Lett. 59, 1829 (1987)
14
R. Lindner, „Kristalloptische Untersuchungen an den ungeordneten polaren
Systemen SrTiO3:Ca und PbMg1/3Nb2/3O3“, Diplomarbeit, (1996)
66
15
M. Aillerie, F. Abdi, M. D. Fontana, N. Théofanous, E. Abarkan, „Accurate
measurements of the electro-optic coefficients and birefringence changes using an
external modulation signal“, Rev. Sci. Instrum. 71, (2000)
16
P. S. Theocaris, E. E. Gdoutos, Springer Series in Optical Sciences 11, „Matrix
theory of Photoelasticity“, Springer (1979).
17
M. Zimmermann, W. Schranz, „A hybrid apparatus for automatic birefringence
measurements“, Meas. Sci. Technol. 4, 186 (1993)
18
D. Kip, S. Aulkemeyer, K. Buse, F. Mersch, R. Pankrath und E. Krätzig,
„Refractive indices of Sr0.61Ba0.39Nb2O6 Single Crystals“, Phys. Stat. Sol. (a) 154, K5
(1996)
19
L. E. Cross, „Relaxor Ferroelectrics“, Ferroelectrics 76, 241 (1987)
20
J. F. Nye, „Physical Properties of Crystals“, Oxford University Press, (1960)
21
W. Kleemann, F. Schäfer, M. Fontana, „Crystal optical studies of spontaneous and
precursor polarization in KnbO3 “, Phys. Rev. B 30, 1148 (1984)
22
J. R. Oliver, R. R. Neurgaonkar, „A thermodynamic phenomenology for
ferroelectric tungsten bronze Sr0.6Ba0.4Nb2O6 (SBN:60)“, J. Appl. Phys. 64, 32
(1988)
23
Y. Xu, Z. Li, W. Li und H. Wang, „Phasetransitions of some ferroelectric niobate
crystals with tungsten-bronze structure at low temperatures“, Am. Phys. Soc. 40,
11902 (1989)
24
M. E. J. Newman und G. T. Barkema, „Monte Carlo Study of the random-field
Ising model“, Phys. Rev. E 53, 393 (1996)
25
P. Lehnen, W. Kleemann, „Ferroelectric nanodomains in the uniaxial relaxor
system SBN“, Phys. Rev. B (eingereicht)
26
27
Zitat P. Lehnen (pers. Mitteilung)
T. Woike, T. Volk, U. Dörfler, R. Pankrath, L. Ivleva, M. Wöhlecke,
„Ferroelectric and optical Hysteresis in SBN doped rare-earth elements“,
Ferroelectric Letters 23, 127 (1998)
28
T. Granzow, U. Dörfler und Th. Woike, „Influence of Pinning Effects on the
Ferroelectric Hysteresis in Cerium-doped Strontium-Barium-Niobate“, Phys. Rev. B
(eingereicht)
67
29
G. Schmidt, G. Borchhardt, J. von Cieminski und D. Grützmann,
„Electromechanical properties of ferroelectrics with diffuse phase transition“,
Ferroelectrics 42, 3 (1982)
30
A. A. Berenzhnoi, M. F. Dubovik, Yu. V. Popov und T. N. Sherstneva, „Special
features of the electrooptical properties of strontium barium niobate crystals“, Opt.
Spektrosk. 46, 104 (1979)
31
Y. G. Wang, W. Kleemann, „Atomic force microscopy of Domains and volume
holograms in Sr0.61Ba0.39Nb2O6:Ce3+“, Phys. Rev. B 61, 3333 (2000)
32
Laser Handbook 1, edited by F. T. Arecchi, E. O. Schulz-Dubois, North-Holland
publishing company (Amsterdam, New York, Oxford), (1972), p. 1002
33
T. Granzow, „Dynamik und Pinning der ferroelektrischen Domänen im Relaxor-
Ferroelektrikum Sr0.61Ba0.39Nb2O6“, Diplomarbeit, Universität zu Köln, (1999)
68