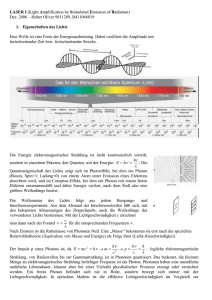
Optokommunikation
Werbung

Optokommunikation Skript Vorlesung und Übung Inhaltsverzeichnis 1. 2. 3. Maxwellsche Gleichungen ................................................................................................. 4 1.1 Elektrische und magnetische Felder ............................................................................ 4 1.2 Induktion ...................................................................................................................... 5 1.3 Kreisfrequenz und Wellenzahl .................................................................................... 6 1.4 Elektromagnetische Wellen im Vakuum ..................................................................... 6 1.5 Elektromagnetische Wellen in Materie ....................................................................... 7 1.6 Pointing Vektor.......................................................................................................... 10 1.7 Wellenpakete-Dispersion........................................................................................... 10 Metallische Wellenleiter .................................................................................................. 12 2.1 Metallische Röhre ...................................................................................................... 12 2.2 Wellenausbreitung zwischen 2 Metallflächen ........................................................... 13 Dielektrische Wellenleiter ................................................................................................ 15 3.1 3.1.1 Akzeptanzwinkel, Numerische Apertur und Totalreflektion ............................. 15 3.1.2 Moden................................................................................................................. 16 3.2 4. Grundlagen ................................................................................................................ 15 Glasfaserarten ............................................................................................................ 19 3.2.1 Stufenprofil......................................................................................................... 19 3.2.2 Gradientenprofil ................................................................................................. 19 3.2.3 Multimode Faser ................................................................................................ 19 3.2.4 Singlemode Faser ............................................................................................... 20 3.2.5 Aufgaben ............................................................................................................ 20 3.3 Dämpfung in Glasfaserwellenleitern ......................................................................... 21 3.4 Dispersion .................................................................................................................. 22 3.4.1 Modendispersion ................................................................................................ 22 3.4.2 Dispersionskoeffizient ........................................................................................ 23 3.4.3 Materialdispersion .............................................................................................. 23 3.4.4 Wellenleiterdispersion ........................................................................................ 24 3.4.5 Profildispersion .................................................................................................. 24 3.4.6 Gesamtdispersion ............................................................................................... 24 3.4.7 Gegenmaßnahmen .............................................................................................. 25 Übertragungssystem ......................................................................................................... 26 4.1 Lichtabsorption und -emission .................................................................................. 26 4.2 Sender ........................................................................................................................ 28 4.2.1 LED .................................................................................................................... 28 4.2.2 LD (Laserdiode) ................................................................................................. 29 2 4.2.3 4.3 Aufgaben ............................................................................................................ 30 Pumpen ...................................................................................................................... 32 4.3.1 Optisches Pumpen .............................................................................................. 32 4.3.2 Elektronisches Pumpen ...................................................................................... 33 4.4 Modulation................................................................................................................. 34 4.4.1 Direkte Modulation ............................................................................................ 34 4.4.2 Indirekte Modulation .......................................................................................... 34 4.4.3 Modulatoren ....................................................................................................... 34 4.5 Verstärker .................................................................................................................. 35 4.5.1 4.6 Erbium-Laser (EDFA, Faserlaser) ..................................................................... 35 Koppler ...................................................................................................................... 35 4.6.1 Richtkoppler ....................................................................................................... 35 4.6.2 Ringkoppler ........................................................................................................ 36 3 1. Maxwellsche Gleichungen 1.1 Elektrische und magnetische Felder Elektrische Flussdichte (Divergenz) mit als Polarisierung Elektrisches Feld hat Quellen und Senken. Quelle Senke wenn mehr raus geht als rein wenn mehr rein geht als raus φ1 + +- +- φ +- 2 +- ++- +E, D H, B Innerhalb Kondensator Polarisation der Materie. Im Leiter selbst nur sehr kleine Feldstärke. Elektrisches Feld erzeugt magnetisches Feld. Aufbau und Abbau des E-Feldes durch Verschiebungsstrom . Keine Teilchen, keine frei beweglichen Ladungsträger, sondern Energietransport über eine Art EM-Welle. Meist , keine Berücksichtigung der magnetischen Materialkonstanten. Keine Quellen und Senken im Magnetfeld. 4 Ein Strom erzeugt ein Magnetfeld. Gesamtstrom ergibt sich aus elektrischen und Verschiebungsstrom. H D Umfang Lg Fläche Aq In Glasfaser ist kein elektrischer Strom und somit kein : Fasst Lambertsches Gesetz zusammen. 1.2 Induktion Magnetisches Feld durch Leiterschleife erzeugt Strom. Genutzt bei Transformator und Generator. B induzierter i Strom Der erzeugte Strom wirkt der Ursache seines Entstehens entgegen → erzeugt Magnetfeld in entgegengesetzte Richtung. mit χ als spezifische elektrische Leitfähigkeit Sich veränderndes Feld induziert Feld. Feldgrößen hängen zusammen. Eine Veränderung der einen, bewirkt Änderung der anderen. 5 1.3 Kreisfrequenz und Wellenzahl Kreisfrequenz Wellenzahl 1.4 Elektromagnetische Wellen im Vakuum mit der Regel: Wellengleichung Vakuum ist das ideale Medium, da keine Verzerrungen und keine Störungen Formel 1-1 mögliche Lösung: Wenn man beide Ableitungen in Gleichung Formel 1-1 einsetzt, ergibt sich 0 → U ist eine Lösung dieser Gleichung. g f x Gleichung für eine Welle: 6 Überprüfen, ob diese Gleichung mögliche Lösung der Wellengleichung ist: Lösung für vorwärts und rückwärts laufende Welle → Dispersionsrelation im Vakuum Gruppengeschwindigkeit Phasengeschwindigkeit vg vp 1.5 Elektromagnetische Wellen in Materie Elektronen können auch so stark gebunden sein, dass keine Polarisation möglich ist. Induzierte Dipole treten bei E-Feld auf: Trennung der Ladungen Durch Polarisation erhöht sich zur Verfügung stehende elektrische Ladung. 7 Fouriertransformation einer Faltung ist eine Multiplikation. Im Material ändern sich c (sinkt) und k (steigt, λ sinkt). ω ist konstant. Dispersion durch Frequenzabhängigkeit des Materials (Geschwindigkeit abhängig von Frequenz). Fouriertransformation Bei Fouriertransformation transformiert. oder Wellenzahl mit 8 , je nachdem wonach man zweifache Ableitung nach dem Weg Gleichung gilt für eine Frequenz. Für jede Frequenz neu berechnen. Vorher im Vakuum galt Gleichung für gesamten Frequenzraum. Mit der Gleichung: Phasengeschwindigkeit: Brechzahl von ω abhängig, da auch εr und µr von ω abhängig im Vakuum ω reale Welle mit Verzerrungen ideal vp=vg k bei TE: bei TM: und immer senkrecht zueinander. km θm κ 90°-θm z nm nk Ex(y) βm z Ebene Welle mit räumlich harmonischem Verlauf. TE: normierte Wellenausbreitung in z 9 Ex abhängig von y An Grenzfläche tangentiale Komponente. Ex bleibt gleich. Senkrechte Komponenten nicht gleich: wenn Über gelangt man zu Hy und Hz. Ex H z 1.6 Pointing Vektor Komplexer Pointing Vektor 1.7 Wellenpakete-Dispersion 1D: Spezialfall in Vakuum Gleichung entspricht ungestörtem Wellenpaket nach rechts mit Geschwindigkeit c0 laufend. Gleichung erklärt sich, wenn man den Wellenberg betrachtet. Wenn t größer wird, muss auch x größer werden, um relativ gleich zum betrachteten Wellenstück von x=0, t=0 zu bleiben. Ein größeres x bedeutet, dass die Welle mit zunehmender Zeit nach rechts wandert. 10 Taylor-Entwicklung: Erste Ableitung (Gruppengeschwindigkeit) ist für Modulation (Information), Störung → verzerrt modulierte Welle. Wenn keine Verzerrungen. 11 ist 2. Metallische Wellenleiter 2.1 Metallische Röhre mit reflektierender Innenseite y z r x variiert nur in x und y Richtung Eigenwerte von berechnen. Lösungen der Gleichungen sind die Moden. Je Eigenwert eine Lösung. 12 ω jede Kurve eine Mode Kurve nähert sich dem Grenzfall c0·β c0 k r3 c0 k r2 c0 k r1 Cut-Off Frequenz β Jede Mode hat andere Ausbreitungserscheinungen (Geschwindigkeit). Je höher Frequenz (ω), desto mehr Moden → schlechter → niedrige Frequenz mit nur einen Mode nutzen. Modendispersion: Moden kommen unterschiedlich an und stören Detektion. Eigenfunktionen: 2.2 Wellenausbreitung zwischen 2 Metallflächen unendlich ausgedehnte Platten Wellen breiten sich nicht nur nach vorne aus, sondern werden auch zurückreflektiert. Wellen müssen sich konstruktiv überlagern. B A λ θ d θ original Welle k zweifach reflektierte C Welle kym βm 13 ω m 2 c0·k0 im Vakuum m 1 2c0 m 0 c0 d Cut-Off Frequenz d βm Alles unter Cut-Off Frequenz wird zurückreflektiert. Gruppengeschwindigkeit vg c0 m=1 jede Kurve eine Mode βm 14 3. Dielektrische Wellenleiter 3.1 Grundlagen Wellenfronten Durch optischen Wellenleiter gehen nur Wellen, die hineinpassen. Andere werden reflektiert und kommen am Anfang wieder hinaus (anderen Eintrittswinkel wählen je nach Wellenlänge). Zur Übertragung wird Totalreflektion genutzt. Glasfaser (dielektrischer Wellenleiter) besser als metallische Wellenleiter, wegen geringerer Dämpfung. Bei dielektrischen Wellenleitern dringt Feld der Welle ins Material ein wenig ein, bei metallischen nicht. EM-Wellen treten erst ab sehr hohen Frequenzen (Röntgenstrahlen) ins Metall ein. Metallischer Dielektrischer Wellenleiter In dielektrischen Wellenleitern gehen alle Frequenzen durch, keine Cut-Off Frequenz wie bei metallischen Wellenleitern. 3.1.1 Akzeptanzwinkel, Numerische Apertur und Totalreflektion nm nm β α nk nAußen φA φg nk Bei Totalreflexion ist und der Grenzwinkel. Für alle Winkel α größer gleich dem Grenzwinkel ist Totalreflexion möglich. Numerische Apertur Akzeptanzwinkel, maximaler Winkel am Eingang. Wenn Eintrittswinkel von Außen zu groß wird, ist α kleiner als φg und somit keine Totalreflexion möglich. φg einsetzen und lange umformen: 15 Für Luft 3.1.2 . Moden Moden sind mögliche Eintrittswinkel mit konstruktiver Interferenz. Keine beliebigen Winkel möglich. Restliches Licht wird vorne wieder zurückgestrahlt → Energie verschwindet nicht. B θθ B kk 2θ A d=2a A θθ θ C C Strahl muss für konstruktive Überlagerung in Phase mit Wellenfront sein. Bei Reflektion an Grenzflächen kommt es zur Phasenverschiebung, Verschiebung der Wellenfronten. Strecke von A bis C: ohne Auslöschung erwünscht: mit Auslöschung unerwünscht: Berechnung der Strecke: mit: Winkel der Mode i) Vernachlässigung des Phasensprungs an Grenzfläche Gilt in diesem speziellen Fall. Zusätzlich auch . Für gute Leitung/ viele Moden werden benötigt: große Dicke, kleine Wellenlängen, große Brechzahl im Kern. ii) Mit Betrachtung des Phasensprungs Fressnel Gleichung für transversal elektrisch polarisierte Welle: θ’m in nm 16 Fressnel Gleichung für transversal magnetisch polarisierte Welle: Wir wollen nun Brechgesetz: ersetzen Wurzel wird negativ bei Totalreflektion Beispiel: mit und wir wählen –j… als Lösung kaum Phasenverschiebung mit : starke Phasenverschiebung mit : , Feld dreht sich fast um Anmerkung: Es gibt nur Phasenverschiebungen zwischen 0 und 180°. Einfallswinkel muss größer sein als . Eindringtiefe: Durch das Eindringen Verschiebung der Reflexionspunkte. 17 … Nach auflösen. Numerische oder grafische Lösungsverfahren (vorher auf beiden Seiten den Tangens nehmen). mögliche Lösungen für Moden: Für schwach führende Leitung ( ) gibt es wesentlich weniger Lösungen. Zu jeder Mode eine bestimmte Feldverteilung. Normierung: Konstante, abhängig vom verwendeten Material transversaler Anteil (senkrecht zur Ausbreitungsrichtung) → U, V, W in TE und TM Gleichung einsetzen TE-Polarisation: Mantel nm Kern nk θm k km κm (Kappa) βm 18 TM-Polarisation: a·ky a·km θ 0 Grundmode a k k m andere Modi a k k a·ky a a θg θm a·kz V m U m a·kz a·kk Es muss immer gelten trifft. . 3.2 Glasfaserarten 3.2.1 Stufenprofil ist kleinstmöglicher Winkel, wenn Strahl auf Grenzfläche Kern besitzt einheitliche Brechzahl. Abrupter Übergang vom Kern zum Mantel. nM nM < nK 3.2.2 nK Gradientenprofil Kern besitzt mehrere Schichten Glas mit nach außen abnehmender Brechzahl. Dadurch werden Strahlen außen schneller transportiert als innen und Laufzeitunterschiede zwischen Moden ausgeglichen. 3.2.3 Multimode Faser Leitet mehrere Moden durch, die sich gegenseitig stören (Modendispersion) und die Detektion des Signals am Ausgang erschweren. Jede Mode hat eigenen Eintrittswinkel. Anzahl der möglichen Moden durch Frequenz (Wellenlänge) und Querschnitt bestimmt. Je höher Frequenz und je größer Querschnitt, desto mehr Moden werden geleitet. 19 Multimode Fasern gibt es sowohl im Stufen- als auch Gradientenprofil. Eignet sich nur für kurze Strecken, ist aber wegen des größeren Durchmessers und der einfacheren Montage billiger. Leistung wird in Bitrate mal Länge = Bitratenlängenprodukt angegeben. Für Multimode beträgt Produkt etwa . 3.2.4 Singlemode Faser Nur als Stufenprofil. Da nur eine Mode geleitet wird, wäre Gradientenprofil überflüssig. Weniger Dispersion als Multimode. Singlemode durch sehr kleinen Durchmesser (6µm) erreicht. Dadurch große Strecken (Bitratenlängenprodukt: ) möglich. Teuer durch kleinen Durchmesser (6µm) und sehr genaue Montage. 3.2.5 Aufgaben 3.2.5.1 OWL1 Ein FWL (Faserwellenleiter) für Mehrmodenausbreitung mit Stufenprofil hat eine Numerische Apertur (NA) zu Luft von 0,3 und einen Brechungsindex im Mantel von . a) Wie groß ist der Akzeptanzwinkel φA des FWL in Wasser, wenn dessen Brechungsindex ist? Vergleichen sie diesen mit dem üblichen Akzeptanzwinkel! In Luft: Brechzahl von Glas gewöhnlich zwischen 1,4 und 1,8. Akzeptanzwinkel ist etwa 5° kleiner. b) Berechnen sie den Grenzwinkel φg an der Grenzfläche Kern-Mantel, ab dem Totalreflektion auftritt! 3.2.5.2 OWL2 In einem FWL für Mehrmodenausbreitung mit Stufenprofil breitet sich ein Strahl mit einer Geschwindigkeit von aus und der Grenzwinkel an der Grenzfläche KernMantel beträgt 80°. Berechnen sie den Akzeptanzwinkel φA des FWL, wenn sich dieser in Luft befindet! 20 3.2.5.3 OWL3 Ein planarer Schichtwellenleiter (SWL, Dicke << Breite) mit symmetrischem Aufbau soll durch einen HeNe-Laser ( ) angeregt werden. Berechnen sie für folgende Fälle die Zahl der sich ausbreitenden Moden: a) Die wellenführende Schicht besteht aus Glas mit konstantem Brechungsindex , hat eine Dicke und ist von Luft ( ) umgeben! Maximale Anzahl der Moden: Modenzahl Nicht festgelegt, ob auf- oder abgerundet wird. Beispiel: 100facher Durchmesser → 100 mal so viele Moden/Wege. b) Die gleiche wellenführende Schicht (s.a.) ist auf der Ober- und Unterseite jeweils durch eine Glasschicht mit begrenzt! Schwach führender Fall . Je höher λ, desto weniger Moden, bis hin zu Singlemode ( für a) bei für b) bei 3.3 Dämpfung in Glasfaserwellenleitern Dämpfungsfaktor z=0 z P(0) P(z) , Dimension: 21 ). Tritt ein: gute Glasfasern z.B. mit mit Dämpfung durch Streuung, Absorption, austretende Wellen, Strahlführung. Streuung: Bei Ungleichmäßigkeiten im Material entstehen neue Wellen in andere Richtungen. Strahlführung: Bei gekrümmten Wellenleitern werden Wellen in einer Kurve aus dem Wellenleiter herausgetragen Dämpfungsminima bei den Wellenlängen 1,55µm, 1,3µm und 0,75-0,9µm. Deshalb sind diese Wellenlängen besonders interessant bei Nutzung. 3.4 Dispersion Verzerrung der Informationsimpulse 3.4.1 Modendispersion Tritt auf, weil Moden unterschiedliche Weglängen und somit Laufzeit haben. Überlagern sich am Ausgang und erschweren Detektion. Stellt den größten Anteil der Gesamtdispersion bei Multimode Wellenleitern. a θc Mantel nm Kern nk θ t0 θc b tc L kritischer Winkel bei Totalreflektion Zeit für geraden Strahl Zeit für schrägen Strahl mit kritischem Winkel 22 Je größer Trägerfrequenz (je kleiner Wellenlänge: 850, 1300, 1550nm), desto kleiner Wellenlängenverschiebung. Je größer modulierende Frequenz (1 – 1000GHz), desto größer Wellenlängenverschiebung. Große Wellenlängenverschiebungen schlecht, stören eventuell Nachbarsignalrückerkennung, da Bits ineinander laufen, verschmieren. 3.4.2 Dispersionskoeffizient δτd τd τd+δt Dispersionskoeffizient: Picosekunden pro (Nanometer mal Kilometer) 3.4.3 Materialdispersion Brechzahl abhängig von Frequenz. Deshalb werden Wellen unterschiedlicher Frequenz unterschiedlich schnell geleitet. Bits laufen ineinander, verschmieren (wie bei Modendispersion). 23 3.4.4 Wellenleiterdispersion Welle tritt kurz in Mantel ein (real), statt Totalreflektion (ideal). Auch bei zu engen Kurven kann Licht aus Wellenleiter austreten. Da Mantel aber viel geringere Brechzahl hat als Kern, wird Licht darin wesentlich schneller geleitet. Auch die Eindringtiefe hängt von der Wellenlänge ab. Mantel Kern Mantel W Intensität für niedrige Frequenzen Intensität für hohe Frequenzen 3.4.5 K Profildispersion Enthält Änderung des Brechzahlprofils mit der Frequenz. 3.4.6 Gesamtdispersion Für Singlemode gibt es keine Modendispersion: Bei Multimode ist die Modendispersion so dominant, dass andere vernachlässigbar. 24 3.4.7 Gegenmaßnahmen Anpassen des Brechzahlprofils des Wellenleiters damit Dispersion Minimum bei Übertragungsfrequenz. n D λ 0 a Brechzahlverlauf über Querschnitt Wellenleiterdispersion + Materialdispersion = Chromatische Dispersion. Gewöhnlich 0 bei . Durch Gegenmaßnahmen kann man dies ins Dämpfungsminimum bei 1550nm bringen. Die Dispersion, die durch die frequenzabhängige Brechzahl der Wellenleiter entsteht, kann eliminiert werden, indem nach einem Stück Wellenleiter mit bestimmten Brechzahlverhalten ein anderes mit genau entgegengesetzten Verhalten folgt. 25 4. Übertragungssystem Quelle Sender Empfänger Senke Sender = Elektrisch-Optische Wandler Empfänger = Optisch-Elektrische Wandler 4.1 Lichtabsorption und -emission W W GaAs K direkte Halbleiter Absorption - Si, Ge K indirekte Halbleiter spontane Emission - stimulierte Emission - ELeitband ES - - EL EV EValenzband - Aus Bandabstand kann man emittierte Wellenlänge ermitteln. Wenn man Stromstärke durch Diode ändert, ändern sich auch die Energieniveaus der einströmenden Elektronen. Je größer I, desto größer Banddifferenz und Energie, desto größer Frequenz, desto kleiner Wellenlänge. Je größer Temperatur, desto kleiner Banddifferenz und Energie, desto kleiner Frequenz und desto größer Wellenlänge. Bei Emission wird nicht nur genau eine einzige Wellenlänge ausgestrahlt, da Elektronen eine Verteilungsfunktion besitzen. WLeit - - Verteilungsfunktion der Elektronen Verteilungsfunktion bei höherem I WValenz - 26 spontane Emission: Licht emittiert durch zufällige Rekombination, Zeitpunkt nicht genau bestimmbar Absorption des Lichts im Sender wirkt sich störend aus → induzierte Absorption, Generation eines Elektronen-Loch-Paares EPhoton bei Silizium etwa 1,12V induzierte/ stimulierte Emission: auf schon erregtes Elektron trifft Licht und es wird zweites Photon mit gleicher Wellenlänge und Phase erzeugt für bestimmte Wellenlängen Bandabstände variieren, Mischhalbleiter im Grundzustand können keine Emission abgeben werden. Emission einer Mode Amplitude drückt Anzahl der Photonen. Bei Emission wird Amplitude größer. Bei Absorption kleiner. Photon ħω 20% Einfallendes und reflektiertes Licht löschen sich idealerweise aus und verstärken so durchgehendes Licht bis auf das 5 fache der Intensität der einfallenden Strahlung. 80% 80% 20% Besetzungszahlen Inversion Q = Anzahl der Photonen Bilanzgleichungen welche Prozesse Photonenanzahl erhöhen oder verringern. Absorption: → wenn oben mehr werden, dann müssen unten weniger werden. Bei Absorption sinkt Q Absorption - 1,5 ħω Emission - E2, N2 . Abgabe nur in ganzen Paketen. ½ ħω - - E1, N1 spontane Emission: stimulierte Emission: Gesamt: 27 B12, B21 = B Einsteinkoeffizienten, gleiche Wahrscheinlichkeit für beide Prozesse Q0 = Vakuumfluktuation im Grundzustand κ = Verlust, von Apertur abhängig Q ist unbekannt Inversion (wenn = 0, dann oben genauso viele Elektronen wie unten) Rest bekannt Bei Laser ist AN2 sehr klein. Bei LED ist AN2 sehr groß. Durch Verluste würde System irgendwann in Ruhezustand kommen. Damit (bei Laser) Inversion erhöhen → N2 vergrößern (Elektronen hoch bringen), durch: optisches Pumpen elektronisches Pumpen 4.2 Sender An Dioden Rechtecksignal angelegt. Optische Leistung Popt und Intensität nach Zeit moduliert. Sendedioden sind in Durchlassrichtung gepolt. Empfangsdioden in Sperrrichtung gepolt, um die Spannungsänderung über ihnen, verursacht durch den Lichteinfall zu messen. 4.2.1 LED eingesetzt bei Multimode breites Spektrum besteht aus einer n- und einer p-dotierten Zone, zwischen beiden bildet sich eine Raumladungszone nicht interferenzfähig (Photonen kommen zufällig, statistische Verteilung), spontane Emission durch Rekombination in Raumladungszone verschiedene Moden interferenzfähig, damit nicht so störungsanfällig weiße Dioden über 3 Dioden (RGB) oder UV-Diode mit Phosphor → Phosphor macht aus UV sichtbares Licht mit breitem Spektrum n p - - - Licht Fermienergie +++ hohe Konzentration der Ladungsträger in Raumladungszone, dort größte Strahlungsintensität Elektronenbewegung in Bahngebiete durch Diffusion, in Raumladungszone durch elektrisches Feld Licht sollte vor Absorption die Raumladungszone nach außen verlassen damit es außerhalb der Raumladungszone zu keiner unerwünschten Rekombination kommt, erhält RLZ höheren Brechungsindex und somit anderen Bandabstand als in Bahngebiete 28 W Elektronenenergie p RLZ n aktive Zone n Brechungsindex Flächenstrahler Kantenstrahler ganz dünne obere Schicht, damit Licht durch kommt 4.2.2 RLZ LD (Laserdiode) Eingesetzt bei Singlemode schmales Spektrum (kohärent, monochromatisches Licht gleicher Polarisation und Phase) interferenzfähig da kohärent anfällig gegen Störungen, die Kohärenz zerstören extrem hoch dotiert → Inversion, Ferminiveau rutscht in die Bänder spontan emittierte Photonen wichtig, damit Laser in Gang kommt, sie werden gesammelt (Rückkopplung der Photonen) bis stimulierte Emission einsetzt Rückkopplung der Photonen zwischen zwei Spiegel, Reflexionskoeffizient gefangene Photonen werden durch Filter aus dem Resonator nach außen gelassen Filter behält nur bestimmte Wellen (stehende Wellen mit bestimmter Wellenlänge, ) drin spontane Photonen würden in Verstärkern stören, deshalb werden sie herausgefiltert + Isolator p-AlGaAs hier geht Licht raus: 200nm GaAs aktives Gebiet n-AlGaAs 5µm n-GaAs Substrat 200µm durch geringe Schichtdicke (200nm) starke Beugung, divergentes Profil, mit Kugellinse versucht man es auszugleichen, bevor Licht in den Wellenleiter geschickt wird 29 4.2.3 Aufgaben 4.2.3.1 LED1 Berechnen sie für eine GaAs-LED die Wellenlänge der größten Strahlungsemission λP bei Zimmertemperatur (20°C)! a) Wie ändert sich λP bei einer Temperaturerhöhung auf 60°C? b) Diskutieren sie den Einfluss der Temperaturerhöhung auf die IU-Kennlinie und den Wirkungsgrad! Φ 20-50nm 867 λ 20 bis 50nm Änderung bei Temperaturschwankungen Bolzmannkonstante I U 4.2.3.2 LED2 Im Inneren einer LED mit Doppelheterostruktur (AlGaAs) wird bei einem Flussstrom von 60mA eine optische Leistung von 28,4mW erzeugt. a) Berechnen sie die Wellenlänge der größten Strahlungsemission λP, wenn die Lebensdauern für strahlende und nichtstrahlende Rekombination der Minoritäten gleich groß sind! b) Diskutieren sie den konstruktiven Widerspruch zwischen hohem Quantenwirkungsgrad und schneller Modulierbarkeit einer solchen LED! 4.2.3.3 LED3 Eine GaAs-Flächenemitterdiode emittiert bei einer Wellenlänge , hat einen inneren Quantenwirkungsgrad von 60% und wird von einem Flussstrom durchflossen. Bestimmen sie die durch Lumineszenz erzeugte innere optische Leistung! 30 Wirkungsgrad, Φe I 4.2.3.4 LD4 Eine GaAs-Injektions-Laserdiode habe unter normalen statischen Betriebsbedingungen einen Schwellenstrom , einen differentiellen Quantenwirkungsgrad ηd von 50%, wird von einem Strom durchflossen und emittiert optische Strahlung bei einer Peakwellenlänge von . a) Berechnen sie die emittierte optische Leistung! Schwellstrom fließender Strom + + N Phot t Wg - Photonen pro Zeit Bis IS nur spontane Emission, erst wenn der Strom über IS, werden induzierte Photonen erzeugt. Φe ab IS linearer Anstieg d e dI IS I Diskutieren sie den differentiellen Quantenwirkungsgrad ηd und den inneren Quantenwirkungsgrad ηi! Wirkungsgrad ist Verhältnis von erzeugten Photonen zu zugeführter Ladung. b) 31 4.2.3.5 LD5 Eine verstärkungsgeführte GaAs-Laserdiode sei auf einem Arbeitspunkt bei 5mW Leistungsabgabe bei eingestellt. Bei der Umgebungstemperatur sei der Schwellenstrom und der differentielle Quantenwirkungsgrad ηd betrage 30% (diodenabhängige Konstante ). Wie ändert sich die abgegebene Leistung, wenn sich im Betrieb die Umgebungstemperatur um 10K erhöht und der Gesamtstrom konstant bleibt? IS ist stark temperaturabhängig. Photodiode misst Φe und korrigiert I. Strom bestimmen: wenn I konstant, sinkt Φe auf ein Viertel 4.3 Pumpen 4.3.1 Optisches Pumpen 4-Niveau-Laser (vor allem Gaslaser) (es gibt auch 3-Niveau-Laser) - - - - Bilanzgeleichung für Elektronen: P = Pumpparameter, Anzahl der Elektronen pro Zeit (daran können wir drehen) Verluste durch Pumpvorgang (wenn Photonen erzeugt wird, geht Inversion um 2 Stellen runter) spontane Verluste Photonenlebensdauer Näherung = Adiabatische Approximation, d.h. nach n auflösen immer im Gleichgewicht Bei wächst Photonenzahl Q, aber da Q auch in Nenner, wird Zuwachs immer kleiner, wächst somit nicht ins Unendliche. 32 QStat Ph P 1 2 B Sp 2 P 1 Pth B Ph Sp Pth = Schwellwert für Pumpvorgang (möglichst klein für guten Laser). Für kleines P th große Lebensdauer τPh, τSp. 4.3.2 Elektronisches Pumpen n - - - - - - + + - p + + + Halbleiter mit n und p dotierten Hälften. Empfänger: undotierter Halbleiter ohne Licht Isolator, mit Licht schwach leitend Für Ladungsträgertransport entweder Spannung anlegen → abschrägen der Energieniveaus - + + Oder: p-n Dotierung, dann keine zusätzliche Spannung nötig, bei Solarzelle genutzt Für eine Mode: Dimension mit J = Stromdicht, d = Dicke der RLZ, e = Elementarladung, , C = Coulomb 33 (Doppelhetero-Strukturen, innen stärker dotiert als außen, über verschiedene Materialien realisiert, Rekombination hauptsächlich in RLZ) Streifenlaser: p p Photonen können nur an Stirnfläche austreten Isolator n 4.4 Modulation 4.4.1 Direkte Modulation Für geringe Modulationsfrequenzen wird direkt I durch Diode moduliert. Direkte Änderung der Strahlungsleistung. Hauptsächlich eingesetzt bei LED und Übertragungen über Multimodefasern. Datenraten , da LED träge. LED, (LD) moduliertes Signal iVerstärker iSignal LED modulierendes Signal 4.4.2 LD Indirekte Modulation Modulation Verstärker Detektor Signal Signal 4.4.3 Modulatoren Für hohe Modulationsfrequenzen (> 1GHz) wird Elektro-Absorptionsmodul benötigt, das die Leitfähigkeit/ Brechzahl so ändern, dass Signal moduliert raus kommt (≈ 10GHz). Mach-Zehnder-Interferometer Auslöschen (reflektieren, Signal kommt vorne wieder raus, geht nicht verloren) oder Verstärken. Nutzung des Pockets Effekt zur Veränderung des Brechungsindexes. Signal Akustischer Modulator 34 LD Surface Acoustic Waves, Schaltender Strahl 4.5 Verstärker 4.5.1 Erbium-Laser (EDFA, Faserlaser) 1 - 2 Signal - 3 - - dotiert undotiert Pumplaser 4 - Ein Stück Glasfaser (Siliziumdioxid, SiO2) ist mit Erbium (Er3+) dotiert. Durch gezielte Dotierung werden bestimmte Energieniveaus eingestellt (4 Niveaus), wodurch nur bestimmte Wellenlängen verstärkt werden (980, 1530nm). Im ersten Schritt wird ein Elektron auf ein höheres Energieniveau gepumpt. Auf diesem verweilt es nur kurz (Picosekunden) und fällt anschließend auf ein metastabiles Zwischenniveau (Verweilzeit mehrere Millisekunden). Kommt nun ein Lichtimpuls passender Wellenlänge an, wird das Elektron angeregt, ebenfalls einen Impuls mit gleichen Eigenschaften (kohärent) abzugeben. Somit induzierte Emission zur Verstärkung. Spontane Emission (Rekombination) ungewollt, sollte vermeidet werden. Ebenso ist das Absorbieren emittierter Photonen ungewünscht. Abschließend kehrt Elektron wieder in den Ursprungszustand zurück. Zur Anregung werden Photonen vom Empfänger rückgekoppelt. Zum dotieren sind alle Elemente der Lanthanoiden (Seltene Erden) geeignet. SiO2 transparentes Wirtsmaterial mit guter Isolation. Bei hohen Leistungen/ Übertragungsraten gibt es nichtlineare Effekte. 4.6 Koppler 4.6.1 Richtkoppler λ1 λ1+λ2 λ2 35 Zwei Signale werden auf eine Faser zusammengeführt. Gezieltes Ausnutzen des Übersprechens. Auch Auskoppeln möglich. 4.6.2 Ringkoppler ausgekoppelt Signal eingekoppelt Länge des Rings ist Vielfaches der Wellenlänge des Signals. 36