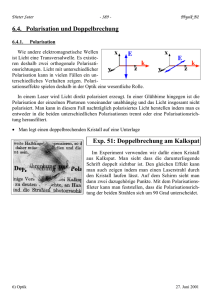
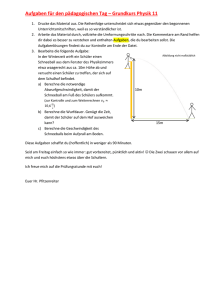
Analyse der spannungsinduzierten Doppelbrechung in

Analyse der spannungsinduzierten Doppelbrechung in
Laserkristallen und deren Einfluss auf Laserresonatoren
Der Technischen Fakultät
der Friedrich-Alexander-Universität
Erlangen-Nürnberg
zur
Erlangung des Doktorgrades Dr. Ing.
vorgelegt von
Thomas Graupeter
aus Leipzig
Als Dissertation genehmigt
von der Technischen Fakultät
der Friedrich-Alexander-Universität Erlangen-Nürnberg
Tag der mündlichen Prüfung: 2.4.2015
Vorsitzende des Promotionsorgans: Prof. Dr.-Ing. habil. Marion Merklein
Gutachter:
Prof. Dr. C. Pflaum
Prof. Dr. A. Otto
Danksagung
Viele Leute haben mich während meiner Jahre beim Lehrstuhl für Systemsimulation unterstüzt. Ihnen möchte ich hiermit meinen Dank aussprechen.
Am meisten möchte ich mich bei Prof. Dr. Christoph Pflaum für die jahrelange Betreuung und Unterstützung meines Promotionsvorhabens bedanken. Seine Geduld und Hilfen beim Erlernen der objektorientierten Programmierung und lasertechnischem Wissen haben meine Promotion erst möglich
gemacht. Auch danke ich ihm für meine Entwicklung zum selbstständigen Entscheiden und Verantworten.
Auch möchte ich meinen Mentor Dr. Rainer Engelbrecht meine tiefe Dankbarkeit ausdrücken. Er
brachte mir viele Grundlagen über Laser bei, da ich noch ohne Wissen darüber zum Lehrstuhl für
Systemsimulation kam.
Weiterer Dank gilt Prof. Dr. Paul Steinmann. Wenn mein Studiumswissen über technische Mechanik
mal nicht ausreichte, half er mir immer gerne weiter.
Auch danke ich meinem Kollegen Rainer Hartmann, welcher mein Arbeitszimmer für lange Zeit
teilte, wodurch wir effizient an Modellierung, Implementation, Simulation und Ergebnisauswertung
zusammen arbeiten konnten. Des Weiteren haben mir meine Arbeitskollegen unserer Arbeitsgruppe Kai Hertel, Christine Jandl, Shuai Yan und Birhanu Tamene Abebe sehr viel in verschiedenen
Bereichen wie Mathematik oder Unibürokratie geholfen, wofür ich mich ebenfalls bedanken will.
Spezieller Dank gilt meinen Vorgängern in der Lasersimulation am Lehrstuhl für Systemsimulation
Johannes Werner und Matthias Wohlmuth, welche mir viele Fakten und Tricks über die Simulationssoftware beibrachten.
Auch möchte ich mich für die Hilfe der Kollegen der Gruppe von Prof. Ulrich Rüde bedanken, bei
Dr. Harald Köstler und Markus Stürmer für die Hilfe bei Programmierung mit C++, bei den Mitarbeitern vom Lehrstuhl Iris Weiß, Gaby Fleig, Elzbieta Beetz und Heike Strohm für die Hilfe bei
bürokratischen Problemen und besonders bei Frank Deserno, welcher bei EDV-technischen, administrativen und werkstofftechnischen Problemen immer eine sehr große Hilfe war.
Ich möchte auch den Kollegen Dr. Dubravka Melling, Dr. Jürgen Großmann, Christina Ort und Joana
Stmpfig Barrinho vom SAOT-Programm für die finanzielle Unterstützung bei den Konferenzen und
für die umfangreiche Ausbildung in Optik in den Akademien und Workshops danken. Auch danke
ich den SAOT-Mitgliedern Maik Zimmermann und Wolfgang Iff für die Hilfe in Optik- und Laserfragen.
Weiterer Dank geht an Christian Kipplinger und Jörg Hurich von der A.R.C. Laser GmbH für die
sehr gute Zusammenarbeit im Projekt Berechnungsprogramm für innovative Kurzpulslaser mit pas”
sivem Q-Switch“. Diese Unternehmung war sehr interessant und gab mir viel technisches Wissen
über Laserdesign und Laserexperimente.
Auch geht mein Dank an meine Familie und besonders an meine Eltern für ihre Unterstützung, geduldige Erziehung und Förderung über Jahrzehnte.
Spezieller Dank geht an meinen Opa Lothar Pester für das Probelesen meiner Dissertation und die
vielen Hilfe im Bereich der Kristallphysik.
0.1 Kurzzusammenfassung
In dieser vorliegenden Dissertation wird mit Hilfe von numerischen Simulationen der Einfluss der
spannungsinduzierten Doppelbrechung auf die Eigenpolarisationszustände von Festkörperlasern untersucht. Es werden die grundlegenden physikalischen Zusammenhänge zwischen den thermischen,
mechanischen und elektromagnetischen Feldern behandelt, die durch die nicht homogen verteilte
Absorption des Pumplichtes im Laserkristall auftreten. Die durch diesen photoelastischen Effekt dominierten Eigenpolarisationszustände im Resonator werden untersucht. Als eine Anwendung werden die Eigenpolarisationszustände, die Ausgangsleistung, die Strahlqualität und die Polarisationsreinheit eines Laserresonators mit Brewsterplatten in Abhängigkeit von den Kristallschnitten des
Nd:YAG-Laserkristalls erforscht. In einem zweiten Beispiel wird mit Hilfe des polarisationsabhängigen Stabilitätsverhaltens eines Laserresonators mit einem Nd:YAG-Kristall ein Ausgangsstrahl einer
bestimmten zirkularen Polarisation ohne zusätzliche optische Elemente erzeugt. Dabei wird ebenfalls
der Einfluss der Kristallschnitte auf die Stabilitätsbereiche, die Ausgangsleistung und die Strahlqualität untersucht.
Kapitel 2 befasst sich mit den physikalischen Grundlagen der Mechanik und Optik, welche in dieser
Arbeit angewendet werden. Dabei wird ein Überblick über verschiedene Festkörperlasermaterialen
und deren Einteilung in Kristallklassen gegeben. Es wird auf die Modellierung des mechanischen
Steifigkeitsverhaltens des Kristalls mit Hilfe von anisotropen und isotropen Materialmodellen eingegangen. Als weiterer physikalischer Effekt im Kristall wird die Kopplung zwischen den mechanischen und optischen Feldern sowie deren mathematische Handhabung beschrieben.
Kapitel 3 behandelt die Eigenpolarisationszustände in Festkörperlaserresonatoren mit Nd:YAG-Kristallen aufgrund thermisch induzierter Doppelbrechung. Es wird darin auf Eigenpolarisationszustände
im Resonator und ihre Berechnung durch den Jonesformalismus eingegangen. Die Eigenmoden des
elektromagnetischen Feldes innerhalb eines Resonators werden kurz erwähnt. Für die Berechnung
der Ausgangsleistung und Strahlqualität eines Resonators wird die Dynamische Multimode Analyse kurz vorgestellt. Um mögliche Stabilitätsuntersuchungen von Festkörperlasern durchführen zu
können, wird der parabolische Fit der Brechungsindizes, die ABCD-Matrixmethode und der polarisationsabhängige Brechungsindex mit dessen Auswirkung auf die Resonatorstabilität beschrieben.
Im Kapitel 4 wird eine Untersuchung zur Verbesserung der Strahlqualität und Ausgangsleistung
durch Verwendung eines Polarisationsfilters in einem Resonator mit einem Nd:YAG-Kristall durchgeführt. Darin werden nach dem Vorstellen des numerischen Modells die auftretende Temperaturverteilung und die auftretenden mechanischen Spannungen im Kristall aufgrund des absorbierten Pumplichtes dargestellt. Anschließend wird die spannungsinduzierte Doppelbrechung gezeigt. Die resultierenden Eigenpolarisationszustände im Resonator mit und ohne Brewsterplatten werden mit dem
Jonesformalismus berechnet. Abschließend werden die erzielten Ausgangsleistungen, die Strahlqualität und die Polarisationsreinheit in Abhängigkeit von den Kristallschnittrichtungen verglichen. Dabei werden der [100]-Schnitt mit einer Rotation des Kristalls um seine eigene Längsachse um 0◦ und
90◦ , der [110]-Schnitt mit einer Rotation um 0◦ , 45◦ und 90◦ und der [111]-Schnitt ohne Variation
des Rotationswinkels betrachtet.
Ein Beispiel zur Erzeugung eines bestimmten Polarisationszustandes mittels unterschiedlichen Stabilitätsverhalten durch spannungsinduzierte Doppelbrechung im Resonator wird im Kapitel 5 gezeigt. Dazu werden nach dem Vorstellen des zugrunde liegenden Modells der Temperaturverlauf
und die auftretenden mechanischen Spannungen im Kristall untersucht. Des Weiteren werden die
resultierenden, von der Schnittrichtung des Kristalls abhängige Brechungsindizes und Doppelbre-
1
chungsmuster berechnet. Dabei werden die Schnittrichtungen und Rotationen des Laserkristalls wie
im vorhergehenden Kapitel variiert. Es werden die auftretenden Eigenmodeprofile gezeigt. Durch die
unterschiedliche Ausprägung der Doppelbrechung entstehen bei Variation der Länge des Resonators
bestimmte Bereiche, in denen nur der radiale oder nur der azimutale Eigenpolarisationszustand stabil
ist. Diese Bereiche werden in Abhängigkeit vom Kristallschnitt und -drehung quantitativ berechnet.
In diesen Bereichen werden die Strahlradien der Eigenmoden der ersten Ordnung, die Ausgangsleistung und die Strahlqualität ermittelt und miteinander verglichen.
Im letzten Kapitel 6 werden abschließend die Erkenntnisse dieser Arbeit zusammengefasst, auf Einschränkungen der erzielten Ergebnisse eingegangen und ein möglicher Ausblick gezeigt.
Zusammenfassend lässt sich aussagen, dass sich mit Hilfe dieser numerischen Methoden genaue
Analysen der Eigenpolarisationszustände in einem Festkörperlaserresonator aufgrund der spannungsinduzierten Doppelbrechung durchführen lassen, was mit den bisherigen auf analytischen Formeln
aufbauenden Methoden nur eingeschränkt oder gar nicht möglich war. Mit den hier vorgestellten
Methoden lassen sich effektiv Laserresonatoren simulieren und entwickeln, welche bestimmte Polarisationseigenschaften aufweisen sollen.
2
0.2 Abstract
This dissertation investigates the influence of stress induced birefringence on the eigenpolarization
states of solid state lasers by using numerical simulations. Fundamental physical correlations between the thermal, mechanical and electromagnetic fields are discussed. They occur due to the nonhomogeneous distribution of pump light inside the crystal. This photoelastic effect dominates the
eigenpolarization states of the resonator. The dissertation focuses on these eigenpolarization states.
In one application a resonator contains an Nd:YAG-crystal and Brewsterplates. There, the eigenpolarization states, the output power, the beam quality, and the polarization purity depending on the
crystal cut and its rotation are investigated. As a second example an output beam with a desired circularly polarization state is produced. The corresponding resonator with an Nd:YAG-crystal inside
uses no additional optical elements. The influence of the crystal cut to the stability ranges, output
power and beam quality are investigated.
Chapter 2 deals with the physical background of the mechanics and optics, which are used in this
dissertation. An overview of different solid state laser materials and their classifications in different
crystal classes is given. The modeling of the mechanical stiffness behavior of the crystal in anisotropic and isotropic material models is shown. Furthermore, as another physical effect, the coupling
between the mechanical and optical fields inside the crystal as well as the applicable mathematical
approach is described.
Chapter 3 considers the eigenpolarization states in solid state laser resonators with Nd:YAG-crystals
based on thermally induced birefringence. Eigenpolarization states of the resonator and their calculation with the Jones formalism are explained. The eigenmodes of the electromagnetic field are
mentioned briefly. In order to calculate the output power and the beam quality of a resonator, the
dynamic multimode analysis is shortly introduced. The parabolic fit of the indices of refraction, the
ABCD-matrix method, and the polarization depending index of refraction are described so that the
eigenpolarization behavior of solid state laser resonators can be carried out.
In chapter 4 an improvement of beam quality and output power using polarization filters inside a
resonator with an Nd:YAG crystal is explored. After the presentation of the numerical model, the
temperature and mechanical stress distribution, which occur inside the crystal and are caused by the
absorbing pump, light are shown. Subsequently, the birefringence pattern is presented. The resulting
eigenpolarization states of the resonator are calculated with and without Brewsterplates using Jones
formalism. Finally the achieved output power, beam quality, and polarization purity are compared
depending on the crystal cut direction. In case of an [100]-cut crystal this would be the rotation
around its own longitudinal axis of 0◦ and 90◦ , while for an [110]-cut crystal it would be a rotation
of 0◦ , 45◦ and 90◦ . In case of an [111]-cut crystal no rotation is considered.
One example to generate a desired polarization state is the use of different stability states due to
the photoelastic effect inside the resonator. This is investigated in chapter 5. For this purpose, the
temperature and stress distribution inside each crystal of the corresponding model are computed.
Additionally, the distribution of the indices of refraction and of the birefringence is calculated depending on the crystal cut direction. The variation of the crystal cut direction and its rotation is
equivalent to the example in the prior chapter. The thereby occurring eigenmode profiles are shown.
The length of the resonator is varied. Owing to the different shapes of the birefringence pattern, different ranges with only one specific polarization state exist. These eigenpolarisation states are either
radial or azimuthal. The ranges are calculated quantitatively depending on the crystal cut direction
and its rotation. The beam radii of the first order eigenmode, the output power, and beam quality are
3
determined and compared in these ranges.
In chapter 6 the findings of this dissertation are outlined. Moreover some limitations of this work and
a possible outlook are presented.
In summary it can be stated that when the presented numerical methods are used, an exact analysis of
the eigenpolarization states due to the stress induced birefringence in solid state laser resonators can
be performed. The use of methods based on analytical formulae, as done in the past, either limited
these analyses or made them impossible. Laser resonators with certain desired polarization states can
be effectively simulated and developed through the use of the numerical methods presented in this
paper.
4
5
0.3 Symbolverzeichnis
Symbolverzeichnis
Symbol
ai j
A
Bi j
c
Ci jkl
C
di jk
d
Di
E
Ei
fi
g
G
Hi
ji j
Ji j
k
L
L
n
pi
pi jkl
q̇i
qi jk
qi jkl
r
r
r
ri jk
Ri jkl
R
R
Si jkl
S
t
t
T
Ti j
u
(x1 , x2 , x3 )
6
Einheit
m2
m/s
N/m2
J/(kgK)
C/N
m
C/m2
N/m2
V /m
N
N/m2
A/m
1/m
m
C/m2 K
W
m/A
m2 /A2
m
m/V
m2 /V 2
m
m2 /N
J/K
s
K
m
m
Beschreibung
Transformationsmatrix
Fläche
Tensor der dielektrischen Impermeabilität
Lichtgeschwindigkeit im Vakuum
Mechanischer Steifigkeitstensor
Spezische Wärmekapazität
Piezoelektrischer Tensor
Dicke
Dielektrische Verschiebung
Elastizitätsmodul
elektrischer Feldstärkevektor
Kräftevektor
Stabilitätsfaktor
Schubmodul
Magnetischer Feldstärkevektor
Elemente der Jonesmatrix
Jonesmatrix
Wellenzahl
Länge
Resonatorverluste
Brechungsindex
Pyroelektrischer Tensor
Photoelastischer Tensor
Wärmestrom
Tensor zum linearen magnetooptischen Effekt
Tensor zum quadratischen magnetooptischen Effekt
Resonatorverlustgrad
Reflexionsgrad
Radius
Tensor zum linearen elektrooptischen Effekt
Tensor zum quadratischen elektrooptischen Effekt
Resonatorverluste
Radius
Mechanischer Nachgiebigkeitstensor
Entropie
Zeit
Transmissionsfaktor
Temperatur
Transformationstensor
Mechanische Verschiebung
Kartesisches Koordinatensystem
Symbol
αi j
αdevia
α
δ
δ
δi j
εi jk
εi j
ε0
γ
κi j
κi j
λ
λ
µ0
µ
ν
ν
ω
φ
Φ
πi jkl
ψ
Ψ
ϕ
σi j
τ
Einheit
m
As/(V m)
As/(V m)
W /(mK)
m
N/m2
N/A2
N/m2
m/s
1/s
m2 /N
N/m2
s
Beschreibung
Wärmeausdehnungstensor
Ablenkungswinkel
Drehwinkel
Optische Pfaddifferenz
Phase des elektrischen Feldes
Kronecker-Delta
Rotationstensor
Dehnungstensor
Elektrische Feldkonstante
Mechanische Gleitung
Permittivitätstensor
Wärmeleittensor
Wellenlänge
Lamékonstante
Magnetische Feldkonstante
Lamékonstante
Querkontraktionszahl
Lichtgeschwindigkeit
Kreisfrequenz
Rotationswinkel
Phasendifferenz zwischen elektrischen Feldern
Piezooptischer Tensor
Winkel der Polarkoordinaten
Rotationswinkel des Laserkristalls
Winkel der Polarisation
Spannungstensor
Resonatorlebenszeit
7
8
Inhaltsverzeichnis
0.1
0.2
0.3
Kurzzusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Abstract . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Symbolverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1 Einleitung
2 Theoretische Grundlagen von Mechanik und Optik der Kristalle
2.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Überblick über Lasermaterialien . . . . . . . . . . . . . . . . . .
2.3 Kristallsymmetrien und -klassen . . . . . . . . . . . . . . . . . .
2.4 Überblick über physikalische Effekte im Kristall . . . . . . . . . .
2.4.1 Transformationen der physikalischen Eigenschaften . . .
2.4.2 Kopplung ausgewählter physikalische Effekte im Kristall .
2.4.3 Gleichungen der thermomechanischen Kopplung . . . . .
2.4.4 Optomechanische Kopplung - der photoelastische Effekt .
1
3
6
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Eigenpolarisationszustände und deren Auswirkungen in Festkörperlasern
3.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2 Polarisation und Jonesformalismus . . . . . . . . . . . . . . . . . . . . . . . .
3.3 Eigenmoden eines Resonator . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4 Dynamische Multimode Analyse mit Polarisationsverlusten . . . . . . . . . . .
3.5 Stabilität von Laserresonatoren . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.1 Parabolischer Fit . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.5.2 ABCD-Matrixmethode und allgemeine Stabilität von Laserresonatoren
3.5.3 Polarisationsabhängige Stabilität von Laserresonatoren . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
. 3
. 3
. 4
. 5
. 5
. 6
. 7
. 11
.
.
.
.
.
.
.
.
17
17
17
21
21
22
22
24
26
.
.
.
.
.
.
.
.
4 Verbesserung der Strahlqualität und Ausgangsleistung durch Verwendung eines
Polarisationsfilters
4.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Numerisches Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Räumliche Verteilung der Temperatur, der mechanischen Dehnungen und Spannungen
4.4 Räumliche Verteilung der Doppelbrechung . . . . . . . . . . . . . . . . . . . . . . .
4.5 Eigenpolarisationszustände im Resonator ohne Brewsterplatte . . . . . . . . . . . .
4.6 Eigenpolarisationszustände im Resonator mit Brewsterplatte . . . . . . . . . . . . .
4.7 Vergleich von Ausgangsleistung, Strahlqualität und Polarisationsreinheit . . . . . . .
4.8 Zusammenfassung und Schlussfolgerung . . . . . . . . . . . . . . . . . . . . . . . .
27
27
28
30
33
33
35
40
43
5 Erzeugung eines bestimmten Polarisationszustandes mittels Stabilität des Resonators
45
i
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Numerisches Modell . . . . . . . . . . . . . . . . . . . . . . .
Temperaturverlauf und mechanische Spannungen . . . . . . . .
Räumlich Verteilung der Brechungsindizes . . . . . . . . . . . .
Doppelbrechungsmuster . . . . . . . . . . . . . . . . . . . . .
Laguerre-Mode-Profile . . . . . . . . . . . . . . . . . . . . . .
Länge der Stabilitätsbereiche . . . . . . . . . . . . . . . . . . .
Strahlradien des Modes 1. Ordnung der erzeugten Polarisationen
Ausgangsleistungen der erzeugten Polarisationen . . . . . . . .
Strahlqualität der erzeugten Polarisationen . . . . . . . . . . . .
Zusammenfassung und Schlussfolgerung . . . . . . . . . . . . .
6 Zusammenfassung und
6.1 Zusammenfassung
6.2 Einschränkungen .
6.3 Ausblick . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
45
46
48
50
52
54
55
58
61
64
67
Ausblick
69
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Abbildungsverzeichnis
73
Literaturverzeichnis
77
ii
1 Einleitung
Seit der erste Rubinlaser in den 1960er Jahren aufkam, ist er zum bedeutenden Teil der modernen
Kultur geworden. Eine Vielzahl von Sciencefictionfilmen und Romanen kommt nicht ohne Laser
aus. Aber schon in der Gegenwart kommen wir keinen Tag ohne Laser aus: Wir benutzen ihn in
CD/DVD-Playern, Laserdruckern, Barcodelesern, Medizin, Produktion usw. Viele Anwendungen
benötigen ein bestimmtes Verhalten vom Laserstrahl, wie eine bestimmte Polarisation, Strahlqualität, Strahldivergenz, etc. Viele verschiedene Arten von Lasern sind heute in Gebrauch, wie z.B.
Gaslaser, Faserlaser, Halbleiterlaser oder Festkörperlaser. Alle Laserarten arbeiten nach dem gleichen Prinzip: Pumplicht oder elektrische Felder oder chemische Reaktionen bewegen Elektronen des
Verstärkermediums von einem Grundlevel auf ein höheres Level. Über verschiedene Zwischenstufen bewegen sich die Elektronen wieder zurück auf das Grundniveau. Dabei geben sie Photonen mit
einer gewissen Frequenz ab. Gezielt entstehen viele solcher Photonen im Laserresonator mit Hilfe
der stimulierten Emission. Ein Teil dieser Photonen verlässt den Resonator als kohärenter Lichtstrahl
mit möglichst einer einzelnen Frequenz. Aber es wird nicht die gesamte Pumpenergie in Laserlicht
umgewandelt. Es treten Verluste auf, welche das Verstärkermedium erwärmen. Dabei kann sich in
Gaslasern die Wärme homogen verteilen. Aber in Festkörperlaserkristallen ist, aufgrund des inhomogen verteilten Pumplichts, dem festen Verbleiben der Atome an ihrem Platz und der Möglichkeit
nur die Kristalloberfläche zu kühlen, die Wärmeverteilung sehr ungleichmäßig. Es treten demnach
Temperaturgradienten im Kristall auf, welche zu inhomogen verteilten mechanischen Verschiebungen in diesem führen. Dies resultiert dann in mechanischen Dehnungen und Spannungen im Kristall.
Alle Kristallarten haben die Eigenschaft ihren Brechungsindex bei reiner Temperaturänderung zu
ändern, wobei dieser aber für Licht beliebiger Polarisation konstant bleibt. Durch die inhomogene
Temperaturverteilung ist der Brechungsindex ebenfalls inhomogen über den Kristallquerschnitt verteilt. Eine thermische Linse entsteht, welche die Lichtstrahlen inner- und außerhalb des Resonators
ungewollt ablenken kann. Des Weiteren ändert sich der Brechungsindex aufgrund der mechanischen
Spannungen auch noch polarisationsabhängig. Dies wird der photoelastische Effekt genannt. Es tritt
eine spannungsinduzierte Doppelbrechung auf. Eine Lichtwelle einer Polarisation erfährt einen anderen Brechungsindex als eine einer anderen Polarisation. Damit kann eine angestrebte Polarisation
des Ausgangsstrahls ungewollt verfälscht werden. Eine Möglichkeit dies zu kompensieren ist das
Einbauen von Brewsterplatten in den Resonator, um einen linear polarisierten Ausgangsstrahl zu
erreichen. Die Brewsterplatten dämpfen polarisationsabhängig einen Teil der elektromagnetischen
Welle innerhalb des Resonators. Aber auch das ideal linear polarisierte Ausgangslicht wird wegen
des photoelastischen Effekts nicht ganz erreicht. Inwiefern die Ausgangsleistung, die Ausgangspolarisation und die Strahlqualität davon beeinflusst werden und welche Rolle dabei der Schnitt des
Laserkristalls und seine Rotation um seine Längsachse innerhalb des Resonators spielt, ist ein Gegenstand der vorliegenden Arbeit.
Aber die spannungsinduzierte Doppelbrechung des Laserkristalls kann auch benutzt werden, um
einen Laserresonator zu bauen, der ohne zusätzliche optische Elemente ein zirkular polarisiertes
Licht aussendet. Dabei wird ausgenutzt, dass das Licht unterschiedlicher Polarisationen unterschied-
1
liche Brechungsindizes erfährt. Bei einer bestimmten Resonatorgeometrie wird z.B. nur Licht einer
radialen Polarisation verstärkt, während der azimutale Polarisationszustand nicht anschwingen kann.
Bei einer anderen Resonatorkonfiguration kann es aber auch umgedreht sein, das heißt, dass nur
azimutal polarisiertes Licht verstärkt wird. An einem solchen Beispiel werden in dieser Arbeit die
Ausgangsparameter Strahlqualität und Ausgangsleistung in Abhängigkeit vom Kristallschnitt und
dessen Drehung untersucht, indem die Länge des Resonators bei gleich bleibenden anderen Parametern variiert wird.
Änliche Untersuchungen wurden bisher meist mit analytischen Methoden durchgeführt. Diese Arbeit benutzt dagegen eine dreidimensionale Finite-Element-Methode zur Berechnung der Strukturmechanik und einen zweidimensionalen Jonesformalismus zur Bestimmung der Eigenpolarisationszustände der elektromagnetischen Welle im Resonator. Mit diesen Simulationsmethoden sind sehr
genaue Ergebnisse erzielbar, welche kostspielige und aufwendige Versuche bei der Laserentwicklung reduzieren können.
2
2 Theoretische Grundlagen von Mechanik
und Optik der Kristalle
2.1 Einleitung
Für die Untersuchung von Kristallverhalten in Festkörperlaserresonatoren ist es notwendig, die Arten von Kristallen zu kennen, d.h. sie in Abhängigkeit von inneren Symmetrien einordnen zu können.
Unterschiedliche innere Symmetrieeigenschaften bedingen unterschiedliche physikalische Eigenschaften. Ein Überblick über diese Eigenschaften und dessen richtungsabhängige Handhabung in
Abhängigkeit von den Kristallschnittrichtungen ist hier dargestellt. Dabei wird insbesondere auf die
thermomechanische und optomechanische Kopplung eingegangen.
2.2 Überblick über Lasermaterialien
Das Verstärkermedium eines Festkörperlaser besteht entweder aus einer Keramik oder einem Glas
oder einem Kristall, siehe [1]. Laserkristalle bestehen aus einem einzigen Einkristall und damit aus
einer gleichmäßigen Gitterstruktur mit einer bestimmten Orientierung und sind makroskopisch mechanisch anisotrop, siehe [2]. Makroskopisch meint hier das Verhalten des ganzen Körpers. Mikroskopisch meint das Verhalten der einzelnen Körner, das heißt den räumlichen Teilbereichen des
Kristalls. Keramiken bestehen aus vielen verschiedenen orientierten Einzelkristallen, den Körnern,
und sind damit mikroskopisch anisotrop aber makroskopisch isotrop. Gläser sind dagegen komplett
amorph und damit sowohl mikroskopisch als auch makroskopisch isotrop. Die möglichen Dopingkonzentrationen der Dotierungsmaterialien, wie z.B. Nd3 + -Ionen, sind in Kristallen geringer als in
Gläsern oder Keramiken. Glasverstärker können in größeren Dimensionen hergestellt werden als kristalline Verstärker. Die Laserschwelle ist höher und die thermische Leitfähigkeit ist geringer als bei
Kristallen. Durch letzteres ist in Glaslasern die thermisch induzierte Doppelbrechung auch größer
und der Verstärker ist mechanisch empfindlicher bei hohen Pumpleistungen, siehe [1]. In Gläsern
sind die Fluoreszenzlinienbandweiten größer, die optische Qualität und die Dopinghomoginität sind
besser und die Absorptionslinien sind weiter. Keramik hat gegenüber Glas und Kristallen den Vorteil,
dass sie preisgüstiger sind und eine höhere thermische Leitfähigkeit besitzen. Allerdings sind auch
die Streuverluste höher. In einer Keramik sind die Einzelkristallkörner statistisch orientiert, wodurch
die thermisch induzierte Doppelbrechung einen Durchschnittswert annimmt. Dieser Durchschnittswert entspricht in etwa der Doppelbrechung eines in [111]-Richtung geschnittenen Kristalls und ist
annähernd rotationssymmetrisch über dem Querschnitt verteilt, siehe [3] und [4]. In der vorliegenden
Arbeit wird sich mit den Kristallen als Verstärkermedium beschäftigt.
3
2.3 Kristallsymmetrien und -klassen
Kristalle treten in der Natur in großer Vielfalt auf, siehe [5]. Menschen züchten seit etwa ca. 2700 v.
u. Z. Salzkristalle, [6]. Zu den künstlichen Kristallen zählt auch der nicht in der Natur vorkommende Yttrium-Aluminium-Granat-Kristall (kurz: YAG, chemische Formel: Y3 Al5 O12 ). Dieser wird seit
etwa Mitte des 20. Jahrhunderts hergestellt und hauptsächlich in LEDs und Festkörperlasern verwendet.
Gemeinsame Eigenschaft aller Kristalle ist die regelmäßige Gitterstruktur, wodurch sie eine innere Symmetrie aufweisen. Die verschiedenen Kristallformen werden dabei nach ihren verschiedenen
Gitterstrukturen und damit ihren verschiedenen möglichen Symmetrieoperationen unterschieden, die
an ihrer Einheitszelle durchgeführt werden können, siehe [7]. Symmetrieelemente sind dabei die
Drehachsen und die Drehinversionsachsen, welche auch die Spiegelebenen und das Inversionszentrum enthalten. Durch die entsprechenden Symmetrieoperationen lassen sich die Symmetrieelemente
mit sich selbst zur Deckung bringen. Da die Einheitszellen von verschiedenen Kristallen verschiedene Kantenlängen und Winkel der Kanten zueinander haben, sind jeweils nur bestimmte Symmetrieoperationen möglich. Durch diese werden sieben Kristallsysteme definiert, welche wiederum in 32
Kristallklassen (Punktgruppen) untergliedert werden:
Kristallsysteme
• triklines Kristallsystem,
• monoklines Kristallsystem,
• orthorhombisches (orthotropes oder rhomisches) Kristallsystem,
• tetragonales Kristallsystem,
• trigonales Kristallsystem,
• transversal-isotropes (hexagonales) Kristallsystem und
• kubisches Kristallsystem.
Dabei gehören z.B. zum kubischen Kristallsystem die Kristallklassen 23, m3, 432, 43m und m3m.
Bezüglich der übrigen Kristallklassen sei z.B. auf folgende Fachliteratur verwiesen: [7, 8, 9]. Weiterhin werden alle Kristalle in 230 verschiedene kristallographische Raumgruppen eingeordnet. Als in
den Festkörperlaserresonatoren häufig verwendete Wirtskristalle seien hier YAG (Y3 Al5 O12 , kubisches Kristallsystem, Kristallklasse m3m), Vanadat (YV04 , tetragonal, 4/mmm) und Rubin (Al2 O3 ,
trigonal, 32/m) erwähnt, siehe auch [10]. Die verschiedenen Symmetrien der Kristallklassen führen
zu unterschiedlichen physikalischen Eigenschaften. Nach dem Neumannschen Prinzip muss die Symmetrie jeder physikalischen Eigenschaft die Symmetrieelemente der Punktgruppe des Kristalls beinhalten, siehe [8]. Dies hat zur Folge, dass einige Kristallklassen bestimmte physikalische Eigenschaften aufweisen, die andere wiederum nicht besitzen. Dies wird in Kapitel 2.4.2 näher erläutert.
4
2.4 Überblick über physikalische Effekte im
Kristall
Die hier verwendeten physikalischen Materialeigenschaften und Zustandsgrößen werden geometrisch mit Tensoren unterschiedlicher Stufe beschrieben, siehe z.B. [7, 8, 9]. Als Tensor 0. Stufe
wird z.B. die Massendichte, als Tensor 1. Stufe z.B. die Pyroelektrizität, als Tensor 2. Stufe z.B. die
thermische Leitfähigkeit, als Tensor 3. Stufe z.B. die Piezoelektrizität und als Tensor 4. Stufe z.B.
die Elastizität dargestellt.
2.4.1 Transformationen der physikalischen Eigenschaften
Es wird in polare und axiale Tensoren bzw. in polare und axiale Tensoreigenschaften unterschieden.
Im Gegensatz zu axialen Tensoren ändern sich die Vorzeichen von polaren Tensoren nicht, wenn
sich die Händigkeit (Rechts- und Linkshändigkeit) ändert, siehe [9]. In dieser Arbeit werden nur
physikalische Effekte betrachtet, die durch polare Tensoren beschrieben werden. Deren allgemeines
Transformationensgesetz für die Umrechnungen eines beliebigen Tensors T in ein anderes Koordinatensystem T 0 lautet:
Ti0jk... = ail a jm akn ...Tlmn... .
(2.1)
Dabei sind ai j die Transformationensmatrizen und es wird zur Summation der Indizes die Einsteinsche Summenkonvention verwendet. Für die Drehung um einen Winkel α um die x1 -Achse a1 , um
die x2 -Achse a2 und um die x3 -Achse a3 lauten diese Matrizen jeweils:

1
0
0


cos(α)
0 sin(α)





0
1
0
α1 =  0 cos(α) − sin(α)  , α2 = 
 und
0 sin(α) cos(α)
− sin(α) 0 cos(α)


cos(α) − sin(α) 0


α3 =  sin(α) cos(α) 0  .
0
0
1
(2.2)
Der Wert eines Tensors 0. Stufe ist invariant gegenüber Koordinatentransformationen.
Koordinatentransformationen werden z.B. angewendet, um die in einem Referenzkoordinatensystem
vorliegenden Materialeigenschaften in das aktuelle, von der Schnittrichtung abhängige Koordinatensystem des Laserkristalls zu transformieren. Um die Transformationensmatrix ai j zu dem zugehörigen Kristallschnitt zu bestimmen, wird in dieser Arbeit das Gram-Schmidt Orthogonalisierungsverfahren angewendet, siehe [11]. Innerhalb des Resonators kann der Kristall noch beliebig gedreht
werden, wodurch eine Koordinatentransformation um die x3 -Achse mit α3 , siehe Gleichung (2.2),
verwendet wird. Für das Beispiel des kubischen Kristallsystems ist in Abbildung 2.1(a) die Kristallorientierung in der [100]-Schnittrichtung und in Abbildung 2.1(b) in der [111]-Schnittrichtung
dargestellt. Diese Angaben der Kristallschnittrichtungen beziehen sich auf die Miller’schen Indizes,
welche z.B. in [5] beschrieben sind.
5
(a)
(b)
Abbildung 2.1: Koordinatensystem im kubischen Gitter (a) in [100]-Schnittrichtung und (b) in [111]Schnittrichtung.
2.4.2 Kopplung ausgewählter physikalische Effekte im
Kristall
In Bild 2.2 ist das Heckmann Diagramm zu den physikalische Kopplungen der elektrischen, mechanischen und themischen Felder dargestellt, siehe auch [8, 9]. Darin sind Korrelationen zwischen
der Pyroelektrizität, Permittivität, Piezoelektrizität, Elastizität, spezifischer Wärme und thermischer
Ausdehnung zu sehen. Als Feldgrößen treten dabei das elektrische Feld Ei , die dielektrische Verschiebung Di , die mechanischen Dehnungen εi j und Spannungen σi j , sowie die Entropy je Einheitsvolumen S und die Temperatur T auf. Eine mögliche formelmäßige Handhabung dieser Kopplungen
lautet:
T
E
εi j = SiE,T
jkl σkl + dki j Ek + αi j ∆T ,
(2.3)
Di = diTjk σ jk + κiσj ,T E j + pσi ∆T und
∆S = αiEj σi j + pσi Ei + Cσ ,E /T ∆T .
(2.4)
(2.5)
Darin ist Si jkl der mechanische Nachgiebigkeitstensor, di jk der piezoelektrische Tensor, αi j der Tensor der thermischen Ausdehnung, κi j der Permittivitätstensor, pi die pyroelektrischen Koeffizienten
und C die Wärmekapazität je Einheitsvolumen. Auf weitergehende Beschreibungen, wie z.B. direkte
und indirekte Effekte oder adiabate und isotherme Prozesse, sei hier aus Übersichtlichkeitsgründen
verzichtet und auf die bereits zitierte Fachliteratur verwiesen.
Nach dem Neumannschen Prinzip verbietet ein Inversionszentrum in der Kristallstruktur ungeradstufige physikalische Eigenschaften wie Pyroelektrizität und Piezoelektrizität, siehe [8]. Da Kristalle
der Kristallklassen m3, 432 und m3m des kubischen Kristallsystems ein solches besitzen, treten die
eben genannten physikalischen Effekte dort nicht auf; alle Elemente von di jk sind in diesem Kristallsystem null und eine Kopplung zwischen mechanischen und elektrischen Feldern ist nicht existent.
Deswegen treten in der Kristallklasse m3m auch keine pyromagnetischen, magnetoelektrischen oder
piezomagnetischen Kopplungen auf.
Des Weiteren beträgt die Anzahl der unabhängigen Materialkonstanten im Fall von Beschreibbarkeit
mit Tensoren zweiter Stufe eins. Das heißt z.B., dass es im YAG-Kristall nur einen Materialwerte für
6
Abbildung 2.2: Übersicht über physikalische Effekte im Kristall durch Heckmann Diagramm, angelehnt an [8, 9].
die thermische Ausdehnung, der Wärmeleitung und der elektrischen Leitfähigkeit gibt, siehe [8] und
[9].
2.4.3 Gleichungen der thermomechanischen Kopplung
In diesem Abschnitt werden die Grundgleichungen der Elastizitätstheorie im statischen Fall dargestellt. Dabei wird das linear-elastische Steifigkeitsverhalten (Hooksches Gesetz) für ein isotropes und ein orthotropes Materialmodell angeben. Es werden in zwei Arten von thermischen und
mechanischen Randbedingungenen unterschieden. Damit können aus vorgegebenen mechanischen
und thermischen Lasten und Randbedingungen die mechanischen Verschiebungen, Dehnungen und
Spannungen im Laserkristall berechnet werden. Die Berechnung der thermischen Felder im Kristall
ist in [12] beschrieben.
Grundgleichungen der Elastizitätstheorie
In diesem Abschnitt wird auf die Gleichung (2.3) ohne den piezoelektrischen Effekt eingegangen,
da dieser im YAG-Kristall nicht auftritt. Das heißt, es wird die Kopplung zwischen dem mechanischen und dem thermischen Feld beschrieben. Diese Grundgleichungen sind in vielen Büchern wie
7
[8] und [13] dargestellt. Aufgrund der hohen Sprödigkeit von Laserkristallen wird nur der linear elastische Fall betrachtet. Des Weiteren wird von quasi-statischem Verhalten ausgegangen. Folgende
Grundgleichungen der Elastizitätstheorie bestimmen die mechanischen Feldgrößen Spannungen σi j ,
Dehnungen εi j und Verschiebungen ui :
σkl,k + fl = 0 and σkl = σlk
1
εkl = (uk,l + ul,k ) + αkl ∆T
2
σi j = Ci jkl (εkl − αi j ∆T )
εi j = Si jkl σkl + αi j ∆T
Kräftegleichgewicht,
(2.6)
Kinematische Gleichung,
(2.7)
Hooksches Gesetz,
(2.8)
Hooksches Gesetz,
(2.9)
wobei fl Körperkräfte, Ci jkl die mechanische Steifigkeit, Si jkl die mechanische Nachgiebigkeit und
αi j der Wärmeausdehnungstensor ist.
Wie bereits im Abschnitt 2.1 beschrieben, sind Kristalle von anisotroper Natur. In gewissen Fällen
ist bei dem mechanischen Werkstoffverhalten jedoch eine vereinfachte Modellierung als annähernd
isotroper Werkstoff nützlich, wenn der Grad der Anisotropie schwach ist. Beim YAG-Kristall ist das
z.B. der Fall, siehe [14] und Abschnitt 4.3. In folgenden Abschnitten wird zunächst dieses isotrope
und anschließend das anisotrope Werkstoffstoffverhalten beschrieben. Für die Darstellung der mechanischen Gleichungen wird hier die Voigtsche Konvention verwendet, d.h. die Tensoren vierter
Stufe werden zu Tensoren zweiter Stufe und die Tensoren von ursprünglich zweiter Stufer zu Tensoren erster Stufe verjüngt, siehe [15]. Die Gleichungen (2.8) und (2.9) des Hookschen Gesetzes lauten
damit:
σi = Ci j (ε j − α j ∆T ) und
(2.10)
εi = Si j σ j + αi ∆T .
(2.11)
Aus Symmetriegründen, siehe u.a. [8, 9], sind sowohl Ci j als auch Si j symmetrisch, d.h. es gibt maximal 21 verschiedene Materialparameter. Dies ist im triklinen Kristallsystem der Fall.
Isotrope Materialbeschreibung
Bei diesem Materialverhalten sind sämtliche Materialparameter richtungsunabhängig, d.h. die Reaktion des Körpers auf äußere und innere Lasten ist immer gleich, unabhängig, wie dieser orientiert
ist. Bei einem isotropen Material gibt es nur noch zwei mechanische Materialparameter: Den Elastizitätsmodul E und die Querkontraktionszahl ν. Diese bilden die Lamékonstanten:
λ
=
µ =
8
νE
und
(1 + ν) (1 − 2ν)
E
= G,
2 (1 + ν)
(2.12)
(2.13)
wobei G = µ auch als Schubmodul bezeichnet wird.
siehe Gleichung (2.10), lautet in Voigtscher Notation:
  λ + 2µ

λ
λ
0
σ1 = σ11
 σ =σ  
λ
λ + 2µ
λ
0

22 
 2
 

λ
λ
λ + 2µ 0
 σ3 = σ33  
=


 σ =σ  
0
0
0
µ
23 
 4
 

0
0
0
0
 σ5 = σ13  

σ6 = σ12
0
0
0
0
Das Hooksche Gesetz für isotropes Material,
0
0
0
0
0
0
0
0
µ
0
0
µ
 
 
 
 
 
 
 · 
 
 
 

ε1 = ε11



ε2 = ε22 






ε3 = ε33
 − α∆T  . (2.14)

ε4 = 2ε23 





ε5 = 2ε13 
ε6 = 2ε12
Gleichung (2.11) lautet analog:



1 −ν −ν
0
0
0
ε1 = ε11

 ε =ε 
0
0
0
 −ν 1 −ν
22 
 2



−ν −ν 1
0
0
0
 ε3 = ε33  1 

= 

 ε = 2ε  E  0
0
0 2 (1 + ν)
0
0
23 
 4



 0
0
0
0
2 (1 + ν)
0
 ε5 = 2ε13 

0
0
0
0
0
2 (1 + ν)
ε6 = 2ε12
 
 
 
 
 
 
·
 
 
 

σ1



σ2 






σ3
 + α∆T 

σ4 





σ5 
1

1 


1 
.
0 


0 
0
(2.15)
Man beachte, dass aufgrund der Voigtschen Notation, d.h. der Verjüngung des vierstufigen Tensors
Ci jkl auf den zweistufigen Tensor Ci j , bei der Berechnung von σi bei den Scherdehnungen ε23 , ε13
und ε12 ein Faktor 1/2 eingefügt werden muss. Damit ergibt sich beispielsweise der Zusammenhang
ε4 = 2ε23 = γ23 ,
(2.16)
σ6
wobei γi j für i 6= j auch als technische Gleitung bezeichnet wird.
Anisotrope Materialbeschreibung
Bei dem anisotropen Materialverhalten sind die Reaktionen des Körpers auf äußere und innere Lasten
von dessen Orientierung abhängig. Unter der Annahme, dass hochanisotrope Kristalle als Festkörperlaserverstärkermedien ungeeignet sind, da sie eine hohe natürliche Doppelbrechung aufweisen und
eine symmetrische Kühlung aufgrund der anisotropen Wärmeleitfähigkeit nur schwer möglich ist,
werden in dieser Arbeit die triklinen und monoklinen Kristallsysteme nicht berücksichtigt. Für das
orthotrope Kristallsystem lautet das Hooksche Gesetz, siehe [16]:
 
 
 

  1−ν23 ν32 E
ν12 +ν32 ν13
E2 ν13 +νΨ12 ν23 E3 0
0
0
1
ε1
σ1
α1
Ψ
Ψ
 
ν21 +ν31 ν23
 
 
 σ  
E1 1−νΨ13 ν31 E2 ν23 +νΨ21 ν13 E3 0
0
0 
 ε2   α2  
 2  
Ψ


 





  ν31 +ν21 ν32
 ε3   α3  
 σ3  
E1 ν32 +νΨ12 ν31 E2 1−νΨ12 ν21 E3
0
0
0 

Ψ

 




=
 
 −  α  ∆T  .
 σ  

0
0
0
G
0
0
ε
23
 4   4  
 4  

 

 




 σ5  
0
0
0
0
G
0
13
  ε5   α5  

0
0
0
0
0 G12
ε6
α6
σ6
(2.17)
9
Mit
Ψ = 1 − ν12 ν21 − ν23 ν32 − ν31 ν13 − 2ν21 ν32 ν13 ,
ν21 ν12
ν32 ν23 ν31 ν13
=
,
=
und
=
.
E3
E2 E3
E1
E1
E1
Gleichung (2.11) lautet im orthotropen Kristallsystem analog:
 

  1
− νE212 − νE313
0
0
0
ε1 = ε11
E1

ν
1
 ε =ε  
− νE323
0
0
0  
 − E121
22 
E2
 2
 



ν23
ν13
1
 
−
0
0
0
−
 ε3 = ε33  
E
E
E
 

1
2
3


·
1
 ε = 2ε  = 
0
0
0
0  
 0
23 
 4
G
23
 

 
1
 
0
0
0
0
0
 ε5 = 2ε13  
 

G13
1
0
0
0
0
0 G12
ε6 = 2ε12
σ1

(2.18)
(2.19)

α1


σ2 





σ3 
 + α∆T 


σ4 




σ5 
α2 


α3 
.
α4 


α5 
σ6
α6
(2.20)
In diesem orthotropen Kristallsystem sind neun unabhängige mechanische Materialparameter vorhanden: E1 , E2 , E3 , ν23 , ν13 , ν12 , G23 , G13 und G12 . In den übrigen Kristallsystemen (tetragonal,
trigonal, transversal-isotrop und kubisch) ist die Anzahl der unabhängigen Materialparameter kleiner als neun, siehe Tabelle 2.1 und [9]. Man beachte auch, dass bei der Verjüngung des Tensors der
thermischen Ausdehnung, analog zu den Dehnungen, ein Faktor von 1/2 hinzugefügt werden muss,
so dass α4 = 2α23 , α5 = 2α13 und α6 = 2α12 gilt.
Kristallsystem
Triklin
Monoklin
Orthorhombisch
Tetragonal
Trigonal
Hexagonal
Kubisch
(Isotrop)
Ci j
21
13
9
6,7
7
5
3
2
αi j
6
4
3
2
2
2
1
1
pi j
36
20
12
7,10
8,13
6,8
3,4
-
Tabelle 2.1: Anzahl unabhängiger Materialkonstanten der mechanischen Steifigkeit Ci j , der thermischen Ausdehnung αi j und der photoelastischen Kopplung pi j (siehe Abschnitt 2.4.4) in
Abhängigkeit von den verschiedenen Kristallsystemen. Wenn ein Eintrag mehr als eine
Zahl aufweist, ist die Anzahl zusätzlich von der Kristallklasse abhängig, siehe auch [9].
10
Mechanische und thermische Randbedingungen
In dieser Arbeit werden zwei Arten von Randbedingungen verwendet: die Dirichlet- und die NeumannRandbedingungen:
Dirichlet Randbedingungen: Die Verschiebungen ui bzw. Temperaturen T sind als Funktionen
gmech (x1 , x2 , x3 ) bzw. gtherm (x1 , x2 , x3 ) an den Rändern des Gebietes Ω gegeben:
ui = gmech (x1 , x2 , x3 ) auf Ω und
(2.21)
= gtherm (x1 , x2 , x3 ) auf Ω.
(2.22)
T
Neumann Randbedingungen: Im mechanischen Fall sind die Kräfte fi (x1 , x2 , x3 ) in Normalenrichtung n j auf den Randgebieten als Funktion und im thermischen Fall als Wärmestrom q̇i (x1 , x2 , x3 )
gegeben:
σi, j n j = fi (x1 , x2 , x3 ) auf Ω und
∂T
−ki j
= q̇i (x1 , x2 , x3 ) auf Ω,
∂xj
(2.23)
(2.24)
wobei ki j der Tensor der Wärmeleitkoeffizienten ist. Ein vorgegebener Wärmestrom kann z.B. durch
die Absorption von Pumplicht im Laserkristall entstehen.
2.4.4 Optomechanische Kopplung - der photoelastische
Effekt
Zur Beschreibung des photoelastischen Effekts wird zunächst aus den Maxwellgleichungen und dem
Ansatz für elektromagnetische Wellen in einem nichtmagnetischen optisch anisotropen Material die
Indicatrix, d.h. der Tensor der unterschiedlichen Brechungsindizes hergeleitet. Durch die Kopplung
der auftretenden mechanischen Dehnungen, bzw. Spannungen mit dem photoelastischen Tensor, welcher einem Materialwert entspricht, wird diese Indicatrix berechnet. Dabei ist darauf zu achten, dass
die häufig in [100]-Schnittrichtung gemessenen Materialwerte ggf. in das Koordinatensystem der
Schnittrichtung des im Laserresonator verwendeten Kristalls transformiert werden müssen, siehe
Gleichung (2.1).
Maxwellgleichungen und elektromagnetische Wellengleichung
Grundlagen der elektromagnetischen Wellenausbreitung sind die Maxwellgleichungen. Diese lauten
in der Tensorform für ein nichtmagnetisches Material, siehe [9]:
∂ Hk
∂xj
∂ Ek
εi jk
∂xj
∂ Di
∂ xi
∂ Hi
µ0
∂ xi
εi jk
∂ Di
,
∂t
∂ Hi
= −µ0
,
∂t
=
(2.25)
(2.26)
= 0 und
(2.27)
= 0.
(2.28)
11
Dabei ist Ei die elektrische Feldkomponente und Hi die magnetische Feldkomponente der elektromagnetischen Welle. Di ist die dielektrische Verschiebung, t die Zeit, µ0 die magnetische Feldkonstante
und εi jk ist der Rotationstensor. Wenn i, j und k alle verschieden sind, dann ist εi jk = 0. Wenn i, j und
k in zyklischer Reihenfolge auftreten, ist εi jk = +1 und in antizyklischer Reihenfolge −1. Weiterhin
gilt
Di = εi j E j und
(2.29)
Ei = µ0 Hi .
(2.30)
Eine monochromatische elektromagnetische Welle kann mit der Kreisfrequenz ω, den Amplituden
E0i und H0i und dem Wellenvektor ki beschrieben werden:
Ei = E0i ei(ωt−ki xi ) und
i(ωt−ki xi )
Hi = H0i e
.
(2.31)
(2.32)
Wobei
k = (k1 , k2 , k3 ) und |k| = 2π/λ .
(2.33)
Darin ist λ die Wellenlänge der monochromatischen Welle und N ist die Wellennormale.
Die Lichtgeschwindigkeit im Vakuum c ergibt sich aus
c= √
1
,
µ0 ε0
(2.34)
wobei ε0 die elektrische Feldkonstante im Vakuum ist. Nach dem Einsetzen der Gleichungen (2.31)
und (2.32) in die Maxwellgleichungen (2.25) und (2.26) und einigen Umformungen, siehe [9], ergibt
sich in einem nichtmagnetischen Material:
N32
Ni2
N12
N22
=
+
+
= 0,
(1/ (µ0 εii ) − ν 2 ) ν12 − ν 2 ν22 − ν 2 ν32 − ν 2
wobei
ν12 =
1
1
1
, ν22 =
und ν32 =
.
µ0 ε11
µ0 ε22
µ0 ε33
(2.35)
(2.36)
Darin sind εii die Komponenten des Dielektrizitätstensors im Hauptachsensystem. In diesem Hauptachsensystem besteht zwischen den Brechungsindizes ni und den Lichtgeschwindigkeiten νi folgender Zusammenhang:
c
c
c
ν1 = , ν2 =
und ν3 = .
(2.37)
n1
n2
n3
In dem triklinen, monoklinen und orthorhombischen Kristallsystem treten nach dem Neumannschen
Prinzip im Hauptachsensystem immer drei verschiedene Brechungsindizes auf, siehe [9]. Diese Kristalle werden optisch zweiachsig genannt. In den tetragonalen, trigonalen und hexagonalen Kristallsystemen treten im unbelasteten Zustand im Hauptachsensystem zwei verschiedene Brechungsindizes no (zum ordinärer Strahl“gehörend) und ne (zum extraordinärer Strahl“gehörend) auf. Diese
”
”
werden optisch einachsig genannt. Im kubischen Kristallsystem ist n natürlich isotrop, d.h. der Brechungsindex ist in allen Richtungen gleich. Die Auswirkungen der unterschiedlichen Brechungsindizes auf z.B. den Wellenvektor und die Strahlrichtung sind in Lehrbüchern, wie z.B. [17], detailiert
beschrieben.
12
Die Indicatrix
Neben der Darstellung mit den Wellennormalen können die Brechungsindizes auch mit der optischen
Indicatrix beschrieben werden, welche in Abbildung 2.3 dargestellt ist. Gleichung (2.35) wird im
Abbildung 2.3: Indicatrix, [18]
Hauptachsensystem folgendermaßen dargestellt:
x12 x22 x32
+ +
n21 n22 n23
= 1 und
B1 x12 + B2 x22 + B3 x32 = 1.
(2.38)
(2.39)
Dabei ist dielektrische Impermeabilität Bi j im Hauptachsensystem als
B1 =
1
1
1
, B2 = 2 und B3 = 2
2
n1
n2
n3
(2.40)
definiert. Die Indicatrix ist damit im allgemeinen Fall ein Ellipsoid.
Die Differenz der Brechungsindizes zwischen der schnelleren und der langsameren Geschwindigkeit
im Hauptachsensystem in der Ebene senkrecht zur Lichtausbreitung, d.h. zwischen dem kleineren
und dem größeren Brechungsindex wird als Doppelbrechung ∆n definiert. Das heißt
∆n = nlangsam − nschnell , wobei nlangsam > nschnell .
(2.41)
Wie oben geschrieben ist der Brechungsindex in einem optisch isotropen Material in jeder Richtung
gleich, d.h. n1 = n2 = n3 = n0 . Die Indicatrix ist in diesem Fall eine Kugel. Die Phasendifferenz δ
ist im allgemeinen Fall definiert als
δ=
2π
L nlangsam − nschnell ,
λ
(2.42)
wobei λ die Wellenlänge und L die Länge des zugehörigen Elements sind, siehe z.B. [19]. Die
optische Pfaddifferenz δl , siehe u.a. [1], ist
L nlangsam − nschnell
δl =
.
(2.43)
λ
13
Der photoelastische Effekt
Eine Änderung der Indicatrix ∆Bi j kann durch den photoelastischen Effekt, durch elektrooptische
Effekte (den Pockels- und den Kerreffekt), sowie durch magnetooptische Effekte erfolgen, siehe
[9]:
∆Bi j = pi jkl εkl + ri jk Ek + Ri jkl Ek El + qi jk Hk + qi jkl Hk Hl .
(2.44)
Darin ist pi jkl der photoelastische Tensor und εi j sind die mechanischen Dehnungen. Ei und Hi
sind auftretende elektrische und magnetische Felder. ri jk ist der Tensor zum linearen elektrooptischen Effekt (Pockelseffekt), Ri jkl der Tensor zum quadratischen elektrooptischen Effekt (Kerreffekt). qi jk und qi jkl gehören zum linearen bzw. quadratischen magnetooptischen Effekt (CottonMouton-Effekt). Der Pockelseffekt und der lineare magnetooptische Effekt treten im YAG Kristall
aus Symmetriegründen der Kristallstruktur nicht auf, [9]. Der elektrooptische Effekt wird im allgemeinen beim YAG vernachlässigt, siehe [20]. Der quadratische magnetooptische Effekt ist beim
YAG-Kristall in der Literatur bisher nicht erwähnt worden. In dieser Arbeit wird nur der photoelastische Effekt betrachtet, d.h. es wird nur auf die Änderung des Brechungsindexes aufgrund mechanischer Dehnungen εi j und Spannungen σi j eingegangen. Gleichung (2.44) kann dann als
Bi j = Bi j,0 + ∆Bi j = Bi j,0 + pi jkl εkl oder
(2.45)
Bi j = Bi j,0 + ∆Bi j = Bi j,0 + πi jkl σkl
(2.46)
beschrieben werden. pi jkl ist dabei der photoelastische und πi jkl der piezooptische Tensor. Bi j,0 entspricht dabei den Brechungsindizes im unbelasteten Zustand, siehe Gleichung (2.40). Die Werte des
photoelastischen Tensors sind, ebenso wie die Indicatrix dimensionslos, während die Werte des piezooptischen Tensors die Einheit m2 /N besitzen. Beide Tensoren sind von vierter Stufe, müssen aber
bei der Verjüngung in die Voigtsche Notation unterschiedlich behandelt werden. Bei der Verjüngung
von pi jkl gilt, siehe [8]:
pmn = pi jkl für alle m und n.
(2.47)
Aus Symmetriegründen reduziert sich die Anzahl der unabhängigen Materialkonstanten von 34 = 81
auf 62 = 36. Die Anzahl der photoelastischen Konstanten in Abhängigkeit von den Kristallsystemen
ist in Tabelle 2.1 dargestellt. Gleichung (2.45) lautet in allgemeiner Form:
 

 
  p

B11
Bi j,0
ε1 = ε11
11 p12 p13 p14 p15 p16
 B   B
  p21 p22 p23 p24 p25 p26 

 
 22   i j,0  
 ε2 = ε22 



 



p31 p32 p33 p34 p35 p36 
 B33   Bi j,0  
ε3 = ε33 
 

=
+

.
(2.48)
·

 B   0  
p41 p42 p43 p44 p45 p46  
ε
=
2ε
4
23
 23  
 






 

 
 B13   0  
 p51 p52 p53 p54 p55 p56   ε5 = 2ε13 
p61 p62 p63 p64 p65 p66
B12
0
ε6 = 2ε12
Diese Gleichung gilt im Hauptachsensystem des dielektrischen Tensors, da hier Bi j,0 = 0 für i 6= j
gilt. Dabei muss das Hauptachsensystem dieses dielektrischen Tensors nicht mit dem Hauptachsensystem des Spannungs- bzw. Dehnungstensors übereinstimmen, siehe [20]. Nye definierte in [8] den
photoelastischen Tensor so, dass die Gleitungen, siehe Gleichungen (2.15) und (2.16), in die Berechnung der Indicatrix eingehen, siehe auch [21]. Diese Definition wird in der Fachliteratur als “Nye’s
convention” bezeichnet, siehe z.B. [20] und [22].
14
Man beachte auch, dass pi j im Gegensatz zur mechanischen Steifigkeit Ci j oder Si j , siehe Abschnitt
2.4.3, nicht symmetrisch sein muss. Bei der Verjüngung des piezooptischen Tensors muss aufgrund
der Scherdehnungen ein weiterer Faktor 2 eingefügt werden:
πmn = πi jkl wenn n = 1, 2, oder 3;
(2.49)
πmn = 2πi jkl wenn n = 4, 5, oder 6.
(2.50)
Damit gilt für die verjüngte Darstellung:
πmn = 1/2πnm wenn m = 4, 5, oder 6 und n = 1, 2, oder 3.
(2.51)
Diese Regel wurde in der Arbeit von Lü [23] übersehen, worauf in der späteren Arbeit von Chen [22]
hingewiesen wurde. Damit lautet Gleichung (2.46) in allgemeiner Form:
 
  π
 


π12
π13 π14 π15 π16
11
Bi j,0
B11
σ11

  π21
 B   B
π22
π23 π24 π25 π26  
σ22 

 22   i j,0  

 
 
 




π32
π33 π34 π35 π36   σ33 
 B33   Bi j,0   π31
+ 1
=
.


(2.52)
·

 B   0   π41 1 π42 1 π43 π44 π45 π46 

σ
23
23
  2
 



2
2


 


1
1
1
 
 B13   0  
 2 π51 2 π52 2 π53 π54 π55 π56   σ13 
1
1
1
0
B12
σ12
2 π61 2 π62 2 π63 π64 π65 π66
Wenn sich die elektromagnetische Welle in x3 -Richtung ausbreitet, lautet die Indicatrix für die x1 x2 -Ebene:
"
#
B11 B12
.
(2.53)
B21 B22
Durch den photoelastischen Effekt, welcher in allen Kristallklassen auftritt, wird der Brechungsindex
anisotrop, das heißt er wird an einem Punkt in verschiedenen Richtungen unterschiedlich groß. Grund
für die Änderung des Brechungsindexes an sich ist die Änderung des Atomabstandes aufgrund der
auftretenden mechanischen Felder. Bei stärker werdendem Druck auf den Kristall werden die Atome
mehr zusammengepresst und der Brechungsindex erhöht sich, siehe [9]. Da diese Änderung des
Atomabstandes aufgrund der Anisotropie der mechanischen Steifigkeit auch anisotrop geschieht, ist
der resultierende Brechungsindex folglich ebenfalls anisotrop.
Die Doppelbrechung ∆n, siehe auch Gleichung (2.41), ergibt sich dann aus den Eigenwerten dieser
Indicatrix, siehe [24]:
q
1 B11 + B22 −3/2
∆n =
(B11 − B22 )2 + 4B212 .
(2.54)
2
2
Im kubischen Kristallsystem sind Bi j,0 für i 6= j in jeder Richtung gleich groß und eine Änderung
dessen kann als
1
B + ∆B =
(2.55)
(n + ∆n)2
geschrieben werden. Damit gilt für hinreichend kleine Änderung von B für die Doppelbrechung
näherungsweise, siehe [20] und [22],
n3
(2.56)
∆n = − 0 ∆B.
2
15
Damit wird im Fall kubischen Materialverhaltens die gesamte Doppelbrechung, d.h. der Differenzen
der Brechungsindizes im Hauptachsensystem der Indicatrix folgendermaßen berechnet:
n3
∆n = 0
2
q
(B11 − B22 )2 + 4B212
(2.57)
mit n0 als (optisch isotropen) Brechungsindex im unbelasteten Zustand, siehe u.a. [22] und [25]. Man
beachte, dass in [21] in Gleichung (1) (entspricht hier Gleichung (2.57)) das Quadrat im ersten Term
der Wurzel vergessen wurde.
Indicatrix im YAG-Kristall
Analog zur mechanischen Steifigkeit reduziert sich die Anzahl der unabhängigen photoelastischen
Konstanten in den kubischen Kristallklassen 432, 43m und m3m auf drei. Zu beachten ist aber, dass in
den anderen beiden Kristallklassen 23 und m3, die ebenfalls zum kubischen Kristallsystem gehören,
die Anzahl der unabhängigen photoelastischen Konstanten vier beträgt, siehe [8].
Im YAG-Kristall lautet Gleichung (2.48) für die [100]-Schnittrichtung:
 

 
  p
0
0
0
B11
B0
11 p12 p12

 B   B  
p12 p11 p12 0
0
0  
 22   0  
 

 
 
 
p
p
p
0
0
0
 B33   B0  
12
12
11

 

 

·
 B  =  0 +
0
0
0 p44 0
0  
 23  
 
 

 
 
 
0
0
0
0
p
0
 B13   0  
44

 
0
0
0
0
0 p44
B12
0
ε1 = ε11

ε2 = ε22 


ε3 = ε33 
.
ε4 = 2ε23 


ε5 = 2ε13 
(2.58)
ε6 = 2ε12
Gleichung (2.52) wird analog dazu für die [100]-Schnittrichtung im YAG-Kristall reduziert.
Die Materialwerte von pi j für den Nd:YAG-Kristall sind für diese [100]-Schnittrichtung gemessen wurden, siehe [26]: p11 = −0.029, p12 = 0.0091 und p44 = −0.0615. Ist der Kristall in einer anderen Schnittrichtung geschnitten, ist pi j , bzw. pi jkl gemäß Gleichung (2.1) zu transformieren:
p0i jkl = aim a jn ako al p pmnop .
(2.59)
Analog wird πi j bzw. πi jkl transformiert. Wie bereits im Abschnitt 2.4.1 erläutert, bleibt als Freiheitsgrad noch die Drehung des Kristalls im Resonator um seine Längsachse um den Winkel Ψ. Die
Transformationen in die häufig verwendete [111]-Schnittrichtung bei YAG-Kristallen sind detailliert
z.B. in [20] und [22] beschrieben.
16
3 Eigenpolarisationszustände und deren
Auswirkungen in Festkörperlasern
3.1 Einleitung
Dieses Kapitel beschreibt zunächst die Berechnung von Eigenpolarisationszuständen in Laserresonatoren mit Hilfe des Jonesformalismus. Anschließend werden die möglichen Eigenmoden des
elektromagnetischen Feldes im Resonator kurz erwähnt. Die gegebenenfalls entstehenden Verluste durch die Eigenpolarisationszustände gehen dabei in die Dynamische Multimode Analyse, siehe [27], ein. Des Weiteren wird beschrieben, wie sich mit bestimmten Resonatoren unter Ausnutzung der spannungsinduzierten Doppelbrechung bevorzugte Polarisationszustände erreichen lassen.
3.2 Polarisation und Jonesformalismus
Zur Beschreibung des Polarisationsgrades einer elektromagnetischen Welle eines Lasers wird im allgemeinen der Stokesformalismus verwendet, siehe [17] und [28]. Diese Beschreibung ist leistungsbasiert, da die Leistung eines Lichtstrahls gemessen werden kann. Eine Messung des zeitlichen Verlaufs dieser elektromagnetischen Welle ist aufgrund der hohen Frequenzen nicht möglich. Änderungen des Polarisationszustandes, die mit dem Stokesvektor beschrieben werden, werden dabei mit
Hilfe der Müller-Matrizen berechnet. Für den Sonderfall einer vollständig polarisierten elektromagnetischen Welle kann auch der Jonesformalismus verwendet werden, welcher nicht leistungsbasiert,
sondern feldgrößenbasiert ist. Dieser wird in dieser Arbeit für den Fall einer sich paraxial ausbreitenden monochromatischen Welle angewendet. Dieser Formalismus wurde von Jones entwickelt, siehe
[29].
Beschreibung des Jonesformalismus
Den Polarisationsstatus einer monochromatischen elektromagnetischen Welle beschreibt der Jonesvektor E, siehe [30]:
"
# "
#
"
#
E1
E01 eiδ1
E01
E=
=
bzw. E =
.
(3.1)
E2
E02 eiΦ
E02 eiδ2
Darin sind E01 und E02 die Amplituden, δ1 und δ2 die Phasen des elektrischen Feldes und Φ die Phasendifferenz zwischen δ1 und δ2 . i ist imaginäre Zahl. Die Zeitabhängigkeit des elektromagnetischen
17
Feldes wird dabei vernachlässigt. Da das magnetische Feld stets senkrecht auf dem elektrischem
steht, wird nur das elektrische Feld betrachtet. Im Falle vom linear polarisierten Licht sind die beiden Amplituden E0 gleich groß und die Phasendifferenz beträgt 0 oder π. In x1 -Richtung polarisiertes
Licht besitzt das elektrische Feld E1,pol und in x2 -Richtung polarisiertes Licht E2,pol :
" #
" #
0
1
.
(3.2)
, E2,pol = E0
E1,pol = E0
1
0
Im Fall von radial und azimutal polarisiertem Licht sind die Amplituden ebenfalls gleich groß und
die zugehörigen Gleichungen für die normierten elektrischen Felder lauten:
!
x1
E0
Erad = q
und
(3.3)
x2
x12 + x22
!
−x2
E0
Eazi = q
,
(3.4)
x1
x2 + x2
1
2
wobei x1 und x2 die Koordinaten sind. In [31] wird das elektrische Feld für diese Polarisationszustände und deren Beschreibung als TEM-Moden angegeben. Die Überlagerung von linearen Polarisationszuständen zu Zirkularen ist in [32] beschrieben.
Elemente, die den Polarisationszustand ändern, werden durch die Jonesmatrix J beschrieben:
"
#
j11 j12
J=
.
(3.5)
j21 j22
Der Polarisationsstatus einer eingehenden Welle Ein ändert sich durch das Durchlaufen eines polarisationsändernden Elements zur ausgehenden Welle Eout folgendermaßen:
Eout = JEin .
(3.6)
Werden N solcher Elemente durchlaufen, sind die Jonesmatrizen Ji miteinander zu multiplizieren,
beginnend mit der letzten:
Jtotal = JN JN−1 ...J2 J1 .
(3.7)
In dieser Arbeit werden Dichroismus und Degeneration ignoriert, siehe [33]. Wird der Jonesformalismus zur Berechnung des Polarisationszustandes eines Resonators verwendet, muss dabei sowohl der Hin- als auch der Rückweg der Lichtwelle durch zweimaliges Aufsummieren berücksichtigt werden, siehe [30]. Der Laserkristall ist dabei für die Berechnung in mehrere Scheiben unterteilt, die numerisch als einzelne Elemente mit unterschiedlichen Jonesmatrizen behandelt werden.
Beispiele von Jonesmatrizen von polarisationsändernden
Elementen
Ein Verzögerungselement ändert die Phase, nicht die Amplitude, durch unterschiedliche Brechungsindizes. Diese Doppelbrechung wurde im Abschnitt 2.4.4 beschrieben. Die Jonesmatrix einer Verzögerungsplatte Jretard lautet im Hauptachsensystem der zugehörigen Indicatrix:
!
d
e−i2π λ nlangsam
0
Jretard =
,
(3.8)
d
0
e−i2π λ nschnell
18
wobei d die Dicke dieses Elements, λ die Wellenlänge der monochromatischen Welle und nlangsam
und nschnell die Brechungsindizes zu den zugehörigen Eigenwerten der Indicatrix Bi j , siehe Gleichungen (2.38) und (2.41), sind.
Die Jonesmatrizen eines idealen horizontalen JHP und eines idealen vertikalen Polarisators JV P lauten
"
#
"
#
1 0
0 0
JHP =
, JV P =
.
(3.9)
0 0
0 1
Diese Elemente dämpfen das elektrische Feld in allen Richtungen außer der Vorzugsrichtung komplett. Die Dämpfung einer Schwingungsrichtung kann z.B. durch das Verwenden eines Drahtgitterpolaristors oder von einer oder mehreren dielektrischen Platten im Brewsterwinkel geschehen, siehe
[17] und [30]. Trifft eine Welle in einem nicht senkrechten Winkel auf eine dielektrische Platte,
wird ein Teil des Lichtes reflektiert und der andere Teil transmittiert. Der parallele polarisierte Anteil wird dabei schwächer reflektiert. Entspricht der Einfallswinkel dem “Brewsterwinkel”, wird der
senkrecht zur Einfallsebene polarisierte Anteil (s-polarisierte) zum Teil reflektiert und der parallele
Anteil (p-polarisiert) ohne Verluste transmittiert. Die Transmission t des s-polarisiert Anteils lautet
dabei:
2n
t= 2
,
(3.10)
n +1
wobei n der Brechungsindex der zugehörigen dielektrischen Platte ist. Damit lauten die Jonesmatrizen für N solcher dielektrischen Platten im Brewsterwinkel:


 
2N
1
0
2n
0 
2N  , JV P =  n2 +1
JHP = 
.
(3.11)
2n
0
0
1
n2 +1
Die Jonesmatrix eines Rotators, der das elektrische Feld mit zugehöriger Phase um den Winkel φ
dreht, lautet:
"
#
cos φ sin φ
Jrot (φ ) =
.
(3.12)
− sin φ cos φ
Die Jonesmatrix für einen dielektrischen Spiegel lautet:
"
#
1 0
Jrot (φ ) = r
,
0 r
(3.13)
wobei r der Reflexionsgrad des Spiegels ist. Dabei wird angenommen, dass die Verluste beider
Vektorkomponenten gleich groß sind, siehe [34]. Im Freiraum wird folgende Jonesmatrix verwendet:
"
#
1 0
2πL
,
(3.14)
Jrot (φ ) = e λ
0 r
worin L die Länge des Freiraums und λ die Wellenlänge der elektromagnetischen Welle ist, siehe
[35]. Da aber sowohl der Spiegel, als auch der Freiraum keine Phasendifferenz im Resonator verursachen, sondern nur die Amplituden beider Polarisationen gleichsam dämpfen, werden sie in dieser
Arbeit nicht bei der Jonesanalyse berücksichtigt.
Bei der Multiplikation der gesamten Jonesmatrix nach Gleichung (3.7) ist zu beachten, dass dabei
19
sich die einzelnen Jonesmatrizen im selben Referenzkoordinatensystem befinden müssen. Zum Beispiel können die Hauptachsen der Indicatrix, welche zur Doppelbrechung führen, an jedem Punkt
unterschiedlich sein. Deshalb sind die lokalen Jonesmatrizen der Verzögerungselemente, siehe Gleichung (3.8) mit Hilfe der Eigenvektoren, nach Gleichung (2.1) in ein globales Referenzkoordinatensystem zu transformieren und erst anschließend zu multiplizieren.
Eigenzustände der gesamten Jonesmatrix
Aus den Eigenzuständen der gesamten Jonesmatrizen lassen sich die Eigenpolarisationen berechnen, was ausführlich in [30], [34] und [36] beschrieben ist. Es werden die Eigenwerte der gesamten
Jonesmatrix Jtotal , siehe Gleichung (3.7), berechnet:
s
(
j
+
j
)
( j11 − j22 )2
11
22
−
jtotal
=
−
+ j12 j21 und
(3.15)
2
4
s
( j11 + j22 )
( j11 − j22 )2
+
jtotal
=
+
+ j12 j21 .
(3.16)
2
4
Diese Eigenwerte zeigen die Phasenverschiebungen während eines vollen Resonatordurchlaufes an.
Durch polarisationsändernde Effekte werden die elektromagnetischen Felder innerhalb des Resonators gedreht. Sind diese nach einen vollen Resonatordurchlauf wieder in ihre Ausgangslage zurückgedreht, ist dieser Polarisationszustand ein Eigenpolarisationszustand des Resonators. Die beiden
−
+
komplexen Eigenwerte jtotal
und jtotal
entsprechen diesen beiden Eigenpolarisationszuständen. Der
Verlustfaktor V bzw. r pol und der Transmissionafaktor T einer jeden Eigenpolarisation ist definiert
als
∓
V ∓ = 1 − | jtotal
|2 = r pol und
∓
T =
∓
| jtotal
|2 .
(3.17)
(3.18)
Der größte Eigenwert weist die geringsten Verluste auf und entspricht demnach dem Eigenpolarisationszustand des Resonators, da dieser bevorzugt“verstärkt wird. Die zugehörigen komplexen
−
+”
und normierten Eigenvektoren Eeig
und Eeig
entsprechen den elektrischen Feldern, die nach einem
vollständigen Resonatordurchlauf wieder ihre Ausgangslage einnehmen:
!
!
−)
−)
Real
(E
Imag
(E
x
x
−
+i
und
(3.19)
Eeig
=
Real Ey−
Imag Ey−
!
!
Real (Ex+ )
Imag (Ex+ )
+
+i
.
Eeig =
(3.20)
Real Ey+
Imag Ey+
Dieser Algorithmus ist von Lumer, [37], in einem Resonator mit einem Nd:YAG-Kristall verwendet
worden. Dabei wurden aber analytische Formeln zur Berechnung der Indicatrix benutzt.
Die Verteilung der Verluste des bevorzugten Eigenpolarisationszustandes gehen in dieser Arbeit mit
in die Verlustterme der Ratengleichungen der Dynamischen Multimode Analyse“(DMA ) ein, siehe
”
Abschnitt 3.4. Wird bei der Berechnung der globalen Jonesmatrix aber keine Dämpfung berücksichtigt, sind beide Eigenwerte gleich groß und es tritt eine willkürliche Überlagerung dieser Eigenpolarisationszustände auf, siehe [30]. Aber in realen Laserresonatoren sind diese Eigenwerte unterschiedlich groß und ein Eigenpolarisationszustand wird bevorzugt.
20
Um zu analysieren wie stark der Laserkristall die Polarisation der Lichtwelle im Resonator ändert,
wird ein über den Querschnitt gewichteter Ablenkungswinkel αdevia folgendermaßen definiert:
Z
|< Ex1 ,Eres >|
1
αdevia =
T (x1 , x2 ) arccos
d (x1 , x2 ) ,
(3.21)
A A
kEx1 kkEres k
worin A der Flächeninhalt der Querschnittsfläche des Laserkristalls, Ex1 = (1, 0)T ein linear polarisierter Lichtstrahl entlang der x1 -Achse und Eres das elektrische Feld des Eigenpolarisationszustandes am Auskoppelspiegel ist.
3.3 Eigenmoden eines Resonator
Die elektromagnetischen Felder im Resonator werden als stehende Wellen betrachtet. Dabei können
verschiedene Eigenmoden auftreten. Sie durchlaufen diesen ohne ihre Form zu verändern; sie reproduzieren sich selbst. Diese Moden können durch Hermit- oder Laguerremoden beschrieben werden.
Deren Herleitung aus der Helmholtz-Gleichung ist in [17] beschrieben. Für einen Hermit-GaußStrahl lautet die komplexe Amplitude Ul,m der Mode (l, m):
√
√
W0
2x1
2x2
x2 + x22
Ul,m = Al,m [
]Gl [
]Gm [
] exp[− jkx3 − jk 1
+ j (l + m + 1) ζ (x3 )]. (3.22)
W (x3 )
W (x3 )
W (x3 )
2R(x3 )
Darin ist k die Wellenzahl, A ist die komplexe Einhüllende, W ist Strahlweite, Gl die Hermit-GausßFunktion, R ist der Wellenfrontradius und ζ (x3 ) = tan−1 (x3 /x3,0 ). Nur der Grundmode (0, 0) ist hier
rotationssymmetrisch.
Eine weitere Beschreibung der Eigenmoden ist durch die Laguerre-Gauß-Strahlen möglich. Dabei
wird die Helmholtz-Gleichung in Zylinderkoordinaten gelöst. Die komplexe Amplitude der LaguerreGauß-Strahlen lautet:
W0
r
2r2
r2
l
Ul,m (r, φ , x3 ) = Al,m [
]
Lm
exp − 2
W (x3 ) W (x3 )
W 2 (x3 )
W (x3 )
(3.23)
2
r
exp[− jkx3 − jk
− jlφ + j (l + m + 1) ζ (x3 )].
2R(x3 )
l die Laguerre-Polynome. Die Laguerre-Gauß-Strahlen sind rotationssymmetrisch. Für
Dabei sind Lm
l = m = 0 entspricht diese dem Gaußstrahl. Für l 6= 0 ist die Intensität in der Mitte des Zylinders 0,
siehe [17].
3.4 Dynamische Multimode Analyse mit
Polarisationsverlusten
Die Dynamische Multimode Analyse (DMA) von Wohlmuth ist in [27] und [12] ausführlich beschrieben und im Programm ASLD [38] implementiert. Die Deformationen der Endflächen und die
Änderung des Brechungsindexes aufgrund der Temperaturänderung werden mit einer Finte-ElementAnalyse numerisch gelöst. Mit einer Gaussmodenanalyse werden die Eigenmoden des Resonators
21
unter Berücksichtgung thermischer Aberration berechnet. Die optische Welle wird als dynamische
Superposition der Eigenmoden beschrieben. Diese Eigenmoden werden mit den Ratengleichungen
gekoppelt. Diese Ratengleichungen eines Dreilevel- bzw. eines Vierlevellasers werden mittels finiten Volumendifferenzen dreidimensional gelöst. Als Verlustwerte gehen dabei die Resonatorverluste
LRes = LRtrip +R = LRtrip −log (rr ) in die Berechnung der Resonatorlebenszeit
τ=
τr
LRes
(3.24)
ein. LRtrip sind dabei die allgemeinen Resonatorverluste und rr sind die Verluste durch den Ausgangsspiegel des Resonators.
In der vorliegenden Arbeit werden dieser Rechnung noch die Verluste rPol , welche durch den Polarisationsfilter entstehen, hinzugefügt, siehe Kapitel 3.2.
LRes = LRtrip + R = LRtrip − log (rr ) − log (rPol ) .
(3.25)
Durch die Verteilung der Verluste über den Querschnitt des Kristalls können bestimmte Eigenmoden
stärker oder schwächer angeregt werden. Die Summe der Leistungen der einzelnen Moden ergibt
die gesamte Ausgangsleistung. Aus der resultierenden Aufteilung der verstärkten Welle in diese
Einzelmoden wird die Strahlqualität berechnet.
3.5 Stabilität von Laserresonatoren
In diesem Abschnitt wird beschrieben, wie die Ergebnisse des Brechungsindexes in die Berechnung
des Strahlenverlaufs im Resonator eingehen und wie diese polarisationsabängig die Stabilität des Resonators beinflussen. Diese Vorgehensweise wurde bereits in [18] angewendet.
3.5.1 Parabolischer Fit
Die Anwendung des parabolischen Fits ist in [27] beschrieben. Da die Brechungsindizes zum einen
von der Schwingungsrichtung des elektromagnetischen Feldes im Resonator abhängen, korrespondieren unterschiedliche Polarisationseigenzustände mit unterschiedlichen Brechungsindizes, siehe
Abschnitt 2.4.4. Zum anderen ist der Brechungsindex aber auch von der Temperatur selbst abhängig,
siehe auch [39]. Damit kann der gesamte Brechungsindex ni j aus der Indicatrix der x1 -x2 -Ebene mit
Hilfe der mechanischen Spannungen σkl oder der mechanischen Dehnungen εkl mit Hilfe der Gleichungen (2.45) und (2.46) für kubische Kristallsysteme berechnet werden (siehe auch [24] und [39]
und Gleichung (2.56)):
dn0
1
(T − T0 ) δi j − n30 πi jkl σkl oder
dT
2
dn0
1
= n0 δi j +
(T − T0 ) δi j − n30 pi jkl εkl .
dT
2
ni j = n0 δi j +
(3.26)
ni j
(3.27)
0
Darin ist δi j das Kronecker-Delta und dn
dT die Änderung des Brechungsindexes aufgrund der Temperaturänderung. Im Falle eines kubischen Kristalls ist der Brechungsindex im unbelasteten Zustand
22
n0 in allen Richtungen gleich groß. Wie schon beim photoelastischen Effekt bewirkt die reine Temperaturänderung eine Änderung der Atomabstände im Kristall. Da der Wärmeausdehnungkoeffizient im kubischen YAG-Kristall aber isotrop ist, bewirkt eine Temperaturänderung in diesem eine
gleichmäßige Verschiebung der Atome in alle Richtungen; der Brechungsindex bleibt damit isotrop.
Für die Berechnung eines polarisationsabhängigen skalaren Brechungsindexes sind die Winkel der
Polarkoordinaten und der Polarisation zu definieren, siehe auch Abbildung 3.1:
ψ =
Winkel der Polarkoordinaten und
ϕ =
Winkel der Polarisation.
Die zentrale Längsachse des Laserkristalls ist dabei die x3 -Achse des Polarkoordinatensystems. Im
Abbildung 3.1: Definitionen des Polarkoordinatenwinkels ψ und des Polarisationswinkels ϕ, [18]
Fall von radialer Polarisation des elektromagnetischen Feldes ist der Polarwinkel mit dem Polarisationswinkel identisch : ϕ = ψ. Im Fall von azimutaler Polarisation steht das elektromagnetische
Feld stets senkrecht auf dem Polarwinkel: ϕ = ψ + π2 , siehe Abbildung 3.2. Folgender Ansatz aus
Abbildung 3.2: Schwingungsrichtung des elektrischen Feldes bei radialer und azimutaler Polarisation
[40] wird zur Berechnung des Brechungsindizes n(ϕ) in Abhängigkeit vom Polarkoordinatenwinkels
benutzt:
cos(ϕ)n(ϕ) = x1 und sin(ϕ)n(ϕ) = x2
(3.28)
Eingesetzt in Gleichung (2.40), lautet damit der polarisationsabhängige Brechungsindex in der x1 x2 -Ebene:
−1/2
n(ϕ) = (B11 ) cos2 (ϕ) + 2∆B12 cos(ϕ)sin(ϕ) + (B22 ) sin2 (ϕ)
,
(3.29)
mit:
Radialer Polarisation: ϕ = ψ und
23
Azimutaler Polarisation:ϕ = ψ + π2 .
3.5.2 ABCD-Matrixmethode und allgemeine Stabilität von
Laserresonatoren
Das Stabilitätsverhalten von Laserresonatoren wird mit Hilfe der Strahlenoptik berechnet. Dabei
wird von paraxialen Verhalten ausgegangen, d.h. dass die Abstandsänderung der Strahlen von der
Ausbreitungsrichtung (x3 -Richtung) klein gegenüber den anderen Längen, wie Linsendurchmesser,
Brennweiten und Resonatorlängen, sind. Diese Methode ist allgemein bekannt und z.B. in [1] und
[30] beschrieben. Für die Stabilität des gesamten Resonators werden die g1 und g2 -Faktoren verwendet, siehe [1] und [41]. In einem stabilen Resonator gilt:
0 ≤ g1 g2 ≤ 1.
(3.30)
In einem einfachen Resonator, bestehend aus zwei Spiegeln mit den Radien R1 und R2 und dem
Abstand L dieser beiden zueinander, sind dabei
g1 ≡ 1 −
L
L
und g2 ≡ 1 − .
R1
R2
(3.31)
Damit lässt sich ein Stabilitätsdigramm erstellen, mit dem das Stabilitätsverhalten abgelesen werden
kann, siehe Abbildung 3.3.
Abbildung 3.3: Stabiltätsdigramm eines passiven Resonators, angelehnt an [1]
24
Um g1 und g2 zu berechnen, wird die ABCD-Matrixmethode genutzt. In dieser Beschreibung ist
die Änderung des Strahlradius gegenüber der Strahllänge sehr klein. Ein Strahl wird dabei durch
seinen Abstand zur optischen Achse xi und seinem Anstieg αi dargestellt. Ein den Strahlenverlauf
änderndes Element wird dabei als ABCD-Matrix modelliert. Damit ändern sich x1 und α1 eines
einlaufenden Strahls zu x2 und α2 des aus dem optischen Element austretenden Strahls folgendermaßen:
#
# "
# "
"
A B
x1
x2
.
(3.32)
=
·
C D
α1
α2
Die verschiedenen optischen Elemente, wie Spiegel oder Linsen, besitzen verschiedene ABCDMatrizen, welche in der Fachliteratur, z.B. [30], angegeben sind. Es wird angenommen, dass die
Brechungsindizes im Laserkristall eine radiale Abhängigkeit über dem Querschnitt aufweisen. Aus
den berechneten numerischen Ergebnissen wird für jede Diskretisierungsscheibe ein parabolischer
”
Fit“durchgeführt, um die Gaussmoden zu berechnen, siehe [27]. Der radial abhängige Brechungsindex n (r) für die x1 , bzw. x2 -Richtungen lautet:
1
n2
n (r) = n0 − n2 r2 ; γ 2 ≡ ,
2
n0
(3.33)
wobei n0 die Brechungsindex in der Mittelachse des Kristalls und n2 ein konstanter Faktor für jeden
Fit ist. Damit wird jede Diskretisierungsscheibe als “Gaussian duct” behandelt und für jede eine eigene ABCD-Matrix berechnet. Die in dieser Arbeit verwendeten ABCD-Matrizen für einen Freiraum,
einen sphärischen Spiegel und den “Gaussian duct” lauten, siehe [41]:
"
#
1 L
Freier Raum:
,
(3.34)
0 1
"
#
1
0
Sphärischen Spiegel:
,
(3.35)
−2/R 1
#
"
sin(γx3 )
cos (γx3 )
n0 γ
.
(3.36)
Gaussian duct:
− (n0 γ) sin (γx3 ) cos (γx3 )
Bei mehreren optischen Elementen sind diese Matrizen zu multiplizieren. In einem Resonator sind
dabei alle optischen Elemente zwei mal zu berücksichtigen, da der Lichtstrahl sich hin und zurück
bewegt. Damit ergibt sich die resultierende ABCD-Matrix aus den einzelnen Matritzen AEP , BEP ,
CEP und DEP für den einmaligen Lauf von einem Spiegel zum anderen nach
#
"
# "
#"
A B
DEP BEP
AEP BEP
.
(3.37)
=
C D
CEP AEP
CEP DEP
Im paraxialen Fall und wenn die Determinante der resultierenden ABCD-Matrix Eins beträgt, gilt
als Kriterium für einen stabilen Resonator, siehe [17]:
1
| (A + D)| ≤ 1 oder |g1 g2 | ≤ 1
2
(3.38)
g1 = AEP und g2 = DEP .
(3.39)
mit
25
Diese Vorgehensweise ist ebenfalls in [41] beschrieben. Kogelnik stellte in [42] einen Überblick über
ABCD-Matrizen für ein und mehrere Moden bei paraxialer Approximation und deren Einfluss die
Resonatorstabilität auf.
3.5.3 Polarisationsabhängige Stabilität von
Laserresonatoren
Durch unterschiedliche Brechungsindizverläufe bei unterschiedlichen Polarisationszuständen, siehe
Gleichung (3.29), ergeben sich für demnach auch unterschiedliche ABCD-Matrizen für den gesamten Resonator - eine für die x1 -Richtung und eine für die x2 -Richtung, siehe Gleichung (3.32). Damit
kann der verstärkte Lichtstrahl eines bestimmten Polarisationszustandes im Resonator verbleiben,
während der Strahl des anderen Polarisationszustandes den Resonator verlässt, siehe Abbildung 3.4.
Der Resonator ist dann nur für einen bestimmten Polarisationszustand stabil. Mit dieser Vorgehensweise wurde bereits in [43] ein radial polarisierter Strahl erzeugt. Allerdings wurde dort die natürliche Doppelbrechung des Nd:YVO4 -Kristalls mit einbezogen. In [44] und [45] wurde experimentell
die Erzeugung von radial und azimutal polarisierten Licht mit Laserresonatoren mit einem Nd:YAGKristall durch die Nutzung der thermischen Linse beschrieben. Anders als z.B. in [46], sind damit
keine zusätzlichen optischen Elemente nötig.
Abbildung 3.4: Stabiler und instabiler Resonator, [18]
26
4 Verbesserung der Strahlqualität und
Ausgangsleistung durch Verwendung eines
Polarisationsfilters
4.1 Einleitung
Dieser Abschnitt baut hauptsächlich auf der Veröffentlichung [47] auf.
Brewsterplatten werden in Resonatoren mit Nd:YAG Kristallen im Allgemeinen eingebaut, um eine
linear Polarisation des Ausgangsstrahls zu erreichen, siehe [19]. Aber spannungsinduzierte Doppelbrechung führt zu einer Depolarisation vom Lichtstrahl innerhalb der Resonatoranordnung, das heißt,
dass keine ideale Polarisation des Ausgangsstrahls entsteht, siehe Abschnitt 3.2. Dies führt zu Leistungsverlusten an der Brewsterplatte und reduziert die Ausgangsleistung und die Strahlqualität. Um
diese Depolarisationseffekte zu untersuchen, wird für gewöhnlich der Jonesformalismus verwendet,
siehe [29]. In [34] wurden Jonesmatrizen für Resonatoren mit polarisationsändernden Elementen berechnet. Beispiele für Elemente, welche die Polarisation der elektromagnetischen Welle ändern sind
z.B. Glasplatten mit dem Brewsterwinkel (Brewsterplatten), Pockelszellen und Verzögerungsplatten. Die Eigenwerte der gesamten Jonesmatrix des gesamten Resonators werden zur Berechnung der
Verluste im Resonator verwendet. Zusätzliche Vergleiche mit experimentellen Ergebnissen zu den
Simulationen mit den Jonesmatrizen sind ebenfalls in [34] präsentiert. Diese Experimente beinhalteten einen Resonator mit einer Pockelszelle und einen Nd:YAG-Kristall. Der photoelastische Effekt
wurde dabei aber ignoriert.
In [48] wurde der photoelastische Effekt berücksichtigt. Dabei wurden analytische Formeln zur Berechnung der mechanischen Dehnungen im runden Nd:YAG-Kristall verwendet. Der quality dege”
neration factor “wurde dabei berechnet in dem Super-Gauß-Strahlen und Laguerre-Gauß-Strahlen
verwendet wurden. Depolarisationseffekte wurden in [49], [50] und [51] in Abhängigkeit von Kristallschnittrichtungen, Rotationswinkeln und Pumpstrahlprofilen untersucht. Aber auch in diesen
Veröffentlichungen wurden analytische Formeln für die Berechnung des photoelastischen Effekts
verwendet. Eine Zusammenfassung der Konzepte zur Berechnung der Eigenpolarisationszustände
von Resonatoren mit Nd:YAG-Kristallen und Brewsterplatten ist in [19] gegeben. Die darin enthaltenen Konzepte basieren auf analytischen Analysen des photoelastischen Effekts, der thermisch
induzierten Doppelbrechung, der Polarisationsverluste und der Ausgangsleistungsberechnung. Aber
diese analytischen Betrachtungsweisen unterliegen einigen Einschränkungen. Zum ersten wird dabei nur der TEM00 -Mode betrachtet und die Moden höherer Ordnung, die großen Einfluss auf die
Ausgangsleistung und Strahlqualität haben (siehe [27]), werden nicht berücksichtigt. Zum zweiten
erfordert eine analytische Berechnung der dreidimensionalen mechanischen Spannungs- und Dehnungsverläufe eine Annahme des zweidimensionalen ebenen Spannungszustandes“oder des zwei”
dimensionalen ebenen Dehnungszustandes“. Wenn bei einem Laserkristall dessen Länge sehr viel
”
27
kleiner als dessen übrigen Abmessungen ist, kann man näherungsweise von einen ebenen Spannungszustand ausgehen. Damit wird die Längsspannung im Kristall als 0 angenommen. Wenn dagegen die Länge des Kristalls sehr viel größer als dessen übrigen Abmessungen ist, geht man näherungsweise vom ebenen Dehnungszustand aus, das heißt, dass die Dehnung in Längsrichtungen als 0
angenommen wird. Des Weiteren sind bei beiden dieser Annahmen die Schubdehnungen und Schubspannungen in der axial-radial-Ebene ebenfalls 0, siehe auch [13]. Aber in [14] wurde gezeigt, dass
durch Vernachlässigung dieser Dehnungen, bzw. Spannungen, siehe Abschnitt 2.4.4, ungenaue Ergebnisse entstehen. Dies hat für den Fall der [111]-Schnittrichtung entscheidende Bedeutung, da hier
bei den genannten analytischen Annahmen eine radialsymmetrische Depolarisation berechnet wird,
siehe [21], und bei numerischen Berechnungen dagegen eine Dreifachsymmetrie der Depolarisation,
siehe [14], entsteht. Auch können bei analytischen Annahmen im Fällen von runden Laserkristallen im allgemeinen nur rotationssymmetrische Annahmen bezüglich der Temperaturverteilung und
damit der thermisch induzierten Doppelbrechungsverteilung getroffen werden. Um all diese Einschränkungen zu überwinden, sind vollständige numerische Analysen notwendig. Deshalb werden in
diesem Abschnitt die Verteilung der Temperatur und der strukturellen Mechanik mit einer dreidimensionalen Finite-Elemente-Analyse berechnet. Des Weiteren werden die Eigenpolarisationszustände
mit einer zweidimensionalen Jonesmatrixanalyse berechnet. Dieser vollständige numerische Ansatz
erlaubt die Analyse der Doppelbrechung innerhalb eines runden Nd:YAG-Kristalls in Abhängigkeit
von dessen Schnittrichtung und Rotationswinkel. Beispielhaft werden die [100]-, die [110]- und die
[111]-Schnittrichtung genau analysiert. Diese Untersuchung berücksichtigt die Scherdehnungen in
der axial-radial-Ebene, welche den bereits erwähnten signifikanten Einfluss auf den photoelastischen
Effekt, insbesondere im in [111]-Richtung geschnittenen Kristall, haben.
Dieses Kapitel zielt auf die Analyse eines Resonators mit Brewsterplatten darin. Der Jonesformalismus wird genutzt, um die Eigenwerte der Eigenpolarisationszustände im Resonator zu berechnen.
Diese Eigenwerte können als Verlustterme, welche durch die Brewsterplatten entstehen, aufgefasst
werden. Deshalb werden diese als zusätzliche Verlustterme in den Ratengleichungen zur Berechnung der Ausgangsleistungen einbezogen. Um die Ausgangsleistung zu berechnen, wird die Dynamische Moden Analyse (DMA) verwendet, welche in [27] beschrieben und angewendet worden
ist. Die Anwendung dieser Technik erlaubt die Berechnung von Ausgangsleistung und Strahlqualität des Resonators. Eine weitere Technik zur Analyse des Einflusses der Doppelbrechung ist die
Polarisationsreinheit. Dieser Wert ist der Abweichungswinkel der Eigenpolarisation zu einem ideal
polarisierten Licht, siehe Gleichung (3.21). Mit [49], [50] und [51] übereinstimmend hängen Polarisationsreinheit und Ausgangsleistung stark von der Pumpleistung und dem Kristallschnitt ab. Durch
die Anwendung der DMA wird zusätzlich gezeigt, dass die Strahlqualität ebenfalls von der Kristalldrehung beeinflusst wird.
4.2 Numerisches Modell
Die neue Simulationstechnik zur Berechnung der Eigenpolarisation wird an einem Resonator mit
Nd:YAG-Kristallen und zwei Brewsterplatten angewendet. Die [100]-, die [110]- und die [111]Schnittrichtungen der Kristalle mit unterschiedlichen Rotationswinkeln werden analysiert. Die mechanische Anisotropie des kubischen YAG-Kristalls wurde mit berücksichtigt, siehe Abschnitt 2.4.3.
Ausgangsleistung, Strahlqualität und Polarisationsreinheit werden in diesem Abschnitt verglichen
und diskutiert.
28
Abbildung 4.1: Laserresonator mit Endspiegel (HR), Auskoppelspiegel (OC) und dem Nd:YAGKristall. Dieser ist seitgepumpt. Die zwei Brewsterplatten (PB) befinden sich zwischen dem HR und dem Kristall, siehe [47].
In Abbildung 4.1 ist der aus dem Endspiegel (HR), dem Auskoppelspiegel (OC), dem Nd:YAGKristall und den beiden Brewsterplatten (BP) bestehende Resonator dargestellt. Die Dopingkonzentration der Nd3 + -Ionen im YAG-Kristall beträgt dabei 1%. Die Radien des HR und des OC sind
jeweils 3m. Die Reflektivität des OC ist 90%. Der Radius des Kristalls beträgt 2mm und dessen
Länge 20mm. Die Brewsterplatten sind aus BK-7-Glas hergestellt. Der zugehörige Brechungsindex
beträgt ηBP = 1.5068, siehe Gleichung (3.11). Zur Vereinfachung wird ein rotationssymmetrischer
Pumpstrahl mit einem gaußförmigen Pumpstrahl angenommen. Dessen Strahltaille beträgt 0.45mm.
Solch ein Pumpprofil kann aus seitlichem Pumpen angenommen werden. Alle Außenflächen des
Kristalls sind mechanisch frei, dass heißt, dass keine Oberflächenpunkte eingespannt sind. Die Seitenflächen sind auf eine konstante Temperatur von 293K gekühlt, während die Endflächen nicht
gekühlt sind. Der Laser selbst wird in cw-Mode betrieben, dass heißt, dass er kontinuierlich einen
Ausgangsstrahl abgibt.
Im kubischen Kristallsystem gibt es drei verschiedene Materialkonstanten für den mechanischen
Steifigkeitstensor. In Voigtscher Notation gilt (siehe Abschnitt 2.4.3) damit:
C11 = C22 = C33 ,
C12 = C13 = C23 , und
C44 = C55 = C66 .
(4.1)
29
(a)
(b)
Abbildung 4.2: (a) Zweidimensionales Gitter für den Jonesformalismus und (b) dreidimensionales
Finite-Elemente-Gitter, siehe [47].
Diese drei Werte sind in [52] für den YAG-Kristall gegeben:
C11 = 3.33 · 1011 N/mm2 ,
C12 = 1.11 · 1011 N/mm2 , und
C44 = 1.15 · 1011 N/mm2 .
(4.2)
Siehe dazu auch die Gleichungen (2.10) und (2.17).
Das zweidimensionale Gitter, welches für die Berechnung der Jonesmatrizen und damit der Eigenpolarisationszustände verwendet wird, ist in Abbildung 4.2(a) dargestellt. Für die Berechnung der dreidimensionalen Strukturmechanik wird in transversaler Richtung dasselbe Gitter angewendet, siehe
Abbildung 4.2(b).
4.3 Räumliche Verteilung der Temperatur, der mechanischen
Dehnungen und Spannungen
In Abbildung 4.3 ist der räumliche Temperaturverlauf dargestellt. Die maximale Temperatur beträgt
323K und tritt im Kern in Längsrichtung des Kristall auf, da hier sich die absorbierte Pumpleistung konzentriert. An den Seitenflächen liegt die Temperatur des Kristalls bei 293K, wie es von den
Randbedingungen vorgegeben ist. Aufgrund des rotationssymmetrischen Pumpenprofils ist auch die
Temperaturverteilung rotationssymmetrisch, da der Wärmeleitungskoeffizient im kubischen YAGKristall isotrop ist, siehe Abschnitt 2.4.2.
Ausgewählte mechanische Spannungen sind in Abbildung 4.4 dargestellt. Die Normalspannungen
σ1 und σ2 sind ebenso wie die Schubspannungen σ13 und σ23 aus Symmetriegründen jeweils gleich
30
Abbildung 4.3: Temperaturverlauf im seitgepumpten Kristall in K
groß. Die Normalspannungen σ1 , σ2 und σ3 sind aufgrund der Temperaturverteilung in der Mitte des
Kristalls am größten. Aus Symmetriegründen müssen die Schubspannungen in der Mitte null sein.
Auffallend ist, dass die Spannungen σ1 und σ3 trotz Anisotropie völlig symmetrisch erscheinen.
Grund dafür ist die nur schwach ausgeprägte mechanische Anisotropie im YAG-Kristall: Mit den
Materialwerten C11 und C12 , die in den Gleichungen (4.2) gegeben sind, lassen sich mit Hilfe der
Gleichungen (2.12) und (2.13) die mechanischen Werkstoffwerte für die isotrope Annahme für den
YAG-Kristall berechnen:
E = 2.775 · 1011 N/mm2 und
(4.3)
ν = 0.25.
(4.4)
Mit Gleichung (2.13) ergibt sich damit ein Schubmodul Giso für die isotrope Materialannahme:
Giso = 1.11 · 1011 N/mm2 .
(4.5)
Damit lässt sich ein Grad der Anisotropie definieren (siehe auch [14]):
C44 − Giso
= 0.035.
C44
(4.6)
Daher ist der Grad der Anisotropie im YAG-Kristall nur schwach ausgeprägt.
Die von Mises-Vergleichsspannung im globalen x1 -x2 -x3 -Koordinantensystem ist folgendermaßen
definiert, [53]:
r h
i
1
2 + τ2 + τ2 .
(σ11 − σ22 )2 + (σ22 − σ33 )2 + (σ33 − σ11 )2 + 3 τ23
(4.7)
σMises =
13
12
2
Diese ist für eine Pumpleistung von 75W in Abbildung 4.5 dargestellt. Die maximale auftretende
Vergleichsspannung tritt ebenfalls im Kern des Laserkristalls auf und beträgt 29.8N/mm2 und ist
damit wesentlich kleiner als die Bruchfestigkeit von zwischen 133N/mm2 und 531N/mm2 , welche
in [54] angegeben ist.
31
(a) σ1
(b) σ12
(c) σ13
(d) σ3
Abbildung 4.4: Ausgewählte mechanische Spannungen σ im Laserkristall bei 75W Pumpleistung in
N/mm2 .
Abbildung 4.5: Von Mises-Vergleichsspannung σMises im Laserkristall bei 75W Pumpleistung in
N/mm2 .
32
(a) [100]-Schnittrichtung
(b) [110]-Schnittrichtung
(c) [111]-Schnittrichtung
Abbildung 4.6: Räumliche Verteilung der Doppelbrechung ∆n in der x1 -x2 -Ebene im Laserkristall,
siehe [47].
4.4 Räumliche Verteilung der Doppelbrechung
In Abbildung 4.6 sind die Muster der räumlichen Verteilung der Doppelbrechung für die verschiedenen Schnittrichtungen wiedergegeben. Wie in [21], [49] und [50] mit analytischen Formeln berechnet, besitzt diese Doppelbrechung im Kristall der [100]-Schnittrichtung eine Vierfachsymmetrie und
im Fall einer [110]-Schnittrichtung eine Zweifachsymmetrie. Dies deckt sich mit den hier verwendeten Berechnungen mit numerischen Methoden. Es fällt aber auf, dass die mit numerischen Formeln
berechnete Doppelbrechung im Fall der [111]-Schnittrichtung nicht rotationssymmetrisch ist, wie
es mit analytischen Methoden der Fall ist, sondern eine Dreifachsymmetrie aufweist. Der Grund
dafür ist die Vernachlässigung der Schubdehnungen in der axial-radial-Ebene bei der analytischen
Betrachtung, wie bereits im Abschnitt 4.1 und in [14] erläutert wurde. Diese Dreifachsymmetrie der
Doppelbrechung ist einer der Gründe warum eine volle dreidimensionale Finite-Element-Analyse
notwendig ist, um die Eigenpolarisation möglichst exakt zu berechnen.
4.5 Eigenpolarisationszustände im Resonator ohne
Brewsterplatte
In diesem Abschnitt wird als erstes ein Resonator ohne Brewsterplatten bei 75W Pumpleistung betrachtet. Einziges polarisationsänderndes Element ist der Kristall, der einer spannungsinduzierten
Doppelbrechung unterliegt. Mit der Gleichung (3.8) wird die gesamte Jonesmatrix berechnet. Da
sich keine Brewsterplatten im Resonator befinden, sind die Eigenwerte nach den Gleichungen (3.15)
−
und (3.16) komplex und ergeben den Betrag 1. Das heißt, dass die Abweichungen von jtotal
und
+
jtotal zu reinen realen Eigenwerten der Depolarisation innerhalb des Resonators entsprichen. In Ab−
bildung 4.7 sind die Realteile der Eigenwerte jtotal
dargestellt, welche entsprechend Gleichung (3.15)
berechnet wurden. Die zugehörigen Eigenvektoren für die [100]-Schnittrichtung sind beispielsweise
in Abbildung 4.8 dargestellt. In dieser Darstellung ist
→
−
E=
E1
E2
!
:=
Real (E1 )
Real (E2 )
!
.
(4.8)
33
(a) [100]-Schnittrichtung, Ψ = 0◦ , 75W (b) [110]-Schnittrichtung, Ψ = 0◦ , 75W (c) [111]-Schnittrichtung, Ψ = 0◦ , 75W
Abbildung 4.7: Ausgewählte Realteile der Eigenwerte der Jonesmatrizen, welche zur azimutalen Eigenpolarisation des übertragenden Feldes bei 75W Pumpleistung im Resonator ohne
Brewsterplatten gehören, siehe [47].
−
E1 und E2 sind dabei die elektrischen Felder in x1 - und x2 -Richtung. Die Eigenwerte von jtotal
+
gehören zur azimutalen und jtotal
zur radialen Polarisation, wie in [55] beschrieben ist. Das Muster
der Realteile der Eigenwerte wird durch das Muster der Doppelbrechung verursacht. Da das Muster
der Depolarisation ebenfalls durch die Doppelbrechung bestimmt wird, zeigen die Depolarisationsmuster in [21], [49] und [50] entsprechend dasselbe Symmetrieverhalten. Zum Beispiel im Fall der
[100]-Schnittrichtung (Abbildung 4.7(a)) zeigt der Eigenpolarisationszustand eine Vierfachsymmetrie - das Malteserkreuz. Für einen in [110]-Richung geschnittenen Kristall zeigt das Muster eine
Zweifachsymmetrie, siehe Abbildung 4.7(b) und im Fall der [111]-Schnittrichtung eine annähernd
rotationssymmetrische. Aber in den vorherigen Abschnitten und in [14] wurde gezeigt das letztere
Schnittrichtung eine Dreifachsymmetrie aufweist. Aber in Abbildung 4.7(c) ist dieses Verhalten nur
sehr schwach ausgeprägt.
Bemerkungen zu den numerischen Resultaten
a) Im Fall des Resonators ohne Brewsterplatte sind die Eigenwerte der gesamten Jonesmatrix hinsichtlich ihrer azimutalen und radialen Eigenvektoren sortiert worden. Beim Beispiel der [110]Schnittrichtung führt dies zu numerischen Schwierigkeiten zwischen der azimutalen und der radialen
Orientierung des Vektorfeldes zu unterscheiden, siehe Abbildung 4.7(b). Dies ist der Grund für die
starken Abweichungen in der Mitte des Laserkristalls.
b) Die Abbildungen, welche die Vektorfelder der einzelnen Polarisationen darstellen, zeigen ein
starkes und ungefähr rechteckiges Gebiet in der Mitte des Kristalls. Dies sind Visualisierungseffekte, da das Vektorfeld mit Hilfe eines blockstrukturierten Gitters berechnet wurde, siehe Abbildung 4.2(a). Diese Visualisierungseffekte sind nicht durch irgendwelche numerischen Fehler entstanden.
34
(a) [100]-Schnittrichtung
(b) [110]-Schnittrichtung
Abbildung 4.8: Realteile der beiden Eigenvektoren der Jonesmatrizen bei einer [100]Schnittrichtung und Ψ = 0◦ mit 75W Pumpleistung im Resonator ohne Brewsterplatten. Diese Eigenpolarisationszustände gehören zu Abbildung 4.7(a), siehe
[47].
4.6 Eigenpolarisationszustände im Resonator mit
Brewsterplatte
In diesem Abschnitt werden die Auswirkungen verschiedener Rotationswinkel der Kristalle, abhängig von den Symmetrieeigenschaften ihrer Doppelbrechungsmuster, auf die Eigenpolarisationszustände untersucht.
Da ein in [100]-Richtung geschnittener Kristall zu einer Vierfachfachsymmetrie der Doppelbrechung führt, werden hier die Rotationswinkel des Kristalls innerhalb des Resonators Ψ = 0◦ und
Ψ = 45◦ betrachtet, siehe Gleichung (2.2). Die Auswirkungen der Rotationswinkel Ψ = 0◦ , Ψ = 45◦
und Ψ = 90◦ werden im Fall eines in [110]-Richtung geschnittenen Kristalls aufgrund seiner Zweifachsymmetrie untersucht. Eine annähernd rotationssymmetrische Depolarisation wird für einen in
[111]-Richtung geschnittenen Kristall erwartet. Deshalb wird in diesem Fall nur Ψ = 0◦ analysiert.
Dennoch ist es möglich, dass für andere Pumpkonfigurationen und andere Pumpleistungen, die Analyse der Rotation eines in [111]-Richtung geschnittenen Kristalls bedeutend ist. Grund dafür ist die
möglicherweise stärkere Ausbildung der Dreifachsymmetrie der Doppelbrechung, wie es in den vorherigen Abschnitten erläutert wurde.
Es wird angenommen, dass zwei Brewsterplatten zwischen dem Endspiegel und dem Kristall befestigt worden sind, wie es in Abbildung 4.1 zu sehen ist. Für das Erreichen einer möglichst reinen
radialen Polarisation des Ausgangsstrahls wäre die Montage der Brewsterplatten zwischen dem Kristall und dem Auskoppelspiegel sinnvoller. Aber um die depolarisierten Effekte der spannungsinduzierten Doppelbrechung besser untersuchen zu können, wurden die Brewsterplatten an die genannte
andere Position befestigt. Polarisationsändernde Elemente sind jetzt der Kristall, der einer span-
35
(a) [100]-Schnittrichtung, Ψ = 0◦ , 15W
(b) [100]-Schnittrichtung, Ψ = 45◦ , 15W
(c) [111]-Schnittrichtung, 15W
(d) [110]-Schnittrichtung, Ψ = 0◦ , 15W
(e) [110]-Schnittrichtung, Ψ = 45◦ , 15W
(f) [110]-Schnittrichtungut, Ψ = 90◦ , 15W
Abbildung 4.9: Betrag der Eigenwerte der Jonesmatrizen bei 15W Pumpleistung bei verschiedenen
Schnittrichtungen und Rotationswinkeln Ψ in Resonatoren mit Brewsterplatten. Die
lokal am höchsten auftretenden Werte entsprechen dem Transmissionsfaktor für die
DMA, siehe [47].
36
(a) [100]-Schnittrichtung, Ψ = 0◦ , 75W
(b) [100]-Schnittrichtung, Ψ = 45◦ , 75W
(c) [111]-Schnittrichtung, 75W
(d) [110]-Schnittrichtung, Ψ = 0◦ , 75W
(e) [110]-Schnittrichtung, Ψ = 45◦ , 75W
(f) [110]-Schnittrichtung, Ψ = 90◦ , 75W
Abbildung 4.10: Betrag der Eigenwerte der Jonesmatrizen bei 75W Pumpleistung bei verschiedenen
Schnittrichtungen und Rotationswinkeln Ψ in Resonatoren mit Brewsterplatten. Die
lokal am höchsten auftretenden Werte entsprechen dem Transmissionsfaktor für die
DMA, siehe [47].
37
(a) [100]-Schnittrichtung, Ψ = 0◦ , 15W
(b) [100]-Schnittrichtung, Ψ = 45◦ , 15W
(c) [111]-Schnittrichtung, 15W
(d) [110]-Schnittrichtung, Ψ = 0◦ , 15W
(e) [110]-Schnittrichtung, Ψ = 45◦ , 15W
(f) [110]-Schnittrichtung, Ψ = 90◦ , 15W
Abbildung 4.11: Übertragene Eigenvektoren der Jonesmatrizen bei 15W Pumpleistung für unterschiedliche Schnittrichtungen und Rotationswinkel Ψ im Resonator mit Brewster38
platten, siehe [47].
(a) [100]-Schnittrichtung, Ψ = 0◦ , 75W
(b) [100]-Schnittrichtung, Ψ = 45◦ , 75W
(c) [111]-Schnittrichtung, 75W
(d) [110]-Schnittrichtung, Ψ = 0◦ , 75W
(e) [110]-Schnittrichtung, Ψ = 45◦ , 75W
(f) [110]-Schnittrichtung, Ψ = 90◦ , 75W
Abbildung 4.12: Übertragene Eigenvektoren der Jonesmatrizen bei 75W Pumpleistung für unterschiedliche Schnittrichtungen und Rotationswinkel Ψ im Resonator mit Brewsterplatten, siehe [47].
39
nungsinduzierten Doppelbrechung unterliegt, und die beiden Brewsterplatten. Mit den Gleichungen
(3.8) und (3.11) wird demnach die gesamte Jonesmatrix berechnet. Damit wird das elektromagnetische Feld abgeschwächt und ein Eigenpolarisationszustand erfährt größere Verluste als der andere.
Abbildungen 4.9 und 4.10 zeigen die Beträge der Eigenwerte der Eigenpolarisationszustände für jeweils 15W und 75W Pumpleistung. Die zugehörigen Eigenvektoren sind in den Abbildungen 4.11
und 4.12 dargestellt. Die darin zu sehende Länge der Eigenvektoren ist proportional zum Transmissionsfaktor T , siehe Gleichung (3.18). Der lokale minimale absolute Wert von 0.52 ergibt sich, in
dem man den Brechungsindex der beiden Brewsterplatten von ηBP = 1.5068 in Gleichung (3.11) zur
Berechnung der Dämpfung mit Hilfe der Jonesmatrix einsetzt. Im Fall von idealen Polarisationsfiltern und abwesender Doppelbrechung ist ein Eigenpolarisationszustand linear zur x1 -Achse und der
andere linear zur x2 -Achse polarisiert. Aber in einem realen Resonator mit einem Polarisator rotiert
ein Nd:YAG-Kristall das elektrische Feld aufgrund der spannungsinduzierten Doppelbrechung. Dies
führt zu zwei verschiedenen Eigenpolarisationszuständen. Die zugehörigen Eigenwerte bilden zwei
voneinander getrennte Mannigfaltigkeiten im Fall von einem [100]-Schnitt, einem Rotationswinkel
von 45◦ und einer Pumpleistung von 15W , siehe Abbildung 4.9(b). Die zugehörigen Eigenvektoren,
welche zu den größeren Eigenwerten gehören, sind in Abbildung 4.11(b) dargestellt. Darin ist zu
sehen, dass diese Eigenvektoren hauptsächlich zur x1 -Achse polarisiert sind. Als Konsequenz sind
die Abweichungswinkel (siehe Gleichung (3.21)) nahe an 0◦ , siehe Abbildung 4.13. Allgemein gilt,
dass ein von Betrag 1 abweichender Eigenwert zu einem mehr in radialer oder azimutaler Richtung
orientierten Eigenvektor führt. Die anderen Fälle, als der gerade diskutierte Fall eines [100]-Schnitts
mit einem Rotationswinkel von 45◦ und einer Pumpleistung von 15W , sind in den übrigen Bildern
von den Abbildung 4.9 und 4.10 zu sehen. Darin ist festzustellen, dass die Eigenwerte sich nicht in
zwei von einander getrennte Mannigfaltigkeiten unterscheiden. Die verschiedenen Eigenpolarisationszustände, welche annähernd linear zur x1 -Achse bzw. zur x2 -Achse polarisiert sind, überschneiden sich. Deshalb steigt der aufintegrierte Abweichungswinkel, wie in Abbildung 4.13 dargestellt. In
Bereichen, wo der Betrag der höchsten Eigenwerte nahezu 1 beträgt, sind die Eigenvektoren nahezu
in x1 -Richtung polarisiert. Befinden sich diese aber im Überschneidungsbereich mit dem anderen Polarisationszustand, orientieren sich die Eigenvektoren in azimutaler bzw. radialer Richtung. Dies ist
besonders gut am Beispiel des in [110]-Richtung geschnittenen Kristalls mit einem Rotationswinkel
von 45◦ zu sehen, siehe Abbildungen 4.10(e) und 4.12(e).
4.7 Vergleich von Ausgangsleistung, Strahlqualität und
Polarisationsreinheit
In Abbildung 4.13 befindet sich der nach Gleichung (3.21) berechnete Abweichungswinkel αdevia in
Abhängigkeit von der Pumpleistung. Die Ausgangsleistung und die Strahlqualität, welche mit der
Dynamischen Multimode Analyse berechnet wurden (siehe [27]), sind in den Abbildungen 4.14,
4.15 und 4.16 dargestellt. Abweichungswinkel, Ausgangsleistung und Strahlqualität hängen stark
vom Rotationswinkel im Fall der [100]- und [110]-Schnittrichtung des Kristalls ab. Des Weiteren
hängen die Simulationsresultate vom Pumpradius und der Resonatorkonfiguration ab. Trotzdem stellt
sich heraus, dass ein in [100]-Richtung geschnittener Kristall mit einem Rotationswinkel von 45◦ eine höhere Ausgangsleistung und einen geringeren Abweichungswinkel bedingt. Grund für die hohe
Ausgangsleistung ist die bessere Verstärkung vieler TEM-Moden durch den geeigneten Transmissionsfaktor, als es bei den anderen Beispielen der Fall ist. Dies liegt an den hohen Eigenwerten
40
Abbildung 4.13: Gewichteter Abweichungswinkel αdevia (nach Gleichung (3.21)) der Polarisation im
Vergleich zu einem linear polarisierten Strahl entlang der x1 -Achse in Abhängigkeit
von der Pumpleistung in Resonatoren mit Brewsterplatten, siehe [47].
Abbildung 4.14: Ausgangsleistung der Resonatoren mit und ohne Brewsterplatten in Abhängigkeit
von der Pumpleistung, siehe [47].
41
Abbildung 4.15: Strahlqualität des Ausgangsstrahls in x1 -Richtung der Resonatoren mit und ohne
Brewsterplatten in Abhängigkeit von der Pumpleistung, siehe [47].
Abbildung 4.16: Strahlqualität des Ausgangsstrahls in x2 -Richtung der Resonatoren mit und ohne
Brewsterplatten in Abhängigkeit von der Pumpleistung, siehe [47].
42
in der Querschnittsmitte des Kristalls, was die hohen Transmissionsfaktoren bedingt, siehe dazu
auch Abbildung 4.10(b). Die Beteiligung mehrerer Moden hat jedoch eine schlechtere Strahlqualität zur Folge, siehe [27]. Eine bessere Strahlqualität kann durch die Verwendung eines in [110]Richtung geschnittenen Kristalls mit optimalen Rotationswinkel erreicht werden. Im Fall von einem
Rotationswinkel von 90◦ tritt dabei die beste Strahlqualität in x1 -Richtung auf, was auf eine nahezu alleinige Verstärkung der TEM00 -Mode zurückzuführen ist. Ist der Laserkristall dagegen in
[110]-Richtung geschnitten und unterliegt einem Rotationswinkel von 45◦ , wird der TEM00 -Mode
kaum verstärkt. Grund dafür sind die niedrigen Beträge der Eigenwerte in der Mitte des Kristallquerschnitts (siehe Abbildung 4.10(e)), wo die Intensität des Grundmodes am höchsten ist. Dies hat
zur Folge, dass die Ausgangsleistung niedrig und die Strahlqualität schlecht gegenüber den anderen
Fällen ist.
4.8 Zusammenfassung und Schlussfolgerung
In diesem Kapitel wurden Eigenpolarisationszustände aufgrund von spannungsinduzierter Doppelbrechung in Resonatoren mit Nd:YAG-Kristallen sowie mit und ohne Brewsterplatten berechnet.
Dazu wurde eine dreidimensionale Finite-Element-Analyse für die Strukturmechanik und eine zweidimensionale Jonesmatrixanalyse durchgeführt. Diese Untersuchungen zeigen, dass Polarisationsreinheit, Ausgangsleistung und Strahlqualität von der Schnittrichtung des Kristalls und seinem Rotationswinkel abhängen. Bezüglich Ausgangsleistung und Abweichungswinkel von idealer linearer
Polarisation stellte sich der in [100]-Richtung geschnittene Kristall mit einem Rotationswinkel von
45◦ heraus. Bei anderen Resonatorkonfigurationen könnten aber andere Schnittrichtungen und Rotationswinkel zu optimalen Ergebnissen führen. Dies zeigt, dass die Optimierung von Laserresonatoren
kein einfaches Problem ist. Letztlich hat diese Untersuchung gezeigt, dass numerische Simulationen
ein wirkungsvolles Hilfsmittel zur Optimierung eines Laserdesigns sind.
43
44
5 Erzeugung eines bestimmten
Polarisationszustandes mittels Stabilität
des Resonators
5.1 Einleitung
Für bestimmte Anwendungen ist radial oder azimutal polarisiertes Laserlicht nötig. Dies wird häufig
durch den Einbau von zusätzlichen optischen Elementen in Laserresonatoren erreicht. In diesem
Kapitel wird beschrieben, wie eine solche Polarisation ohne zusätzliche optische Elemente durch
Ausnutzung der spannungsinduzierten Doppelbrechung in einem Festkörperlaserresonator mit einem Nd:YAG-Kristall erzeugt werden kann. Es wird dabei untersucht, welchen Einfluss der Kristallschnitt und die Kristalldrehung auf die Ausgangsleistung und die Strahlqualität haben.
In einem doppelbrechenden Medium ist der Brechungsindex nicht isotrop, sondern für unterschiedliche Schwinungsrichtungen des elektromagnetischen Feldes unterschiedlich, siehe Abschnitt 2.4.4
und [17]. Es wird in einen ordentlichen“und in eine außerordentlichen“Strahl unterschieden, wel”
”
che senkrecht aufeinander stehen. Diese werden in einem doppelbrechenden Medium unterschiedlich
stark abgelenkt. Im Fall von optisch positiver Doppelbrechung ist no < ne und im Fall von negativer
Doppelbrechung ist no > ne , wobei no der Brechungsindex des ordentlichen und ne der Brechungsindex des außerordentlichen Strahls ist. Aufgrund dieser unterschiedlichen Ablenkung der beiden
Strahlen läßt sich ein Resonator bauen, in dem nur einer dieser beider Strahlenverläufe stabil ist,
d.h. dass der andere Strahl nach ein paar Umläufen im Resonator diesen verlassen und damit nicht
verstärkt wird. Da diese beiden Strahlverläufe unterschiedlichen Polarisationszuständen zugeordnet
werden können, emittiert dieser Resonator damit nur Licht einer bestimmten Polarisation. Mit Laserkristallen, die eine natürliche Doppelbrechung besitzen, ist dieses Prinzip ohne den Einbau zusätzlicher optischer Elemente leicht zu realisieren, wie es z.B. bei einem (tetragonalen) Nd:YVO4 -Kristall
in [43] dargestellt ist. Bei diesem Beispiel wird in diesem optisch einachsig positiven Kristall nur der
außerordentliche Strahl verstärkt, welcher der radialen Polarisation entspricht. Das heißt das “ordentliche Feld” ist azimutal und das “außerordentliche Feld” ist radial polarisiert, siehe [43] und [55].
Damit wird dieser Polarisationszustand ohne weitere optische Elemente, wie z.B. Verzögerungsplatten oder Polarisationsfilter, erreicht.
Mit Hilfe von optischen Elementen wurden bereits azimutale und radiale polarisierte Laserstrahlen
in Resonatoren mit Nd-YAG-Kristallen erzeugt: In [56] wurden polarisationsselektierende Spiegel
verwendet, um nur das Licht der gewünschten Polarisation zu reflektieren.
Der YAG-Kristall gehört dagegen dem kubischen Kristallsystem an und besitzt keine natürliche Doppelbrechung, siehe Abschnitt 2.3. Dort tritt im Laserbetrieb nur die thermisch induzierte Doppelbrechung auf, wie in Abschnitt 2.4.4 erläutert. In [44] und [45] wurde bereits experimentell demonstriert, wie ein bestimmter Polarisationszustand durch geeignete Stabilität des zugehörigen Strahlen-
45
verlaufs erreicht werden kann. Theoretische Analysen und Vergleiche mit experimentellen Ergebnissen zur Stabilität von Resonatoren mit azimutal oder radial polarisierten Lasermoden wurden in [57]
durchgeführt. Dabei wurde eine Blende im Resonator zur geeigneten Selektion von LaguerremodenEigenmoden (LG-Moden) verwendet. Die Auswahl der Moden bezüglich des azimutalen oder radialen polarisierten Lichts fand mit Hilfe der thermischen Linse, welche für die beiden Polarisationen
unterschiedlich ist, statt. Die in der dortigen Arbeit, [57], verwendete thermische Linse, siehe [1],
basiert aber auf analytischer Betrachtung des photoelastischen Effektes. Dessen Auswirkung auf die
Stabilität wurde auch in [58] untersucht.
In diesem Abschnitt wird nun an einem eigenen Beispiel das Stabilitätsverhalten mit Hilfe numerischer Methoden genauer untersucht und Aussagen über die resultierende Strahlqualität gewonnen.
Im Abschnitt 3.5.2 wurde die Berechnung des Stabilitätsverhaltens von Laserresonatoren bereits beschrieben.
5.2 Numerisches Modell
Das numerische Modell, welches für die Untersuchungen der Stabilitätsbereiche erstellt wurde, ist
in Abbildung 5.1 dargestellt. Der Kristall ist 8mm lang und besitzt einen Durchmesser von d = 4mm.
Die Dopingkonzentration der Nd3 + -Ionen im YAG-Kristall beträgt 1%. Sowohl der Endspiegel, als
auch der Auskoppelspiegel weisen eine Krümmung von R = −0.25mm auf. Das bedeutet, dass diese Spiegel konvex sind. Der Kristall ist über die gesamte Länge seitlich gepumpt. Es wird eine
gaußfömige Verteilung des Pumpstrahls angenommen, dass heißt, dass der supergaußsche Exponent 2 beträgt. Die Strahltaille ist dabei 0.35mm. Der Abstand zwischen dem Endspiegel und dem
Kristall ist bei der Untersuchung der Stabilitätsbereiche stets genauso groß wie der Abstand zwischen dem Kristall und dem Auskoppelspiegel. Alle anderen Parameter bleiben unverändert. Zwar
wurde in [59] gezeigt, dass die Stabilitätsbereiche sehr stark von der Pumpleistung abhängen, aber in
diesem Beispiel wird nur der Einfluss der unterschiedlichen Kristallschnittrichtungen und Kristalldrehungen im Resonator bei konstanter Pumpleistung untersucht. Demnach werden im Folgenden
alle Ergebnisse, wie z.B. die Strahlqualität und der Strahlradius, in Abhängigkeit von der gesamten Resonatorlänge LRes angegeben. Abhängigkeiten von Pumpleistung und Kristallbeschaffenheit
könnten Gegenstand zukünftiger Forschung sein. Eine Draufsicht des verwendeten blockstrukturierten Gitters ist in Abbildung 5.2(a) gezeigt; eine perspektivische Ansicht in Abbildung 5.2(b). Die
Seitenflächen des Kristalls sind auf 293K gekühlt, während die Endflächen nicht gekühlt sind. Des
Weiteren sind alle Flächen des Kristalls mechanisch frei, das heißt, dass Verschiebungen der Knoten
an der Kristalloberfläche in alle Richtungen möglich ist. Der Kristall ist seitgepumpt und die Pumpleistung beträgt 70W . Auch dieser Laser wird in cw-Mode betrieben, das heißt, dass ein kontinuierlicher Ausgangsstrahl entsteht. Das mechanische Materialverhalten wird, wie im letzten Kapitel, als
anisotrop angenommen.
46
Abbildung 5.1: Laserresonator mit Endspiegel (HR), Auskoppelspiegel (OC), und dem Nd:YAG Kristall. Der Kristall ist seitgepumpt. Die Abstände zwischen dem HR und dem Kristall
bzw. zwischen dem OC und dem Kristall sind immer gleich groß.
(a)
(b)
Abbildung 5.2: (a) Draufsicht des Gitters und (b) perspektivische Ansicht des Gitters.
47
5.3 Temperaturverlauf und mechanische
Spannungen
Der Temperaturverlauf im Kristall während des Laserbestriebes ist in Abbildung 5.3 dargestellt.
Wie von den Randbedingungen vorgeben, beträgt die Temperatur an den Seitenflächen 293K. Aufgrund des rotationssymmetrischen Pumpens mit der höchsten Absorption in der Kristallmitte ist
die Temperatur mit ca. 345K in der Mitte am höchsten. Da in dem hier verwendeten Modell keine
Rückkopplung der resultierenden Brechungsindizes auf das Absorptionsprofil des Kristalls berücksichtigt wird, ist hier dieser Temperaturverlauf für jedes Rechenbeispiel gleich. Die räumlichen
Verläufe der mechanischen Spannungen sind qualitativ mit denen aus dem vorherigen Kapitel 4
vergleichbar, siehe dazu die Abbildungen 4.4 und 4.5. Die von Mises-Vergleichsspannung von diesem Beispiel, siehe Gleichung (4.7), ist in Abbildung 5.4 zu sehen. Sie ist auch bei diesem Beispiel
aufgrund der geringen mechanischen Anisotropie annähernd rotationssymmetrisch, siehe Abschnitt
4.3.
Abbildung 5.3: Temperaturverlauf im Laserkristall in K.
48
Abbildung 5.4: Mechanische von Mises-Vergleichsspannungen im Laserkristall in N/mm2 .
49
5.4 Räumlich Verteilung der Brechungsindizes
In Abbildung 5.5 ist die Änderung des Brechungsindexes nur aufgrund der Temperatur ∆ntherm dargestellt. Diese Änderung wird nach folgender Formel berechnet:
∆ntherm =
dn0
(T − T0 ) .
dT
(5.1)
Siehe dazu auch Gleichung (3.26) oder (3.27). Da hier ein linearer Zusammenhang zwischen der
Änderung der Temperatur und der Änderung des thermischen bedingten Brechungsindexes angenommen wird, ist ∆ntherm der Änderung der Temperatur T −T0 proportional. Der höchste Brechungsindex aufgrund der Temperatur tritt demnach in der Mitte auf. Man beachte dabei, dass diese Brechungsindexänderung einem Skalar entspricht, das heißt, dass der Brechungsindex damit noch isotrop bleibt. Da diese Änderung aufgrund von Gleichung (5.1) viel größer als die Änderung durch
den photoelastischen Effekt ∆nmech ist, siehe Gleichung (2.54), dominiert die Brechungsindexänderung aufgrund der reinen Temperaturänderung den parabolischen Fit dieser Indizes, siehe Abschnitt
3.5.2.
Abbildung 5.5: Brechungsindexänderung ∆ntherm im Laserkristall aufgrund des thermischen Feldes.
Durch den photoelastischen Effekt wird der Brechungsindex jedoch anisotrop, das heißt, dass dieser
an jedem Punkt auch von der Schwingungsrichtung der elektromagnetischen Welle abhängt. Mit Hilfe von Gleichung (3.29) lässt sich der an sich anisotrope Brechungsindex polarisationsabhängig als
ein skalarer Wert beschreiben. In Abbildung 5.6(a) ist ein Beispiel für die Änderung des Brechungsindizes in radialer und in 5.6(b) ein Beispiel in azimutaler Richtung dargestellt. Die überlagerten
50
(a) In radialer Richtung
(b) In azimutaler Richtung
Abbildung 5.6: Brechungsindexänderung ∆nmech im Laserkristall aufgrund des mechanischen Feldes.
Brechungsindizes aus n0 , den thermischen und photoelastischen Anteilen nach Gleichung (??) sind
für die radiale Richtung in Abbildung 5.7(a) und in azimutaler Richtung in Abbildung 5.7(b) zu sehen. Dieser Verlauf fließt anschließend in den parabolischen Fit zur Berechnung des Strahlverlaufs
im Kristall, siehe [27]. Bei dem Vergleich von Abbildungen 5.5 und 5.6 ist zu erkennen, dass der allein thermische Anteil dominiert, aber auch, dass der photoelastische Anteil dennoch zu einem deutlichen Unterschied des Brechungsindizesverlauf führt. Der parabolische Fit wird dabei zum einen
für die x1 -Achse und zum anderen für die x2 -Achse durchgeführt. Aber bei diesem parabolischen
Fit wird davon ausgegangen, dass die Hauptachsen der Indicatrix annähernd mit den globalen x1 x2 -Koordinatensystem übereinstimmen. Wären die Nebendiagonalelemente der Indicatrix sehr groß,
siehe Gleichung (2.53), müssten die Achsen des parabolischen Fit der Hauptachsen der Indicatrix
angepasst werden.
(a) In radialer Richtung
(b) In azimutaler Richtung
Abbildung 5.7: Gesamter Brechungsindex im Kristall aufgrund der thermischen und mechanischen
Felder.
51
5.5 Doppelbrechungsmuster
Entscheidend für einen möglichst großen Unterschied der Stabilitätsbereiche ist ein möglichst großer
Unterschied zwischen den Brechungsindizes der beiden senkrecht aufeinander stehenden Richtungen an einem räumlichen Punkt. Dieser Unterschied entsteht in diesem Beispiel beim kubisch YAGKristall durch die spannungsinduzierte Doppelbrechung, siehe Abschnitt 2.4.4. Diese ist für das hier
verwendete numerische Beispiel in Abbildung 5.8 dargestellt.
Abbildungen 5.8(a) und 5.8(a) weisen für den in [100]-Richtung geschnittenen Kristall die im vorherigem Kapitel schon erwähnte Vierfachsymmetrie in der x1 -x2 -Ebene auf. Dieses Muster ist in dem
um Ψ = 45◦ gedrehten Kristall ebenfalls deutlich zu sehen.
Im Fall des in [110]-Richtung geschnittenen Kristalls ist in den Abbildungen 5.8(c), 5.8(d) und 5.8(e)
die Zweifachsymmetrie der Doppelbrechung zu erkennen. Mit der Untersuchung der drei Rotationswinkel Ψ = 0◦ , Ψ = 45◦ und Ψ = 90◦ sind die größtmöglichen Auswirkungen auf das Stabilitätsverhalten dieser Kristallschnittrichtung abgedeckt.
Beim in [111]-Richtung geschnittenen Kristall in Abbildung 5.8(f) ist die typische Dreifachsymmetrie, siehe [14], zu sehen. Diese tritt besonders in den Endregionen des Kristalls auf, da hier die zugehörigen Schubspannungen in der axial-radial-Ebene am größten sind. Die Winkelabhängigkeit der
Doppelbrechung ist hier aber nicht so groß wie bei den anderen Schnittrichtungen. Deshalb wird bei
diesem Anwendungsbeispiel keine Variation des Rotationswinkels im Falles des in [111]-Richtung
geschnittenen Kristall durchgeführt.
In allen Fällen ist der Maximalwert der Doppelbrechung in etwa gleich groß. Grund hierfür ist, dass
aufgrund der nur schwach ausgeprägten mechanischen Anisotropie die Dehnungen bzw. Spannungen im Polarkoordinatensystem nahezu rotationssymmetrisch auftreten und dass die Maxima des
damit zu multiplizierenden photoelastischen Tensors, siehe Gleichung (2.48), durch die schnittrichtungsabhängige Rotation um die Mittelachse nur gedreht werden. Die teils ähnlichen und teils unterschiedlichen Minimalwerte sind möglicherweise auf numerische Fehler in der Berechnung zurückzuführen.
52
(a) [100]-Schnittrichtung, Ψ = 0◦
(b) [100]-Schnittrichtung, Ψ = 45◦
(c) [110]-Schnittrichtung, Ψ = 0◦
(d) [110]-Schnittrichtung, Ψ = 45◦
(e) [110]-Schnittrichtung, Ψ = 90◦
(f) [111]-Schnittrichtung, Ψ = 0◦
Abbildung 5.8: Doppelbrechung des Laserkristalls in Abhängigkeit von den einzelnen Schnittrichtung und Kristalldrehungen.
53
5.6 Laguerre-Mode-Profile
Es wurden Laguerre-Moden bis zur dritten Ordnung modelliert. Die Profile (0,0), (1,0), (2,0) und
(3,0) wurden dabei nicht berücksichtigt, da das elektromagnetische Feld dieser Moden in der Mitte von null verschieden ist, siehe auch Abschnitt 3.5.3. In einer radial oder azimutal polarisierten
elektromagnetischen Welle muss die Intensität im Mittelpunkt aber 0 sein um die Bedingung der Rotationssymmetrie zu erfüllen. Deswegen wurden die Ausgangsleistungen dieser benannten Moden
hier bei der Berechnung der Gesamtausgangsleistung auf 0 gesetzt. Als Beispiele sind hier die Intensitäten der resultierenden Moden (0,1), (0,2), (0,3), (1,1), (1,2) und (1,3) in Abbildung 5.9 dargestellt.
Deren Intensität ist in der Kristallmitte 0.
(a) Mode (0,1)
(b) Mode (0,2)
(c) Mode (0,3)
(d) Mode (1,1)
(e) Mode (1,2)
(f) Mode (1,3)
Abbildung 5.9: Muster ausgewählter Laguerre-Moden im Laserkristall.
54
5.7 Länge der Stabilitätsbereiche
Wie in Gleichung (3.30) im Abschnitt 3.5.2 beschrieben ist, muss das Produkt der g-Faktoren bei
einem stabilen Resonator kleiner gleich den Betrag von 1 ergeben. Aufgrund möglicherweise unterschiedlicher ABCD-Matrizen für die x1 - und x2 -Richtung können die g-Faktoren auch für die
verschiedenen Richtungen unterschiedlich sein. In diesem Fall muss trotzdem in beiden Raumrichtungen jeweils die Gleichung (3.30) erfüllt sein.
In Abbildung 5.10 sind die maximalen Produkte der g-Faktoren für die Resonatorlängenbereiche
dargestellt, worin nur der radiale Polarisationszustand stabil ist. Darin ist zu sehen, dass bei kleiner werdenden Resonatorlängen das Maximum des Betrages der Produkte der g-Faktoren über 1
steigt und damit der Resonator instabil wird. In dem Bereich der alleinigen radialen Polarisation
wird der Grundmode, welcher in der Querschnittsmitte eine von 0 verschiedene Intensität aufweist,
noch nicht verstärkt, siehe [43]. Bei den größer werdenden Resonatorlängen werden dann auch die
g-Faktoren für den azimutalen Polarisationszustand stabil. Der Grundmode, welcher keine reine zirkulare Polarisation mehr zulässt, wird nun ebenfalls verstärkt. In manchen Fällen wird bei steigender
Resonatorlänge der azimutale Polarisationszustand ebenfalls stabil, aber die zu dieser Polarisation
gehörende Ausgangsleistung liegt noch bei null, ehe der Resonator weiter an Länge zunimmt. Dieser
Bereich wird in dieser Arbeit zu dem Bereich alleinig auftretender radialer Polarisation zugerechnet.
Umgekehrt gibt es aber auch Bereiche, in denen der radiale Polarisationszustand zwar ebenfalls noch
stabil ist, aber keine zugehörige Ausgangsleistung auftritt. Dieser Bereich gehört damit zum allein
azimutalen Stabilitätsbereich.
Das entsprechende Diagramm für die azimutale Polarisation befindet sich in Abbildung 5.11. Dort
wird erst mit länger werdendem Resonator die azimutale Polarisation alleinig stabil. Bei noch weiter steigender Resonatorlänge werden dann auch hier die Produkte der g-Faktoren vom Betrag her
größer als 1 und der Resonator ist für alle Polarisationszustände instabil.
Die Längenbereiche, in denen nur ein Polarisationszustand stabil ist, variieren mit Kristallschnitt
und -drehwinkel. Ein Überblick über diese Bereiche ist in Abbildung 5.12 dargestellt. Den kleinsten
Bereich, wo nur ein Polarisationszustand stabil ist, weist der in [111]-Richtung geschnittene Kristall
auf. Größere Bereiche einer stabilen Polarisation sind beim in [100]-Richtung geschnittenen Kristall
präsent. Dabei unterscheiden sich die Ergebnisse eines Rotationswinkels des Kristalls um Ψ = 0◦
und Ψ = 45◦ kaum. Beim [110]-Schnitt treten die größten Bereiche auf, an denen nur ein Polarisationszustand stabil ist. Dabei sind die Ergebnisse auch stark von der Kristallrotation abhängig. Bei
einem Rotationswinkel von Ψ = 45◦ sind die Bereiche, wo nur ein Polarisationszustand stabil ist, am
größten. Der Grund für diese unterschiedlichen Resonatorlängen, in denen nur ein Polarisationszustand stabil ist, liegt an der verursachenden Doppelbrechung. Je größer der Unterschied zwischen den
Brechungsindizes der einzelnen Polarisationsrichtungen ist (siehe Gleichung (3.29)), desto größer
sind auch die Unterschiede der Stabilitätsbereiche. In [21] wurde ein “Doppelbrechungsparameter”
(birefringence parameter) eingeführt und bildlich dargestellt, um die Doppelbrechung geometrie- und
materialunabhängig zu quantifizieren. Diese Parameter sind in Fig. 3 in [49] für die verschiedenen
Kristallschnitte zusammengefasst. Auch wenn dort von einem isotropen Materialmodell ausgegangen wird und analytische Formeln verwendet wurden, zeigen die Ergebnisse dort ausreichend genau,
dass bei einem [111]-Schnitt der Doppelbrechungsparameter (nahezu) rotationswinkelunabhängig
ist. Beim [100]-Schnitt war der Doppelbrechungsparameter deutlich rotationswinkelabhängig und
zeigte die bekannte Vierfachsymmetrie. Im Falle des in [110]-Schnittrichtung geschnittenen Kristalls war die Zweifachsymmetrie erkennbar und der Doppelbrechungsparameter ist ebenfalls sehr
55
stark vom Rotationswinkel abhängig. Die in [21] dargestellte Doppelbrechung erklärt demnach qualitativ die unterschiedlich langen Bereiche einer stabilen Polarisation der Beispiele dieser vorliegenden
Arbeit.
Abbildung 5.10: Maximum von g1,x1 · g2,x1 und g1,x2 · g2,x2 im Stabilitätsbereich der radialen Polarisation.
56
Abbildung 5.11: Maximum von g1,x1 · g2,x1 und g1,x2 · g2,x2 im Stabilitätsbereich der azimutalen Polarisation.
Abbildung 5.12: Resonatorlängendifferenzen der Stabilitätsbereiche, in denen nur die radiale oder
azimutale Polarisation stabil ist in Abhängigkeit von Schnittrichtung und Kristalldrehungen in mm.
57
5.8 Strahlradien des Modes 1. Ordnung der erzeugten
Polarisationen
Da der Grundmode in der Mitte des Querschnitts seine maximale Intensität hätte, das elektromagnetische Feld bei azimutaler oder radialer Polarisation aber in der Mitte null betragen muss (siehe Abschnitt 5.6), kann der Grundmode nicht anschwingen, und die Ausgangsenergie wird demnach vom
nächst höheren Mode, den Mode 1. Ordnung dominiert. In den Abbildungen 5.13 und 5.14 sind die
Strahlradien des Modes 1. Ordnung in der Mittelebene des Kristalls in x1 - und in x2 -Richtung im Stabilitätsbereich der radialen Polarisation dargestellt. Darin ist zu erkennen, dass die Strahlradien stark
vom Kristallschnitt und dem Rotationswinkel abhängen. Bei immer länger werdenden Resonatoren
nimmt der Strahlradius ab. Grund dafür ist diese Resonatorgeometrie, welche die ABCD-Matritzen,
siehe Abschnitt 3.5.2, und damit den gesamten Strahlengang im Resonator bestimmt. Beim [100]Schnitt mit beiden Rotationswinkel von Ψ = 0◦ und Ψ = 45◦ sind die Strahlradien am geringsten.
Mittelgroße Strahlradien treten beim [111]-Schnitt auf. Im Fall des in [110]-Richtung geschnittenen
Kristalls treten die größten Strahlradien auf, wobei dieser in x1 -Richtung bei einem Rotationswinkel
von Ψ = 0◦ und in x2 -Richtung bei Ψ = 90◦ am höchsten ist.
Die Strahlradien des Modes 1. Ordnung in der Mittelebene des Kristalls in x1 - und in x2 -Richtung im
Stabilitätsbereich der azimutalen Polarisation sind in den Abbildungen 5.15 und 5.16 dargestellt. Bei
diesem Polarisationszustand sind die Strahlradien für fast alle Kristallschnitte und -drehungen in ihren jeweiligen Stabilitätsbereichen ähnlich groß. In x1 -Richtung werden beim [110]-Schnitt mit einer
Rotation von Ψ = 90◦ kurz vor dem Instabilwerden des Resonators die Strahlradien sehr groß. In x2 Richtung ist dies beim [110]-Schnitt mit einer Rotation von Ψ = 0◦ der Fall.
Abbildung 5.13: Strahlradius des Modes 1. Ordnung in der Kristallmitte in x1 -Richtung im Stabilitätsbereich der radialen Polarisation in µm.
58
Abbildung 5.14: Strahlradius des Modes 1. Ordnung in der Kristallmitte in x2 -Richtung im Stabilitätsbereich der radialen Polarisation in µm.
Abbildung 5.15: Strahlradius des Modes 1. Ordnung in der Kristallmitte in x1 -Richtung im Stabilitätsbereich der azimutalen Polarisation in µm.
59
Abbildung 5.16: Strahlradius des Modes 1. Ordnung in der Kristallmitte in x2 -Richtung im Stabilitätsbereich der azimutalen Polarisation in µm.
60
5.9 Ausgangsleistungen der erzeugten
Polarisationen
In den Abbildungen 5.17 und 5.18 ist die Ausgangsleistung der Resonatoren im Falle der alleinigen
Stabilität des radialen bzw. azimutalen Polarisationszustandes dargestellt. Die Ausgangsleistungen
sind im Allgemeinen bei allen Schnittrichtungen und Rotationswinkeln ähnlich groß. Lediglich im
Fall des in [111]-Richtung geschnittenen Kristalls sind die Ausgangsleistungen geringer. Am Beginn
des Stabilitätsbereiches sind die Ausgangsleistungen 0W und steigen mit steigender Resonatorlänge
an. Bei ca. 25W Ausgangsleistung tritt im Fall der alleinigen radialen Polarisation bei allen Schnittrichtungen, außer der [111]-Richtung, die diese Leistung nicht erreicht, ein kleiner “Knick” auf.
Das heißt, dass trotz steigender Resonatorlänge die Ausgangsleistung kurzzeitig wieder abnimmt,
um dann bei weiter steigender Länge auf ca. 27W anzusteigen, bis der azimutale Polarisationszustand ebenfalls stabil wird. Dann wären beider Polarisationen theoretisch stabil und der tatsächlich
auftretende Polarisationszustand unbestimmt, siehe [30].
Im Fall der alleinigen stabilen azimutalen Polarisation werden beim [100]-Schnitt maximal ca. 21W ,
beim [111]-Schnitt ca. 13W und beim [110]-Schnitt ca. 25W Ausgangsleistung erzielt. Mit zunehmender Resonatorlänge sinken dann die Ausgangsleistungen bei fast allen Fällen auf ca. 4W ab,
ehe der Resonator instabil wird. Nur bei den Rotationswinkeln von Ψ = 0◦ und Ψ = 90◦ beim in
[110]-Richtung geschnittenen Kristall wird der Resonator schon bei Erreichen von ca. 11W Ausgangsleistung instabil.
Zusammenfassend ist in Abbildung 5.19 zu sehen, dass die Ausgangsleistung für fast alle Kristallschnitte und -rotationen bei alleiniger radialer Polarisation größer als bei alleiniger azimutaler Polarisation ist. Dies liegt an der besseren Verstärkung von mehr Moden niedriger Ordnung aufgrund
der geeigneteren Resonatorgeometrie. Da bei dieser Simulation jedoch keine Rückkopplung von
der berechneten Modenverteilung, welche stark von dem gaußförmigen Pumpprofil abweicht, zur
absorbierten Pumplichtverteilung erfolgt, haben die hier präsentierten Ergebnisse zur Ausgangsleistung nur begrenzte Aussagekraft. Eine iterative Berechnung würde hier genauere Ergebnisse liefern.
61
Abbildung 5.17: Ausgangsleistung im Stabilitätsbereich der radialen Polarisation in W .
Abbildung 5.18: Ausgangsleistung im Stabilitätsbereich der azimutalen Polarisation in W .
62
Abbildung 5.19: Maximale Ausgangsleistung im Stabilitätsbereich der radialen und azimutalen Polarisation in Abhängigkeit von Schnittrichtung und Kristalldrehungen in W .
63
5.10 Strahlqualität der erzeugten Polarisationen
Die Strahlqualität hängt von dem jeweiligen Anteil der Moden an der Ausgangsleistung ab, siehe u.a.
[27]. Eine Strahlqualität von 1.0 würde sich ergeben, wenn nur der Grundmode zur Ausgangsleistung
beitragen würde. Da aber wie bereits beschrieben dieser Grundmode hier nicht auftritt, ergibt sich
die beste Strahlqualität bei alleinigem Auftreten der Moden erster Ordnung mit einem Wert von 2.0,
siehe [44].
In Abbildung 5.20 sind die Strahlqualitäten in Abhängigkeit von der Resonatorlänge sowie den Kristallschnittrichtungen und -rotationswinkeln im Fall der alleinigen radialen Polarisation dargestellt.
Zu Beginn des Stabilitätsbereiches wird nur der Mode der ersten Ordnung verstärkt, und die Strahlqualität liegt bei allen Fällen bei 2.0. Dies korrespondiert mit einem großen Strahlradius dieser Mode und mit der Abwesenheit von Moden noch höherer Ordnung, siehe Abbildungen 5.13 und 5.14.
Mit länger werdendem Resonator werden die Strahlradien des Modes erste Ordnung aber geringer,
so dass bei konstant angenommenem Pumpprofil weitere Moden noch höherer Ordnung verstärkt
werden können. Eine Verschlechterung der Strahlqualität bis auf ca. 5.5 ist bei fast allen Schnittrichtungen die Folge. Nur im Fall des [111]-Schnitts verschlechtert sich die Strahlqualität aufgrund des
kurzen alleinigen Stabilitätsbereiches der radialen Polarisation nur auf etwa 3.5, wobei allerdings
auch die Ausgangsleistung geringer ist.
Die Strahlqualität im alleinigen azimutalen Fall ist in Abbildung 5.21 zu sehen. Mit länger werdendem Resonator steigt diese von minimal 8.1 (beim [110]-Schnitt mit einem Rotationswinkel von
Ψ = 45◦ ) bis auf maximal 9.8 an. Da diese Strahlqualität sehr schlecht ist und mehrere Sprünge
in ihrem Verlauf bei der Änderung der Resonatorlänge auftreten, ist anzunehmen, dass der Mode
erster Ordnung nur schwach gegenüber den Moden noch höherer Ordnung verstärkt wird. Eine niedrigere Ausgangsleistung bei der azimutalen gegenüber der radialen Polarisation, siehe Abbildung
5.19, bestätigt dies. Deshalb ist die Strahlqualität bei diesem Beispiel im alleinigen radialen Bereich geringer als im alleinigen azimutalen Stabilitätsbereich, siehe zusammenfassend in Abbildung
5.22.
64
Abbildung 5.20: Strahlqualität im Stabilitätsbereich der radialen Polarisation.
Abbildung 5.21: Strahlqualität im Stabilitätsbereich der azimutalen Polarisation.
65
Abbildung 5.22: Strahlqualität bei maximaler Ausgangsleistung im Stabilitätsbereich der radialen
und azimutalen Polarisation in Abhängigkeit von Schnittrichtung und Kristalldrehungen.
66
5.11 Zusammenfassung und Schlussfolgerung
In diesem Abschnitt wurde das Stabilitätsverhalten von einem Resonator mit einem Nd:YAG-Kristall
vollständig numerisch untersucht. Dabei soll eine reine azimutale bzw. eine rein radiale Polarisation
des Ausgangsstrahls ohne zusätzliche optische Elemente erreicht werden. Durch die spannungsinduzierte Doppelbrechung erfährt die Lichtwelle eines Polarisationszustandes einen anderen Brechungsindex als die Lichtwelle eines anderen, senkrecht darauf stehenden, Polarisationszustandes. Dadurch
kann bei einer Resonatorgeometrie der Strahlengang eines Polarisationszustandes im Resonator verbleiben, während der andere diesen verlässt. Damit ist nur ein Polarisationszustand stabil. Dazu wird
eine dreidimensionale Finite-Element-Analyse der Strukturmechanik zur Berechnung der Verteilung
des Brechungsindexes aus der Verteilung des absorbierten Pumplichtes durchgeführt. Die Ausgangsleistung und die Strahlqualität werden mit Hilfe der dynamischen Multimode Analyse berechnet. Variiert wird bei diesem Beispiel die Länge des Resonators. Dabei wird bei einem kurzen Resonator ein
rein radialer und bei einem langen Resoantor ein rein azimutaler Polarisationszustand erreicht. Die
Längen dieser Bereiche, in denen nur eine Polarisation stabil ist, hängt dabei stark vom Kristallschnitt
ab. Der Resonator mit dem in [111]-Richtung geschnittenen Kristall weist den kürzesten Längenbereich auf und im Falle des [110]-Schnittes den längsten. Die Rotationswinkel der Kristalle um ihre
eigene Längsachse haben dabei keinen großen Einfluss. Die Ausgangswerte, wie Ausgangsleistung
oder Strahlqualität, hängen sehr stark von den Geometriedaten des Resonators ab. Bei dem alleinigen
radialen Polarisationszustand werden höhere Ausgangsleistung und bessere Strahlqualitäten erreicht,
als bei dem alleinigen azimutalen Polarisationszustand. Es ließen sich wahrscheinlich auch Resonatorkonfigurationen finden, wo die Strahlqualität des alleinigen azimutalen Polarisationszustandes
den Bestwert von 2.0 erreicht. Genauere Ergebnisse ließen sich mit einer erneuten Berechnung der
absorbierten Wärmeverteilung aus den berechneten Eigenmoden erzielen.
67
68
6 Zusammenfassung und Ausblick
6.1 Zusammenfassung
In dieser Arbeit wird der Einfluss der spannungsinduzierten Doppelbrechung in Laserkristallen auf
das Verhalten von Laserresonatoren untersucht. Es wird mit numerischen Methoden an zwei Beispielenresonatoren mit Nd:YAG-Kristallen analysiert, wie der photoelastische Effekt das Polarisationsverhalten des Resonators in Abhängigkeit von Kristallschnittrichtung und -drehung beeinflusst. Die
Berechnung der Strukturmechanik wird mit einer vollen dreidimensionalen Finite-Elemente-Analyse
und die Berechnung der Eigenpolarisationszustände mit einer zweidimensionalen Jonesmatrixanalyse durchgeführt.
Im Kapitel 2 sind die verschiedenen Kristallsysteme dargestellt und der Einfluss derer innerer Symmetrien auf die physikalischen Effekte im Kristall kurz erläutert. Es werden die Grundlagen der thermischmechanischen und der optomechanischen Kopplung im Laserkristall dargestellt. Ausgehend
davon werden die Auswirkungen des photoelastischen Effektes auf die Brechungsindizes infolge
thermischer und mechanischer Felder betrachtet.
Dessen Einfluss auf den Eigenpolarisationszustand wird im Kapitel 3 erläutert. Diese Zustände werden mit Hilfe des Jonesformalismus berechnet. Zusätzlich zur spannungsinduzierten Doppelbrechung können aber auch weitere optische Elemente wie Brewsterplatten den Eigenpolarisationszustand beeinflussen. Die Eigenpolarisationszustände verändern die Verlustfaktoren der Eigenmoden im Resonator, welche in die Dynamische Multimode Analyse einfließen, siehe [27]. Mit dieser
werden die Ausgangsleistung und die Strahlqualität des Resonators berechnet. Auch wird der Einfluss der spannungsinduzierten Doppelbrechung auf das Stabilitätsverhalten eines Laserresonators
beschrieben.
Eine Ausgangsleistungssteigerung und Verbesserung der Strahlqualität mittels Einbau zweier Glasplatten im Brewsterwinkel wird im ersten Beispiel, Kapitel 4, numerisch untersucht. Ausgehend von
der Pumpkonfiguration werden der Temperaturverlauf, sowie die mechanischen Spannungen und
Dehnungen berechnet. Es zeigt sich, dass die resultierende räumliche Verteilung der Doppelbrechung sehr stark vom Kristallschnitt und dessen Drehung um die eigene Längsachse abhängt. Dabei
werden der [100]-Schnitt (Drehung um 0◦ und 90◦ ), der [110]-Schnitt (Drehung um 0◦ , 45◦ und 90◦ )
und der [111]-Schnitt (ohne Variation des Drehwinkels) untersucht. Es werden die unbestimmten
Eigenpolarisationszustände in einem Resonator ohne Brewsterplatten gezeigt. In einem Resonator
mit zwei Brewsterplatten stellt sich dagegen ein bestimmter Eigenpolarisationszustand ein. Es wird
an diesem numerischen Beispiel nachgewiesen, dass unterschiedliche Kristallschnittrichtungen und
-drehungen einen erheblichen Einfluss auf die Ausgangsleistung, die Strahlqualität und die Polarisationsreinheit des Ausgangsstrahls des Resonators haben.
Am zweiten Beispiel, Kapitel 5 wird die unterschiedliche Stabilität von azimutaler und radialer Polarisation aufgrund spannungsinduzierter Doppelbrechung genutzt, um den gesamten Resonator nur
für eine der beiden Polarisationen ohne zusätzliche optische Baulelemente stabil zu betreiben. Nach
69
der Darstellung der berechneten Temperatur-, Spannungs- und Dehnungsverteilung wird ebenfalls
gezeigt, dass das entstehende Doppelbrechungsmuster wesentlich vom Kristallschnitt abhängt. Die
Kristallschnitte und -drehungen werden wie im vorhergehenden Beispiel variiert. Nach der Darstellung der resultierenden Laguerre-Moden-Profile wird gezeigt, dass bei bestimmten Resonatorlängen
nur der radiale oder der azimutale Eigenpolarisationszustand stabil ist. Diese Längenbereiche sind
sehr stark abhängig vom Kristallschnitt und -drehung. In Abhängigkeit von diesen werden die Strahlradien erster Ordnung, die Ausgangsleistungen und die Strahlqualität berechnet.
Es wird in beiden Beispielen gezeigt, dass sich durch geeignete Wahl der Resonatorgeometrie, sowie
des Kristallschnitts und -drehung die resultierende Ausgangsleistung, die Strahlqualität und die Polarisationsreinheit bei einem gewünschten Eigenpolarisationszustand optimieren lassen. Der bisher
am häufigsten verwendete Laserkristall mit einem [111]-Schnitt muss dabei nicht immer die besten
Ergebnisse ausweisen. Unter Ausnutzung der inneren Symmetrie des Kristalls lassen sich mit anderen Schnitt-richtungen oft bessere Ergebnisse erzielen. Da Experimente dazu sehr kostenintensiv
sind, lassen sich mit den hier präsentierten numerischen Methoden neue Laserresonatoren sehr viel
schneller und kostengünstiger entwickeln.
6.2 Einschränkungen
Große Aufmerksamkeit eines Ingenieurs genießt immer die Wahl der mechanischen Randbedingungen. In dem benutzten Programm ALSD ist momentan nur die Auswahl zwischen fester Einspannung und völliger Bewegungsfreiheit der Kristallflächen möglich, siehe Abschnitt 2.4.3. Die resultierenden unterschiedlichen Spannungsverläufe im Kristall bedingen aber sehr unterschiedliche
spannungsinduzierte Doppelbrechungsmuster. Die Ergebnisse beider Annahmen weichen demnach
erheblich voneinander ab. Um genauere Ergebnisse zu erzielen, müssten die Einspannkonstruktionen
des Laserkristalls, inklusive deren thermischen Randbedingungen, mit simuliert werden. Da YAG mit
einem E-Modul von E = 2, 775 · 105 N/mm2 , siehe Kapitel 4, gegenüber einer Einspannung aus Kupfer (E = 1, 3 · 105 N/mm2 ) oder Aluminium (E = 7 · 104 N/mm2 ) aber sehr steif ist, ist eher von einer
völligen Bewegungsfreiheit der Kristallflächen als von einer starren Einspannung auszugehen.
In [60] wurde gezeigt, dass die mechanischen Materialparameter Ci jkl nur schwach von der Temperatur abhängen, wogegen die thermische Leifähigkeit k und der thermische Ausdehnungskoeffizient
α stark von der Temperatur abhängig sind, siehe Abschnitt 2.4.2. Diese thermischen Abhängigkeiten
werden in dieser Arbeit vernachlässigt. Ebenso wird die Abhängigkeit der Änderung des Brechungs0
indexes aufgrund der Temperaturänderung dn
dT von der Temperatur an sich nicht berücksichtigt, siehe
[61].
In den hier verwendeten Modellen wird die Temperaturverteilung in den Kristallen nur aufgrund der
Pumplichtverteilung im kalten“Kristall berechnet. Der Einfluss der veränderten Brechungsindizes
”
im warmen“Kristall auf diese Pumplichtverteilung wird hier vernachlässigt. Für eine genauere Be”
rechnung der Eigenpolarisationszustände, Ausgangsleistungen, etc., müsste nach der Bestimmung
der Modenverteilung eine erneute Berechnung der Brechungsindizes aufgrund des veränderten Absorptionsverteilung des Pumplichtes stattfinden.
70
6.3 Ausblick
Die hier präsentierten Ergebnisse wurden mit numerischen Simulationen berechnet. Experimente zur
Validierung dieser Simulationsergebnisse sollten demnächst durchgeführt werden.
In dieser Arbeit wurde an zwei Beispielen ein Kristall aus YAG behandelt, der dem kubischen Kristallsystem und der Kristallklasse m3m angehört. Diese Kristallklasse weist keine Kopplungen zwischen elektrischen und magnetischen Feldern auf, siehe Abschnitt 2.4.2. Elektrooptische Effekte,
wie der Pockelseffekt, siehe Abschnitt 2.4.3, können in fortführenden Arbeiten mit einbezogen werden, wie es z.B. in [34] mit analytischen Berechnungsmethoden geschehen ist. Des Weiteren sind
die Wärmeausdehnung und -leitfähigkeit, sowie die Brechungsindizes in diesem kubischen Kristallsystem im unbelasteten Zustand isotrop. In fortführenden Arbeiten könnten solche Effekte in
Laserkristallen anderer Kristallklassen, die solche Kopplungen oder Anisotropien besitzen, ebenfalls
berücksichtigt werden. Eine Schwierigkeit könnte aber dabei sein, dass die dabei auftretenden Effekte quantitativ geringer sind, als die Modellierungs- und Messungenauigkeiten bei dessen Simulation
bzw. experimenteller Validierung.
Die mechanischen Randbedingungen, siehe Abschnitt 2.4.3, können im jetzigen Programmcode in
allen Richtungen entweder komplett starr oder komplett freibeweglich angenommen werden. In realen Festkörperlasern ist der Kristall aber z.B. mit einer Graphithülle umgeben und zur besseren
Wärmeabfuhr in einem Kupferblock gespannt. Dabei ist radialer Richtung weder von einer festen
Einspannung noch von der Möglichkeit einer freien Verschiebung, sondern eher von einer “Auflagersteifigkeit” auszugehen. Diese aber experimentell oder numerisch zu bestimmen, dürfte aber sehr
aufwändig sein. Des Weiteren ist in longitudinaler Richtung davon auszugehen, dass in diesem Fall
an der Kristallmantelfläche keine Einspannung, sondern ein geringer Reibwiderstand herrscht. Dies
könnte in zukünftigen Arbeiten durch geeignete mechanische Modelle mit berücksichtigt werden.
Zur Kompensation der Doppelbrechung werden in der Praxis zum Beispiel in dem Resonator zwei
Verstärkerkristalle und zwischen diesen beiden ein 90· -Quarzrotator eingebaut, siehe [62]. Dies
könnte in zukünftigen Arbeiten mit den hier verwendeten Methoden genauer simuliert und der entstehende Ausgangsstrahl hinsichtlich Strahlqualität, Ausgangsleistung, etc. untersucht werden.
Des Weiteren können auch die polarisationsändernden Wirkungen eines Verstärkerkristalls außerhalb des Resonators mit dem Jonesformalismus berechnet werden.
Die spannungsinduzierte Doppelbrechung in einem Laserkristall oder einem Verstärkerkristall kann
auch als Ausgangspunkt für eine Berechnung der elektromagnetischen Welle mittels einer vektoriellen “Beam-propagation-methode” dienen, siehe [63].
71
72
Abbildungsverzeichnis
2.1
2.3
Koordinatensystem im kubischen Gitter (a) in [100]-Schnittrichtung und (b) in [111]Schnittrichtung. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Übersicht über physikalische Effekte im Kristall durch Heckmann Diagramm, angelehnt an [8, 9]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Indicatrix, [18] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.1
3.2
3.3
3.4
Definitionen des Polarkoordinatenwinkels ψ und des Polarisationswinkels ϕ, [18] . .
Schwingungsrichtung des elektrischen Feldes bei radialer und azimutaler Polarisation
Stabiltätsdigramm eines passiven Resonators, angelehnt an [1] . . . . . . . . . . . .
Stabiler und instabiler Resonator, [18] . . . . . . . . . . . . . . . . . . . . . . . . .
2.2
Laserresonator mit Endspiegel (HR), Auskoppelspiegel (OC) und dem Nd:YAGKristall. Dieser ist seitgepumpt. Die zwei Brewsterplatten (PB) befinden sich zwischen dem HR und dem Kristall, siehe [47]. . . . . . . . . . . . . . . . . . . . . . .
4.2 (a) Zweidimensionales Gitter für den Jonesformalismus und (b) dreidimensionales
Finite-Elemente-Gitter, siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Temperaturverlauf im seitgepumpten Kristall in K . . . . . . . . . . . . . . . . . . .
4.4 Ausgewählte mechanische Spannungen σ im Laserkristall bei 75W Pumpleistung in
N/mm2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5 Von Mises-Vergleichsspannung σMises im Laserkristall bei 75W Pumpleistung in
N/mm2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6 Räumliche Verteilung der Doppelbrechung ∆n in der x1 -x2 -Ebene im Laserkristall,
siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7 Ausgewählte Realteile der Eigenwerte der Jonesmatrizen, welche zur azimutalen Eigenpolarisation des übertragenden Feldes bei 75W Pumpleistung im Resonator ohne
Brewsterplatten gehören, siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . .
4.8 Realteile der beiden Eigenvektoren der Jonesmatrizen bei einer [100]-Schnittrichtung
und Ψ = 0◦ mit 75W Pumpleistung im Resonator ohne Brewsterplatten. Diese Eigenpolarisationszustände gehören zu Abbildung 4.7(a), siehe [47]. . . . . . . . . . . . .
4.9 Betrag der Eigenwerte der Jonesmatrizen bei 15W Pumpleistung bei verschiedenen
Schnittrichtungen und Rotationswinkeln Ψ in Resonatoren mit Brewsterplatten. Die
lokal am höchsten auftretenden Werte entsprechen dem Transmissionsfaktor für die
DMA, siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.10 Betrag der Eigenwerte der Jonesmatrizen bei 75W Pumpleistung bei verschiedenen
Schnittrichtungen und Rotationswinkeln Ψ in Resonatoren mit Brewsterplatten. Die
lokal am höchsten auftretenden Werte entsprechen dem Transmissionsfaktor für die
DMA, siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
23
24
26
4.1
29
30
31
32
32
33
34
35
36
37
73
4.11 Übertragene Eigenvektoren der Jonesmatrizen bei 15W Pumpleistung für unterschiedliche Schnittrichtungen und Rotationswinkel Ψ im Resonator mit Brewsterplatten,
siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.12 Übertragene Eigenvektoren der Jonesmatrizen bei 75W Pumpleistung für unterschiedliche Schnittrichtungen und Rotationswinkel Ψ im Resonator mit Brewsterplatten,
siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.13 Gewichteter Abweichungswinkel αdevia (nach Gleichung (3.21)) der Polarisation im
Vergleich zu einem linear polarisierten Strahl entlang der x1 -Achse in Abhängigkeit
von der Pumpleistung in Resonatoren mit Brewsterplatten, siehe [47]. . . . . . . . .
4.14 Ausgangsleistung der Resonatoren mit und ohne Brewsterplatten in Abhängigkeit
von der Pumpleistung, siehe [47]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.15 Strahlqualität des Ausgangsstrahls in x1 -Richtung der Resonatoren mit und ohne
Brewsterplatten in Abhängigkeit von der Pumpleistung, siehe [47]. . . . . . . . . . .
4.16 Strahlqualität des Ausgangsstrahls in x2 -Richtung der Resonatoren mit und ohne
Brewsterplatten in Abhängigkeit von der Pumpleistung, siehe [47]. . . . . . . . . . .
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.14
5.15
5.16
5.17
5.18
74
Laserresonator mit Endspiegel (HR), Auskoppelspiegel (OC), und dem Nd:YAG Kristall. Der Kristall ist seitgepumpt. Die Abstände zwischen dem HR und dem Kristall
bzw. zwischen dem OC und dem Kristall sind immer gleich groß. . . . . . . . . . .
(a) Draufsicht des Gitters und (b) perspektivische Ansicht des Gitters. . . . . . . . .
Temperaturverlauf im Laserkristall in K. . . . . . . . . . . . . . . . . . . . . . . . .
Mechanische von Mises-Vergleichsspannungen im Laserkristall in N/mm2 . . . . . .
Brechungsindexänderung ∆ntherm im Laserkristall aufgrund des thermischen Feldes. .
Brechungsindexänderung ∆nmech im Laserkristall aufgrund des mechanischen Feldes.
Gesamter Brechungsindex im Kristall aufgrund der thermischen und mechanischen
Felder. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Doppelbrechung des Laserkristalls in Abhängigkeit von den einzelnen Schnittrichtung und Kristalldrehungen. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Muster ausgewählter Laguerre-Moden im Laserkristall. . . . . . . . . . . . . . . . .
Maximum von g1,x1 ·g2,x1 und g1,x2 ·g2,x2 im Stabilitätsbereich der radialen Polarisation.
Maximum von g1,x1 · g2,x1 und g1,x2 · g2,x2 im Stabilitätsbereich der azimutalen Polarisation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Resonatorlängendifferenzen der Stabilitätsbereiche, in denen nur die radiale oder
azimutale Polarisation stabil ist in Abhängigkeit von Schnittrichtung und Kristalldrehungen in mm. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Strahlradius des Modes 1. Ordnung in der Kristallmitte in x1 -Richtung im Stabilitätsbereich der radialen Polarisation in µm. . . . . . . . . . . . . . . . . . . . . . . . .
Strahlradius des Modes 1. Ordnung in der Kristallmitte in x2 -Richtung im Stabilitätsbereich der radialen Polarisation in µm. . . . . . . . . . . . . . . . . . . . . . . . .
Strahlradius des Modes 1. Ordnung in der Kristallmitte in x1 -Richtung im Stabilitätsbereich der azimutalen Polarisation in µm. . . . . . . . . . . . . . . . . . . . . . . .
Strahlradius des Modes 1. Ordnung in der Kristallmitte in x2 -Richtung im Stabilitätsbereich der azimutalen Polarisation in µm. . . . . . . . . . . . . . . . . . . . . . . .
Ausgangsleistung im Stabilitätsbereich der radialen Polarisation in W . . . . . . . . .
Ausgangsleistung im Stabilitätsbereich der azimutalen Polarisation in W . . . . . . .
38
39
41
41
42
42
47
47
48
49
50
51
51
53
54
56
57
57
58
59
59
60
62
62
5.19 Maximale Ausgangsleistung im Stabilitätsbereich der radialen und azimutalen Polarisation in Abhängigkeit von Schnittrichtung und Kristalldrehungen in W . . . . . . .
5.20 Strahlqualität im Stabilitätsbereich der radialen Polarisation. . . . . . . . . . . . . .
5.21 Strahlqualität im Stabilitätsbereich der azimutalen Polarisation. . . . . . . . . . . . .
5.22 Strahlqualität bei maximaler Ausgangsleistung im Stabilitätsbereich der radialen und
azimutalen Polarisation in Abhängigkeit von Schnittrichtung und Kristalldrehungen.
63
65
65
66
75
76
Literaturverzeichnis
[1] W. Koechner. Solid-State Laser Engineering. Springer, 1999.
[2] J. F. Shackelford. Werkstofftechnologie für Ingenieure. Pearson Studium, München, 2005.
[3] I. Shoji, T. Taira, and A. Ikesue. Thermally-induced-birefringence effects of highly Nd3 + -doped
Y3 Al5 O12 ceramic lasers. Optical Materials, 29, 2007.
[4] E. A. Khazanov. Thermally induced birefringence in Nd:YAG ceramics. Optics Letters, 27(9),
May 2002.
[5] E. Asselborn, P. J. Chiappero, J. Galvier, and H. Chaumeton. Kleine Enzyklopädie der Mineralien. Tandem Verlag GmbH, Köln, 2005.
[6] http://www.mineralienatlas.de.
[7] I. Kleber, H. J. Bautsch, and J. Bohm. Einführung in die Kristallographie. Verlag Technik
GmbH, Berlin, 1990.
[8] J. F. Nye. Physical Properties of Crystals. Clarendon Press, Oxford, 1985.
[9] R. E. Newnham. Properties of materials - anisotropy, symmetry, structure. University Press,
Oxford, 2005.
[10] http://www.toplent.com.
[11] K. Jänich. Lineare Algebra. Springer-Verlag Berlin Heidelberg New York, 2000.
[12] M. Wohlmuth. Modeling and simulation of solid-state laser resonators using a Dynamic Multimode Analysis (DMA). PhD thesis, Institut für Informatik, Friedrich-Alexander Universität
Erlangen-Nürnberg, Nürnberg, Germany, 2011.
[13] S. Timoshenko and J. N. Goodier. Theory of Elasticity. McGraw-Hill, New York, 1951.
[14] Y. Lumer, I. Moshe, S. Jackel, Z. Horvitz, A. Meir, R. Feldmann, and Y. Shimony. Depolarization induced by pump edge effects in high average power laser rods. J. Opt. Soc. Am. B, 27(1),
January 2010.
[15] W. Voigt. Lehrbuch der Kristallphysik. Teubner, Leipzig und Berlin, 1910.
[16] K. B. Doyle, V. L. Genberg, and G. J. Michels. Integrated Optomechanichal Analysis - second
edition. SPIE Press, Bellingham, Washington, 2012.
[17] B. E. A. Saleh and M. C. Teich. Fundamentals of Photonics, 2nd edition. Wiley, Hoboken,
New Jersey, 2007.
77
[18] T. Graupeter and C. Pflaum. Stability analysis of solid-state lasers regarding thermal lensing
effect. volume 8433. SPIE Photonics Europe, of Proc. SPIE Photonics Europe, Laser Sources
and Applications, May 2012.
[19] R. Hua, S. Wada, and H. Tashiro. Principles and limitations of a quater-wave plate for reducing the depolarization loss from thermally induced birefringence in Nd:YAG lasers. Optics
Communications, 175, February 2000.
[20] W. Koechner and D. K. Rice. Effect of birefringence on the performance of linearly polarized
Nd:YAG lasers. IEEE Journal of Quantum Electronics, QE-6(9), September 1970.
[21] W. Koechner and D. K. Rice. Birefringence of YAG:Nd laser rods as a function of growth
direction. J. Opt. Soc. Am., 61(6), June 1971.
[22] Y. Chen, B. Chen, M. K. R. Patel, and M. Bass. Calculation of thermal-gradient-induced stress
birefringence in slab lasers-I. IEEE Journal of Quantum Electronics, 40(7), July 2004.
[23] Q. Lü, U. Wittrock, and S. Dong. Photoelastic effects in Nd:YAG rod and slab lasers. Optics
and Laser Technology, 27(2), 1995.
[24] Y. Kitamura, N. Miyazaki, T. Mabuchi, and T. Nawata. Birefringence simulation of annealed
ingot of magnesium fluoride single crystal. Journal of Crystal Growth, 311, 2009.
[25] H. Ogino, N. Miyazaki, T. Mabuchi, and T. Nawata. Birefringence simulation of annealed ingot
of calcium fluoride single crystal. Journal of Crystal Growth, 310, 2007.
[26] R. W. Dixon. Photoelastic properties of selected materials and their relevance for applications
to acoustic light modulators and scanners. J. Appl. Phys., 38(13), 1967.
[27] M. Wohlmuth, C. Pflaum, K. Altmann, M. Paster, and C. Hahn. Dynamic multimode analysis
of Q-switched solid state laser cavities. Optics Express, 17(20), September 2009.
[28] E. Collett. Field Guide to Polarization. SPIE Press, Bellingham, Washington, 2005.
[29] R. C. Jones. A new calculus for the treatment of optical systems. J. Opt. Soc. Am., 31, July
1941.
[30] N. Hodgson and H. Weber. Laser Resonators and Beam Propagation. Springer, New York,
2005.
[31] A. V. Nesterov and V. G. Niziev. Laser beams with axial symmetric polarization. J. Phys. D:
Appl. Phys., 33, 2000.
[32] D. Pohl. Operation of a ruby laser in the purely transverse electric mode TE01 . Appl. Phys.
Lett., 20(7), April 1972.
[33] S. N. Savenkov, O. I. Sydoruk, and R. S. Muttiah. Eigenanalysis of dichroic, birefringent, and
degenerate polarization elements: a Jones-calculus study. Applied Optics, 46(27), September
2007.
[34] J. Junghans, M. Keller, and H. Weber. Laser resonators with polarizing elements - eigenstates
and eigenvalues of polarization. Applied Optics, 13(12), Dezember 1974.
78
[35] A. J. Kemp, G. J. Friel, T. K. Lake, R. S. Conroy, and B. D. Sinclair. Polarization effects,
birefringent filtering, and single-frequency operation in laser containing a birefringent gain
crystal. IEEE Journal of Quantum Electronics, 36(2), February 2000.
[36] J. P. Taché. Intracavity skew-brewster-angle plates as a calibrated attenuator for gas lasers. .
Phys. D: Appl. Phys., 19, 1986.
[37] Y. Lumer, I. Moshe, Z. Horvitz, S. Jackel, G. Machavariani, and A. Meir. Thermally induced
birefringence in nonsymmetrically pumped laser rods and its implications for attainment of
good beam quality in high-power, radially polarized lasers. Applied Optics, 47(21), July 2008.
[38] ADVANCED SOFTWARE LASER DESIGN (ASLD) GMBH.
[39] J. M. Egglestone, T. J. Kane, K. Kuhn, J. Unternahrer, and R. L. Byer. The slab geometry
laser-part I: Theory. IEEE Journal of Quantum Electronics, 20(3), March 1984.
[40] C. C. Davis. Lasers and Electro-Optics. Cambridge Univ. Press, Cambridge, 1996.
[41] A. E. Siegman. Lasers. University Science Books, Mill Valley, 1986.
[42] H. Kogelnik and T. Li. Laser beams and resonators. Applied Optics, 5(10), October 1966.
[43] K. Yonezawa, Y. Kozawa, and S. Sato. Generation of a radially polarized laser beam by use of
the birefringence of a c-cut Nd:YVO4 . Optics Letters, 31(14), July 2006.
[44] I. Moshe, S. Jackel, and A. Meir. Production of radially or azimuthally polarized beams in
solid-state lasers and the elimination of thermally induced birefringence effects. Optics Letters,
28(10), May 2003.
[45] A. Ito, Y. Kozawa, and S. Sato. Selective oscillation of radially and azimuthally polarized laser
beam induced by thermal birefringence and lensing. J. Opt. Soc. Am. B, 26(4), April 2009.
[46] S. C. Tidwell, D. H. Ford, and W. D. Kimura. Generating radially polarized beams interferometrically. Applied Optics, 29(15), May 1990.
[47] T. Graupeter, R. Hartmann, and C. Pflaum. Calculations of eigenpolarisation in Nd:YAG laser
rods due to thermally induced birefringence. IEEE Journal of Quantum Electronics, 50(12),
December 2014.
[48] Q. Lü and H. Weber. Beam quality degradation of polarized, circularly symmetric beams caused
by a birefringent Nd:YAG rod. Optics Communications, 118, August 1995.
[49] I. Shoji and T. Taira. Intrinsic reduction of the depolarization loss in solid state lasers by use of
a (110)-cut Y3 Al5 O12 crystal. Appl. Phys. Lett., 80(17), April 2002.
[50] I. B. Mukhin, E. A. O. V. Palashov, Khazanov, I. A., and Ivanov. Influence of the orientation of a
crystal on thermal polarization effects in high-power solid-state lasers. Journal of Experimental
and Theoretical Physics Letters, 81(3), 2005.
[51] O. Puncken, H. Tünnermann, J. J. Morehead, P. Weßels, M. Frede, J. Neumann, and D. Kracht.
Intrinsic reduction of the depolarization in nd:yag crystals. Optics Express, 18(19), 2010.
[52] Y. Chen, B. Chen, M. K. R. Patel, and M. Bass. Calculation of thermal-gradient-induced stress
birefringence in slab lasers-I. IEEE Journal of Quantum Electronics, 40(7), July 2004.
79
[53] H. Göldner. Lehrbuch höhere Festigkeitslehre Band 2. Fachbuchverlag Leipzig Köln, 1992.
[54] K. E. Shafer, D. E. Eakins, D. F. Bahr, M. G. Norton, and K. G. Lynn. Strength enhancement
of single crystal laser components. J. Mater. Res., 18(11), November 2003.
[55] P. Muys, T. Moser, and T. Feurer. Polarization eigenstates of an axially symmetric laser beam
in a c-cut uniaxial crystal. J. Opt. Soc. Am. B, 24(10), October 2007.
[56] T. Moser, M. A. Ahmed, F. Pigeon, O. Parriaux, E. Wyss, and T. Graf. Generation of radially
polarized beams in Nd:YAG lasers with polarization selective mirrors. Laser Phys. Lett., 1(5),
April 2004.
[57] G. Machavariani, Y. Lumer, I. Moshe, A. Meir, S. Jackel, and N. Davidson. Birefringenceinduced bifocusing for selection of radially or azimuthally polarized laser modes. Applied
Optics, 46(16), June 2007.
[58] W. Koechner. Thermal lensing in a Nd:YAG laser rods. Applied Optics, 9(11), November 1970.
[59] M. S. Roth, E. W. Wyss, H. Glur, and H. P. Weber. Generation of radially polarized beams in a
Nd:YAG laser with self-adaptive overcompensation of the thermal lens. Optics Letters, 30(13),
July 2005.
[60] D. C. Brown. Nonlinear thermal distortion in YAG rod amplifiers. IEEE Journal of Quantum
Electronics, 34(12), December 1998.
[61] A. M. Bonnefois, M. Gilbert, P.-Y. Thro, and J.-M. Weulersse. Thermal lensing and spherical
aberration in high-power transversally pumped laser rods. Optics Communications, 259, 2006.
[62] Q. Lü, N. Kugler, H. Weber, S. Dong, N. Müller, and U. Wittrock. A novel approach for
compensation of birefringence in cylindrical Nd:YAG rods. Optical and Quantum Electronics,
28, 1996.
[63] R. Hartmann, T. Graupeter, and C. Pflaum. Analysis of birefringence effects in laser crystals
by full vectorial beam propagation method. volume 9131. of Proc. SPIE Photonics Europe,
Optical Modelling and Design III, April 2014.
80