wissen - Wiwi Uni

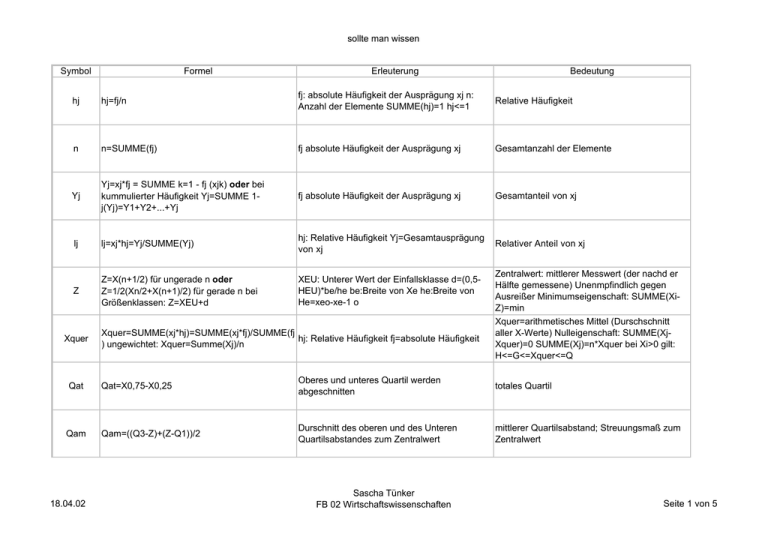
sollte man wissen
Symbol
Formel
Erleuterung
Bedeutung
hj
hj=fj/n
fj: absolute Häufigkeit der Ausprägung xj n:
Anzahl der Elemente SUMME(hj)=1 hj<=1
Relative Häufigkeit
n
n=SUMME(fj)
fj absolute Häufigkeit der Ausprägung xj
Gesamtanzahl der Elemente
Yj
Yj=xj*fj = SUMME k=1 - fj (xjk) oder bei
kummulierter Häufigkeit Yj=SUMME 1j(Yj)=Y1+Y2+...+Yj
fj absolute Häufigkeit der Ausprägung xj
Gesamtanteil von xj
lj
lj=xj*hj=Yj/SUMME(Yj)
hj: Relative Häufigkeit Yj=Gesamtausprägung
von xj
Relativer Anteil von xj
Z
Z=X(n+1/2) für ungerade n oder
Z=1/2(Xn/2+X(n+1)/2) für gerade n bei
Größenklassen: Z=XEU+d
XEU: Unterer Wert der Einfallsklasse d=(0,5HEU)*be/he be:Breite von Xe he:Breite von
He=xeo-xe-1 o
Xquer
Xquer=SUMME(xj*hj)=SUMME(xj*fj)/SUMME(fj
hj: Relative Häufigkeit fj=absolute Häufigkeit
) ungewichtet: Xquer=Summe(Xj)/n
Zentralwert: mittlerer Messwert (der nachd er
Hälfte gemessene) Unenmpfindlich gegen
Ausreißer Minimumseigenschaft: SUMME(XiZ)=min
Xquer=arithmetisches Mittel (Durschschnitt
aller X-Werte) Nulleigenschaft: SUMME(XjXquer)=0 SUMME(Xj)=n*Xquer bei Xi>0 gilt:
H<=G<=Xquer<=Q
Qat
Qat=X0,75-X0,25
Oberes und unteres Quartil werden
abgeschnitten
totales Quartil
Qam
Qam=((Q3-Z)+(Z-Q1))/2
Durschnitt des oberen und des Unteren
Quartilsabstandes zum Zentralwert
mittlerer Quartilsabstand; Streuungsmaß zum
Zentralwert
18.04.02
Sascha Tünker
FB 02 Wirtschaftswissenschaften
Seite 1 von 5
sollte man wissen
Var
Var=SUMME(Xi-Xquer)²/n= SUMME(XiXquer)²*fi/SUMME(fi)= SUMME(Xi²)/n-Xquer²
Streuungsmaß zum arithmetischen Mittel
Varianz: quadrat der Abweichungen von
arithmetischen Mittel
Ox
Ox=WURZEL(Var)=WURZEL(SUMME(XiXquer)²/n)
Streuungsmaß zum arithmetischen Mittel
Standardabweichung; Betrag der
Abweichungen von arithm. Mittel
ox²
ox²=SUMMEjm(oj²*fj)/SUMMEjm(fj)
+SUMME(Xjquer-Xquer)²*fj/SUMMEjm(fj)
oj²=Xjk-Xquer=(Xjk-Xjquer)+(Xjquer-Xquer)
Varianz=Varianz innerhalb der Gruppe+Varianz Streuungszerlegung (Varianzzerlegung)
zwischen den Gruppen
sx
sx=SUMME|X-Xquer|/n
Summe der Einzelabweichungen
mittlere absolute Abweichung
Cov(X,Y)=(SUMME(Xi-Xquer)(Yi-Yquer))/n=
SUMME(Xi*Yi)/n-Xquer*Yquer
Erkärt die Varianz von abhängign Variablen
(erklärende und erklärte Variable)
Kovarianz von X und Y
Cov(X,Y)
b
b=SUMME(Yi*ti*)/SUMME(ti*)²=(SUMME(Xi**Y
i))/SUMME(Xi*)²=Cov(X,Y)/Var(X) bei zwei
ti*=ti-tquer Xi*=Xi-Xiquer Bei zwei
Fequenzreihen:
Frequenzreihen: Yjquer=SUMMEk=1fj(Yjk)/fj
b=(SUMME(xj**Yquerj*fj))/SUMME(xj*²*fj)
Steigung der Trendgeraden
a
a=Yquer-b*tquer
Yi' sind die Punkte auf der Trendgerade
Funktion der Trendgerade
W(A)=g/m=R/N
g= günstige Fälle m=mögliche Fälle
R=günstige Ereignisse N=Gesamte Ereignisse Wahrscheinlichkeit des Eintreffens von A nach
W(A)=1 bei sicheren Ereignissen; W(A)=0 bei Laplace
unmöglichen Ereignissen
W(A)
18.04.02
Sascha Tünker
FB 02 Wirtschaftswissenschaften
Seite 2 von 5
sollte man wissen
W(Aquer) W(Aquer)=(m-g)/m=(N-R)/N=1-R/N=1-W(A)
g= günstige Fälle m=mögliche Fälle
R=günstige Ereignisse N=Gesamte Ereignisse Wahrscheinlichkeit des Nicht-Eintreffens von A
W(Aquer)=0 bei sicheren Ereignissen;
nach Laplace
W(Aquer)=1 bei Unmöglichen
W
W(A1uA2)=W(A1)+W(A2)-W(A1nA2)
(A1uA2)
Addition von Wahrscheinlichkeiten: Bei
einander gegenseitig paarweise
ausschließenden Ereignissen
W(A1uA2uA3)=W(A1)+W(A2)+W(A3)W (A1
[W(A1nA2)+W(A1nA3)+W(A2nA3)]+
uA2uA3)
W(A1nA2nA3)
Addition von Wahrscheinlichkeiten: Bei
einander gegenseitig paarweise
ausschließenden Ereignissen
W(A1nA2
n...nAn)
Multiplikation von Wahrscheinlichkeiten: Bei
stochastisch unverbundenen Ereignissen, wenn
beide eintreten sollen
W(A1nA2 n...nAn)=W(A1)*W(A2)*...*W(An)
W
W(A2|A1): durch A1 bedingte
W(A1nA2
(A1nA2)=W(A1)*W(A2|A1)*...*W(AN|A1n...nAnWahrscheinlichkeit von A2
n...nAn)
1)
Multiplikation bei stochastisch verbundenen
Ereignissen
W(A2|A1)
W(A2|A1)=W(A1nA2)/W(A1)
durch A1 bedingte Wahrscheinlichkeit A2
W(Ai|B)
W(Ai|B)=(W(B|Ai)*W(Ai))/
Summe(W(B|Ai)*W(Ai)
n über r
18.04.02
n über r=n!/(r!*(n-r)!)
W(Ai|B)=W(BnAi)/W(B)
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente
Sascha Tünker
FB 02 Wirtschaftswissenschaften
Wahrscheinlichkeit von B in Abhängigkeit von
disjunkten Wahrscheinlichkeiten Ai nach Bayes
Permutation mit Wiederholung: Anzahl der
vorhandenen Möglichkeiten bei statistisch
unverbundenen Ziehungen
Seite 3 von 5
sollte man wissen
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n Q=1-P
W bei Binomialverteilung (bei Ziehung ohne
WDH) und: wenn n/N <0,05 kann die HV durch
die BV genähert werden
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n
Erwartungswert von r bei Binomialverteilung
und hypergemetrischer Verteilung
Var(r|n,P) Var(r|n,P)=n*P*Q
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n Q=1-P
Durchschnittliche Abweichung ² bei
Binomialverteilung
Var(p|n,P)
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n Q=1-P p=r/n
Durchschnittliche Abweichung von p ² bei
Binomialverteilung
W (r)
W (r)=(n über r)*P^r*Q^(n-r)
E(r|n,P)
E(r|n,P)=n*P
Var(p|n,P)=P*Q/n
or
or=WURZEL(P*Q*n)
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n Q=1-P
Durchschnittliche Abweichung
op
op=WURZEL(P*Q/n)
n= Gesamtmenge der Elemente r= günstige
Menge der Elemente P=r/n Q=1-P p=r/n
Durchschnittliche Abweichung von p
N= Gesamtmenge der Elemente R= günstige
W bei hypergeometrischer Verteilung (ohne
W(r|n,N,R) W(r|n,N,R)=(R über r)*(N-R über n-r)/N über n Menge der Elemente n= Anzahl der Ziehungen
Zurücklegen)
r= Anzahl des gewünschten Eintreffens
Var
(r|n,N,R)
18.04.02
Var (r|n,N,R)= n*P*Q*(N-n)/(N-1)
N= Gesamtmenge der Elemente R= günstige
Varianz von r bei hypergeometrischer
Menge der Elemente n= Anzahl der Ziehungen
Verteilung
r= Anzahl des gewünschten Eintreffens
Sascha Tünker
FB 02 Wirtschaftswissenschaften
Seite 4 von 5
sollte man wissen
Var
(p|n,N,R)
W (r)
u
W(xxquer)
Var (p|n,N,R)=P*Q/n*[(N-n)/(N-1)]
W (r) =Fi(u) lt. Tabelle Fi(u+)=1-Fi(u-) und
umgekehrt; Fi (u+-)=Fi(u+)-Fi(u-)
18.04.02
NV kann zur Näherung der BV und HV
verwendet werden, wenn n*P*Q>9
u-=(Gu-X)/ox; u+=(Go-X)/ox; u+-=(Go-Gu)/2ox Wird für NV benötigt
W(|X-xquer|<=c*ox)>=1-1/c²
Lambda lambda=n*P
W (r)
N= Gesamtmenge der Elemente R= günstige
Varianz von p bei hypergeometrischer
Menge der Elemente n= Anzahl der Ziehungen
Verteilung
r= Anzahl des gewünschten Eintreffens
W (r) =lamda^r*e^lambda/r!
Wahrscheinlichkeit von r bei Normalverteilung
normierte Zufallsvariable u
Die Wahrscheinlichkeit, dass ein Wert innerhlb
Tschebytscheffsche Ungleichung
des Intervalls c*ox liegt, ist >= 1-1/c²
braucht man halt
wird für Poissont-Verteilung benötigt
Näherung für BV und HV, wenn n sehr groß
Poissont-Verteilung
Sascha Tünker
FB 02 Wirtschaftswissenschaften
Seite 5 von 5