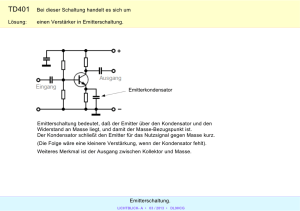
1. Ein Dielektrikum im Kondensator 2. Veränderung an der

Arbeitsblatt
Anwendungen am Kondensator
Grundkurs Physik 11
1. Ein Dielektrikum im Kondensator
Was passiert mit einem Körper aus Isolatormaterial (z.B. ein Stück Styropor), wenn man ihn zwischen die Kondensatorplatten
bringt? Untersuchen Sie dies mit dem Teilchenmodell der Materie.
1. Tragen Sie in die Skizze des Stücks Styropor zwischen die Kondensatorplatten die Atomrümpfe ein.
2. Skizzieren Sie, wie sich die an die Atomrümpfe gebundenen Elektronen unter dem Einfluss des äußeren Feldes
ausrichten.
3. Tragen Sie das elektrische Feld ein, das zwischen dem Atomrümpfen und ihren Elektronen auf Grund der Polarisation
bildet.
4. Entscheiden Sie, ob das elektrische Feld im Styropor das äußere abschwächt oder verstärkt und ob die Zahl der im
Kondensator gespeicherten getrennten Ladungen vergrößert oder verringert wurde?
5. Die Gleichung für die Kapazität eines Plattenkondensators wird für Dielektrika (lat. Plural) durch den Faktor εr
modifiziert. Je stärker der Isolator, desto größer wird diese Dielektrizitätszahl εr . Welche Formel ist korrekt? (Wann
fasst der Kondensator mehr Ladungen?)
(A)
A
C =εr⋅ε0⋅
d
(B)
ε A
C = ε 0⋅
r d
6. Bestimmen Sie die Dielektrizitätszahlen der Luft und des Vakuums!
2. Veränderung an der Kondensatoranordnung
Viele moderne Geräte wie z.B. kapazitive Touchscreens nutzen den Zusammenhang aus, dass durch mechanische Veränderung
des Kondensatoraufbaus die elektrischen Größen Spannung und Ladung gezielt beeinflusst werden können. Dies hängt davon
ab, ob der Kondensator weiterhin an eine Spannungsquelle angeschlossen ist. Daher betrachten wie die beiden Fälle
(Anmerkung: Dies kann man zwar wie oben durch Modellvorstellungen erschließen, aber nun sollen Sie dies mit Hilfe der
Interpretation der Gleichungen.)
7. Fertigen Sie die folgende Tabelle an (Sie brauchen weniger Platz in der Mitte!) und vervollständigen Sie diese.
Kondensator an der
Spannungsquelle
Kondensator von der
Spannungsquelle getrennt
Welche Größe bleibt konstant: Q oder U?
Q=…
Stellen Sie die Gleichung für die Ladung eines Kondensators um auf
die jeweils andere Größe (mit Dielektrizitätszahl!).
U= …
Benennen Sie die physikalischen Größen in den Gleichungen!
Q ̴ …
Q ̴…
2x → 2Q
2y → 0,5Q
Beschreiben sie die mathematischen Zusammenhänge zwischen der
Ladung bzw. der Spannung am Kondensator und den übrigen Größen
(inklusive der Dielektrizitätszahl).
U ̴ …