Einführung zum Oszilloskop

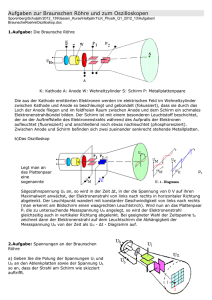
4.
Das Oszilloskop
4.1
Allgemeines
Das Oszilloskop ist das universellste Instrument der physikalischen bzw. elektrischen Messtechnik. Es
wird primär zur Darstellung von zeitlich schnell veränderlichen Signalen auf einem Bildschirm verwendet. Neben dem klassischen Oszilloskop, das eine reale Elektronenstrahlröhre enthält, gibt es
heute auch verschiedenste elektronische Einrichtungen zur Signalanalyse und Signaldarstellung, die
in Verbindung mit einem PC die Funktionen eines Oszilloskops mehr oder weniger vollständig erfüllen
können. Auf sie wird später eingegangen.
4.2
Die Elektronenstrahlröhre
Die Elektronenstrahlröhre („Braun‘sche Röhre“) ist das eigentliche „Messwerk“ des Oszilloskops.
Praktisch besteht die Elektronenstrahlröhre aus einem langgestreckten, evakuierten Glaskolben,
in dessen hinteren Teil ein Strahlerzeugungssystem („Elektronenkanone“) sitzt, das einen feinen
Elektronenstrahl (quasi als fast trägheitslosen Zeiger) in Richtung des vorne angebrachten Leuchtschirms sendet der dort am Auftreffpunkt einen Leuchtpunkt erzeugt. Durch ein x- und ein yAblenksystem lässt sich der Elektronenstrahl entsprechend einer x- und einer y-Signalspannung an
jeden Punkt des Schirms steuern. Es kann somit jeder Punkt der Funktion y  f (x) in einem
Kartesischen Koordinatensystem dargestellt werden.
Das Strahlerzeugungssystem besteht aus einen System mehrerer Elektroden. In der
Kathode werden durch sog. Glühemission Elektronen aus einer Metalldrahtoberfläche ausgelöst. Die
Anode befindet sich gegenüber der Kathode auf positivem Potenzial, sodass die Elektronen in
Richtung zur Anode beschleunigt werden. Die Anode hat ein kreisförmiges Loch, sodass sich
Elektronen in Richtung zum Schirm als Elektronenstrahl weiterbewegen können. Der Schirm ist
gegenüber der Anode auf noch höherem positiven Potenzial und beschleunigt somit die durchgetretenen Elektronen weiter. Durch ein System von weiteren Hilfselektroden im Raum zwischen
Kathode und Anode kann der Elektronenstrahl gebündelt werden, wobei diese Hilfselektroden sich
gegenüber der Kathode auf negativem Potenzial befinden und somit der Tendenz der Elektronen, sich
gegenseitig abzustoßen, entgegenwirken. Weitere Hilfselektroden steuern die Zahl der pro Zeiteinheit
fließenden Elektronen (also den Elektronen“strom“ im Vakuum).
Schirm
K
W
L
A
Y
X
Y
X
X
Y
Abb.4.1
Elektronenstrahlröhre, schematischer Aufbau
Die Ablenkeinheit nutzt den Effekt der Ablenkung von sich bewegenden Elektronen im elektrischen
Feld. Ein Plattenpaar, dessen Feld in x-Richtung orientiert ist und eines mit y-Orientierung erlauben
die Steuerung des Leuchtpunktes an jeden beliebigen Ort ( D x , D y ) des Schirms.
Zwischen den parallelen Platten eines unter Spannung stehenden Kondensators entsteht
bekanntlich ein homogenes elektrisches Feld, dessen Feldstärke E der angelegten Spannung U
proportional ist. Ein parallel zu den Platten bewegtes Elektron erfährt eine Kraftkomponente FE in
Feldrichtung und wird durch sie entsprechend beschleunigt. Ist z die ursprüngliche Flugrichtung des
Elektrons, dann hat es beim Eintritt in den Kondensator nur die Geschwindigkeitskomponente v z ,
beim Austritt aus den (z. B.) y-Platten ist sein Geschwindigkeitsvektor um die Komponente v y vergrößert. Als Folge verlässt das Elektron am Ende den Kondensator unter einem Winkel
sprünglichen Flugrichtung:
tan  
vz
vy
zur ur-
(4.1)
vz
vy
q
++++++++
d

v
DY
vz
- - - - - - - -
l
Abb.4.2
L
Ablenkung eines Elektrons im Kondensatorfeld der Ablenkplatten
Die Geschwindigkeitskomponente
v y berechnet sich aus der Beschleunigung a y und der Verweilzeit
t im Kondensator. Die Beschleunigung a y ihrerseits ergibt sich aus der Kraft Fy , diese wiederum
ergibt sich aus der Feldstärke
E y beziehungsweise aus der angelegten Spannung U y und dem
d . Dabei ist me die Elektronenmasse:
Plattenabstand
v y  a y t 
Fy
me
t 
e Ey
me
t 
eUy
me d
t
(4.2)
Die Verweilzeit t ist durch die Geschwindigkeitskomponente v z und die Kondensatorlänge
geben:
t 
l
vz
womit der Zusammenhang mit dem Ablenkwinkel
tan  
Die Ablenkung
e Ux l
me d v z2
(4.3)

entsteht:
(4.4)
D y am Schirm ergibt sich schließlich wie folgt, wobei L der Abstand vom
Kondensatorausgang bis zum Schirm ist:
l ge-
Dy 
e l 1
Uy
me L d v z2
Somit trifft der Strahl mit einer Ablenkung
spannung
(4.5)
D y am Schirm auf, die der angelegten Kondensator-
U y proportional ist. Eine völlig analoge Überlegung gilt für die x-Komponente.
Die Bewegung des Elektrons im Kondensator entspricht der eines waagrecht abgeworfenen
Massepunkts im Gravitationsfeld der Erde („Wurfparabel“).
Der Quotient aus Ablenkung Di und Spannung U i am jeweiligen x- bzw. y-Kondensator wird
Ablenkempfindlichkeit genannt. Sie ist für eine vorgegebene Röhre eine Konstante und liegt bei
einfachen Universaloszilloskopen bei etwa 1cm/100V. Üblicherweise will man mit kleineren
Signalspannungen eine merkbare Auslenkung erzielen, daher müssen die Signale in einem entsprechenden Spannungsverstärker verstärkt werden. Solche Verstärker haben einen hohen, fixen
Verstärkungsfaktor und sind vor den Ablenkplatten eingebaut. Um sich an alle vorkommenden
Spannungen anpassen zu können, ist zwischen Signaleingang und Spannungsverstärker noch der
variable „Abschwächer“ (Widerstandsnetzwerk) vorgeschaltet, der die Signalspannung entsprechend
seiner Einstellung reduziert. Üblicherweise sind die Ablenkempfindlichkeit der Röhre und der Verstärkungsfaktor des Verstärkers für den Benutzer uninteressant, wichtig ist nur die letztendlich
resultierende effektive Ablenkempfindlichkeit, also der Zusammenhang zwischen Eingangsspannung und Ablenkweite. Diese wird am entsprechenden Schalter für den Abschwächer angezeigt
(Einheit: V/div.) und zwar in den Stufen: 5-10-20-50-100-200-500mV-1-2-5-10V/div. Eine kontinuierliche Einstellung der effektiven Ablenkempfindlichkeit ist ebenfalls möglich, sie wird mit dem Hinweis
„uncal.“ angezeigt und sollte normalerweise nicht benutzt werden, um falsche Ablesungen zu vermeiden.
4.3
Die Zeitablenkung
Wichtigste Aufgabenstellung mit dem Oszilloskop ist die Darstellung des zeitlichen Verlaufs eins zeitlich periodischen Spannungsverlaufs im Sinne einer Funktion y = f(t), wobei die Zeit t wie bei entsprechenden Diagrammen entlang der x-Achse aufgetragen wird. Dazu wird der Elektronenstrahl mit
konstanter Ablenkgeschwindigkeit in x-Richtung abgelenkt und gleichzeitig in y-Richtung das zu untersuchende Signal angelegt. Der Punkt auf dem Schirm beschreibt dann eine Bahn, die dem zeitlichen
Verlauf der zu analysierenden Spannung entspricht.
Im Falle eines periodischen Signals wird der horizontale Ablenkvorgang (x) ständig wiederholt,
sodass auf dem Bildschirm ständig eine neue Kurve entsteht. Die diese x-Ablenkung hervorrufende
Spannung erzeugt ein im Gerät eingebauten Generator, der periodisch eine zeitlich kontinuierlich ansteigende Spannung generiert („Sägezahnspannung“), die nach Erreichen ihres Höchstwerts wieder
auf den Ausgangswert zurückspringt.
Im Allgemeinen ist dieser sog. „unsynchronisierte“ Betrieb ziemlich unbrauchbar, da ein
stationäres Bild des zeitlichen Signalverlaufs nur in speziellen Fällen entsteht, nämlich wenn die
Sägezahnspannung und die untersuchte Signalspannung Frequenzen aufweisen, die exakt ganzzahlige Vielfache voneinander sind. Siehe Abb.5.3.oben.
Üblicherweise möchte man aber zeitlich periodische Signale mit beliebiger Frequenz analysieren und als stehendes Bild beobachten. Um dabei die nötige Phasensynchronität zwischen
Signalspannung und Sägezahnspannung zu erreichen, muss vor dem Neustart eines jeden Sägezahns solange gewartet werden, bis die Signalspannung dieselbe Phase hat, wie beim vorigen mal.
Dieses Erkennen der Phase und Starten des jeweils neuen Sägezahns erledigt die sog. Triggereinrichtung im O. (trigger, engl., ist der Abzug beim Gewehr).
Der „Trigger“ ist ein Spannungskomparator, der ständig die Signalspannung mit einer vorwählbaren internen Spannung („Triggerspannung“, „Triggerniveau“) vergleicht. Übersteigt das
Signal das Triggerniveau, dann wird die Zeitablenkung gestartet bzw. der nächste Sägezahn ausgelöst. Durch Einfügen dieser „Wartezeit“ werden bei jeder Ablenkung immer exakt dieselben Kurven
übereinandergeschrieben, es entsteht ein stehendes Bild. Siehe Abb. 4.3. unten.
Neben der Wahl des Triggerniveaus kann der Trigger auch so eingestellt werden, dass beim
Unterschreiten einer bestimmten Spannung die Zeitablenkung gestartet wird („Triggern auf die
negative Flanke“).
Uy
Zeit
Ux
Uy
Utrig.
Zeit
Ux
Wartezeit
Abb.4.3
Unsynchronisierter (oben) und getriggerter Betrieb (unten) der Zeitablenkung:
Signalspannung und Sägezahnspannung. Die offenen Punkte geben den Startpunkt
der x-Ablenkung wieder
Für Spezialzwecke kann der Trigger auch von einer externen Signalquelle ausgelöst werden. Dafür
steht ein zusätzlicher externer Triggersignaleingang (ext. Trig.) zur Verfügung und es muss beim
Wahlschalter für die Triggerart von intern auf extern umgeschaltet werden.
Der zeitliche Anstieg der Ablenkspannung (Sägezahnspannung) und somit die Schreibgeschwindigkeit in x-Richtung werden am Zeitbasis-Wahlschalter in Stufen von 1,2,5,10 s/Div. bzw. in entsprechenden Untereinheiten eingestellt. Eine stufenlose Einstellung ist ebenfalls möglich („uncal.“)
sollte jedoch im Allgemeinen wegen der Gefahr von Fehlmessungen vermieden werden.
4.4
Zweikanalbetrieb
Eine häufige Fragestellung in der physikalischen Messtechnik und Elektronik ist, wie sich ein zeitlich
periodisches Signal beim Durchgang durch eine bestimmte Schaltung verändert. Man muss also
gleichzeitig das Signal vor und das Signal nach der betreffenden Schaltung zeitsynchron beobachten
können. Dies ermöglicht der sog. Zweikanalbetrieb des Oszilloskops. Dazu dienen zwei identische,
voneinander unabhängige Y-Eingänge, die als zwei getrennte Strahlen mit identischer Zeitablenkung
dargestellt werden.
Die Herstellung der zwei Strahlen geschieht entweder alternierend (alt) oder „gechoppt“
(chop). Im alternierenden Betrieb wird beim x-Ablenkungsvorgang durch einen automatischen
elektronischen Umschalter von Durchlauf zu Durchlauf abwechselnd einmal das Signal des ersten
resp. des zweiten Kanals dargestellt. Beim gechoppten Betrieb erfolgt diese Umschaltung mit großer
Häufigkeit innerhalb einer x-Ablenkperiode, sodass jeweils nur kleine Stücke des entsprechenden YSignals geschrieben werden und somit jeweils als zusammenhängendes Signal gesehen werden.
Wegen der Zeitsynchronität beider Strahlen können im Zweikanalbetrieb Änderungen
wichtiger Signalparameter wie Signalform, Amplitude und relative Phase etc. beobachtet werden.
Die interne Triggerung im Zweikanalbetrieb kann entweder auf das Signal des Kanals 1 oder
des Kanals 2 erfolgen (oder externe Triggerung).
4.4.1
Addition und Subtraktion von Signalen.
Beide Y-Eingänge können auch intern elektronisch summiert (ADD) werden. Ein Y-Kanal ist
außerdem noch invertierbar (invert), sodass auch die Möglichkeit der Differenzsignalbildung gegeben
ist. Über die individuellen Empfindlichkeitseinstellungen der beiden Y-Kanäle lassen sich beide
Signale auch noch hinsichtlich ihrer Amplitude unterschiedlich gewichten.
4.5
XY-Betrieb
Einer der beiden Y-Kanäle des Oszilloskops kann auch als extern anzusteuernder X-Kanal (ext. X)
geschaltet werden. Diese sog. XY-Darstellung bietet eine elegante und schnelle Methode der Darstellung von Frequenz- und Phaseverhältnissen zwischen zwei zeitlich periodischen Signalen. Sind
die Frequenzen der beiden Signale auf dem X- und Y- Kanal ganzzahlige Vielfache voneinander, so
sieht man am Schirm eine sog. „Lissajous-Figur“.
Haben beide Signale gleiche Frequenz, jedoch eine Phasenverschiebung zueinander, so ist die Phase aus der entstehenden Lissajous-Ellipse wie folgt zu bestimmen:
Zuerst werden die Empfindlichkeiten beider Kanäle so eingestellt, dass beide Amplituden
gleich groß dargestellt werden, dann erscheint eine Ellipse, deren große Hauptachse unter
45 Grad zur Waagrechten verläuft (Siehe Abb. 4.4). (Ist die Phasenverschiebung null, entartet die Ellipse zu einer 450-Geraden).
Ist die y-Ablenkung gegenüber der x-Ablenkung um die Phase
und y-Koordinaten der Ellipse durch folgende Gleichungen gegeben:

verschoben, so sind die x-
x  x1 cos t
y  y1 cos(t   )
(4.1)
(4.2)
Die aus dem Oszilloskopbild abzulesende Strecke B in Abb.4.4. beträgt 2 y genau zu dem Zeitpunkt,
in dem
x  0 ist, was aber wegen (4.1) bedeutet, dass in diesem Zeitpunkt t  

2
sein muss.
Dann gilt:
y  y1 cos(

2
  )   y1 sin 
(4.3)
Daraus folgt, dass B  2 y  2 y1 sin  ist.
Das Doppelte der maximalen Auslenkung in y-Richtung sei entsprechend Abb.4.4. mit A bezeichnet und entspricht dem Doppelten der y-Amplitude: A  2 y max  2 y1 . Somit gilt für das Verhältnis B/A bzw. für die Phasenverschiebung
B
 sin 
A
bzw.
:
  arcsin
B
A
(4.4)
Es sind also zur Bestimmung der Phasenverschiebung zwischen den beiden Signalen nur die
maximale Höhe der Ellipse und ihre Abmessung bei x  0 zu bestimmen und in einzusetzen.
Allerdings ist das Ergebnis nicht eindeutig, sodass man schon vorher wissen muss, in welchem Bereich die Phase sich etwa bewegt.
B=2 y1 sin
A=2 y1
Abb.4.4.
4.5
Zur Bestimmung der Phase zwischen zwei sinusförmigen Signalen bei xy-Darstellung
Digitaler Speicherbetrieb
In der physikalischen Messtechnik kann es vorkommen, dass man den Zeitverlauf eines schnellen
einmaligen Vorgangs mit dem Oszilloskop darstellen möchte. Dazu wird das Y-Signal in der zeitlichen
Länge der eingestellten Ablenkperiodendauer in einen elektronischen Speicher geschrieben und von
dort heraus periodisch ausgelesen und als periodisches Signal an die Elektronenstrahlröhre gelegt,
sodass nach erfolgtem Speichervorgang ein stationäres Bild entsteht.
Bei der Triggerwahl ist dabei auf Einzelablenkung (single sweep) zu schalten, um ein ungewolltes Überschreiben des Speicherinhalts zu vermeiden.
Weiters kann man den digitalen Speichermodus bei langsamen periodischen Signalen benutzen, bei denen im Normalbetrieb kein stationäres Bild entstehen würde, um trotzdem zu einem
solchen zu kommen.
4.6
Tipps zum Umgang mit dem Oszilloskop
Beim praktischen Arbeiten mit dem Oszilloskop empfiehlt es sich, zu Beginn der Messung das Oszilloskop in den Grundzustand zu versetzen, und von dort weg die speziellen Einstellungen systematisch
vorzunehmen.
1. Grundeinstellung vornehmen
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1.10.
1.11.
Netzschalter: ein ?
Store: aus?
x-y Betrieb: aus ?
Trigger ext.: aus ?
Trigger: auto ?
Zweikanalbetrieb: ein ?
Ch1, Ch2: GND ?
Ch1, Ch2: invert aus ?
YPos1, YPos2: Mitte ?
x-Pos: Mitte ?
Time: z. B.: 1 ms/div.: ein ?
(kein Speicherbetrieb)
(automatische Triggerung)
(Eingangssignale auf null)
Jetzt sollten die beiden Strahlen als horizontale Linien sichtbar sein.
2. Periodisches Signal darstellen
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
Ch1,Ch2: cal. ?
Time: cal ?
Ch1,Ch2: Y-Pos. gewählt?
(Lage der Nulllinien)
Ch1,Ch2: V/Div. angepasst ?
Ch1,Ch2: DC ?
Trigger: Norm., Ch1 od. Ch2, DC ?
Trigger: Level, Flanke (+,-) angepasst?
Jetzt sollte das Signal als stehendes Bild sichtbar sein.
3. Signalspeicherung, periodisches Signal
(REFRESH-Betrieb, d. h. ständige Wiederholung des Speicherbetriebs)
3.1.
3.2.
3.3.
3.4.
3.5.
Store: ein ?
Hold: aus ?
Single: aus ?
Time: angepasst ?
Trigger: wie 2.6.,2.7.
LED leuchtet!
(Speicherbetrieb eingeschaltet)
(fixiert den Speicherinhalt)
Jetzt sollte ein stehendes Bild sichtbar sein, das ständig überschrieben wird.
3.6.
Hold: ein: Der Speicherinhalt wird fixiert, z. B. für Transfer zum PC
Helmut Feichtinger, Alfred Leitner: Einführung in die Physikalischen Messmethoden. Institut für
Experimentalphysik, KFUG (http://www.uni-graz.at/expwww/messmskript05.pdf, 1.9.2010)