Anwesenheitsübung 2

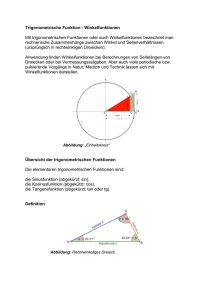
Anwesenheitsübung zur Physik für
Nicht-Physikerinnen und Nicht-Physiker
(SoSe 14)
Prof. W. Meyer
Übungsgruppenleiter: A. Berlin & J. Herick (NB 2/28)
Anwesenheitsübung 2
Ein weiteres wichtiges Gebiet sind die Winkelfunktionen. Es gibt einen richtigen Zoo von Winkelfunktionen, aber die wichtigen sind nur die ersten drei Funktionen, Sinus, Kosinus und Tangens.
Der Winkel
Aber zunächst noch ein Hinweis. In der Physik werden Winkel im Allgemeinen nicht im Grad-Maß
angegeben, sondern im rad-Maß. Wir wissen, dass ein Kreis 360° hat – eine Umdrehung. Und wir
kennen den Umfang eines Kreises U = 2π · r. Ein Einheitskreis hat somit einen Umfang von U = 2π m
(da r=1 m ist).
Aus diesen beiden Eckdaten können wir sagen, dass 360°– ein Vollkreis – genau 2π rad entsprechen.
also
und
360° =
b
2π rad
180° =
b
b
57, 3° ≈
π rad
und
1 rad
b
1° ≈
0,0175 rad
Die Umrechnung geht dann wie folgt:
α[ rad] =
π
· α[°]
180
Bei der Benutzung eines Taschenrechners muss darauf geachtet werden welches Winkelmaß eingestellt ist, wenn man mit Winkelfunktionen rechnet (grad- oder rad-Maß).
Winkelfunktionen
Die Winkelfunktionen sind definiert als Seitenverhältnisse rechtwinkliger Dreiecke; also einem Dreieck bei dem ein Winkel 90° beträgt.
C
=
90
a
sin α
cos α
A
62
a
c
Hypotenuse
b
a
Gegen-Kathete
An-Kathete
g = 90°
zu
tan α =
An-Kathete
Hypotenuse
a
te
Tangens:
=
zu
te
the
a
-K
b
An
e
ath
cos α
Gegen-Kathete
Hypotenuse
28
Kosinus:
=
n-K
ge
sin α
Ge
Sinus:
B
Dabei bezeichnet α den Winkel um den es geht; die Hypotenuse ist die längste Seite des rechtwinkligen Dreiecks (gegenüber des rechten Winkels); die An-Kathete ist die Seite, die an dem entsprechenden Winkel liegt und die Gegen-Kathete ist die Seite des rechtwinkligen Dreiecks, welche
dem Winkel gegenüberliegt.
Umkehrfunktion zu den Winkelfunktionen
Möchte man an den Winkel berechnen, so muss die jeweilige Umkehrfunktionen verwendet werden.
Zum Sinus gehört der Arkussinus, zum Kosinus der Arkuskosinus und zum Tangens der Arkustangens.
Übliche Schreibweisen für den Arkussinus sind z.B. arcsin , asin oder sin−1 .
z.B.
arcsin(sin α) = α
Winkelfunktionen in einem anderen Kontext
90° - p/2 rad
y
1
s
a
180° - p rad
sin a
60
Eine erweiterte Sichtweise auf diese Funktionen
bekommt man im Einheitskreis (Ein Kreis mit
dem Radius 1 m).
Betrachtet wird hier ein Punkt, der sich auf dem
Umfang des Einheitskreises bewegt. Die Verbindungslinie zwischen diesem Punkt und dem Mittelpunkt ~s kann als ein Vektor aufgefasst werden,
hier in 2D. Durch die Bewegung entlang des Umfangs ändert sich auch der Winkel (hier α) welcher der Verbindungsvektor ~s mit der x-Achse bildet.
x
cos a
1
0° - 0 rad
360° - 2p rad
270° - 3/2 p rad
Mann kann nun die Winkelfunktionen als eine Projektion auf die Achsen verstehen. Dabei ist der
Sinus von α die Projektion von ~s auf die y-Achse und der Kosinus die Projektion des Vektors auf die
x-Achse.
~s = (sx , sy )
sx = |~s| · cos α
sy = |~s| · sin α
Man erkennt an diesem Beispiel auch gut die Periodizität (wiederkehrende Eigenschaft) der Winkelfunktionen, denn nach einer Umdrehung (2π rad) ist man wieder am Ausgangspunkt angekommen.
[Bsp. sin(α) = sin(α[°] + 360°) = sin(α + 2π)].
Grad
0
Trägt man die Funktionen gegenüber dem
Winkel auf, wird einem die Periodizität
noch deutlicher:
180
360
540
720
900
4p
5p
Sinus
Kosinus
1
0
Zu beachten ist auch, dass die Funktionswerte für Sinus und Kosinus lediglich zwischen 1 und -1 schwanken.
-1
0
p
2p
3p
Radian
Zum Schluss noch ein paar Sätze zu Dreiecken.
– Die Summe aller Winkel im Dreieck ist immer 180° (oder π rad)
– Im rechtwinklingen Dreieck gilt der Satz des Pythagoras a2 + b2 = c2 .
a,b sind die Seitenlängen der Katheten und c die der Hypotenuse.
Aufgabe 1: Winkelsumme
Bestimmen Sie die unbekannten Winkel
g
a) α = 27° und β = 81°
98
45
b) α = 112° und γ = 63°
a
37
c) α ist um 20° größer als β und β ist halb so groß wie γ
b
d) β ist doppelt so groß wie α und γ ist dreimal so groß wie α
e)
f)
C
g
C
74°
g
b
64°
A
140°
A
a
b 137°
B
B
Aufgabe 2: Satz des Pythagoras
a) Eine Boje ist an einer Kette befestigt. Die Boje kann 1 m aus dem
Wasser gezogen werden oder sie kann 3 m zur Seite abdriften.
Wie lang ist die Kette?
3m
5m
b) Ein Flugzeug fliegt 165 km nach Norden, dann 220 km nach Westen.
Wie weit wäre der direkte Flug gewesen?
c) Ein Haus soll ein neues Dach bekommen.
Wie viel Quadratmeter Dachpfannen müssen gekauft werden?
12 m
8m
Aufgabe 3: Winkelfunktionen
C
Berechnen Sie die im rechtwinkligen Dreieck jeweils fehlenden Seiten und Winkel (a,b,c,α und β):
I) q = 5
II) h = 9
b
β = 70°
h
a
p=6
Für die ganz schnellen
III) a = 28
90
A = 373 (Fläche)
IV) a : b = 3 : 4
U = 60 (Umfang)
A
a
b
90
B
c
p
q