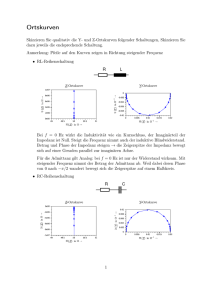
- Institute for Applied Geophysics and Geothermal Energy

Induktive Kabelkopplungseffekte bei Messungen der
Spektral Induzierten Polarisation
von
Andreas Pawlik
Diplomarbeit in Physik
vorgelegt der
Fakultät für Mathematik, Informatik und Naturwissenschaften
der Rheinisch-Westfälischen Technischen Hochschule Aachen
im Januar 2008
angefertigt am
Lehrstuhl Applied Geophysics and Geothermal Energy
im E.ON Energy Research Center, RWTH Aachen University
Berichter:
Prof. Dr. C. Clauser
Prof. Dr. G. Güntherodt
i
Ich versichere hiermit, die vorliegende Arbeit selbständig verfasst und keine anderen
als die angegebenen Quellen und Hilfsmittel benutzt zu haben.
Aachen, Dezember 2007
Andreas Pawlik
ii
Danksagung
Ich danke Herrn Prof. Dr. Christoph Clauser für die Möglichkeit, diese Arbeit am
Lehrstuhl Applied Geophysics and Geothermal Energy durchzuführen und die Einrichtungen
des Instituts nutzen zu dürfen. Ich bedanke mich auch für die gute Betreuung, die vielen
Anregungen und Gespräche sowie die Begutachtung der Arbeit.
Besonders herzlich danke ich Herrn Dr. Norbert Klitzsch für die hervorragende
Betreuung meiner Arbeit und die Zeit, die er sich stets für Gespräche und Anregungen
genommen hat sowie die unzähligen Stunden, die er mich bei den Messungen im Feld
unterstützt hat.
Mein Dank gilt weiterhin Herrn Prof. Dr. Gernot Güntherodt für Zweitkorrektur sowie
Herrn Dr. Volker Rath für die Möglichkeit, das Programm IP3C zu nutzen und mich bei
Fragen immer an ihn wenden zu können. Außerdem danke ich Frau Natalia Günther und
Herrn Daniel Wegner für die unschätzbare Hilfe bei der Programmierung der MatlabProgramme. Für die gute Zusammenarbeit bei Feldmessungen danke ich Herrn Adrian Flores
Orozco, Frau Caroline Wygasch und Herrn Jens Protze.
Ich danke darüber hinaus allen Mitarbeitern des Lehrstuhls Applied Geophysics and
Geothermal Energy für ihre Hilfsbereitschaft und die freundliche Arbeitsatmosphäre.
iii
Inhaltsverzeichnis
1
EINLEITUNG ................................................................................................... 1
2
THEORIE ......................................................................................................... 4
2.1
Der IP-Effekt .................................................................................................. 4
2.2
Membranpolarisation ..................................................................................... 4
2.3
Elektrodenpolarisation ................................................................................... 5
2.4
Messungen...................................................................................................... 8
2.5
Spektrale IP .................................................................................................. 12
2.6
Relaxationsmodelle ...................................................................................... 14
2.6.1
2.7
3
4
Cole-Cole-Modell..................................................................................... 14
Kabelkopplungseffekte................................................................................. 15
2.7.1
Kapazitive Kabelkopplung....................................................................... 16
2.7.2
Induktive Kabelkopplung......................................................................... 20
2.8
Das Messgerät SIP256C............................................................................... 25
2.9
Das Programm IP3C..................................................................................... 26
SENSITIVITÄTSSTUDIEN ............................................................................... 28
3.1
Motivation .................................................................................................... 28
3.2
Homogener Halbraum .................................................................................. 29
3.3
Zweischichtfall ............................................................................................. 39
3.4
Dreischichtfall .............................................................................................. 43
3.5
Einfluss von Kabelanordnung und -länge .................................................... 47
3.6
Zusammenfassung der Sensitivitätsstudien.................................................. 52
FELDMESSUNGEN ......................................................................................... 53
4.1
Motivation .................................................................................................... 53
4.2
Einfluss der Kabelanordnung ....................................................................... 53
4.3
Einfluss der Kabellänge ............................................................................... 58
4.4
Einfluss des Dipolabstands........................................................................... 59
4.5
Tiefensektionen ............................................................................................ 61
iv
4.6
Probleme bei der Korrektur der Daten ......................................................... 71
5
ZUSAMMENFASSUNG UND AUSBLICK........................................................... 73
6
LITERATURVERZEICHNIS ............................................................................. 75
7
ANHANG........................................................................................................ 78
A.1
Der Frequenzeffekt....................................................................................... 78
A.2
Das Cole-Cole Modell.................................................................................. 78
A.3
Der Term Q(R) ............................................................................................. 79
Einleitung
1
1 Einleitung
In dieser Arbeit werden induktive Kabelkopplungseffekte untersucht, die bei
frequenzabhängigen elektrischen Messungen (Methode der Spektral Induzierten Polarisation SIP) auftreten. Da diese Kopplungseffekte die Messdaten überlagern, ist das Ziel dieser
Arbeit die Simulation der induktiven Kopplungseffekte und die Korrektur gemessener SIPDaten.
SIP ist ein geoelektrisches Verfahren der angewandten Geophysik, bei dem
Wechselstrom verschiedener Frequenzen in den Untergrund eingespeist wird, um den
komplexwertigen spezifischen Widerstand zu messen. Das Maß für die Polarisation ist dabei
die Phasenverschiebung zwischen Strom und Spannung. Im Unterschied zur Induzierten
Polarisation (IP), bei der Wechselstrom einer bestimmten Frequenz verwendet wird, erstreckt
sich das Frequenzband bei SIP typischerweise über mehrere Dekaden (oft 1 mHz bis
1 kHz). Es handelt sich um ein Verfahren, das an der Oberfläche eingesetzt werden kann.
Dadurch ist es relativ kostengünstig und vielseitig einsetzbar.
Anwendung finden SIP und IP bei der Exploration mineralischer Erzlagerstätten sowie
der Erkundung industrieller Altstandorte und Deponien. Noch in der Forschungsphase ist der
Einsatz für hydrogeologische Fragestellungen, wie die Ableitung der hydraulischen
Permeabilität.
Der Effekt der Induzierten Polarisation (IP) ist seit Beginn des zwanzigsten
Jahrhunderts bekannt, als er von den Gebrüdern Schlumberger entdeckt wurde. Conrad
Schlumberger beobachtete 1920 bei elektrischen Messungen an Gesteinen, wie die Spannung
nach Abschalten des Stroms nicht sofort auf Null abfiel, sondern zunächst auf einen endlichen
Restwert, von dem aus sie langsam auf Null abklang [Schlumberger, 1922]. Das Gestein
wurde polarisiert. Man prüfte darauf hin, ob sich der Effekt für geophysikalische
Erkundungen eignet, kam jedoch zu keinen brauchbaren Ergebnissen.
Der IP wurde lange Zeit keine Beachtung geschenkt, bis in der Nachkriegszeit der
Bedarf an Rohstoffen, vor allem Erzen, drastisch anstieg und man die Möglichkeiten des
Verfahrens bei der Erzexploration erkannte [Bleil, 1953]. Durch die unterschiedlichen
Polarisationen von vererztem und nicht vererztem Gestein, die mit IP abgebildet werden
können, gewann es für die Explorationsindustrie mehr und mehr an Interesse.
Das Verfahren konnte in den Folgejahren weiter verfeinert werden, sodass auch
kleinere Polarsationsunterschiede aufgelöst werden konnten.
Einleitung
2
In den siebziger Jahren wurde damit begonnen, Gesteinsproben über breite
Frequenzspektren hinweg zu vermessen [van Voorhis et al., 1973], [Zonge und Wynn, 1975],
[Pelton et al., 1978]. Daraus entwickelte sich schließlich das Verfahren der SIP, im
angloamerikanischen Raum oft auch Complex Resisivity (CR) genannt. Das war eine
entscheidende Weiterentwicklung, die nunmehr das Formulieren neuer Ziele zuließ. So wollte
man nicht mehr nur mineralisierte von nicht mineralisierten Bereichen unterscheiden, sondern
innerhalb dieser Bereiche weitere Unterscheidungen vornehmen. Pelton et al. [1978] sowie
Major und Silic [1981] zeigten, dass SIP zur Unterscheidung graphitischer Ablagerungen von
wirtschaftlich interessanten sulfidischen Vererzungen geeignet ist. Ferner konnten sie die
Korngröße von Erzmineralen ableiten.
Ein Problem das sich bei SIP-Messungen stellt, ist die elektromagnetische Kopplung
zwischen den stromführenden Kabeln und dem Erdboden. Bei hohen Frequenzen (ab etwa
40 Hz) kommt es zu einer Wechselwirkung zwischen den Kabeln und dem Untergrund, die
mit der Größe der Auslage zunimmt. Hierdurch wird ein elektrisches Feld induziert, welches
das eigentliche SIP-Signal überlagert. In der Praxis sind große Auslagen notwendig, um große
Eindringtiefen zu erreichen. Eine Beschränkung auf niedrige Frequenzen ist ebenfalls nicht
wünschenswert, weil der Mehrgewinn an Informationen bei der SIP im Gegensatz zur
klassischen IP auf der Untersuchung der spektralen Eigenschaften des Untergrunds basiert.
Zur
Bewältigung
dieses
Problems
gab
es
eine
Reihe
von
Ansätzen,
Kabelkopplungseffekte nachträglich aus den Daten zu korrigieren [Hallof, 1974], [Zonge und
Wynn, 1975], [Song, 1984]. Dabei wurde die Kopplung geschätzt, wodurch allerdings die
Gefahr entsteht, die SIP-Daten zu verfälschen.
Ein anderer Ansatz war die Berücksichtigung der Kabelkopplungseffekte bei der
Auswertung der Daten, da sie ebenfalls Untergrundinformationen beinhalten. Man kam
jedoch nicht über einen Ansatz hinaus, da die analytische Berechnung dieser Effekte extrem
rechen- und damit zeitaufwändig ist und sich als nicht praktikabel erwiesen hat [Kretzschmar,
2001].
Der im Rahmen dieser Arbeit verfolgte Ansatz zur Korrektur der SIP-Daten basiert auf
einer numerischen Simulation der induktiven Kopplungseffekte, um sie von den Messdaten
abzuziehen. Dazu wird das Programm IP3C verwendet, das von Prof. Peter Weidelt und Dr.
Volker Rath 1994 entwickelt wurde 1 , welches die Simulationen unter Berücksichtigung der
1
Persönliche Mitteilung von Dr. Volker Rath, Applied Geophysics and Geothermal Energy, E.ON
Energy Research Center, RWTH Aachen University
Einleitung
3
Untergrundbeschaffenheit, der Auslagengeometrie, sowie des verwendeten Frequenzspektrums erlaubt.
Für die vorliegende Arbeit wurden mit dem Programm IP3C eine Reihe von
Sensitivitätsstudien durchgeführt (Kapitel 3). In mehreren Feldmessungen wurden zudem
SIP-Daten
aufgenommen
und
ausgewertet.
Durch
Simulation
der
induktiven
Kopplungseffekte für diese speziellen Fälle wurde dann eine Korrektur der Daten
vorgenommen (Kapitel 4).
Theorie
4
2 Theorie
2.1 Der IP-Effekt
Bei geoelektrischen Messungen mit der Vierpunkt-Methode wird Strom über zwei
Elektroden in den Untergrund eingespeist. An zwei weiteren Elektroden wird das Potential
gemessen, um aus Strom und Potentialdifferenz den Widerstand des Erdbodens zu berechnen.
Schaltet man den Strom ab, so fällt die Spannung nicht direkt auf Null, sondern
zunächst auf einen Restwert und klingt dann langsam ab. Beim Einschalten des Stroms tritt
der umgekehrte Effekt auf: Die Spannung springt auf einen Teilwert der Maximalspannung
und erreicht diese erst nach einiger Zeit. Der Erdboden verhält sich also wie ein Kondensator.
Um die Ursache des IP-Effekts zu verstehen, muss man die elektrischen
Leitfähigkeitsmechanismen im Untergrund betrachten. Man unterscheidet die elektrolytische
(an Ionen gebundene) und die metallische (an Elektronen gebundene) Leitung. Bei
elektrolytischer Leitung liegt die Ursache des IP-Effekts in der Membranpolarisation,
während bei metallischer Leitung die Ursache die Elektrodenpolarisation ist [Kretzschmar,
2001].
2.2 Membranpolarisation
Die Membranpolarisation ist die Schwächere der beiden Polarisationsarten. Ihre IPEffekte sind etwa um eine Größenordnung kleiner als die durch Elektrodenpolarisation
hervorgerufenen.
Ursache der Membranpolarisation ist die elektrische Doppelschicht (EDL, engl.
Electrical Double Layer). Sie führt in einer mit einem Elektrolyt gefüllten Pore zu einer
unterschiedlichen Mobilität von Kationen und Anionen. Bevorzugt tritt dies in kleinen Poren
(auch aktive Zonen genannt) auf oder in der Nähe von Mineralen mit unausgeglichener
Ladungsbilanz (z.B. Tone), während sich die Ionen in großen Poren (passive Zonen) relativ
frei bewegen können. Aufgrund der negativen Oberflächenladung vieler Gesteinsminerale
werden die Anionen aus kleinen Poren verdrängt. Es bildet sich eine positive Ladungswolke
im Elektrolyt. Für die ohnehin größeren Anionen bedeutet dies, dass ihre Mobilität aufgrund
der als Barrieren dienenden Ladungswolken weiter eingeschränkt wird (Abbildung 1 links).
Theorie
5
I
I
E=0
E≠0
Abbildung 1: Porenverengung ohne angelegtes E-Feld (links) und mit angelegtem E-Feld (rechts) [nach
Klitzsch, 2004].
Legt man ein äußeres elektrisches Feld an, gerät das System aus dem Gleichgewicht.
Daraufhin streben die Ladungsträger einen neuen Gleichgewichtszustand an, was zu einer
Anhäufung von Anionen in der Nähe der positiven Ladungswolken führt. Kationen können
diese positiven Ladungswolken überwinden, weil sie durch ihre ebenfalls positive Ladung
von ihnen abgestoßen werden, während Anionen von den positiven Ladungswolken
angezogen und damit blockiert werden (Abbildung 1 rechts). Der Name Membranpolarisation
ist also durch die Membranwirkung der positiven Ladungswolke begründet. An diesen auch
aktive Zonen genannten Stellen entsteht ein Kationenüberschuss, der makroskopisch als
Polarisation messbar ist. Die Membranpolaristion ist also von der Porengeometrie abhängig.
Bei Abschalten des äußeren elektrischen Feldes klingt die Polarisation langsam durch
Diffusion ab. Wird Wechselstrom zur Erzeugung des elektrischen Feldes verwendet, so
entspricht die Membranpolarisation dem Auf- und Entladevorgang eines Kondensators.
Die makroskopisch messbare Polarisation zeigt eine Frequenzabhängigkeit. Bei
kleinen Frequenzen bleibt genügend Zeit, die Polarisation auszubilden, während bei höheren
Frequenzen kein Gleichgewichtszustand mehr erreicht werden kann. Als Folge dessen werden
bei höheren Frequenzen kleinere spezifische Widerstände gemessen [Radic, 1997].
2.3 Elektrodenpolarisation
Die Gesteinsmatrix wird hier als nichtleitend betrachtet. Die leitenden Eigenschaften
erhält das Gestein durch einen Elektrolyten, der sich in Poren und Klüften befindet. Diese
Theorie
6
Poren und Klüfte können von Erzpartikeln blockiert werden. Ist dies der Fall, so entsteht ein
Phasenübergang zwischen Elektrolyt und metallischem Leiter. Durch elektrochemische
Austauschreaktionen bildet sich im Metall eine Schicht freier Elektronen [Militzer und
Weber, 1985], der eine diffuse Zone positiver Ionen im Elektrolyt entgegensteht (Abbildung 2
oben). Ohne weitere äußere Einflüsse ist das System im Gleichgewicht. Es bildet sich eine
elektrische Doppelschicht [Radic, 1997].
Gesteinsmatrix
Elektrolyt
Erzmineralkorn
E=0
Sternschicht
diffuse Schicht
Gesteinsmatrix
Elektrolyt
-
+
Erzmineralkorn
E
Sternschicht
diffuse Schicht
Abbildung 2: Elektronenleitendes Mineralkorn ohne angelegtes E-Feld (oben) und mit angelegtem E-Feld
(unten).
Wird von außen ein elektrisches Feld angelegt, polarisiert sich das Erzpartikel und
wird zu einem elektrischen Dipol. Dadurch verformt sich die ihn umgebende Ladungswolke
Theorie
7
aus positiven Ionen, das System gerät aus dem Gleichgewicht. Als Folge wird ein neuer
Gleichgewichtszustand gesucht (Abbildung 2 unten).
Bei einem zeitlich veränderlichen elektrischen Feld muss man drei Frequenzbereiche
unterscheiden. Verändert sich das Feld langsam, so können die Ladungsträger den
Veränderungen folgen und jederzeit im Gleichgewicht sein. Man beobachtet in diesem Fall
ausschließlich Ohmsche Leitfähigkeit.
Erhöht man die Frequenz des elektrischen Feldes, so wirkt sich die Trägheit der Ionen
aus:
Sie
reagieren
zeitverzögert
auf
die
Veränderungen
des
Feldes,
was
zu
Relaxationserscheinungen und damit zu einer Polarisation führt. Es kommt zu einer
Phasenverschiebung
zwischen
Strom
und
Spannung.
Das
Stromsignal
eilt
dem
Spannungssignal voraus. Der Widerstand wird komplex.
Wird die Frequenz weiter erhöht, wird der Widerstand wieder reell und damit ein
Ohmscher Widerstand. Die Feldveränderungen sind nun so schnell, dass die Ionen aufgrund
ihrer Trägheit dem äußeren Feld nicht folgen können [Kretzschmar, 2001].
Generell verhält sich eine von einem Erzpartikel blockierte Gesteinspore analog einem
verlustbehafteten Kondensator. Das Partikel verhindert den direkten Ladungstransport. Nur
durch Austauschreaktionen an der Phasengrenze zwischen Elektrolyt und Metalloberfläche ist
Ladungstransport möglich. Dabei unterscheidet man zwei Mechanismen: Reduktion und
Oxidation. Nimmt ein Kation im Elektrolyt ein freies Elektron aus der Metalloberfläche auf,
so spricht man von Reduktion.
Bei Oxidation gibt ein Metallatom ein Elektron ab, ionisiert und kann nun als Kation
in Lösung gehen. Liegt ein äußeres elektrisches Feld an, das das Gleichgewicht stört, so
kommt es zu einem Nettoladungstransport über Strecken, die weiter sind, als die Dimensionen
des Systems Metall-Ladungswolke. Dabei werden an der Phasengrenze Kationen aus dem
Elektrolyt herausgeführt und es bildet sich eine Verarmungszone. Der Ladungstransport ist
dann ein Diffusionsprozess [Wong, 1979].
Theorie
8
2.4 Messungen
Wie bei anderen geoelektrischen Verfahren gibt es eine Vielzahl möglicher
Messaufbauten. Allen gemein ist, dass Strom über zwei Elektrodenspieße in den Untergrund
eingespeist wird, und an zwei anderen Elektroden die Spannung gemessen wird. Man spricht
von einer Vierpunktanordnung. In den Feldmessungen für diese Arbeit wurden ausschließlich
Dipol-Dipol-Auslagen verwendet, bei denen Strom- und Spannungselektroden in jeweils
gleichem Abstand voneinander angeordnet sind und sich lediglich der Abstand zwischen den
beiden Dipolen um ganzzahlige Elektrodenabstände verändert, wie in Abbildung 3 dargestellt.
I
a
U
na
a
Abbildung 3: Schematische Darstellung einer Dipol-Dipol-Auslage.
IP-Messungen können im Zeit- und Frequenzbereich durchgeführt werden. Trägt man
Strom und Spannung über der Zeit auf, so erkennt man im Spannungsdiagramm, wie bei
Einschalten des Stroms die Spannung nicht sofort ihren Maximalwert erreicht sondern
zunächst nur einen Teil davon. Analog geht die Spannung bei Abschalten des Stroms nicht
sofort auf Null, sondern erst nach einer endlichen Zeit t (Abbildung 4). Grund dafür sind
elektromagnetische Felder, die durch das schnelle Abschalten induziert werden und der
Spannungsabnahme entgegenwirken [Blaschek, 2006].
Theorie
Strom
9
Ip
Spannung
Zeit
V0
Vp
Vs
Zeit
Abbildung 4: Strom- und Spannungssignal im Zeitbereich. V0 bezeichnet die sprunghaft erreichte
Spannung beim Einschalten, Vs den Restwert der Spannung nach Abschalten des Stroms. Vp bezeichnet
die Maximalspannung [nach Kretzschmar, 2001].
Aus dem Verhältnis der Spannung Vs, die unmittelbar nach dem Abschalten des
Stroms erreicht wird, und der Maximalspannung Vp kann die Aufladefähigkeit berechnet.
Gebräuchlich sind dafür zwei verschiedene Definitionen [Radic, 1997]:
m=
und
Vs
Vp
(2.1)
Theorie
10
∞
1
M=
⋅ V (t )dt .
V p ∫0
(2.2)
Bei Feldmessungen bergen beide Ansätze Unsicherheiten. So ist die Bestimmung von
Vs in der Praxis problematisch, weil unmittelbar nach dem Abschalten des Stroms
elektromagnetische Effekte das IP-Signal überlagern [Radic, 1997]. Bei der Integration
besteht das Problem, dass der Lade- bzw. der Entladevorgang nicht unendlich lange andauern.
Außerdem kann das Signal nicht zeitlich kontinuierlich aufgezeichnet werden, sondern nur zu
diskreten Zeitpunkten, wodurch ebenfalls Ungenauigkeiten auftreten [Blaschek, 2006].
Aus diesem Grund wird die Spannung zu verschiedenen Zeiten t0 bis tn gemessen.
Dabei sind die Zeitintervalle ti+1 – ti nicht äquidistant, so dass ihr gegenseitiger Abstand
berücksichtigt werden muss. Es ergibt sich:
t
i +1
1 n
1
m=
⋅∑
⋅ ∫ V (t )dt .
V p i =0 t i +1 − t i ti
(2.3)
Obwohl die Größen m und M nicht äquivalent sind, werden beide häufig als
„Aufladbarkeit“ bezeichnet. Genauer ist es, von der Aufladbarkeit m zu sprechen, während M
eine der gespeicherten Energie proportionale Größe ist [Radic, 1997].
Misst man im Frequenzbereich, so speist man Wechselstrom zweier verschiedener
Frequenzen f1 und f2 im Abstand von mindestens einer Dekade in den Untergrund ein. Der IPEffekt zeigt sich hier in einer Verringerung des Spannungsmaximums bei höheren
Frequenzen (Abbildung 5). Es gilt f1 > f 2 ⇒ V1 < V2 .
Aus diesen Spannungsmaxima berechnet man den Frequenzeffekt FE:
FE =
V2 − V1
.
V1
(2.4)
Ist der Strom I in der ersten Messung nahe am Gleichstromfall und in der zweiten
Messung im Idealfall ein unendlich hochfrequenter Wechselstrom, so gibt der Frequenzeffekt
FE die relative Differenz zwischen den scheinbaren spezifischen Widerständen ρf→0 und ρf→∞
an:
Theorie
11
FE =
Zwischen
Frequenzeffekt
ρ f →0 − ρ f →∞
.
ρ f →∞
FE
und
Aufladefähigkeit
(2.5)
m
besteht
ein
enger
Zusammenhang. Bei Einschalten des Stroms gilt [Blaschek, 2006], [Telford et al., 1990]:
lim V (t ) ∝ ρ f →0
t →∞
lim V (t ) ∝ ρ f →∞ .
und
(2.6)
t →0
Damit gilt:
m=
V (t ) − limV (t ) ρ f →0 − ρ f →∞
Vs lim
FE
t →0
=
=
= t →∞
.
Vp
limV (t )
ρ f →0
FE + 1
(2.7)
t →∞
Stellt man nach FE um, so ergibt sich (vergleiche Anhang A.1):
FE =
Strom
f1
I1
Spannung
V1
m
.
1− m
Strom
Zeit
f1
(2.8)
I2
Spannung
Zeit
f2
Zeit
f2
V2
Abbildung 5: Strom- und Spannungssignal im Frequenzbereich [nach Kretzschmar, 2001].
Zeit
Theorie
12
Theoretisch sind die Messungen also äquivalent und können ineinander umgerechnet
werden. Bei praktischen Messungen ist das jedoch nicht möglich, da dafür einerseits über
einen
Frequenzbereich
von
f = 0 bis f = ∞ Hz
gemessen
und
andererseits
das
Abklingverhalten des Spannungssignals im Zeitbereich vollständig erfasst werden müsste
[Blaschek, 2006].
2.5 Spektrale IP
Bei IP im Frequenzbereich wird bei zwei Frequenzen gemessen. Erhöht man die
Anzahl der Messfrequenzen spricht man von SIP. Trägt man Strom- und Spannungssignale
gegen die Zeit auf, so erkennt man zwei sinusförmige Signale I und U unterschiedlicher
Amplitude, die um eine Phase φ gegeneinander verschoben sind (Abbildung 6). Aus den
Werten für Strom I und Spannung U kann der Betrag |ρ| und die Phasenverschiebung φ des
scheinbaren spezifischen Widerstands ρ berechnet werden. Bei SIP-Messungen werden |ρ|
und φ häufig über dem Logarithmus der Frequenz aufgetragen, um das Widerstands- und
Phasenspektrum darzustellen (Abbildung 7). Das Widerstandspektrum zeigt typischerweise
eine Abnahme des Widerstands mit steigender Frequenz. Dabei durchläuft es einen
Wendepunkt. Der Phasenverlauf zeigt ein anderes Verhalten: Zunächst wird die Phase kleiner,
durchläuft ein Minimum, um dann wieder anzusteigen. Das Minimum liegt bei der gleichen
Frequenz wie der Wendepunkt des Widerstandsspektrums.
Theorie
13
Amplitude
Strom
I
Spannung
φ
V
Zeit
Abbildung 6: Der SIP-Effekt in der Zeitreihe. Strom und Spannung sind um die Phase φ verschoben [nach
Kretzschmar, 2001].
Betrag |ρ|
Frequenz
Phase φ
Abbildung 7: Theoretische Amplituden- und Phasenspektren des scheinbaren Widerstands bei SIPMessungen. Die Punkte bezeichnen den Wendepunkt bzw. das Minimum des Amplituden- bzw.
Phasenspektrums [nach Kretzschmar, 2001].
Die Spektren variieren in Abhängigkeit von der inneren Gesteinsstruktur und gestatten
Rückschlüsse auf die spezifische Beschaffenheit des Untergrunds. Man erhält im Vergleich zu
einfachen IP Messungen zusätzliche Informationen [Kretzschmar, 2001].
Theorie
14
2.6 Relaxationsmodelle
Um die an Gesteinen gemessenen Spektren zu erklären, kann man Ersatzschaltbilder
verwenden [Wong, 1979]. Dafür gibt es eine Reihe von Modellen, wobei für die vorliegende
Arbeit vor allem das Cole-Cole-Modell [Cole und Cole, 1941] von Interesse ist.
2.6.1 Cole-Cole-Modell
Die Polarisation im Untergrund verhält sich ähnlich dem Auf- und Entladeprozess
eines Kondensators. Das Cole-Cole-Modell führt eine Parallelschaltung ein, bestehend aus
Ohmschem Widerstand R0 und einem Ohmschen Widerstand R1, der mit einem Element
kontanter Phase (CPE, engl. Constant Phase Element) in Reihe geschaltet ist [Cole und Cole,
1941], wie in Abbildung 8 dargestellt.
R0
R1
(iωX )−c
Abbildung 8: Ersatzschaltbild des Cole-Cole Modells. R0 bezeichnet den Ohmschen Widerstand des
Untergrunds, R1 + (iωX)-c das Äquivalent eines verlustbehafteten Kondensators und c den
Frequenzexponenten [nach Kretzschmar, 2001].
Theorie
15
Damit ergibt sich für die Gesamtimpedanz Z(ω):
1
1
1
=
+
.
Z (ω ) R0 R1 + (iωX ) −c
(2.9)
Ersetzt man:
R0
m :=
R0 + R1
und
⎛R ⎞
τ := X ⎜ 0 ⎟
⎝m⎠
1
c
= X (R0 + R1 ) c ,
1
(2.10)
dann folgt daraus (vergleiche Anhang A.2):
⎛
⎛
1
Z (ω ) = R0 ⎜1 − m⎜⎜1 −
c
⎜
⎝ 1 + (iωτ )
⎝
⎞⎞
⎟⎟ .
⎟⎟
⎠⎠
(2.11)
Dabei ist m die Aufladbarkeit, R0 der Gleichstromwiderstand, τ die Zeitkonstante des
Relaxationsprozesses, c den Frequenzexponenten und ω die Frequenz des Wechselstroms.
Die folgenden Grenzwertbetrachtungen ergeben:
1) ω → 0 : ⇒ Z (ω = 0) = R0 .
2) ω → ∞ : ⇒ Z (ω = ∞) =
R0 ⋅ R1
.
R0 + R1
(2.12)
Für 1) sperrt der Kondensatoranteil (iωX)-c und es bleibt lediglich der Ohmsche
Widerstand R0 übrig. In Fall 2) verschwindet der Imaginärteil von Z(ω), der Widerstand wird
reell [Blaschek, 2006].
2.7 Kabelkopplungseffekte
Bei SIP-Messungen ist es wünschenswert, das Frequenzspektrum über 6 Dekaden
(1 mHz bis 1 kHz) zu erfassen, um die spektrale Information hinsichtlich der
Gesteinseigenschaften interpretieren zu können. Ferner ist bei Feldmessungen die
Auslagenweite von Bedeutung, da von ihr die Eindringtiefe in den Untergrund abhängt. Dabei
Theorie
16
gilt, dass die Eindringtiefe ungefähr ein Viertel der Auslagenweite beträgt. Das bedeutet, dass
die in der Praxis benötigten Auslagen (z.B. zur Erkundung von Altlasten oder zur
Erzexploration) sehr groß werden können.
Beide Aspekte, sowohl das Frequenzintervall, als auch die Auslagenweite, stellen
jedoch ein Problem bei der Durchführung von SIP-Messungen dar. Aufgrund der zwischen
den Elektroden verlaufenden Kabel kommt es zu elektromagnetischen Kopplungseffekten.
Dabei unterscheidet man zwischen kapazitiver und induktiver Kopplung. Diese Effekte
nehmen bei steigender Frequenz und Auslagenweite zu und überlagern das eigentliche SIPSignal.
2.7.1 Kapazitive Kabelkopplung
Kapazität ist ein Maß der Proportionalität zwischen elektrischer Ladung q und dem
entsprechenden Potential V: q = C ⋅ V [Gerthsen et al., 1986].
Unter kapazitiver Kopplung versteht man die Wechselwirkung zweier isolierter
elektrischer Leiter über elektrische Felder [Althaus, 2003]. Bei SIP-Messungen tritt kapazitive
Kopplung ungewollt zwischen den Kabeln und dem Erdboden auf. Die verwendeten Kabel
sind zwar isoliert, jedoch verhindert die Isolierung nur im Gleichstromfall vollständig das
Abfließen von Strom in den Boden. Fließt Wechselstrom durch die Kabel, so stellt die
Isolierung eine Kapazität zum Erdboden dar, vergleichbar einem Kondensator mit
Dielektrikum. Darüber fließt Strom in den Untergrund ab. Die Kapazität zwischen Kabel und
Boden wurde von Madden und Cantwell [1968] mit C K = 1,6 ⋅10 −5 μF/m Kabellänge l
geschätzt. Daraus ergibt sich für die Impedanz Zcc zwischen Kabel und Boden:
Z cc =
1
.
iω ⋅ C K ⋅ l
(2.13)
Dabei ist ω die Kreisfrequenz.
Eine elektrische Ladung q erzeugt in Materie mit der Dielektrizitätskonstanten ε r ⋅ ε 0
ein elektrisches Feld E:
Theorie
17
G G
E (r ) =
G G
r − r0
q
.
4π ⋅ ε r ε 0 rG − rG0 3
(2.14)
G
G
Dabei ist r der Ortsvektor und r0 der Ursprungsvektor. ε r und ε 0 bezeichnen
relative Dielektrizitätskonstante und Dielektrizitätskonstante des Vakuums.
Es gilt die Beziehung [Tipler, 1994]:
G G
G
E (r ) = −∇V (r ) .
(2.15)
Daraus folgt:
G
V (r ) =
q
1
G G .
4π ⋅ ε r ε 0 r − r0
(2.16)
Nach dem Superpositionsprinzip folgt für mehrere Ladungen qi:
G
V (r ) =
1
4π ⋅ ε r ε 0
qi
∑ rG − rG
i
.
(2.17)
0
Bei SIP-Messungen fließt Wechselstrom durch die Kabel. Es gilt:
I (t ) =
d
d
q (t ) = q0 e iωt = iωq (t )
dt
dt
I (t )
⇒ q(t ) = −i ⋅
.
ω
(2.18)
Theorie
18
y
T
0
Erdoberfläche
r
R
z
x
εErde
Abbildung 9: Schematische Darstellung einer Ladung q am Punkt T, die eine Potentialverteilung im
Untergrund erzeugt.
Wir betrachten eine zeitliche veränderliche Ladung q, die am Punkt T auf der
Erdoberfläche liegt und möchten die Potentialverteilung an einem beliebigen Punkt R im
Untergrund bestimmen (Abbildung 9). Das von der Ladung q verursachte elektrische Feld
wird in der Erde durch Polarisationsvorgänge abgeschwächt [Althaus, 2003]. Die
Potentialverteilung im Untergrund ergibt sich nach Jackson [1975]:
V (t ) =
I (t ) 1
.
2πσ r
(2.19)
Dabei ist σ die elektrische Leitfähigkeit des Untergrunds.
R2
R1
R
C
Abbildung 10: Ersatzschaltbild für die kapazitive Kopplung: Strom fließt sowohl über die Elektroden
(mit den Übergangswiderständen R1 und R2) in den Boden (Widerstand R), als auch über kapazitive
Kopplung.
Zur Berechnung des durch kapazitive Kopplung in die Erde fließenden Stroms IC(t)
wird ein Ersatzschaltbild für ein zwischen zwei Elektroden auf dem Boden liegendes Kabel
erstellt (Abbildung 10). Es besteht aus den Ankopplungswiderständen R1 und R2 der
Theorie
19
Elektroden, die in Reihe geschaltet sind mit dem Widerstand R des Untergrunds. Dazu
parallel geschaltet ist die Kapazität des Kabels C. Der Gesamtstrom Iges berechnet sich aus
den Einzelströmen IR und IC:
IR =
U 0 ⋅ cos(ωt )
.
Rges
I C = U 0 ⋅ cos(ωt ) ⋅ iωC .
(2.20)
U0 bezeichnet die angelegte Spannung, Rges die Summe der Einzelwiderstände R1, R2
und R. Damit wird das durch den kapazitiven Anteil erzeugte Potential Vc(t,r):
Vc (t , r ) =
U 0 ⋅ cos(ωt ) iωC
.
2πσ
r
(2.21)
Das gilt für eine Ladung q, die auf der Oberfläche liegt.
Im Falle eines auf dem Boden liegenden Kabels wird über die Einzelladungen qi
aufaddiert:
Vges (t , r ) =
U 0 ⋅ cos(ωt ) ⋅ iωC N 1
⋅∑ .
2πσ
i =1 ri
(2.22)
Dabei ist N die Gesamtanzahl der Ladungen im Kabel. Über der Länge des Kabels von
10 m ändert sich die Spannung aufgrund der sehr großen Wellenlängen von λ = 300 km bei
einer Frequenz des Wechselstroms von 1 kHz bis λ = 300000000 km bei 1 mHz nicht
signifikant.
Theorie
20
2.7.2 Induktive Kabelkopplung
Leiter
Strom
Magnetfeld
Abbildung 11: Magnetfeld eines stromdurchflossenen Leiters.
Wird ein auf dem Boden liegendes Kabel von Wechselstrom durchflossen, so wird
durch das zeitlich variierende elektrische Feld ein Magnetfeld erzeugt, dessen Ausrichtung
spiralförmig um das Kabel verläuft (Abbildung 11). Dieses magnetische Feld wiederum
induziert im Untergrund ein elektrisches Feld, welches sich dem galvanisch angekoppelten
überlagert. Man misst eine Potentialdifferenz, die durch das resultierende Feld erzeugt wird,
und erhält somit durch induktive Kopplung verfälschte Widerstands- und Phasenwerte.
Induktive Kabelkopplungseffekte führen zu einer signifikanten Verfälschung der Phase, wenn
die Frequenz des Wechselstroms über etwa 50 Hz liegt. Außerdem nehmen die induktiven
Effekte mit größer werdenden Auslagen zu.
Um das von einem horizontalen Kabel induzierte elektrische Feld zu bestimmen,
betrachtet man das Kabel als Aneinanderreihung einer Vielzahl einzelner Dipole, über die
man integriert.
Für ein Kabel in x-Richtung (z-Achse weist in die Tiefe) ist das elektrische Feld Ex
eines Dipols in x-Richtung [Ward und Hohmann, 1988]:
Ex =
∞
⎤
Ids ∂ 2 ⎡
(1 −r TM ) u0 − (1 + rTE ) iωμ 0 ⎥ 1 J 0 (λρ )dλ
2 ∫⎢
u0 ⎦ λ
iωε 0
4π ∂x 0 ⎣
∞
iωμ 0 Ids
(1 + rTE ) λ J 0 (λρ )dλ .
−
∫
u0
4π 0
(2.23)
Theorie
21
Dabei ist I der Strom, der durch das Dipolelement der Länge ds fließt, rTM und rTE der
transversal
magnetische
bzw.
transversal
elektrische
Reflektionskoeffizient,
u 0 = λ2 − ω 2 μ 0ε 0 , ρ der spezifische Widerstand und λ die Integrationsvariable. Die
Reflektionskoeffizienten hängen vom komplexwertigen Widerstand des geschichteten
Untergrunds ab. J0 bezeichnet die Besselfunktion erster Art und Ordnung Null:
∞
(− 1)r ⎛⎜ λρ ⎞⎟
2r
⎝ 2 ⎠ .
Γ((r + 1)r!)
(2.24)
Γ((r + 1)r!) = ∫ t (r +1)r!−1e −t dt .
(2.25)
J 0 (λρ ) = ∑
r =0
Dabei ist die Gammafunktion Γ:
∞
0
y
na
a
dS
0
r1
r2
a
ds
r3
r4
Erdoberfläche
x
r
σ(z)
z
Abbildung 12: Schema einer Dipol-Dipol Auslage über polarisierbarem Untergrund [nach Caglar, 2000].
Betrachtet man nun ein Kabel der Länge r2-r1 entlang der x-Achse, so ergibt sich für
das elektrische Feld an der Oberfläche eines geschichteten Halbraums
r
⎡ r2
∂Q( R) 2 ⎤
E x = I ⎢ ∫ P( R)dS +
⎥.
∂x r1 ⎥⎦
⎢⎣ r1
(2.26)
Theorie
22
Dabei ist
P( R) =
iωμ 0 I
4π
∞
λ
∫ (1 + r ) u J (λR )dλ
0
TE
(2.27)
0
0
und
∞
u0
iωμ 0 ⎤
∂Q( R)
I x ⎡
(
)
(
)
=−
−
−
+
1
r
1
r
TM
TE
⎢
⎥ J 1 (λR )dλ .
∂x
iωε 0
u0 ⎦
4π R ∫0 ⎣
(2.28)
J1 bezeichnet die Besselfunktion erster Art und Ordnung 1, R = x − x' und es gilt:
d
J 0 (λ x ) = − λ ⋅ J 1 ( λ x ) .
dx
(2.29)
Die Integration des elektrischen Feldes zwischen den Potentialelektroden r3 und r4
führt dann zur gemessenen Spannung V:
⎡ r4 r2
⎤
V = I ⎢ ∫ ∫ P(R )dSds + Q(r4 − r2 ) − Q(r4 − r1 ) − Q(r3 − r2 ) + Q(r3 − r1 )⎥ .
⎢⎣ r3 r1
⎥⎦
(2.30)
Hierbei ist
Q( R) =
∞
u0
iωμ 0 ⎤ 1
I ⎡
− (1 + rTE )
⎢(1 − rTM )
⎥ J 0 (λR)dλ .
∫
4π 0 ⎣
iωε 0
u0 ⎦ λ
(2.31)
Mit Z = V I folgt für die Impedanz Z [Ward und Hohmann, 1988]:
r4 r2
⇒ Z = ∫ ∫ P(r2 − r1 )dSds + Q(r4 − r2 ) − Q(r4 − r1 ) − Q(r3 − r2 ) + Q(r3 − r1 ) .
r3 r1
(2.32)
Theorie
23
Daraus kann nun die Phase φ berechnet werden:
Z = Z e iφ
⎛ Im[Z ] ⎞
⇒ φ = arctan⎜⎜
⎟⎟ .
⎝ Re[Z ] ⎠
(2.33)
Bei einer Dipol-Dipol-Anordnung, wie in Abbildung 12, mit Elektrodenabstand a und
Dipolabstand na gilt für die Abstände:
r4 − r2 = (n + 1)a ,
r4 − r1 = (n + 2)a ,
r3 − r2 = na ,
(2.34)
r3 − r1 = (n + 1)a ,
r2 − r1 = a .
Die Reflektionskoeffizienten rTE und rTM verschwinden für den Fall, dass über einem
homogenen Halbraum gemessen wird. Die Terme für P(R) und Q(R) in den Gleichungen 2.27
und 2.31 vereinfachen sich zu:
P( R) =
iωμ 0 I
4π
∞
λ
∫u
0
J 0 (λR)dλ
(2.35)
0
und
∞
iωμ 0 ⎤ 1
I ⎡ u0
Q( R) =
−
⎢
⎥ J 0 (λR)dλ .
∫
4π 0 ⎣ iωε 0
u0 ⎦ λ
(2.36)
Daraus folgt für Q(R) (vergleiche Anhang A.3):
I
Q( R) =
4π ⋅ iωε 0
∞
λ
0
0
∫u
J 0 ( λ R ) dλ .
(2.37)
Theorie
24
Setzt man die Gleichungen 2.35 und 2.37 in die Gleichung 2.32 ein, so erhält man für
die Impendanz Z:
Z=
iωμ 0 I
4π
r4 r2 ∞
λ
r3 r1 0
0
∫∫∫u
J 0 (λ (r2 − r1 )dλdsdS
∞
I
λ
(J 0 (λ (r4 − r2 )) − J 0 (λ (r4 − r1 )) − J 0 (λ (r3 − r2 )) + J 0 (λ (r3 − r1 ) )dλ .
+
∫
4π ⋅ iωε 0 0 u 0
Für
Dipol-Dipol-Anordnungen
ergibt
das
unter
Berücksichtigung
(2.38)
der
Gleichungen 2.34:
Z=
iωμ 0 I
4π
r4 r2 ∞
λ
r3 r1 0
0
∫ ∫∫ u
∞
J 0 (aλ )dλdsdS
I
λ
(2 ⋅ J 0 ((n + 1)aλ ) − J 0 ((n + 2)aλ ) − J 0 (naλ ) )dλ .
+
∫
4π ⋅ iωε 0 0 u 0
(2.39)
Theorie
25
2.8 Das Messgerät SIP256C
Die SIP-Messungen im Rahmen dieser Arbeit wurden mit der Apparatur SIP256C der
Firma Radic-Research durchgeführt.
Das Gerät besteht aus einer Basisstation und zwanzig Mobilstationen. Um eine
Messung vorzunehmen, wird zunächst eine Auslage definiert, wobei Elektroden entlang eines
Maßbandes in einem bestimmten Abstand zueinander in den Boden gesteckt werden. Jede
dieser Elektroden wird daraufhin mit einer Mobilstation verbunden, über die sie mit Strom
versorgt werden kann. Jede Elektrode kann sowohl zur Stromeinspeisung, als auch zur
Potentialmessung verwendet werden. Die Strom- und Spannungsmessungen erfolgen in der
Mobilstation. Die Mobilstationen werden untereinander mit Glasfaserkabeln verbunden,
wobei die erste Mobilstation an die Basisstation angeschlossen wird. Ein Laptop wird mit der
Basisstation verbunden, um sie zu steuern. Im Messbetrieb geschieht das über ein Programm,
mit dem man die Messung konfigurieren und überwachen kann. Die Basisstation spricht
daraufhin die Mobilstationen an und die Messung wird bei allen in einer Steuerungsdatei
bestimmten Elektrodenkonfigurationen und Frequenzen durchgeführt. Zur Stromversorgung
wird die Basisstation an eine 12 V Batterie angeschlossen. Sie versorgt die Stromelektroden
dann mit einem Wechselstrom, dessen Spannung manuell eingestellt werden kann.
Bei der Messung werden die Widerstands- und Phasenspektren für die einzelnen
Elektrodenkonfigurationen aufgenommen. Zusätzlich können die Daten in einer PseudoTiefensektion grafisch dargestellt werden.
Kopplungseffekte zwischen Strom-
und
Potentialkabeln werden durch die
Verwendung optischer Fasern für die Datenübertragung zur Basisstation und durch die direkte
Messung der Potentiale an den Stromelektroden vermieden.
Die induktive und kapazitive Kopplung zwischen Stromkabel und Boden wird
minimiert, indem an beiden Stromelektroden ein Sinussignal anliegt, wobei das eine Signal
gegenüber dem anderen um 180° phasenverschoben ist. Daraus folgt, dass nur das Kabel
zwischen den Elektroden koppeln kann, da der Teil des Kabels, in dem die beiden
stromführenden Drähte parallel laufen kein resultierendes Feld (nach außen) hat.
Theorie
26
2.9 Das Programm IP3C
Schwerpunkt dieser Arbeit ist die Untersuchung induktiver Kabelkopplungseffekte.
Das Ziel ist hierbei die Korrektur der aufgenommenen Spektren. Dazu werden die
auftretenden Kopplungseffekte zunächst am Computer simuliert. Prof. Dr. Peter Weidelt und
Dr. Volker Rath haben zu diesem Zweck das Programm IP3C entwickelt 2 . Es basiert auf
Fortran und erlaubt die Simulation der induktiven Kopplungseffekte über einem definierten
Untergrundmodell bei einer bestimmten Kabelauslage. Dazu wird Gleichung 2.32 numerisch
gelöst. Man kann zwischen dem Cole-Cole Modell und dem Modell der konstanten Phase
wählen. Zusätzlich lässt sich der Untergrund modellieren, indem man die Anzahl der
Schichten, ihre Mächtigkeiten, spezifischen Widerstände und Phasen angibt. Auch Anomalien
können konstruiert werden, die in ihrer Leitfähigkeit vom umliegenden Gestein abweichen.
Die Kabelanordnung lässt sich beliebig festlegen, ebenso die Geometrie der Strom- und
Potentialelektroden, sowie die Frequenzen, bei denen gemessen wird. Als Ausgabe erhält man
einen Datensatz, der für jede Elektrodenkonfiguration und Frequenz den Betrag des
Widerstands und die Phasenverschiebung ausweist. Trägt man diese Werte über der Frequenz
auf, so erhält man die simulierten Spektren. Diese können dann von den tatsächlich
gemessenen Spektren abgezogen werden, um von den Kabelkopplungseffekten bereinigte
Spektren zu erhalten. Ferner können diese bereinigten Daten invertiert werden, um korrigierte
Tiefensektionen zu erstellen.
Das vorwiegende Problem bei der Simulation der Kopplungseffekte ist die genaue
Beschreibung des Untergrunds und seiner Leitfähigkeiten. Dazu werden zunächst
Tiefensektionen aus Daten erstellt, die bei niedrigen Frequenzen aufgenommen wurden und
aus diesem Grund keine oder sehr geringe Kopplungseffekte aufweisen. Anhand dieser
Tiefensektionen kann der Untergrund in mehrere Schichten unterschiedlicher Leitfähigkeit
und Schichtmächtigkeit aufgeteilt werden. Bereiche anomaler Leitfähigkeiten werden als
Kontraste zum umgebenen Material dargestellt. Diese Informationen dienen der Modellierung
des Untergrunds, mit dem das Programm die Simulation durchführt (Abbildung 13).
2
Persönliche Mitteilung von Dr. Volker Rath, Applied Geophysics and Geothermal Energy, E.ON
Energy Research Center, RWTH Aachen University
Theorie
[ ]
0
1
27
2
3
4
5
6
7
8
-0.5
-1
-1.5
Tiefensektion des
Widerstands
(1)
Frequenzen
Geometrien
(2)
-2
ρ1
d2
ρ2
- Phase [mrad]
d1
Simulation der Phase
aufgrund induktiver (3)
Kopplung
Frequenz [Hz]
Abbildung 13: Ablauf der Berechnungen zur Korrektur der induktiven Kopplungseffekte.
Die Untergrundinformationen, die man aus den Tiefensektionen erhält, sind nicht
beliebig genau ablesbar. Mögliche Fehlerquellen sind ungenaue Schichtmächtigkeiten,
Widerstands- und Phasenwerte. Zudem erlaubt das Programm keine lateralen Veränderungen
von Widerstand und Phase, was dazu führt, dass oftmals mit Mittelwerten gearbeitet werden
muss. Zur Schätzung möglicher Fehler und des Einflusses der einzelnen Parameter auf die
Ergebnisse wurde deshalb eine Reihe von Sensitivitätsstudien durchgeführt (siehe dazu
Abschnitt 3).
Sensitivitätsstudien
28
3 Sensitivitätsstudien
3.1 Motivation
In diesem Kapitel wird der Einfluss verschiedener Parameter wie Dipolweite und
-abstand, spezifischer Widerstand des Untergrunds und Schichtmächtigkeit auf die induktiven
Kopplungseffekte untersucht, die bei SIP-Messungen mit Dipol-Dipol-Auslagen auftreten.
Zur Berechnung der induktiven Kopplungseffekte mit dem Programm IP3C muss
zunächst das Untergrundmodell spezifiziert werden. Dazu wird die Anzahl der im Untergrund
vorkommenden Schichten angegeben, deren Mächtigkeiten und die Frequenzabhängigkeit der
komplexen Widerstände (konkret die Cole-Cole Parameter bzw. die Phase beim Modell der
konstanten Phase). Im Rahmen dieser Arbeit wurde stets mit dem Modell der konstanten
Phase gearbeitet, so dass sich die Anzahl der Parameter pro Schicht auf zwei reduziert.
Die Schichtgrenzen und elektrischen Widerstände werden aus Tiefensektionen
abgeleitet und können deshalb nicht beliebig genau angegeben werden. Wie stark Variationen
der Schichtwiderstände und -mächtigkeiten die berechneten Kopplungseffekte beeinflussen,
wird
in
der
folgenden
Sensitivitätsstudie
untersucht.
Weiterhin
wird
für
die
Kopplungsberechnung von homogenen, horizontal verlaufenden Schichten ausgegangen. Eine
laterale Veränderung des Widerstands kann in IP3C durch dreidimensionale Anomalien
berücksichtigt werden.
Mit Blick auf die Untergrundsituation in den Messgebieten Inden und Kall werden
Sensitivitätsstudien für den homogenen Halbraum, sowie Zwei- und Dreischichtfälle
vorgestellt.
Die Parameter wurden so gewählt, dass sie sich im Rahmen der in der Praxis
auftretenden Fehlerrahmen und Variationen bewegen. Oft ist es schwierig, in den
Tiefensektionen die Schichtmächtigkeiten genau abzulesen. Dabei können durchaus Fehler im
Meterbereich auftreten. Bei den spezifischen Widerständen muss oftmals ein Mittelwert für
eine Schicht angenommen werden. Typische Schwankungen hierbei können bei über 100 Ωm
liegen.
Sensitivitätsstudien
29
3.2 Homogener Halbraum
Im Allgemeinen wird die Phase über dem Logarithmus der Frequenz aufgetragen.
Dadurch scheint die durch induktive Kopplung bedingte Phase exponentiell mit der Frequenz
anzusteigen (Abbildung 14 oben). Tatsächlich sind die Phasenspektren in sehr guter Nährung
linear (Abbildung 14 unten). Dies gilt für Dipol-Dipol-Anordnungen mit beliebigen
Widerständen, Dipol- und Elektrodenabständen. Wie oben erwähnt, hängt die induktive
Kopplung über homogenen Schichten neben der Frequenz im Wesentlichen von vier
Parametern ab: Schichtdicke d, spezifischer Widerstand der Schicht ρ, Elektrodenabstand a
und Dipollänge n. Geht man von einem homogenen Halbraum aus, so reduziert sich die Zahl
der Parameter auf drei.
Sensitivitätsstudien
30
ρ = 500 Ωm
a=1m
n=6
ρ = 100 Ωm
a=1m
n=6
ρ = 100 Ωm
a=5m
n=6
25
20
15
10
5
0.1
1
10
negative Phase [mrad]
30
0
1000
100
Frequenz [Hz]
25
20
15
10
5
0
200
400
600
800
1000
negative Phase [mrad]
30
ρ = 500 Ωm ρ = 100 Ωm ρ = 100 Ωm
a=1m
a=1m
a=5m
n=6
n=6
n=6
0
1200
Frequenz [Hz]
Abbildung 14: Durch induktive Kopplung verursachte Phasenspektren für den homogenen Halbraum,
dargestellt mit logarithmischer (oben) und linearer Frequenzachse (unten).
In der Praxis findet man in den häufigsten Fällen keinen homogenen, sondern einen
geschichteten Halbraum vor. Unter gewissen Bedingungen können geschichtete Halbräume
mit einem homogenen Halbraum angenähert werden. Im Folgenden soll untersucht werden,
für welche Bedingungen das gilt.
Sensitivitätsstudien
31
Bei einem Zweischichtfall existieren drei Parameter: Mächtigkeit und Widerstand der
oberen Schicht, sowie Widerstand des Halbraums. Der Widerstandskontrast zwischen den
Schichten ist besonders relevant.
Zunächst betrachten wir den Fall einer schlecht leitenden oberen und gut leitenden
unteren Schicht. Es wurde untersucht, für welche Schichtmächtigkeiten der Zweischichtfall
mit einem homogenen Halbraum angenähert werden kann. Abbildung 15 zeigt, dass für eine
dünne obere Schicht mit d1 < 0,5 m eine Betrachtung als Halbraum des Widerstands der
unteren Schicht sehr gut mit der Betrachtung als Zweischichtfall übereinstimmt. Das gilt
auch, wenn die Leitfähigkeitskontraste zwischen den Schichten größer sind (Abbildung 16).
Ist die obere Schicht sehr mächtig (d1 > 25 m), so entspricht der Zweischichtfall in guter
Übereinstimmung einem homogenen Halbraum des Widerstands der oberen Schicht, sofern
der
Leitfähigkeitskontrast
nicht
zu
groß
ist
(Abbildung
17).
Bei
großen
Leitfähigkeitskontrasten ist die Übereinstimmung nicht zufriedenstellend (Abbildung 18).
30
25
ρ1 = 500 Ωm, ρ2 = 100 Ωm
d1 = 0.1 m
d1 = 0.2 m
d1 = 0.3 m
d1 = 0.4 m
d1 = 0.5 m
hom. Halbraum
0.1
1
20
15
10
5
10
100
negative Phase [mrad]
35
0
1000
Frequenz [Hz]
Abbildung 15: Näherung des Zweischichtfalls durch den homogenen Halbraum bei dünner oberer Schicht
(d ≤ o,5 m). ρ1 und ρ2 sind die spezifischen Widerstände der beiden Schichten.
Sensitivitätsstudien
32
200
ρ1 = 500 Ωm, ρ2 = 10 Ωm
d1 = 0.1 m
d1 = 0.2 m
d1 = 0.3 m
d1 = 0.4 m
d1 = 0.5 m
hom. Halbraum
0.1
150
100
50
1
10
100
negative Phase [mrad]
250
0
1000
Frequenz [Hz]
Abbildung 16: Näherung des Zweischichtfalls durch den homogenen Halbraum bei dünner, schlecht
leitender oberer Schicht.
30
25
20
ρ1 = 100 Ωm, ρ2 = 10 Ωm
d1 = 15 m
d1 = 20 m
d1 = 25 m
hom. Halbraum
0.1
1
15
10
5
10
100
negative Phase [mrad]
35
0
1000
Frequenz [Hz]
Abbildung 17: Näherung des Zweischichtfalles durch den homogenen Halbraum bei dicker oberer Schicht
(d ≥ 15 m) mit mittlerem spezifischen Widerstand ρ1.
Sensitivitätsstudien
33
6
5
4
ρ1 = 500 Ωm, ρ2 = 10 Ωm
d1 = 15 m
d1 = 20 m
d1 = 25 m
hom. Halbraum
0.1
1
3
2
1
10
100
negative Phase [mrad]
7
0
1000
Frequenz [Hz]
Abbildung 18: Näherung des Zweischichtfalles durch den homogenen Halbraum bei dicker, schlecht
leitender oberer Schicht (d ≥ 15 m).
Ist die obere Schicht gut und die darunter liegende schlecht leitend, so ändern sich die
Bedingungen. Eine gut leitfähige obere Schicht beeinflusst die Kopplung auch dann noch
stark, wenn sie sehr dünn ist (Abbildung 19). Erst ab Schichtdicken unter 10 cm entspricht
dieser Fall einem homogenen Halbraum des Widerstands der unteren Schicht. Ist sie sehr
mächtig (d1 > 20 m), so kann der Zweischichtfall mit einem homogenen Halbraum des
Widerstands der oberen Schicht angenähert werden (Abbildung 20). Das gilt jedoch nur, falls
der Leitfähigkeitskontrast gering ist. Bei hohen Kontrasten kann in diesem Fall ein
Zweischichtfall nicht mit einem homogenen Halbraum angenähert werden (Abbildung 21 und
Abbildung 22).
Sensitivitätsstudien
34
35
30
ρ1 = 10 Ωm, ρ2 = 100 Ωm
25
d1 = 0.1 m
d1 = 0.2 m
d1 = 0.3 m
d1 = 0.4 m
d1 = 0.5 m
hom. Halbraum
0.1
20
15
10
5
1
10
100
negative Phase [mrad]
40
0
1000
Frequenz [Hz]
Abbildung 19: Näherung des Zweischichtfalls durch den homogenen Halbraum bei dünner, gut leitender
oberer Schicht.
200
150
ρ1 = 10 Ωm, ρ2 = 100 Ωm
d1 = 15 m
d1 = 20 m
d1 = 25 m
hom. Halbraum
0.1
1
100
50
10
100
negative Phase [mrad]
250
0
1000
Frequenz [Hz]
Abbildung 20: Näherung des Zweischichtfalles durch den homogenen Halbraum bei dicker, gut leitender
oberer Schicht.
Sensitivitätsstudien
35
16
14
12
ρ1 = 10 Ωm, ρ2 = 500 Ωm
10
d1 = 0.1 m
d1 = 0.2 m
d1 = 0.3 m
d1 = 0.4 m
d1 = 0.5 m
hom. Halbraum
0.1
1
8
6
4
2
10
Frequenz [Hz]
100
negative Phase [mrad]
18
0
1000
Abbildung 21: Näherung des Zweischichtfalls durch den homogenen Halbraum bei dünner, gut leitender
oberer Schicht und großem Leitfähigkeitskontrast.
200
150
ρ1 = 10 Ωm, ρ2 = 500 Ωm
d1 = 15 m
d1 = 20 m
d1 = 25 m
hom. Halbraum
0.1
1
100
50
10
Frequenz [Hz]
100
negative Phase [mrad]
250
0
1000
Abbildung 22: Näherung des Zweischichtfalles durch den homogenen Halbraum bei dicker, gut leitender
oberer Schicht und großem Leitfähigkeitskontrast.
Sensitivitätsstudien
36
Es zeigt sich, dass eine schlecht leitende obere Schicht in vielen Fällen die
Betrachtung des Systems als homogener Halbraum zulässt, unabhängig davon, ob die
Mächtigkeit der oberen Schicht klein oder groß ist. Sind die Widerstände der beiden
Schichten jedoch sehr unterschiedlich, so empfiehlt sich bei großen Schichtdicken die
Betrachtung als Zweischichtfall.
Für den Fall einer gut leitenden oberen Schicht ist die Betrachtung als homogener
Halbraum problematisch. Nur bei sehr dünnen bzw. dicken obere Schichten und nicht zu
großen Leitfähigkeitskontrasten ist das in guter Nährung möglich. Ist der Kontrast der
Widerstände zwischen den Schichten groß, so ist eine Betrachtung als homogener Halbraum
nicht möglich.
Im Folgenden soll die lineare Abhängigkeit der induktiven Kopplung von der
Frequenz näher untersucht werden. Im Gleichstromfall, findet keine induktive Kabelkopplung
statt, die Phase ist gleich Null. Kennt man die simulierte Phase bei einer höheren Frequenz, so
können alle dazwischen liegenden Phasen linear interpoliert werden. Bei den im Rahmen
dieser Arbeit durchgeführten Messungen lag die höchste Messfrequenz bei 1 kHz, weshalb
wir diese auch als Referenzwert wählen. Simuliert man die Phase für einen homogenen
Halbraum, so erhält man ein exponentielles Abklingen der negativen Phase bei 1 kHz mit
steigenden Widerständen (Abbildung 23). Führt man als weiteren Parameter den
Elektrodenabstand a ein, so erhält man für kleine Abstände flachere und für große Abstände
steilere Kurven der Form φ1kHz = ( p ⋅ a q )⋅ ρ (r ⋅a − s ) (siehe Abbildung 23), wobei p, q, r und s
Koeffizienten sind, die von der Dipollänge n abhängen.
negative Phase bei 1 kHz
Sensitivitätsstudien
37
250
n=6
200
a = 1m
a = 2m
a = 5m
150
100
50
0
0
200
400
600
800
1000
1200
Widerstand [Ωm]
Abbildung 23: Abhängigkeit der Phase bei 1 kHz φ1kHz von Widerstand ρ und Elektrodenabstand a bei
fester Dipollänge n.
Die Parameter p, q, r und s sind wiederum Funktionen der Dipollänge n. Um sie zu
bestimmen, wurden die Größen
(p ⋅ a )
q
und (r ⋅ a − s ) aus Kurven wie in Abbildung 23
bestimmt und ihrerseits über a aufgetragen (Abbildung 24). Daran werden Kurven angepasst,
aus denen die Parameter p und q (Abbildung 24 links) sowie r und s (Abbildung 24 rechts)
bestimmt werden. Das wird für verschiedene Dipollängen n wiederholt. Die einzelnen
Parameter werden dann über der Dipollänge n aufgetragen (Abbildung 25). Aus wiederum
daran angepassten Kurven können die Parameter als Funktionen von n abgelesen werden
(Gleichungen 3.1).
a [m]
2000
1500
0
(p ⋅ a )
1000
1
2
3
4
5
-0.88
q
-0.9
-0.92
500
(r ⋅ a − s )
-0.94
0
-0.96
0
1
2
3
a [m]
4
5
6
-0.98
-1
Abbildung 24: Zur Bestimmung der Parameter p, q, r und s bei fester Dipollänge n. Hier ist n = 6.
6
38
250
200
150
100
50
0
1.8
q
p
Sensitivitätsstudien
1.7
1.6
1.5
1.4
0
5
0
10
5
n
n
0.03
0.02
s
r
0.04
0.01
0
0
5
10
1.005
1.004
1.003
1.002
1.001
1
10
0
10
5
n
n
Abbildung 25: Zur Bestimmung von p, q, r und s in Abhängigkeit von n.
Für Auslagen mit a⋅n < ~40 m, wie in den Feldmessungen zu dieser Arbeit üblich,
ergibt sich:
p = 9,1351 ⋅ n1, 4203 ;
q = −0,0461 ⋅ n + 1,9055 ;
(3.1)
r = 0,0057 ⋅ n 0, 7709 ;
s = 0,9975 ⋅ n 0,0032 .
Für die negative Phase bei 1 kHz φ1kHz (in mrad) ergibt sich folgender
Zusammenhang:
φ1kHz ( ρ , a, n) = −[(9,1351 ⋅ n1, 4203 )⋅ a ( −0,0461⋅n+1,9055) ]⋅ ρ [(0,0057⋅n
und
φ0 kHz = 0 mrad .
0 , 7709
)⋅a −0,9975⋅n
0 , 0032
]
(3.2)
Sensitivitätsstudien
39
Die Phase bei Frequenzen von weniger als 1 kHz φ(f < 1 kHz) berechnet sich dann
nach:
φ( f ) =
φ1kHz
1000 Hz
⋅f
∀ f < 1 kHz .
(3.3)
Damit erhält man eine Abschätzung der induktiven Kopplung für den homogenen
Halbraum für Auslagen mit a⋅n < ~40 m. Bei größeren Auslagen würde man mit dieser
Formel zu hohe induktive Effekte berechnen, im angegebenen Gültigkeitsbereich liefert sie
jedoch gute Ergebnisse mit Abweichungen von weniger als 10 % von den mit dem Programm
IP3C simulierten Werten.
Den stärksten Einfluss in Formel 3.2 hat der Elektrodenabstand a, gefolgt von der
Dipollänge n und dem spezifischen Widerstand ρ.
Die Parameter a und n werden gewählt und können sehr genau eingestellt werden. In
der Praxis geschieht das mittels eines Maßbandes entlang dessen die Elektroden in den Boden
gesteckt werden. Der spezifische Widerstand ρ hingegen ist eine Messgröße und somit
schwieriger zu bestimmen. Es werden Messdaten bei niedrigen Frequenzen invertiert, die frei
von induktiven Kopplungseffekten sind, und Tiefensektionen erstellt. Aus diesen
Tiefensektionen wird der Widerstand des Untergrunds abgelesen und in die Simulation
eingegeben. Dadurch ist er mit einem deutlich größeren Fehler behaftet als die beiden anderen
Parameter.
3.3 Zweischichtfall
Es wurde jeweils mit einer Dipol-Dipol-Auslage gerechnet. Der Elektrodenabstand a
betrug 2 m, der Dipolabstand 36 m (n = 16). Die Phasenspektren wurden für fünf Frequenzen
zwischen 0,1 Hz und 1 kHz berechnet.
In Abbildung 26 sind die Phasenspektren für einen Untergrund bestehend aus einer
oberen Schicht mit einem spezifischen Widerstand von 10 Ωm und einem Halbraum mit
einem spezifischen Widerstand von 100 Ωm dargestellt. Die Mächtigkeit der ersten Schicht
variiert dabei zwischen 2 m und 5 m.
Man erkennt, dass die Kurven bis etwa 40 Hz nahezu übereinstimmen. Hier spielt die
induktive Kopplung keine Rolle. Erst für größere Frequenzen laufen die Kurven auseinander.
Sensitivitätsstudien
40
Bei 1 kHz führt ein Fehler in der Schichtmächtigkeit von 50 % zu einem Fehler von etwa
25 % in der Phase, verursacht durch induktive Kopplung.
In Abbildung 27 ist die Abhängigkeit der Phasenwerte vom Widerstand der ersten
Schicht dargestellt. Die Schichtmächtigkeit beträgt dabei 2 m, der Widerstand des darunter
liegenden Halbraums 1000 Ωm. Es wurden die Phasenspektren für vier Widerstände
berechnet. Es kommt dabei zu starken induktiven Kopplungseffekten, wenn der Widerstand
der oberen Schicht sehr viel kleiner ist, als jener der unteren Schicht. Beträgt der Widerstand
der oberen Schicht 1 % des Widerstands des Halbraums, so ist die Phase bei 1 kHz etwa
zehnmal höher als beim Einschichtfall (vgl. violette Kurve mit dunkelblauer Kurve in
Abbildung 27). Liegt der Widerstand der oberen Schicht über dem des Halbraums, so sind die
Effekte deutlich geringer. Hier verursacht ein zehnfach größerer Widerstand eine
Veränderung der Phase um 10 %.
Das System reagiert im Allgemeinen sensibler auf Variationen in den Parametern, je
größer die Leitfähigkeitskontraste sind.
90
80
ρ1 = 10 Ωm, ρ2 = 100 Ωm
70
60
d1 = 2 m
d1 = 2.5 m
d1 = 3 m
d1 = 5 m
50
40
30
20
10
0.1
1
10
Frequenz [Hz]
100
Abbildung 26: Zweischichtfall: Sensitivität bzgl. der Mächtigkeit der ersten Schicht.
0
1000
negative Phase [mrad]
100
Sensitivitätsstudien
41
d1 = 2 m, ρ2 = 1000 Ωm
30
ρ1 = 10 Ωm
ρ1 = 20 Ωm
ρ1 = 30 Ωm
ρ1 = 100 Ωm
ρ1 = 1000 Ωm
ρ1 = 10000 Ωm
25
20
15
10
5
0.1
1
10
Frequenz [Hz]
100
negative Phase [mrad]
35
0
1000
Abbildung 27: Zweischichtfall: Sensitivität bzgl. des Widerstands der ersten Schicht.
Der Einfluss des Widerstandes der zweiten Schicht auf die Kopplung ist in Abbildung
28 gezeigt. Die erste Schicht hat eine Dicke von 2 m und einen spezifischen Widerstand von
10 Ωm. Aufgrund der gut leitenden oberen Schicht kommt es zu großen induktiven
Kopplungseffekten, besonders, wenn auch der Halbraum gut leitend ist. In diesem Fall
erkennt man auch leichte Abweichungen vom linearen Verlauf der Spektren (Abbildung 28,
dunkelblaue Kurve bei 100 Hz. Der lineare Verlauf erscheint durch die halblogarithmische
Darstellung exponentiell ansteigend). Ab einem Widerstand der unteren Schicht von etwa
500 Ωm ändert sich die Phase nicht mehr signifikant.
Hat die obere Schicht einen Widerstand von 500 Ωm, so sind die induktiven Effekte
kleiner, jedoch nimmt die Frequenz-Sensitivität zu (Abbildung 29). Das liegt an dem größeren
Leitfähigkeitskontrast zwischen schlecht leitender oberer und gut leitender unterer Schicht. Ist
die untere Schicht ebenfalls schlecht leitend (grüne, hellblaue und violette Kurven), der
Kontrast zur oberen Schicht also klein, so sind die Effekte auf die Phase vernachlässigbar.
In Abbildung 30 ist der Widerstand der oberen Schicht 1000 Ωm. Man erkennt im
Vergleich zum vorigen Beispiel keine weitere signifikante Änderung des Phasenspektrums.
Sensitivitätsstudien
42
d1 = 2 m, ρ1 = 10 Ωm
200
ρ2 = 10 Ωm
150
ρ2 = 100 Ωm
ρ2 = 500 Ωm
100
ρ2 = 1000 Ωm
50
ρ2 = 10000 Ωm
0.1
1
10
Frequenz [Hz]
100
negative Phase [mrad]
250
0
1000
Abbildung 28: Zweischichtfall: Sensitivität bzgl. des Widerstands der zweiten Schicht bei gut leitender
erster Schicht.
160
d1 = 2 m, ρ1 = 500 Ωm
140
ρ2 = 10 Ωm
120
ρ2 = 100 Ωm
100
ρ2 = 500 Ωm
80
ρ2 = 1000 Ωm
60
ρ2 = 10000 Ωm
40
20
0.1
1
10
Frequenz [Hz]
100
negative Phase [mrad]
180
0
1000
Abbildung 29: Zweischichtfall: Sensitivität bzgl. des Widerstands der zweiten Schicht bei schlecht
leitender erster Schicht.
Sensitivitätsstudien
43
160
d1 = 2 m, ρ1 = 1000 Ωm
140
ρ2 = 10 Ωm
120
ρ2 = 100 Ωm
100
ρ2 = 500 Ωm
80
ρ2 = 1000 Ωm
60
ρ2 = 10000 Ωm
40
20
0.1
1
10
Frequenz [Hz]
100
negative Phase [mrad]
180
0
1000
Abbildung 30: Zweischichtfall: Sensitivität bzgl. des Widerstands der zweiten Schicht bei sehr schlecht
leitender oberer Schicht.
Entscheidend für die Kopplung bei einem Untergrund mit zwei Schichten sind somit
die Leitfähigkeitskontraste. Sind diese groß, reagiert die Phase empfindlich auf
Abweichungen im Widerstand der Schichten.
3.4 Dreischichtfall
Die an der RWTH Aachen genutzte SIP-Anlage SIP256C besitzt 20 Mobilstationen,
zwischen denen sich jeweils Kabel von 10 m Länge befinden. Die maximale Auslagenweite
beträgt damit 200 m. Das bedeutet, man kann den Untergrund bis zu Tiefen von etwa 50 m
erkunden. Dabei erkennt man oft mehr als nur zwei Schichten. Bei den im Rahmen dieser
Arbeit durchgeführten Messungen, die Tiefen zwischen 2 m und 10 m erkunden, handelte es
sich oft um drei Schichten, weshalb hier speziell auf diesen Fall eingegangen werden soll.
In Abbildung 31 ist eine Spektrenschar für einen Dreischichtfall dargestellt. Die
Schichtmächtigkeiten betragen jeweils 2 m, die spezifischen Widerstände der oberen und
unteren Schicht 1000 Ωm. Der spezifische Widerstand der mittleren Schicht variiert
schrittweise von 10 Ωm bis 1000 Ωm (Quasi-Einschichtfall). Die induktiven Effekte werden
von der schlecht leitenden oberen Schicht gedämpft und sind verhältnismäßig klein. Bei
Sensitivitätsstudien
44
starken Leitfähigkeitskontrasten zwischen den Schichten, reagiert die Phase empfindlich auf
Änderungen des Widerstands (Abbildung 31, rote und dunkelblaue Kurve). Die Phase ändert
sich zwischen spezifischen Widerständen von 10 Ωm und 100 Ωm etwa um das Fünffache. Ist
die zweite Schicht schlecht leitend (ρ > ~500 Ωm), der Kontrast zur ersten Schicht also klein,
so reagiert die Phase nicht mehr signifikant auf Änderungen des Widerstands.
Ist die obere Schicht gut leitend (Abbildung 32), so treten deutlich stärkere induktive
Kopplungseffekte auf. Der oberen und unteren Schicht wurde ein Widerstand von 100 Ωm
zugeordnet. Der Widerstand der mittleren Schicht variiert schrittweise von 10 Ωm bis
1000 Ωm.
Wieder zeigt sich, dass hauptsächlich die Leitfähigkeitskontraste die Sensitivität der
Phase beeinflussen. Hier ändert sich die Phase beim Sprung von 10 Ωm auf 100 Ωm (geringer
Kontrast zur oberen Schicht) nur um etwa das Doppelte, beim Übergang von 500 Ωm zu
1000 Ωm (starker Kontrast) ist im Gegensatz zum vorherigen Beispiel aber immer noch ein
deutlicher Unterschied zu erkennen: Es kommt zu einer Abnahme der Phase von etwa 20 %.
Die Leitfähigkeit der oberen Schicht beeinflusst also den Absolutwert der Phase, der
Leitfähigkeitskontrast zur darunter liegenden deren Sensitivität auf Widerstandsänderungen.
30
Schichtmächtigkeiten: 2 m
Widerstände der ersten und
dritten Schicht: 1000 Ωm
25
20
ρ2 = 10 Ωm
ρ2 = 100 Ωm
ρ2 = 500 Ωm
ρ2 = 1000 Ωm
15
10
5
0.1
1
10
Frequenz [Hz]
100
negative Phase [mrad]
35
0
1000
Abbildung 31: Dreischichtfall: Sensitivität bzgl. des Widerstands der mittleren Schicht bei schlecht
leitender Deckschicht und Basis.
Sensitivitätsstudien
45
Schichtmächtigkeiten: 2 m
Widerstände der ersten und
dritten Schicht: 100 Ωm
50
40
ρ2 = 10 Ωm
ρ2 = 100 Ωm
ρ2 = 500 Ωm
ρ2 = 1000 Ωm
0.1
30
20
10
1
10
100
negative Phase [mrad]
60
0
1000
Frequenz [Hz]
Abbildung 32: Dreischichtfall: Sensitivität bzgl. des Widerstands der mittleren Schicht bei gut leitender
Deckschicht und Basis.
In Abbildung 33, Abbildung 34 und Abbildung 35 wird die Sensitivität der Phase
bezüglich der Schichtmächtigkeiten dargestellt. Die drei Beispiele unterscheiden sich dabei
nur in den spezifischen Widerständen der oberen und unteren Schicht (100 Ωm, 500 Ωm und
1000 Ωm). Die mittlere Schicht hat jeweils einen spezifischen Widerstand von 10 Ωm.
Zunächst fällt auf, dass die induktiven Kopplungseffekte auf die Phase im gut leitenden
Untergrund größer sind als im weniger gut leitenden. Ändern sich die spezifischen
Widerstände der oberen und unteren Schicht von 100 Ωm auf 500 Ωm, so ist die Abnahme
der Phase um etwa 30 % deutlich größer als bei einer weiteren Erhöhung der spezifischen
Widerstände von 500 Ωm auf 1000 Ωm (etwa 6 %).
Betrachtet man den Einfluss der Mächtigkeit der mittleren, gut leitenden Schicht auf
die
induktive
Kopplung,
so
erkennt
man
eine
Zunahme
mit
wachsenden
Leitfähigkeitskontrasten. Während in Abbildung 33 die Phase um etwa 36 % kleiner wird,
wenn die Schichtmächtigkeit von 3 m auf 1 m abnimmt, so verringert sie sich in Abbildung
34 um etwa 55 % und in Abbildung 35 sogar um etwa 59 %.
Sensitivitätsstudien
46
ρ1 = 100 Ωm
ρ2 = 10 Ωm
ρ3 = 100 Ωm
d1 und d3 = 2 m
70
d2 = 1.0 m
d2 = 1.5 m
d2 = 2.0 m
d2 = 2.5 m
d2 = 3.0 m
40
0.1
1
60
50
30
20
10
10
100
negative Phase [mrad]
80
0
1000
Frequenz [Hz]
Abbildung 33: Dreischichtfall: Sensitivität bzgl. der Mächtigkeit der zweiten Schicht für eine gut leitende
Deckschicht und Basis.
0.1
ρ1 = 500 Ωm
ρ2 = 10 Ωm
ρ3 = 500 Ωm
d1 und d3 = 2 m
70
d2 = 1.0 m
d2 = 1.5 m
d2 = 2.0 m
d2 = 2.5 m
d2 = 3.0 m
40
1
60
50
30
20
10
10
Frequenz [Hz]
100
negative Phase [mrad]
80
0
1000
Abbildung 34: Dreischichtfall: Sensitivität bzgl. der Mächtigkeit der zweiten Schicht für eine schlecht
leitende Deckschicht und Basis.
Sensitivitätsstudien
47
ρ1 = 1000 Ωm
ρ2 = 10 Ωm
ρ3 = 1000 Ωm
d1 und d3 = 2 m
70
60
50
d2 = 1.0 m
d2 = 1.5 m
d2 = 2.0 m
d2 = 2.5 m
d2 = 3.0 m
0.1
1
40
30
20
10
10
Frequenz [Hz]
100
negative Phase [mrad]
80
0
1000
Abbildung 35: Dreischichtfall: Sensitivität bzgl. der Mächtigkeit der zweiten Schicht für eine sehr schlecht
leitende Deckschicht und Basis.
Änderungen der Schichtmächtigkeit haben einen umso größeren Einfluss auf die
Phase, je größer der Leitfähigkeitskontrast zwischen den einzelnen Schichten ist. Ebenso
reagiert die Kopplung sensitiv beim Übergang von einem insgesamt gut leitenden Untergrund
(Abbildung 33) zu einem insgesamt schlecht leitenden Untergrund (Abbildung 34), während
es danach bei weiterer Verschlechterung der Leitfähigkeit nahezu stabil ist.
3.5 Einfluss von Kabelanordnung und -länge
Bisher wurde die Sensitivität der Phase bezüglich der Untergrundeigenschaften wie
Schichtdicke und Widerstand, sowie der Auslagenkonfiguration wie Elektroden- und
Dipolabstand untersucht. Dabei wurden die Kabel selbst vernachlässigt. Im Folgenden soll
untersucht werden, wie sich Maßnahmen auf die Phase auswirken, die direkt die Kabel
betreffen.
Die Kabel sind Bestandteil der SIP-256C Anlage und haben eine feste Länge, die nicht
variiert werden kann. Dennoch wurde untersucht, ob die Kabellänge einen signifikanten
Einfluss auf die induktive Kopplung hat.
Sensitivitätsstudien
48
Die feste Kabellänge hat außerdem zur Folge, dass die Kabel in der Regel nicht linear
zwischen den Elektroden verlaufen, sondern abhängig vom Elektrodenabstand eine gewisse
orthogonale Anordnung zur Auslagenrichtung aufweisen. Aus diesem Grund wurde
untersucht, ob die Form der Kabelanordnung einen Einfluss auf die Kopplung hat.
Abbildung 36 zeigt den Einfluss der Kabellänge auf die Phase für einen
zweischichtigen Untergrund mit einer Mächtigkeit der ersten Schicht von 2 m und einem
spezifischen Widerstand von 10 Ωm. Der darunter liegende Halbraum hat einen spezifischen
Widerstand von 100 Ωm. Man erkennt, dass selbst bei hohen Frequenzen, die Kurven nahezu
identisch verlaufen, selbst wenn die Kabellänge sich von 5 m auf 20 m vervierfacht. Erst bei
extremen Längenänderungen (100 m, hellblaue Kurve) macht sich der Einfluss bemerkbar,
allerdings auch dann sehr schwach. Derart lange Kabel sind in der Praxis nur dann sinnvoll,
wenn auch die Auslage selbst sehr groß ist. Dann aber haben die großen Elektroden- und
Dipolabstände einen so starken Effekt auf die induktive Kopplung, dass der Einfluss der
Kabellänge vernachlässigt werden kann.
Das in Abbildung 37 dargestellte Beispiel hat im Wesentlichen die gleiche Aussage.
Dabei ist die obere, 2 m dicke Schicht mit einem spezifischen Widerstand von 500 Ωm
schlecht leitend, während der darunter liegende Halbraum mit einem spezifischen Widerstand
von 10 Ωm gut leitend ist. Selbst bei so kontrastierenden Schichten ist der Einfluss der
Kabellänge marginal. Erst bei sehr großen Kabellängen tritt überhaupt ein Effekt auf, der aber
wiederum so gering ist, dass er von den Effekten, die Elektroden- und Dipolabstand haben,
überlagert würde.
Allgemein ist die Länge der verwendeten Kabel also nicht wichtig für die
Kopplungseffekte.
Sensitivitätsstudien
49
d1 = 2 m
ρ1 = 10 Ωm
ρ2 = 100 Ωm
50
40
Kabellänge: 5 m
Kabellänge: 10 m
Kabellänge: 20 m
Kabellänge: 100 m
30
20
10
0.1
1
10
100
negative Phase [mrad]
60
0
1000
Frequenz [Hz]
Abbildung 36: Einfluss der Kabellänge auf die induktive Kopplung bei gut leitender Deckschicht und
schlechter leitender Basis in einem Zweischichtfall.
160
d1 = 2 m
ρ1 = 500 Ωm
ρ2 = 10 Ωm
140
120
Kabellänge: 5 m
Kabellänge: 10 m
Kabellänge: 20 m
Kabellänge: 100 m
100
80
60
40
20
0.1
1
10
100
negative Phase [mrad]
180
0
1000
Frequenz [Hz]
Abbildung 37: Einfluss der Kabellänge auf die induktive Kopplung bei schlecht leitender Deckschicht und
gut leitender Basis in einem Zweischichtfall.
Sensitivitätsstudien
50
Es stellt sich nun die Frage, inwieweit die Kabelanordnung eine Rolle bei der
induktiven Kopplung spielt. Die Untersuchungen dazu wurden hinsichtlich der realen
Kabellänge der SIP256C Anlage bei einer konstanten Kabellänge von 10 m durchgeführt.
Es wurden die in Abbildung 38 dargestellten vier Anordnungen untersucht und
gegenübergestellt. Dabei wurden die gleichen Untergrundmodelle verwendet wie bei der
Untersuchung des Einflusses der Kabellänge. Die in Abbildung 39 und Abbildung 40
dargestellten Ergebnisse zeigen keinen Effekt der Kabelanordnung auf die induktive
Kopplung.
Es spielt also keine Rolle, wie die Kabel zwischen den Elektroden angeordnet
werden.
Geometrie 1
5m
5m
Geometrie 2
4m
4m
2m
2m
Geometrie 3
Geometrie 4
2m
2m
1m
2m
2m
Abbildung 38: Die vier Geometrien der untersuchten Kabelanordnungen. Die Kreise bezeichnen jeweils
die Elektroden.
Sensitivitätsstudien
51
d1 = 2 m
ρ1 = 10 Ωm
ρ2 = 100 Ωm
50
40
Geometrie 1
30
Geometrie 2
Geometrie 3
20
Geometrie 4
10
0.1
1
10
100
negative Phase [mrad]
60
0
1000
Frequenz [Hz]
Abbildung 39: Einfluss der Kabelanordnung auf die induktive Kopplung bei gut leitender Deckschicht
und schlechter leitender Basis in einem Zweischichtfall.
160
d1 = 2 m
ρ1 = 500 Ωm
ρ2 = 10 Ωm
140
120
Geometrie 1
100
Geometrie 2
Geometrie 3
80
60
Geometrie 4
40
20
0.1
1
10
100
negative Phase [mrad]
180
0
1000
Frequenz [Hz]
Abbildung 40: Einfluss der Kabelanordnung auf die induktive Kopplung bei schlecht leitender
Deckschicht und gut leitender Basis in einem Zweischichtfall.
Sensitivitätsstudien
52
3.6 Zusammenfassung der Sensitivitätsstudien
In Sensitivitätsstudien wurde der Einfluss verschiedener Parameter auf die induktive
Kopplung untersucht. Dabei konnte gezeigt werden, dass Kabelanordnung und -länge keinen
signifikanten Einfluss haben. Bei Mehrschichtfällen üben Elektrodenabstand und Dipollänge
der verwendeten Auslage den größten Einfluss aus. Beide Parameter sind in der Praxis jedoch
sehr genau einstellbar. Anders verhält es sich bei den Untergrundeigenschaften, die aus
Tiefensektionen abgelesen werden müssen. Es wurde gezeigt, in welcher Weise
Schichtmächtigkeit und spezifischer Widerstand der Schichten die induktive Kopplung
beeinflussen. Besonders bei großen Kontrasten sind die verursachten Effekte sehr stark. Je
homogener sich der Untergrund gestaltet, desto geringer wirkt sich die induktive Kopplung
aus.
Ferner wurden Untersuchungen für den homogenen Halbraum angestellt. Dabei wurde
speziell der lineare Zusammenhang der durch induktive Kopplung verursachten
Phasenverschiebung und der Frequenz untersucht. Daraus konnte eine einfache Formel zur
Abschätzung der induktiven Kopplung über homogenem Halbraum abgeleitet werden. In
Parameterstudien wurde zudem untersucht, in welchen Fällen ein Mehrschichtfall genähert als
homogener Halbraum betrachtet werden kann.
Feldmessungen
53
4 Feldmessungen
4.1 Motivation
In diesem Kapitel werden die Ergebnisse von Feldmessungen vorgestellt. Deren Ziel
war zum einen die Überprüfung der mit dem Programm IP3C durchgeführten
Sensitivitätsstudien, zum anderen die Korrektur der gemessenen Daten. Aus den korrigierten
Daten sollen dann Tiefensektionen erstellt werden, die von induktiven Kopplungseffekten
weitestgehend befreit sind.
Die im Rahmen dieser Arbeit durchgeführten Messkampagnen fanden in drei
verschiedenen Gebieten statt: Dem Braunkohletagebau Inden und dem Testgelände
Krauthausen, die sich beide in der Nähe von Jülich befinden und einem Testgelände bei Kall
in der nördlichen Eifel.
Neben den durchgeführten SIP-Messungen wurde eine Reihe von Experimenten
durchgeführt, um den Einfluss verschiedener Parameter auf die induktive Kabelkopplung zu
untersuchen.
Bei allen durchgeführten Messungen wurden Dipol-Dipol-Auslagen verwendet. In
Abbildung 41 ist die Geometrie der Anlage SIP256C skizziert.
Mobilstationen
Basisstation
1
2
3
4
5
6
7…
…20
Elektroden
Abbildung 41: Skizze der verwendeten Auslage. Die Quadrate stellen die Basis- bzw. Mobilstationen dar,
die Kreise die Elektroden.
4.2 Einfluss der Kabelanordnung
Die Sensitivitätsstudien mit dem Programm IP3C haben gezeigt, dass die Form des
Verlaufs der Kabel zwischen den Elektroden keinen Einfluss auf die induktive Kopplung hat.
Feldmessungen
54
Die experimentelle Überprüfung dieses Ergebnisses wurde in zwei Feldmessungen erbracht.
Dazu wurde im Braunkohletagebau Inden untersucht, ob die Anordnung der auf dem Boden
liegenden Kabel einen Einfluss auf die Messungen hat. Im Messgebiet Kall wurde zudem
untersucht, ob es einen Einfluss hat, wenn die Kabel während der Messung keinen Kontakt
zum Boden haben.
Bei der Messung in Inden am 17. April 2007 wurde ein Elektrodenabstand von
a = 2 m gewählt, so dass die Gesamtauslage eine Länge von 40 m hatte. Es wurde über ein
Frequenzspektrum von 125 mHz bis 1 kHz gemessen. Wie erwartet treten ab etwa 40 Hz
deutliche Kopplungseffekte in den Daten auf (Abbildung 42).
16
14
Stromelektroden: 1 und 2
12
Stromelektroden: 3 und 4
10
Stromelektroden: 5 und 6
8
6
4
2
0.1
1
10
100
negative Phase [mrad]
18
Potentialelektroden: 14 und 15
Kabel beliebig
0
1000
Frequenz [Hz]
Abbildung 42: Drei Phasenspektren der Messung in Inden im Vergleich.
Es wurden zwei Messreihen durchgeführt. In der ersten wurden die Kabel zwischen
den Elektroden weitestgehend aufgerollt gelassen (Geometrie 4 in Abbildung 38), während
sie für die zweite Messreihe senkrecht von der Auslagenrichtung weg in einer Dreiecksform
ausgelegt wurden (Geometrie 1 in Abbildung 38). Die Ergebnisse sind in Abbildung 43
dargestellt. Man erkennt keinen signifikanten Unterschied im Kurvenverlauf, weder für kleine
Frequenzen, bei denen keine induktive Kopplung auftritt, noch bei größeren Frequenzen, wo
deutliche Kopplungseffekte die Spektren überlagern.
Feldmessungen
55
aufgerollte Kabel
14
dreieckige Kabelanordnung
aufgerollte Kabel
12
n = 12
10
dreieckige Kabelanordnung
8
6
n=2
4
2
0.1
1
10
100
negative Phase [mrad]
16
0
1000
Frequenz [Hz]
Abbildung 43: Inden: Phasenspektren zur Untersuchung des Einflusses der Kabelanordnung.
Abbildung 44 zeigt das gleiche Ergebnis für andere Dipolabstände n⋅a.
aufgerollte Kabel
14
dreieckige Kabelanordnung
aufgerollte Kabel
dreieckige Kabelanordnung
12
n = 10
10
8
6
n=4
4
2
0.1
1
10
100
0
1000
Frequenz [Hz]
Abbildung 44: Inden: Phasenspektren zur Untersuchung des Einflusses des Kabelanordnung.
negative Phase [mrad]
16
Feldmessungen
56
Die horizontale Ausrichtung der Kabel hat bei Dipol-Dipol-Auslagen offenbar keinen
signifikanten Effekt auf die induktive Kopplung. Das bestätigt die Sensitivitätsstudien bzgl.
dieses Parameters. Es muss bei Feldmessungen also nicht darauf geachtet werden, wie die
Kabel angeordnet sind.
Daraufhin wurde untersucht, ob es einen Einfluss auf die induktive Kopplung hat,
wenn die Kabel keinen direkten Kontakt zum Boden haben. Außerdem diente dies dem
Zweck zu untersuchen, ob die kapazitive Kopplung einen Einfluss hat. Dazu wurden zwei
Messungen im Testgebiet Kall am 15. Mai 2007 durchgeführt. Es wurde ein
Elektrodenabstand von a = 0,5 m gewählt und bei 12 verschiedenen Frequenzen zwischen
250 mHz und 1 kHz gemessen. Die Gesamtauslage war 10 m. Bei der ersten Messreihe lagen
die Kabel weitestgehend aufgerollt auf dem Boden. Bei der zweiten Messreihe wurden sie an
1,80 m hohen Plastikspießen aufgehängt, sodass sie keinen direkten Kontakt zum Boden
hatten (Abbildung 45). Dieser Fall kann mit dem Programm IP3C nicht simuliert werden und
wurde deshalb lediglich in der Feldmessung untersucht.
Abbildung 46 zeigt die bei den unterschiedlichen Kabelanordnungen aufgenommenen
Frequenzspektren. Es sind auch in diesem Fall keine wesentlichen Unterschiede zwischen den
beiden Messreihen erkennbar, weder bei niedrigen Frequenzen, noch im höheren
Frequenzbereich.
Abbildung 45: Kabelgeometrie in Kall.
Feldmessungen
Kabel aufgerollt
Kabel aufgehängt
Kabel aufgerollt
Kabel aufgehängt
n = 17
n=4
0.1
1
10
100
30
25
20
15
10
5
0
-5
-10
-15
-20
1000
negative Phase [mrad]
57
Frequenz [Hz]
Abbildung 46: Kall: Vergleich der Spektren bei auf dem Boden liegenden und aufgehängten Kabeln.
In Abbildung 47 sind Spektren anderer Dipolabstände dargestellt. Die Kurven
Kabel aufgerollt
Kabel aufgehängt
Kabel aufgerollt
Kabel aufgehängt
0.1
1
10
100
30
n = 2 20
10
0
-10
-20
-30
-40
-50
n = 10
-60
-70
-80
1000
negative Phase [mrad]
verlaufen jeweils wiederum nahezu identisch.
Frequenz [Hz]
Abbildung 47: Kall: Vergleich der Spektren bei auf dem Boden liegenden und aufgehängten Kabeln.
Feldmessungen
58
Die induktive Kopplung kann also durch das Aufhängen der Kabel nicht reduziert
werden. Es kann bei Feldmessungen also auf aufwändige Kabelanordnungen verzichtet
werden. Auch die kapazitive Kopplung beeinflusst die Messwerte hier nicht.
Im Zusammenhang mit dieser Messreihe ist auch die Betrachtung der kapazitiven
Kopplung interessant. Der Unterschied zwischen den beiden Messanordnungen ist eine
1,80 m dicke Luftschicht, die sehr schlecht leitend ist und einen großen Übergangswiderstand
darstellt. Somit sollte im Vergleich zu den auf dem Boden liegenden Kabeln deutlich weniger
Strom in den Untergrund abfließen. Dennoch sind die Spektren für beide Anordnungen
nahezu identisch. Offenbar ist somit der Einfluss der kapazitiven Kopplung für SIPMessungen in diesem Frequenzbereich vernachlässigbar.
4.3 Einfluss der Kabellänge
Die Simulationen mit dem Programm IP3C haben gezeigt, dass die Kabellänge keine
signifikanten Effekte auf die Phase hat. Eine Überprüfung dieses Ergebnisses in der Praxis
wurde bei einer Messung auf dem Testgelände Krauthausen am 16. November 2007
angestrebt. Bei der Messapparatur SIP256C sind die Kabel fest installiert und haben zwischen
den Mobilstationen eine Länge von jeweils 10 m. Zur Untersuchung der Effekte einer
Änderung der Kabellänge wurden deshalb Verlängerungskabel verwendet, mit denen die
Länge auf 20 m vergrößert werden konnte. Bei der Messung betrug der Abstand zwischen den
Elektroden 2 m. Gemessen wurde bei 10 Frequenzen zwischen 1,25 Hz und 1 kHz.
In Abbildung 48 sind Phasenspektren dreier verschiedener Dipolabstände dargestellt.
Sie wurden einmal bei der gerätespezifischen Kabellänge von 10 m aufgenommen
(durchgezogene Kurven), einmal bei der doppelten Kabellänge von 20 m (gestrichelte
Kurven). Man erkennt für keinen der drei Dipolabstände erhebliche Abweichungen aufgrund
der unterschiedlichen Kabellänge. Damit kann ein Einfluss auch dieser Größe auf die
induktive Kopplung ausgeschlossen werden.
Feldmessungen
59
8
n=2
6
n=5
4
Stromelektroden: 1 und 2
Durchgezogene Kurven: 10 m Kabel
Gestrichelte Kurven: 20 m Kabel
2
0
-2
1
10
100
negative Phase [mrad]
10
n=1
-4
1000
Frequenz [Hz]
Abbildung 48: Krauthausen: Phasenspektren zur Untersuchung des Einflusses der Kabellänge.
4.4 Einfluss des Dipolabstands
Aufgrund der Spezifikationen der SIP256C Anlage wird bei jeder Messung über
verschiedene Dipolabstände gemessen. Aus den Sensitivitätsstudien geht hervor, dass dieser
Parameter einen starken Einfluss auf die induktive Kopplung hat. Zur Bestätigung dieser
theoretischen Ergebnisse sollen in diesem Kapitel die Feldmessungen in Inden am 17. April
2007 und in Krauthausen am 23. August 2007 betrachtet werden.
In Inden betrug der Elektrodenabstand 2 m, in Krauthausen 1,5 m. Damit variierte der
Dipolabstand in der ersten Messung zwischen 2 m und 36 m, in der zweiten zwischen 1,5 m
und 15 m.
In Abbildung 49 sind die in Inden aufgenommenen Phasenspektren für drei
verschiedene Dipolabstände gezeigt. Der Strom wurde über die siebte und achte Elektrode in
den Boden eingespeist. Die dargestellten Spektren sind bei Dipolabständen von 4 m, 12 m
und 20 m aufgenommen worden. Man erkennt, wie mit wachsendem Dipolabstand die
negative Phase zunimmt. Im niederfrequenten Bereich verlaufen die Kurven der
Dipolabstände 12 m und 20 m (rote und grüne Kurven) nahezu identisch. Die Kurve des
Dipolabstands 4 m (blaue Kurve) liegt bei 0,25 Hz etwa 3 mrad unter den beiden anderen und
verläuft erst ab etwa 5 Hz auf gleichem Niveau. Die induktive Kopplung setzt bei etwa 40 Hz
Feldmessungen
60
ein und führt zu einem stärkeren Ansteigen der negativen Phase, je größer der Dipolabstand
ist. Das Auseinanderlaufen der blauen Kurve im niederfrequenten Bereich kann nicht auf
Kopplung zurückgeführt werden. Offenbar hat der spezifische Widerstand des Gesteins in der
diesem Dipolabstand entsprechenden Tiefe von etwa 1 m eine andere Phase als das tiefer
liegende.
Die gestrichelten Spektren sind die Simulationen der induktiven Kopplung für die
entsprechenden Dipolabstände. Dabei wurde ausschließlich der durch induktive Kopplung
hervorgerufene Anteil der Phase simuliert, nicht der durch den IP-Effekt hervorgerufene. Das
führt zu der Abweichung der simulierten von den gemessenen Phasen. Damit wird
gewährleistet, dass mit dem Abzug der simulierten Phase von den Messwerten nicht auch der
Anteil des IP-Effektes verschwindet.
Der Einfluss des Dipolabstands auf die induktive Kopplung in den Simulationen
entspricht in guter Näherung dem Verlauf der gemessenen Spektren bei hohen Frequenzen.
Stromelektroden: 7 und 8
25
n=2
n=6
n = 10
n = 2 simuliert
n = 6 simuliert
n = 10 simuliert
20
15
10
5
0.1
1
10
100
negative Phase [mrad]
30
0
1000
Frequenz [Hz]
Abbildung 49: Inden: gemessene und simulierte Spektren bei verschiedenen Dipolabständen.
Die Ergebnisse der Messung in Krauthausen (Abbildung 50) zeigen ebenfalls die
Abhängigkeit der induktiven Kopplung vom Dipolabstand, der hier 3 m, 9 m und 15 m
betrug. Im niederfrequenten Bereich sieht man weitgehend konstante Phasen. Die induktive
Kopplung setzt ab etwa 60 Hz ein und überlagert die Spektren. Das bei einem Dipolabstand
von 9 m aufgenommene Spektrum liegt im niederfrequenten Bereich stets unterhalb der
Feldmessungen
61
anderen beiden Spektren. Es scheint hier eine Schicht geringerer Phase aufzuweisen, die
zwischen zwei Schichten mit größeren Phasen eingebettet ist.
Oberhalb von etwa 450 Hz weisen die Kurven der beiden größeren Dipolabstände
(rote und grüne Kurven) zunächst eine starke Zunahme der Phase auf, die dann bei höheren
Frequenzen wieder etwas zurückgeht. Im Spektrum des geringsten Dipolabstands ist dieser
Knick weniger stark ausgebildet, aber dennoch zu erkennen.
Die gestrichelten Kurven weisen wieder auf die Simulationen der entsprechenden
Phasenspektren hin. Der Verlauf der gemessenen Spektren wird gut reproduziert, mit
Ausnahme des Knicks im Phasenverlauf zwischen 450 Hz und 1 kHz.
Stromelektroden: 7 und 8
n=2
n=6
n = 10
n = 2 simuliert
n = 6 simuliert
n = 10 simuliert
25
20
15
10
5
0.1
1
10
100
negative Phase [mrad]
30
0
1000
Frequenz [Hz]
Abbildung 50: Krauthausen: gemessene und simulierte Spektren bei verschiedenen Dipolabständen.
4.5 Tiefensektionen
Ziel von SIP-Messungen ist die Sondierung des Untergrunds, um Aussagen über
Gesteinseigenschaften und Untergrundbeschaffenheit zu treffen. Aus diesem Grund werden
die gemessenen Daten invertiert und die Ergebnisse für jede Frequenz in Tiefensektionen
dargestellt. Darin werden die Bereiche homogener Widerstands- und Phasenverteilung im
Untergrund einer bestimmten Tiefe und einem bestimmten Bereich entlang des Profils
zuordnet.
Feldmessungen
62
In diesem Kapitel werden die im Rahmen dieser Arbeit erhobenen Felddaten invertiert
und in Tiefensektionen dargestellt. Im nächsten Schritt wird der Versuch unternommen die
induktiven Kopplungseffekte aus den Felddaten herauszurechnen, diese korrigierten Daten zu
invertieren und korrigierte Tiefensektionen zu erstellen. Dazu müssen von allen Felddaten die
simulierten induktiven Kopplungseffekte abgezogen werden. Das geschieht aufgrund der zum
Teil sehr großen Datensätze mittels eines Matlab-Programms, das zu diesem Zweck
geschrieben wurde. Als Ausgabe erhält man einen korrigierten Datensatz, der invertiert
werden kann. Für die Inversion wird das Programm RES2DINV [Geotomo Software, 2004]
genutzt, das für jede Frequenz eine Tiefensektion ausgibt. Diese korrigierten Tiefensektionen
werden mit den unkorrigierten verglichen, wobei besonders die durch Kopplung beeinflussten
Sektionen bei hohen Frequenzen von Interesse sind. Die korrigierten und unkorrigierten
Tiefensektionen bei niedrigeren Frequenzen sollten sich nicht unterscheiden, da in den Daten
keine signifikanten induktiven Kopplungseffekte auftreten.
In Abbildung 51 sind solche Tiefensektionen bei niedrigen Frequenzen für das
Messgebiet Inden dargestellt, anhand derer die Untergrundstruktur zur Simulation mit dem
Programm
IP3C
abgelesen
werden
kann.
Man
erkennt
drei
verschiedene
Widerstandsbereiche. Es gibt eine obere gut leitende Schicht von etwa 2,5 m Dicke, deren
Widerstand für die Simulation mit 20 Ωm angenommen wurde. Darunter schließt sich eine
etwa 4 m mächtige Schicht höherer Widerstände an. Für die Simulation wurde für diesen
Bereich ein homogener Widerstand von 200 Ωm angenommen. Unterhalb dieser Schicht
befindet sich ein Bereich höherer Leitfähigkeiten. Der Widerstand wurde mit 50 Ωm
gemittelt. Mit diesen Informationen wurde unter Berücksichtigung der Messgeometrie die
Simulation mit dem Programm IP3C durchgeführt.
In der Tiefensektion der Phase erkennt man eine weitgehend homogene Verteilung mit
einer Tendenz zu wachsenden negativen Phasenwerten bei größer werdenden Tiefen, wie
auch schon aus den in Abbildung 49 dargestellten Phasenspektren gedeutet wurde.
Feldmessungen
Tiefe [m]
0
63
5
Profil [m]
15
20
10
25
30
35
-5
50 100 150 200 250 300
Widerstand [Ω m]
Tiefe [m]
0
5
Profil [m]
15
20
10
25
30
35
-5
0
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 51: Inden: unkorrigierte Tiefensektionen für Widerstand (oben) und Phase (unten) bei 1 Hz.
Abbildung 52 zeigt die Korrektur der in Abbildung 49 dargestellten Phasenspektren.
Im niederfrequenten Bereich ist die Korrektur unerheblich, erst ab etwa 40 Hz dämpft sie den
Anstieg der negativen Phase. Man erkennt immer noch die generell wachsende Tendenz,
jedoch liegt sie jetzt im Rahmen der Steigung, die die Kurven im niederfrequenten Bereich
aufweisen.
Feldmessungen
64
25
n=2
n=6
n = 10
20
15
10
5
0.1
1
10
100
negative Phase [mrad]
30
Stromelektroden: 7 und 8
0
1000
Frequenz [Hz]
Abbildung 52: Inden: korrigierte Phasenspektren (vgl. Abbildung 49).
Die in Krauthausen aufgenommenen Daten wurden zur in Abbildung 53 dargestellten
Tiefensektion invertiert. Es liegt offenbar ein Dreischichtfall mit einer schlecht leitenden
mittleren Schicht vor, die von zwei besser leitenden eingeschlossen wird. Der Widerstand der
etwa 1 m dicken oberen Schicht wurde mit 25 Ωm abgelesen, der der unteren mit 90 Ωm. Die
schlecht leitende mittlere Schicht hat eine Dicke von etwa 3,5 m und einen mittleren
Widerstand von etwa 200 Ωm. Unter Berücksichtigung der Messgeometrie in Krauthausen
wurde die Kopplung mit diesen Untergrundinformationen simuliert.
Feldmessungen
Tiefe [m]
0
65
5
10
Profil [m]
15
20
25
-2
-4
-6
50
100 150 200 250 300
Widerstand [Ω m]
Tiefe [m]
0
5
10
Profil [m]
15
20
25
-2
-4
-6
0
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 53: Krauthausen: unkorrigierte Tiefensektionen für Widerstand (oben) und Phase (unten) bei
1 Hz.
In Abbildung 54 sind die Spektren aus Abbildung 50 korrigiert dargestellt. Die
Korrektur ist ab etwa 80 Hz signifikant. Die negative Phase steigt hin zu hohen Frequenzen
nicht mehr so stark an. Der Knick bei etwa 450 Hz ist immer noch in allen drei Kurven
erkennbar. Er geht offenbar auf schlechte Datenqualität bei dieser Frequenz zurück.
Feldmessungen
66
25
n=2
n=6
n = 10
20
15
10
5
0.1
1
10
100
negative Phase [mrad]
30
Stromelektroden: 7 und 8
0
1000
Frequenz [Hz]
Abbildung 54: Krauthausen: korrigierte Phasenspektren (vgl. Abbildung 50).
Hinsichtlich der Fülle von Daten wurde sich hier auf die Präsentation zweier Beispiele
beschränkt. Tatsächlich wurden die Simulationen zur Korrektur aller aufgenommenen
Spektren verwendet. Diese korrigierten Daten wurden dann invertiert und führten zu der in
Abbildung 55 dargestellten korrigierten Tiefensektion bei 1 kHz in Inden. Zum Vergleich ist
in Abbildung 56 die unkorrigierte Tiefensektion bei 1 kHz dargestellt. Darin sind viele
Bereiche erhöhter Phasen zu sehen, die besonders im hinteren Teil der Auslage zum Teil sehr
stark zunehmen. Betrachtet man die korrigierte Tiefensektion, so zeigt sich ein sehr viel
homogenerer Untergrund. Die Phasenwerte sind deutlich geringer und liegen weitgehend
unterhalb von -6 mrad. Zu einer Phasenerhöhung kommt es ab einer Auslagenweite von etwa
24 m in einer Tiefe von etwa 2,5 m. Der Vergleich mit der Tiefensektion bei 1 Hz (Abbildung
51) zeigt, dass der Anstieg in dieser Region auch im niederfrequenten Bereich zu erkennen
ist, wenn auch weniger stark ausgeprägt.
Einen weiteren Bereich hoher Phasenwerte erkennt man am Anfang der Auslage
zwischen 2,5 m und 5 m. Dort sieht man in der Tiefensektion der kleineren Frequenz keine
erhöhten Werte.
Allgemein ist bei der Deutung der Tiefensektionen darauf zu achten, dass die
Datendichte im Bereich der Ränder der Auslage gering ist. Oft reichen in dem Bereich wenige
fehlerhafte Datenpunkte um in der Invertierung als Anomalien dargestellt zu werden. Es ist
daher ratsam die korrigierten Tiefensektionen nur im Zusammenhang mit den dazugehörigen
Feldmessungen
67
unkorrigierten Tiefensektionen, als auch mit Tiefensektionen im niederfrequenten Bereich zu
betrachten.
Die Widerstandstiefensektionen zeigen keine signifikanten Fehler aufgrund induktiver
Kopplung. Sie sind über das gesamte verwendete Frequenzband hinweg nahezu konstant.
Tiefe [m]
0
5
Profil [m]
15
20
10
25
30
35
-5
50
100 150 200 250 300
Widerstand [Ω m]
Tiefe [m]
0
5
Profil [m]
15
20
10
25
30
35
-5
0
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 55: Inden: korrigierte Tiefensektionen für Widerstand (oben) und Phase (unten) bei 1 kHz.
Feldmessungen
Tiefe [m]
0
68
5
Profil [m]
15
20
10
25
30
35
-5
0
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 56: Inden: unkorrigierte Tiefensektion der Phase bei 1 kHz.
Für die in Krauthausen gemessenen Daten wurde ebenso verfahren. Die korrigierte
Tiefensektion für 1 kHz ist in Abbildung 57 dargestellt. Abbildung 58 zeigt im Vergleich
dazu die unkorrigierte Tiefensektion, in der eine Vielzahl von Bereichen stark erhöhter
Phasenwerte zu erkennen ist. In der korrigierten Tiefensektion stellt sich der Untergrund
weniger heterogen dar. Es gibt Bereiche leichter Phasenerhöhungen bei 6 m und 11 m entlang
des Profils, sowie einen Bereich großer Phasenwerte zwischen 16 m und 20 m, der sich in
einer Tiefe zwischen 1 m und 5 m befindet. Zusätzlich zeigt sich auch hier ein kleiner Bereich
hoher Phase am Anfang des Profils. Dabei handelt es sich um den Bereich geringer
Datendichte, was nahe legt, diese Anomalie zu ignorieren. Interessant bei der Betrachtung der
Tiefensektion ist die große Anomalie, die zwischen 16 m und 20 m entlang des Profils
angezeigt wird. Dort erreicht die Phase Werte bis zu -30 mrad, während sie in der Umgebung
unter -6 mrad liegen. In dem gleichen Bereich in der Tiefensektion des spezifischen
Widerstands erkennt man eine schlecht leitende Struktur mit Werten bis etwa 300 Ωm. Der
Vergleich der beiden Tiefensektionen lässt also darauf schließen, dass sich an dieser Stelle ein
Artefakt befindet.
Feldmessungen
Tiefe [m]
0
69
5
10
Profil [m]
15
20
25
-2
-4
-6
50
100 150 200 250 300
Widerstand [Ω m]
Tiefe [m]
0
5
10
Profil [m]
15
20
25
-2
-4
-6
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 57: Krauthausen: korrigierte Tiefensektionen für Widerstand (oben) und Phase (unten) bei 1
kHz.
Feldmessungen
Tiefe [m]
0
70
5
Profil [m]
15
10
20
25
-2
-4
-6
0
5
10
15
20
25
30
negative Phase [mrad]
Abbildung 58: Krauthausen: unkorrigierte Tiefensektion der Phase bei 1 kHz.
In Abbildung 59 sind drei Phasenspektren dargestellt, die in verschiedenen Tiefen bei
gleicher lateraler Profilkoordinate aufgenommen wurden (Abbildung 60). Dabei handelt es
sich um die invertierten Daten, die aus den Tiefensektionen der Phase bei allen verwendeten
Frequenzen gewonnen wurden. Diese Spektren geben Aufschluss über das spektrale
Verhalten des Gesteins an den jeweiligen Punkten im Untergrund und können einer weiteren
geologischen Interpretation dienen.
12
10
8
6
4
2
0.1
1
10
100
negative Phase [mrad]
14
z = -0,128 m x = 14,3 m
z = -2,55 m
z = -4,06 m
0
1000
Frequenz [Hz]
Abbildung 59: Phasenspektren für drei verschiedene Tiefen z am Punkt x = 14,3 m entlang der Auslage.
Feldmessungen
Tiefe [m]
0
71
5
10
Profil [m]
15
20
25
-2
-4
-6
50
100 150 200 250 300
Widerstand [Ω m]
Abbildung 60: Krauthausen: Tiefensektion des Widerstands. Die Kreise bezeichnen die Punkte, an denen
die Phasenspektren extrahiert wurden.
Man erkennt ähnliche Verläufe der Spektren für die Tiefen z = -2,55 m und
z = -4,06 m. Die negativen Phasen steigen zunächst mit wachsender Frequenz an, um dann
hin zu großen Frequenzen wieder abzufallen. Das Spektrum bei der Tiefe z = -0,128 fällt
zunächst leicht ab und steigt ab etwa 200 Hz wieder an. In dieser geringen Tiefe ist der
Untergrund sehr gut leitend im Vergleich zu darunter liegendem Gestein, wodurch der
Verlauf des Phasenspektrums beeinflusst wird.
4.6 Probleme bei der Korrektur der Daten
In diesem Abschnitt erfolgt eine kritische Betrachtung des Korrekturschemas der
Daten. Es wird die Frage aufgeworfen, in wie weit man den korrigierten Tiefensektionen
vertrauen kann und wie eine größtmögliche Verlässlichkeit erreicht werden kann.
Die Qualität der gemessenen Felddaten variiert zum Teil sehr stark. Es ist daher
angeraten die Datensätze zu betrachten, bevor mit der eigentlichen Korrektur begonnen wird.
Bei 20 Elektroden ist es häufig der Fall, dass die Messungen einzelner Elektroden
systematisch fehlerhafte Daten liefern, sei es aufgrund eines zu großen Übergangswiderstands
zum Boden (also schlechter galvanischer Ankopplung), schwacher Batterieleistung der
Feldmessungen
72
Mobilstation oder anderer äußerer Störeinflüsse. Erkennt man solche wiederkehrenden Fehler
im Datensatz, sollten die Daten der entsprechenden Elektroden nicht für die Inversion
verwendet werden. Ansonsten besteht die Gefahr in den Tiefensektionen Anomalien zu
erzeugen, die nicht von Artefakten herrühren.
Nach dieser ersten Korrektur des Datensatzes werden Tiefensektionen bei niedrigen
Frequenzen erzeugt, um ein Untergrundmodell für die Simulation mit dem Programm IP3C zu
erstellen. Beim Ablesen der Anzahl der Schichten, deren Mächtigkeiten und Widerstände
taucht eine weitere Fehlerquelle auf. Die Schichten werden als horizontal und homogen
betrachtet,
was
jedoch
in
der
Regel
nur
eine
Näherung
der
tatsächlichen
Untergrundbegebenheiten darstellen kann. Die Erstellung des Modells muss unter
Berücksichtigung der Ergebnisse aus den Sensitivitätsstudien erfolgen, um die Fehler in
diesem
Bereich
zu
minimieren.
Insbesondere
sollte
vermieden
werden,
große
Leitfähigkeitskontraste zu erzeugen, indem man zwei benachbarten Schichten jeweils
Extremwerte ihrer Widerstandsverteilung zuordnet.
Bei den im Rahmen dieser Arbeit durchgeführten Messungen stellte sich der
Untergrund in guter Näherung meist als horizontaler Mehrschichtfall mit verhältnismäßig klar
definierten Grenzen dar. Das muss im Allgemeinen nicht zutreffen. Das Programm IP3C
bietet die Möglichkeit Anomalien im Untergrund bei der Simulation der induktiven Kopplung
zu berücksichtigen. Eine variable Topographie kann nicht berücksichtigt werden.
Eine korrigierte Tiefensektion sollte nicht isoliert interpretiert werden, sondern im
Zusammenhang der bei anderen Frequenzen erstellten Tiefensektionen, speziell solcher im
niederfrequenten Bereich und ohne induktiven Kopplungseffekte. Auch ein Vergleich mit den
unkorrigierten Tiefensektionen bei gleichen Frequenzen ist sinnvoll, um eventuelle Überoder Unterkorrekturen zu erkennen. Damit vermeidet man das Interpretieren von Anomalien,
die
wiederum
auf
Kopplungseffekte
Untergrundbeschaffenheit beruhen.
zurückzuführen
sind
und
nicht
auf
der
Zusammenfassung und Ausblick
73
5 Zusammenfassung und Ausblick
Neuere Arbeiten zeigen, dass die Interpretation der Frequenzabhängigkeit des
elektrischen Widerstandes (bzw. seiner Phase) unter anderem zur Ableitung der hydraulischen
Permeabilität genutzt werden kann [Slater, 2007]. Damit diese Analysen auf Feldmessungen
übertragen werden können, muss sichergestellt werden, dass die gemessenen Spektren nicht
durch Kopplungseffekte beeinflusst sind. In der Praxis wird jedoch aufgrund der
Kabelkopplungseffekte nur der niederfrequente Bereich des Spektrums bis etwa 40 Hz
betrachtet, so dass die im spektralen Verhalten der Phase liegenden Informationen verloren
gehen. Aus diesem Grund wurde im Rahmen der vorliegenden Arbeit der Ansatz verfolgt, die
induktiven Kopplungseffekte numerisch zu simulieren, um sie nachträglich aus den
gemessenen SIP-Daten herauszurechnen. Die Einflussfaktoren auf die induktive Kopplung
wurden anhand von Sensitivitätsstudien untersucht. Diese Studien wurden durch
Feldmessungen ergänzt, bei denen die Einflüsse der verschiedenen Größen validiert wurden.
Dabei konnte gezeigt werden, dass weder die Kabelanordnung, noch die Länge der Kabel
einen signifikanten Einfluss auf die induktive Kopplung haben. Anders verhält es sich mit
dem spezifischen Widerstand des Untergrunds, der Schichtdicken, der Elektroden- und
Dipolabstände.
Insbesondere
bei
Mehrschichtfällen
im
Untergrund,
die
starke
Leitfähigkeitskontraste aufweisen sind die Effekte der induktiven Kopplung auf die Phase
sehr groß. Diese Effekte nehmen zu, je größer die Elektroden- und Dipolabstände der Auslage
gewählt werden. In einer Messreihe mit aufgehängten Kabeln konnte ein Einfluss kapazitiver
Kopplung auf die Phase ausgeschlossen werden (für die im Rahmen dieser Arbeit
durchgeführten Messungen über horizontal geschichtetem Untergrund).
Unter
Berücksichtigung
der
Ergebnisse
der
Sensitivitätsstudien
und
den
Feldmessungen wurde die Korrektur der Felddaten durchgeführt. Damit war es möglich,
durch Inversion Tiefensektionen für Frequenzen bis 1 kHz zu erhalten, die weitgehend von
induktiven Kopplungseffekten befreit sind. Die dabei auftretenden Probleme wurden kritisch
diskutiert.
Die Frage, ob die korrigierten Tiefensektionen dem realen Untergrund entsprechen,
kann hier leider nicht abschließend beantwortet werden. Zur Überprüfung der
Kopplungskorrektur könnten eventuell Laborversuche an Proben mit bekannten SIPEigenschaften durchgeführt werden, wobei im Labor aufgrund der geringen Dimensionen die
Kopplungseffekte sehr klein sein werden. Eine Überprüfung im Feld ist nahezu unmöglich, da
Zusammenfassung und Ausblick
74
durch einen Schurf oder durch Probennahme der Boden und damit auch die SIPEigenschaften verändert werden.
Das entwickelte Verfahren zur Korrektur von SIP-Daten kann zukünftig bei der
Auswertung von Messergebnissen eingesetzt werden, um es an möglichst vielen
verschiedenen Datensätzen zu testen, die bei anderen Untergrundbeschaffenheiten
aufgenommen wurden. Ferner kann durch Erweiterung des Programms IP3C (beispielsweise
durch die Einbeziehung variabler Topographien) eine breitere Einsatzmöglichkeit geschaffen
werden.
Ein großer Vorteil des in dieser Arbeit vorgestellten Korrekturverfahrens ist seine
geringe Anforderung an die Rechenleistung. Die Korrekturen können in kurzer Zeit auf
gewöhnlichen PCs durchgeführt werden.
Das Programm IP3C sowie ein Matlab-Programm zur automatischen Korrektur der
Ausgabedateien der SIP256C-Apparatur liegen der Arbeit bei.
Literaturverzeichnis
75
6 Literaturverzeichnis
Althaus, P., 2003, Kontaktlose elektrische Verfahren zur Erkundung des oberflächennahen
Untergrunds und deren Anwendung an Unstetigkeiten durch bergbaubedingte
Bodenbewegungen:
Dissertation,
Fakultät
für
Bergbau,
Hüttenwesen
und
Geowissenschaften der Rheinisch-Westfälischen Technischen Hochschule Aachen.
Blaschek, R., 2006, Aspekte der Inversion von Daten der Spektralen Induzierten Polarisation:
Dissertation, Mathematisch-Naturwissenschaftliche Fakultät der Rheinischen FriedrichWilhelms-Universität Bonn.
Bleil, D. F., 1953, Induced polarization: a method of geophysical prospecting: Geophysics,
18(3), 636-661.
Caglar, I., 2000, A method to remove electromagnetic coupling from induced polarization
data for an “exponential” Earth model: Pure and Applied Geophysics, 157, 1729-1748.
Cole, K. S. & Cole, R. H., 1941, Dispersion and absorption in dielectrics. 1: Alternating
current characteristics: Journal of Chemical Physics, 9, 341-351.
Geotomo Software, 2004, RES2DINV ver. 3.54, rapid 2D resistivity & IP inversion using the
least-squares method: Gelugor, Penang, Malaysia.
Gerthsen, C. & Meschede, D., 2002, Gerthsen Physik: Springer Verlag, Berlin, 305-307.
Hallof, P. G., 1974, The IP phase measurement and inductive coupling: Geophysics, 39(5),
650-665.
Jackson, J. D., 1975, Classical Electrodynamics, 2nd edition, John Wiley & Sons, Inc., New
York, NY.
Klitzsch, N., 2004, Ableitung von Gesteinseigenschaften aus Messungen der spektralen
induzierten Polarisation (SIP) an Sedimentgesteinen: Dissertation, Fakultät für Physik
und Geowissenschaften der Universität Leipzig.
Literaturverzeichnis
76
Kretzschmar, D., 2001, Untersuchungen zur Inversion von spektralen IP-Daten unter
Berücksichtigung
elektromagnetischer
Kabelkopplungseffekte:
Dissertation,
Fachbereich Bauingenieurwesen und Angewandte Geowissenschaften der Technischen
Universität Berlin.
Madden, T. R. & Cantwell, T., 1968, Induced polarisation. A review: Mining Geophysics, 2,
Society of Exploration Geophysicists, Tulsa, OK.
Major, J. & Silic, J., 1981, Restrictions on the use of Cole-Cole dispersion models in complex
resistivity interpretation: Geophysics, 46(6), 916-931
Militzer, H. & Weber, F., 1985, Angewandte Geophysik, Band 2: Geoelektrik, Geothermie,
Radiometrie, Aerophysik: Springer Verlag, Berlin.
Pelton, W. H., Ward, S. H., Hallof, P. G., Sill, W. R. & Nelson, P. H., 1978, Mineral
discrimination and removal of inductive coupling with multifrequency IP: Geophysics,
43(3), 588-609.
Radic, T., 1997, Induzierte Polarisation, in Knödel, K., Krummel, H. & Lange, G.,
Geophysik, Handbuch zur Erkundung des Untergrunds von Deponien und Altlasten,
Band 3: Springer Verlag, Berlin, 166-206.
Schlumberger, C., 1922, Etudes sur la prospection électrique du sous-sol: Gauthier-Villars,
Paris.
Slater, L., 2007, Near surface electrical characterization of hydraulic conductivity: from
petrophysical properties to aquifer geometries - a review: Surveys in Geophysics,
28(2-3), 169-197.
Song, L. A., 1984, New IP decoupling scheme: Exploration Geophysics, 15, 99-112.
Tipler, P. A., 1994, Physik: Spektrum Akademischer Verlag, Heidelberg, Berlin, 698-700.
Telford, W. M., Geldart, L. P. & Sheriff, R. E., 1990, Applied geophysics: Cambridge
University Press, Cambridge.
Literaturverzeichnis
77
van Voorhis, G. D., Nelson, P. H. & Drake, T. L., 1973, Complex resistivity spectra of
porphyry copper mineralization: Geophysics, 38(1), 49-60.
Ward, S. H. & Hohmann, G. W., 1988, Electromagnetic theory for geophysical applications,
in Nabighian, M., Methods in applied geophysics, Band 1: Society of Exploration
Geophysicists, Tulsa, OK, 131-311.
Wong, J., 1979, An electrochemical model of the induced polarization phenomenon in
disseminated sulfide ores: Geophysics, 44(7), 1245-1265.
Zonge, K. C. & Wynn, J. C., 1975, Recent advances and applications in complex resistivity
measurements: Geophysics, 40(5), 851-864.
Anhang
78
7 Anhang
A.1 Der Frequenzeffekt
m=
FE
.
1 + FE
Es folgt:
FE = m + FE ⋅ m
⇔ FE − FE ⋅ m = m
⇔ FE ⋅ (1 − m) = m
m
⇔ FE =
.
1− m
A.2 Das Cole-Cole Modell
R1 + (iωX ) − c + R0
1
1
1
=
+
=
.
Z (ω ) R0 R1 + (iωX ) −c R0 ⋅ R1 + (iωX ) −c
(
)
Es folgt:
R0 ⋅ (R1 + (iωX ) − c )
Z (ω ) =
.
R1 + (iωX ) −c + R0
Ersetzt man:
R0
m :=
R0 + R1
dann folgt:
und
⎛R ⎞
τ := X ⎜ 0 ⎟
⎝m⎠
1
c
= X (R0 + R1 ) c ,
1
Anhang
79
⎛m⎞
X =τ ⋅⎜ ⎟
⎝R⎠
1
c
und
R1 =
R0 − mR0
.
m
Damit ergibt sich:
−c
1
⎛
⎛ m ⎞ c ⎞⎟
⎛ R0 − mR0 ⎞
⎜
R0 ⋅ ⎜
⎟ + R0 ⋅ ⎜ iωτ ⋅ ⎜⎜ ⎟⎟ ⎟
R0 − mR0 (iωτ ) −c ⋅ R0
+
m
⎜
⎝
⎠
⎝ R0 ⎠ ⎟⎠
⎝
m
m
Z (ω ) =
=
−c
−c
1
m
i
1
(
)
ωτ
−
⎛
+
+1
⎛ m ⎞ c ⎞⎟
⎛ R0 − mR0 ⎞ ⎜
m
m
⎜
⎟ + ⎜ iωτ ⋅ ⎜⎜ ⎟⎟ ⎟ + R0
m
⎝
⎠ ⎜
⎝ R0 ⎠ ⎟⎠
⎝
R0 − mR0 + R0 ⋅ (iωτ ) −c
⎛ 1 − m + (iωτ ) −c
⎞
1
−c ⎛
m
⎜
⎟
(
)
R
m
i
R
1
(
)
ωτ
=
=
⋅
−
+
⋅
=
⋅
0
0 ⎜
⎜ 1 + (iωτ ) −c ⎟
⎜ 1 + (iωτ ) −c
1 − m + (iωτ ) −c + m
⎝
⎠
⎝
m
⎛
⎛
⎛ 1 + (iωτ ) −c
⎛ (iωτ ) c ⎞ ⎞
⎛
⎞⎞
m ⎞
1
⎜
⎜
⎟
⎟
⎟⎟ ⎟
⎜⎜
⎜
⎟
R
m
R
m
1
1
=
⋅
−
= R0 ⋅ ⎜⎜
−
=
⋅
−
0 ⎜
0 ⎜
−c
c
⎜ 1 + (iωτ ) −c ⎟ ⎟
⎟
(iωτ ) −c ⎟⎠
⎝
⎠⎠
⎝ 1 + (iωτ )
⎝ (iωτ ) + 1 ⎠ ⎠
⎝
⎝
⎛
⎛
⎞⎞
⎛ (iωτ ) c
⎛ (iωτ ) c + 1 − 1 ⎞ ⎞
1
⎜
⎟
⎟⎟
⎟
⎜⎜
R
m
1
=
⋅
−
−
= R0 ⋅ ⎜⎜1 − m⎜⎜
0 ⎜
c
c
c ⎟⎟
⎟
⎟
⎝ (iωτ ) 1 + (iωτ ) ⎠ ⎠
⎝ (iωτ ) + 1 ⎠ ⎠
⎝
⎝
⎛
⎛
⎞⎞
1
⎟ ⎟.
= R0 ⋅ ⎜⎜1 − m⎜⎜1 −
c ⎟⎟
⎝ 1 + (iωτ ) ⎠ ⎠
⎝
A.3 Der Term Q(R)
∞
iωμ 0 ⎤ 1
I ⎡ u0
−
Q (R ) =
⎢
⎥ J 0 (λR)dλ .
4π ∫0 ⎣ iωε 0
u0 ⎦ λ
Dabei ist u 0 = λ2 − ω 2 μ 0ε 0 . Es folgt:
⎞
⎟⎟
⎠
Anhang
80
2
2
∞
⎤1
iωμ 0
I ⎡ λ − ω μ 0ε 0
⎥ J 0 ( λ R ) dλ
⎢
−
2
2
iωε 0
4π ∫0 ⎢
⎥λ
λ
ω
μ
ε
−
0 0 ⎦
⎣
∞
∞
I ⎡ λ2 − ω 2 μ 0 ε 0 + ω 2 μ 0 ε 0 ⎤ 1
I
λ2
1
⎥
⎢
J
R
d
⋅ J 0 ( λ R ) dλ
(
λ
)
λ
=
=
0
∫
∫
4π ⋅ iωε 0 0 λ2 − ω 2 μ 0ε 0 λ
4π 0 ⎢ iωε 0 ⋅ λ2 − ω 2 μ 0ε 0 ⎥ λ
⎦
⎣
Q (R ) =
∞
=
I
λ
J 0 ( λ R ) dλ .
∫
4π ⋅ iωε 0 0 u 0