15 Verteilungsfunktionen

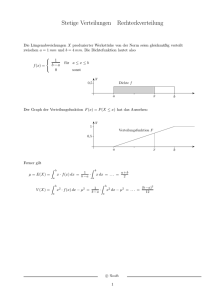
§15 Verteilungsfunktionen
ô
EmpiricalCDF@daten_, z_D := Module@8n<,
n = Length@datenD;
Length@Select@daten, £ z &DD ê n êê ND
In den Kapiteln 13 und 14 haben wir gesehen, dass eine diskrete bzw stetige Verteilung durch ihre
Verteilungsdichte vollständig bestimmt ist. Eine andere, ebenso effiziente Methode, eine Verteilung anzugeben, besteht in der Angabe ihrer Verteilungsfunktion . Eine Unterscheidung in diskrete bzw stetige
Verteilungen ist dabei nicht notwendig. Außerdem lassen sich mit Verteilungsfunktionen auch gemischte
Verteilungen beschreiben.
15.1 Der Begriff Verteilungsfunktion
Ohne auf den Beweis näher eingehen zu können, erwähnen wir den für Verteilungen zentralen Satz
15.1.1 Satz: Ist eine Verteilung, also ein W-Maß auf , so gilt für alle Mengen B Œ ¶
¶
i=1
i=1
@BD = inf 8 ⁄ @D ai , bi DD ˝ B Œ ‹ D ai , bi D<
wobei das Infimum über alle möglichen Überdeckungen der Menge B durch abzählbar viele Intervalle der
Form D ai , bi D zu bilden ist. Die Verteilung ist somit durch Angabe der Wahrscheinlichkeiten @D a, bDD von
Intervallen der Form D a, bD bereits vollständig bestimmt.
Nun lässt sich die Wahrscheinlichkeit @D a, bDD des Intervalls D a, bD aber wegen
@D a, bDD = @D - ¶, bDD - @D - ¶, aDD
durch die Wahrscheinlichkeiten der beiden Intervalle D - ¶, bD und D - ¶, aD ausdrücken. Die Verteilung ist
daher bereits durch Angabe der Wahrscheinlichkeiten @D - ¶, zDD von Intervallen der Form D - ¶, zD vollständig bestimmt.
Wir nehmen diesen Satz zum Anlass und definieren
15.1.2 Definition: Unter der Verteilungsfunktion (im Englischen Cumulative Distribution Function oder kurz
CDF genannt) einer Verteilung versteht man die Abbildung
: Ø @0, 1D mit @zD = @D - ¶, zDD
Wegen Satz 15.1.1 ist die Verteilung durch ihre Verteilungsfunktion vollständig bestimmt.
ô
Wir haben nicht vorausgesetzt, dass die Verteilung diskret bzw stetig sein muss. Der Begriff der Verteilungsfunktion macht nämlich auch dann Sinn, wenn die Verteilung weder diskret noch stetig ist. Für praktische Anwendungen ist dies insbesondere dann von Interesse, wenn es sich bei der Verteilung um eine Verteilung mit diskreten
und stetigen Anteilen (man spricht dabei von einer gemischten Verteilung) handelt.
15.1.3 Bemerkung:
a) Ist eine diskrete Verteilung mit Träger und Verteilungsdichte , so gilt für alle z œ @zD = @D - ¶, zDD = ⁄ @8x<D = ⁄ @xD
xœ
x§z
xœ
x§z
60
@ D
@D
DD
⁄
@8 <D
⁄
15_Verteilungsfunktionen.nb
@ D
Die Verteilungsfunktion einer diskreten Verteilung ist damit eine Stufenfunktion mit den Sprungstellen
z œ und den Sprunghöhen @zD.
b) Ist eine stetige Verteilung mit der Verteilungsdichte , so gilt für alle z œ (differenzielle Denkweise)
@zD = @D - ¶, zDD = Ÿ
z
z
@@x, x + „ xDD = Ÿ @xD „ x
-¶
-¶
Die Verteilungsfunktion einer stetigen Verteilung ist damit eine stetige und stückweise differenzierbare
Funktion mit der Ableitung .
Wir veranschaulichen diese Tatsache graphisch: Die folgende Zeichnung zeigt die Verteilungsdichte (oben)
sowie die zugehörige Verteilungsfunktion (unten) einer diskreten bzw einer stetigen Verteilung . Bei einer
diskreten Verteilung entspricht die Summe der roten Balken der oberen Zeichnung dem roten Balken der unteren
Zeichnung; bei einer stetigen Verteilung entspricht die rot eingezeichnete Fläche der oberen Zeichnung dem roten
Balken der unteren Zeichnung.
@zD
@zD
0.30
0.25
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
z
2
4
6
z
8
@zD
1.0
@zD
1.0
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
2
4
6
8
2
4
6
8
z
2
4
6
z
8
15.1.4 Bemerkung: Ist die Verteilungsfunktion einer Verteilung , so gilt
a) ist monoton nicht abnehmend, d.h. für alle x, y œ mit x < y gilt @xD § @yD;
b) ist rechtsseitig stetig, d.h. für alle z œ gilt limxxz @xD = @zD;
c) ist normiert, d.h. limzØ-¶ @zD = 0 und limzض @zD = 1.
ô
Beweis: a) Für alle x, y œ mit x < y gilt wegen Satz 2.2.2
@xD = @D - ¶, xDD § @D - ¶, yDD = @yD
b) Für alle z œ gilt wegen a) und der Stetigkeit von Wahrscheinlichkeitsmaßen
¶
1
1
lim @xD = lim @D - ¶, xDD = lim @D - ¶, z + DD = @ › D - ¶, z + DD = @D - ¶, zDD = @zD
n
n
nض
x∞z
x∞z
n=1
c) Ebenfalls wegen a) und der Stetigkeit von Wahrscheinlichkeitsmaßen gilt
¶
lim @zD = lim @D - ¶, zDD = lim @D - ¶, -nDD = @ › D - ¶, -nDD = @8 <D = 0
zØ-¶
zØ-¶
nض
n=1
15_Verteilungsfunktionen.nb
61
¶
lim @zD = lim @D - ¶, zDD = lim @D - ¶, nDD = @ ‹ D - ¶, nDD = @D = 1
zض
zض
nض
n=1
Diese drei Eigenschaften sind charakteristisch in dem Sinn, dass jede Funktion : Ø @0, 1D mit diesen Eigenschaften als Verteilungsfunktion einer Verteilung aufgefasst werden kann. Man nennt diese drei Eigenschaften
daher die charakteristischen Eigenschaften einer Verteilungsfunktion.
Für das Rechnen mit Verteilungen ist die folgende Bemerkung von Bedeutung (wir verwenden dabei die Schreibweise @z- D = limxÆz @xD für den linksseitigen Grenzwert der Funktion an der Stelle z):
15.1.5 Bemerkung: Sei eine Verteilung mit der Verteilungsfunktion .
a) Für alle c œ gilt
@8c<D = @cD - @c- D
Die Wahrscheinlichkeit @8c<D der einelementigen Menge 8c< ist somit gleich der Sprunghöhe der Verteilungsfunktion an der Stelle c. Ist die Verteilungsfunktion der Verteilung stetig, so besitzen alle einelementigen Mengen (und damit auch alle Mengen mit abzählbar vielen Elementen) die Wahrscheinlichkeit 0.
b) Für alle a, b œ mit a < b gilt
@D a, bDD = @bD - @aD
@ @a, bDD = @bD - @a- D
@ @a, b@D = @b- D - @a- D
@D a, b@D = @b- D - @aD
ô
15_Verteilungsfunktionen.nb
62
15.2 Verteilungsfunktionen in Mathematica
Mit dem folgenden Befehl lassen sich die Verteilungsfunktionen von in Mathematica implementierten Verteilungen (numerisch und formelmäßig) auswerten:
à CDF@distribution, zD
wertet die Verteilungsfunktion der Verteilung distribution an der Stelle z (sowohl numerisch als auch
formelmäßig) aus. Die Verteilungsfunktionen sowohl von diskreten als auch von stetigen Verteilungen lassen
sich mit dem Befehl Plot zeichnen.
Einige dieser Verteilungsfunktionen verwenden dabei die regularisierte Gamma-Funktion, die regularisierte BetaFunktion sowie die Gauß'sche Fehlerfunktion (diese Funktionen werden in Mathematica mit den Befehlen GammaRegularized bzw BetaRegularized bzw Erf aufgerufen) zur geschlossenen Darstellung von Summen und Integralen. Ohne auf ihre Eigenschaften im Detail einzugehen, definieren wir:
15.2.1 Definition:
a) Unter der regularisierten Gamma-Funktion versteht man die Abbildung
1
y a-1 -t
Gr :D 0, ¶@ µ @0, ¶@ µ@0, ¶@ Ø mit Gr @a, x, yD =
t
‰ „t
G@aD Ÿ x
b) Unter der regularisierten Beta-Funktion versteht man die Abbildung
Br : @0, 1D µ@0, 1D µD 0, ¶@ µD 0, ¶@ Ø mit
Br @x, y, a, bD =
1
y a-1
H1 - tL b-1 „ t
Ÿ t
B@a, bD x
c) Unter der Gauß'schen Fehlerfunktion versteht man die Abbildung
2
z
2
Erf : Ø mit Erf @zD =
Ÿ0 ‰-t „ t
p
ô
Man verwendet oft die Abkürzungen Gr @a, zD = 1 - Gr @a, 0, zD und Br @z, a, bD = Br @0, z, a, bD.
Wir wollen nun die Verteilungsfunktionen der wichtigsten in Mathematica implementierten Verteilungen
analysieren. Unser Ziel besteht dabei wieder darin, diese Verteilungsfunktionen formelmäßig explizit anzugeben
und mit Hilfe von Plot und Manipulate auf dynamische Weise graphisch darzustellen.
15.2.2 Beispiel: Man ermittle die Verteilungsfunktion der diskreten Gleichverteilung @8m, n<D mit den
Parametern m < n œ und zeichne diese Verteilungsfunktion.
ô
15.2.3 Beispiel: Man ermittle die Verteilungsfunktion der Binomialverteilung @n, pD mit den Parametern
n œ und 0 § p § 1 und zeichne diese Verteilungsfunktion.
ô
15.2.4 Beispiel: Man ermittle die Verteilungsfunktion der negativen Binomialverteilung @n, pD mit den
Parametern n œ und 0 § p § 1 und zeichne diese Verteilungsfunktion.
ô
15_Verteilungsfunktionen.nb
15.2.5 Beispiel: Man ermittle die Verteilungsfunktion der Poissonverteilung @lD mit dem Parameter l > 0
und zeichne diese Verteilungsfunktion.
ô
15.2.6 Beispiel: Man ermittle die Verteilungsfunktion der Gleichverteilung @8a, b<D auf dem Intervall @a, bD
und zeichne diese Verteilungsfunktion.
ô
15.2.7 Beispiel: Man ermittle die Verteilungsfunktion der Dreiecksverteilung @8a, b<D auf dem Intervall
@a, bD und zeichne diese Verteilungsfunktion.
ô
15.2.8 Beispiel: Man ermittle die Verteilungsfunktion der Exponentialverteilung @lD mit dem Parameter
l > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.9 Beispiel: Man ermittle die Verteilungsfunktion der Gammaverteilung amma@a, lD mit den Parametern
a > 0 und l > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.10 Beispiel: Man ermittle die Verteilungsfunktion der Laplaceverteilung @a, lD mit den Parametern
a œ und l > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.11 Beispiel: Man ermittle die Verteilungsfunktion der Betaverteilung eta@a, bD mit den Parametern
a > 0 und b > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.12 Beispiel: Man ermittle die Verteilungsfunktion der Normalverteilung @m, sD mit den Parametern
m œ und s > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.13 Beispiel: Man ermittle die Verteilungsfunktion der logarithmischen Normalverteilung @m,sD mit
den Parametern mœ und s>0 und zeichne diese Verteilungsfunktion.
ô
15.2.14 Beispiel: Man ermittle die Verteilungsfunktion der Chi-Quadrat Verteilung hi@nD mit dem Parameter
n œ und zeichne diese Verteilungsfunktion.
ô
15.2.15 Beispiel: Man ermittle die Verteilungsfunktion der Student T Verteilung @nD mit dem Parameter
n œ und zeichne diese Verteilungsfunktion.
ô
63
15_Verteilungsfunktionen.nb
64
15.2.16 Beispiel: Man ermittle die Verteilungsfunktion der Fisher F Verteilung @m, nD mit den Parametern
m, n œ und zeichne diese Verteilungsfunktion.
ô
15.2.17 Beispiel: Man ermittle die Verteilungsfunktion der Weibullverteilung @a, bD mit den Parametern
a > 0 und b > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.18 Beispiel: Man ermittle die Verteilungsfunktion der Extremwertverteilung xtrem@m, bD mit den
Parametern m œ und b > 0 und zeichne diese Verteilungsfunktion.
ô
15.2.19 Beispiel: Man ermittle die Verteilungsfunktion der Rayleighverteilung @sD mit dem Parameter s > 0
und zeichne diese Verteilungsfunktion.
ô
15.3 Verteilungsfunktionen von Zufallsvariablen
Bisher haben wir uns nur mit den Verteilungsfunktionen von Verteilungen beschäftigt. In diesem Abschnitt
befassen wir uns mit den Verteilungsfunktionen Z von Zufallsvariablen Z.
15.3.1 Definition: Unter der Verteilungsfunktion Z einer Zufallsvariablen Z versteht man die Verteilungsfunktion der Verteilung Z von Z, also die Abbildung
Z : Ø @0, 1D mit Z @zD = @8Z § z<D
Wegen Bemerkung 15.1.3 ist die Verteilung Z der Zufallsvariablen Z durch ihre Verteilungsfunktion Z
bereits vollständig bestimmt.
An Hand von einigen Beispielen werden wir nun zeigen, wie sich die Verteilungsfunktion Z einer Zufallsvariablen
Z ermitteln lässt, wobei wir uns zunächst nochmals mit den bereits in den Abschnitten 13.3 und 14.3 behandelten
Zufallsvariablen, deren Verteilungsdichten wir bereits ermittelt haben, befassen werden. Wir werden die auf diese
Weise ermittelten Verteilungsfunktionen jeweils Mathematica-gerecht aufbereiten und zeichnen.
15.3.2 Beispiel: Unser Zufallsexperiment besteht im Werfen von zwei homogenen Würfeln. Mit der
Zufallsvariablen Z wird die dabei auftretenden Augensumme bezeichnet. Man analysiere die
Verteilungsfunktion Z von Z.
ô
Lösung: In Beispiel 13.3.3 haben wir die Verteilungsdichte Z @zD der Zufallsvariablen Z bereits ermittelt
Hz - 1L ê62
Z @zD = @8Z = z<D = H13 - zL ë 62
0
und Mathematica-gerecht aufbereitet:
für z œ 82, 3, ..., 7<
für z œ 88, 9, ..., 12<
sonst
15_Verteilungsfunktionen.nb
65
fd1@z_D := 0 ê; Or@z < 2, z > 12, NumberQ@zD && Not@IntegerQ@zDDD
fd1@z_D := Hz - 1L í 62 ê; 2 £ z £ 7;
fd1@z_D := H13 - zL í 62 ê; 8 £ z £ 12;
Wegen Bemerkung 15.1.3
FullSimplify@Sum@fd1@iD, 8i, 2, z<DD
FullSimplifyBSumBHi - 1L í 62 , 8i, 2, z<FF
FullSimplifyBSumBH13 - iL í 62 , 8i, 8, z<FF
z
‚ fd1@iD
i=2
1
72
H−1 + zL z
1
−
72
H−18 + zL H−7 + zL
besitzt diese Zufallsvariable Z damit die Verteilungsfunktion
für z < k
0
Z @zD =
zHz-1L
dzt
⁄i=2 Z @iD =
72
1
dzt
H42 + H18 - zL Hz - 7LL
⁄i=2 Z @iD =
72
für 2 § z < 7
für 7 § z < 12
für z ¥ 12
1
Diese Verteilungsfunktion lässt sich mittels Piecewise mühelos in Mathematica eingeben
Fd1@z_D := Piecewise@88z Hz - 1L ê 72, 2 £ z < 7<, 81 ê 72 H42 + H18 - zL Hz - 7LL, 7 £ z < 12<, 81, z ≥ 12<<D
und für beliebige Werte von k und n auf dynamische Weise graphisch darstellen:
Plot@Fd1@zD, 8z, -2, 20<, PlotPoints Æ 200,
AspectRatio Æ 0.4, PlotStyle Æ [email protected], AxesOrigin Æ 8-1, 0<, PlotRange Æ All,
AxesLabel Æ 8"z", "@zD"<, ImageSize Æ 8200, 100<D
@zD
1.0
0.8
0.6
0.4
0.2
0
5
10
15
20
z
15.3.3 Beispiel: Durch einen Kanal werden n unabhängige Kodeworte übertragen. Die Wahrscheinlichkeit
dafür, dass das Kodewort richtig empfangen wird, ist 0.9. Mit der Zufallsvariablen Z wird die Anzahl der
Kodeworten, die richtig empfangen wurden, bezeichnet. Man analysiere die Verteilungsdichte Z von Z. Man
analysiere die Verteilungsfunktion Z von Z.
ô
15_Verteilungsfunktionen.nb
66
Lösung: In Beispiel 13.3.5 haben wir die Verteilungsdichte Z @zD, z œ Z = 81, 2, …, n< der Zufallsvariablen Z
bereits ermittelt
Z @zD = @8Z = z<D =
K
n
O 0.9 z 0.1n-z für z œ Z
z
sonst
0
und Mathematica-gerecht aufbereitet:
fd1@z_, n_, p_D := 0 ê; Or@z < 1, z > n, NumberQ@zD && Not@IntegerQ@zDDD
fd1@z_, n_, p_D := Binomial@n, zD p ^ z H1 - pL ^ Hn - zL
Wegen Bemerkung 15.1.3
besitzt diese Zufallsvariable Z damit die Verteilungsfunktion
0
p i
dzt
dzt n
Z @zD = ⁄i=1 Z @iD = H1 - pLn ⁄i=1 K i O
1- p
1
für z < k
für 1 § z < n
für z ¥ n
Diese Verteilungsfunktion lässt sich mittels Piecewise mühelos in Mathematica eingeben
Fd1@z_, n_, p_D := PiecewiseB::H1 - pLn SumBBinomial@n, iD
p
1-p
i
, 8i, 1, z<F, 1 £ z < n>, 81, z ≥ n<>F
und für beliebige Werte von k und n auf dynamische Weise graphisch darstellen:
Manipulate@ListPlot@Table@8z, Fd1@z, n, pD<, 8z, 1, 50<D,
PlotStyle Æ [email protected], Filling Æ Axis, AspectRatio Æ 0.4, AxesOrigin Æ 8-1, 0<, PlotRange Æ All,
AxesLabel Æ 8z, @zD<, ImageSize Æ 8200, 100<D,
8n, 1, 50, 1, Appearance Æ "Labeled"<, 8p, 0, 0.99, Appearance Æ "Labeled"<D
n
40
p
0.601
Nach diesen Beispielen über Verteilungsfunktionen von diskreten Zufallsvariablen befassen wir uns nun mit
Beispielen über Verteilungsfunktionen von stetigen Zufallsvariablen.
15.3.4 Beispiel: Aus dem Intervall @0, 1D werden zufällig n Zahlen ausgewählt und ihr Minimum Z
beobachtet. Man analysiere die Verteilungsfunktion Z von Z.
15_Verteilungsfunktionen.nb
67
ô
Lösung: In Beispiel 14.3.2 haben wir die Verteilungsdichte Z dieser Zufallsvariablen Z bereits ermittelt
Z @zD =
n H1 - zL n-1
0
für 0 § z § 1
sonst
und Mathematica-gerecht aufbereitet:
fs1@z_, n_D := Piecewise@88n H1 - zLn-1 , 0 £ z £ 1<<D
Wegen Bemerkung 15.1.3 und
Fs1@z_, n_D := Evaluate@Integrate@fs1@z, nD, zDD; Fs1@z, nD
0
z≤0
1 − H1 − zLn 0 < z ≤ 1
0
True
(das Integral muss zuerst mit Hilfe von Evaluate ausgewertet werden, bevor damit weitere Berechnungen angestellt
werden können) gilt damit
für z < 0
für 0 § z < 1
für z ¥ 1
0
z
Z @zD = Ÿ 0 Z @xD „ x = 1 - H1 - zLn
1
Man hätte diese Verteilungsfunktion natürlich auch direkt berechnen können. Für alle 0 § z < 1 gilt nämlich
Z @zD = @8Z § z<D = 1 - @8Z > z<D = 1 - @8alle n Punkte liegen rechts von z<D = 1 - H1 - zLn
Diese Verteilungsfunktion lässt sich nun für beliebige Werte von n auf dynamische Weise graphisch darstellen:
Manipulate@Plot@Fs1@z, nD, 8z, -0.1, 1.1<, AspectRatio Æ 0.4, PlotStyle Æ [email protected],
AxesOrigin Æ 8-0.1, 0<, PlotRange Æ All, AxesLabel Æ 8"z", "@zD"<, ImageSize Æ 8200, 100<D,
8n, 1, 10, 1, Appearance Æ "Labeled"<D
n
6
@zD
1.0
0.8
0.6
0.4
0.2
0.0
0.2
0.4
0.6
0.8
1.0
z
15.3.5 Beispiel: Ein Punkt wird zufällig in den ersten Quadrant des Einheitskreises geworfen und seine xKoordinate Z bestimmt. Man ermittle die Verteilungsfunktion Z von Z.
ô
15_Verteilungsfunktionen.nb
68
Lösung: In Beispiel 14.3.3 haben wir die Verteilungsdichte Z dieser Zufallsvariablen Z bereits ermittelt
Z @zD =
1
@8Z œ @z, z + „ zD<D =
„z
4
p
0
1 - z2
für 0 § z § 1
sonst
und Mathematica-gerecht aufbereitet:
fs2@z_D := Piecewise@884 Sqrt@1 - z2 D ê p, 0 £ z £ 1<<D
Wegen Bemerkung 15.1.3 und
Fs2@z_D := Evaluate@Integrate@fs2@zD, zDD; Fs2@zD
z≤0
0
2 z
1−z2 +ArcSin@zD
0<z≤1
π
1
True
gilt damit
für z < 0
0
2
z
Z @zD = Ÿ Z @xD „ x = Hz
0
p
1
1 - z2 + ArcSin@zDL
für 0 § z < 1
für z ¥ 1
Diese Verteilungsfunktion lässt sich natürlich mühelos zeichnen:
Plot@Fs2@zD, 8z, -0.1, 1.2<, PlotStyle Æ [email protected], AspectRatio Æ 0.4, AxesOrigin Æ 8-0.1, 0<,
PlotRange Æ All, AxesLabel Æ 8"z", "@zD"<D
@zD
1.0
0.8
0.6
0.4
0.2
0.0
0.2
0.4
0.6
0.8
1.0
1.2
z
15.3.6 Beispiel: Auf der unteren und der linken Seitenkante eines Quadrats der Seitenlänge 1 werden
willkürlich zwei Punkte P und Q ausgewählt. Man ermittle die Verteilungsfunktion Z ihres Abstandes Z.
ô
Lösung: In Beispiel 14.3.4 haben wir die Verteilungsdichte Z @zD dieser Zufallsvariablen Z bereits ermittelt
z pê2
Z @zD = z pê2 - 2 z ArcTan @
0
für 0 § z < 1
z2 - 1 D
für 1 § z §
sonst
2
und Mathematica-gerecht aufgereitet:
fs3@z_D := Piecewise@88z p ê 2, 0 £ z £ 1<, 8z p ê 2 - 2 z ArcTan@Sqrt@z2 - 1DD, 1 £ z £ Sqrt@2D<<D
Wegen Bemerkung 15.1.3 und
15_Verteilungsfunktionen.nb
69
Fs3@z_D := Evaluate@Integrate@fs3@zD, zDD; Fs3@zD
z≤0
0
π z2
4
π z2
0<z≤1
+
−1 + z2 − z2 ArcTanB
4
−1 + z2 F 1 < z ≤
1
2
True
gilt damit
für z < 0
0
Z @zD =
z
Ÿ 0 Z @xD „ x = z2 pê4
z
2
Ÿ 0 Z @xD „ x = z pê4 + H
für 0 § z < 1
z2 - 1 - z2 ArcTan@
z2 - 1 DL
für 1 § z <
für z ¥
1
2
2
Diese Verteilungsfunktion lässt sich wieder mühelos zeichnen:
Plot@Fs3@zD, 8z, -0.2, 1.7<, PlotStyle Æ [email protected], AspectRatio Æ 0.4, AxesOrigin Æ 8-0.2, 0<,
PlotRange Æ All, AxesLabel Æ 8z, Z @zD<D
Z HzL
1.0
0.8
0.6
0.4
0.2
z
0.0
0.5
1.0
1.5
15.3.7 Beispiel: n Punkte werden zufällig in den Einheitskreis geworfen und der Abstand Z vom Mittelpunkt
des Einheitskreises zum nächst gelegenen dieser n Punkte beobachtet. Man ermittle die Verteilungsfunktion
Z von Z.
ô
Lösung: In Beispiel 14.3.5 haben wir die Verteilungsdichte Z @zD dieser Zufallsvariablen Z bereits ermittelt
2 n-1
Z @zD = ; 2 n z H1 - z L
0
für 0 § z § 1
sonst
und Mathematica-gerecht aufbereitet:
fs4@z_, n_D := Piecewise@882 n z H1 - z2 Ln-1 , 0 £ z £ 1<<D
Wegen Bemerkung 15.1.3 und
Fs4@z_, n_D := Evaluate@Integrate@fs4@z, nD, zDD; Fs4@z, nD
z≤0
1 − I1 − z2 Mn 0 < z ≤ 1
0
0
gilt damit
True
15_Verteilungsfunktionen.nb
70
0
z
2
Z @zD = Ÿ Z @xD „ x = 1 - H1 - z Ln
0
1
für z < 0
für 0 § z < 1
für z ¥ 1
Man hätte diese Verteilungsfunktion auch wieder direkt berechnen können. Für alle 0 § z < 1 gilt nämlich
Z @zD = @8Z § z<D = 1 - @8Z > z<D = 1 - @:
alle n Punkte liegen nicht im Kreis
>D = 1 - H1 - z2 Ln
mit Mittelpunkt 80, 0< und Radius z
Diese Verteilungsfunktion lässt sich wieder für beliebige Werte von n auf dynamische Weise graphisch darstellen:
Manipulate@Plot@Fs4@z, nD, 8z, -0.1, 1.1<,
PlotStyle Æ [email protected], AspectRatio Æ 0.4, AxesOrigin Æ 8-0.1, 0<, PlotRange Æ All,
AxesLabel Æ 8"z", "@zD"<, ImageSize Æ 8200, 100<D,
8n, 1, 20, 1, Appearance Æ "Labeled"<D
n
3
@zD
1.0
0.8
0.6
0.4
0.2
0.0
0.2
0.4
0.6
0.8
1.0
z
15.3.8 Beispiel: Der Punkt P sei auf der Oberfläche der Einheitskugel gleichverteilt. Man ermittle die
Verteilungsfunktion des Winkels Q, den der Ortsvektor OP zum Punkt P mit der z-Achse einschließt.
ô
In manchen Fällen kann es sinnvoll sein, die Verteilungsfunktion einer Zufallsvariablen durch Simulation
näherungsweise zu ermitteln. Man erzeugt dazu eine genügend große Anzahl (vergleiche dazu unsere Faustregel)
von Realisierungen dieser Zufallsvariablen Z und ermittelt von diesem Datenmaterial daten unter Verwendung des
Befehls EmpiricalCDF die empirische Verteilungsfunktion. Für alle z œ stellt die empirische Verteilungsfunktion
`
Z @zD = relative Häufigkeit des Intervalls D - ¶, zD im Datenmaterial daten
eine gute Näherung für die gesuchte Verteilungsfunktion der Zufallsvariablen Z an der Stelle z dar. Man beachte
wieder, dass sich die auf diese Weise ermittelte empirische Verteilungsfunktion von Simulationslauf zu Simulationslauf geringfügig ändern wird.
à EmpiricalCDF@daten, zD
ordnet jedem z œ die relative Häufigkeit des Intervalls D - ¶, zD im Datenmaterial daten zu.
15_Verteilungsfunktionen.nb
15.3.9 Beispiel: Aus einer Urne mit s = 8 schwarzen, r = 6 roten und g = 4 grünen Kugeln werden so lange
Kugeln gezogen und nach jedem Zug wieder zurückgelegt, bis erstmals hintereinander zwei gleich gefärbte
Kugeln gezogen werden. Die Zufallsvariable Z gibt an, wieviele Züge dafür notwendig sind. Man ermittle die
Verteilungsfunktion Z von Z.
ô
71
15_Verteilungsfunktionen.nb
72
15.3.10 Beispiel: Aus dem Intervall @0, 1D werden zufällig drei Zahlen ausgewählt. Man ermittle die
`
empirische Verteilungsfunktion Z ihrer Summe Z.
ô