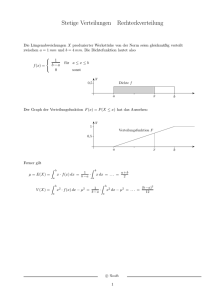
Gesammelte Fragen zur Übung aus den Vorjahren

Ich habe eine Frage zur Tschebyschew Ungleichung. In der Aufgabe 4 des Übungsblattes 3 benötigt man ja die Ungleichung. In diesem Falle war der Bereich (10, 20)
symmetrisch um den Erwartungswert µ = 15. Wie berechnet man die Wahrscheinlichkeit nun, wenn die Wahrscheinlichkeit für das beobachtete Intervall asymmetrisch um den Erwartungswert ist? Also in diesem speziellen Fall der Erwartungswert z.B. 16 wäre?
Antwort:
Die Ungleichung von Tschebyschew wird dafür verwendet, eine Wahrscheinlichkeit abzuschätzen, nämlich die Wahrscheinlichkeit, dass die Realisation
einer Zufallsvariablen X ausserhalb eines symmetrischen Intervalls um den
Erwartungswert: [µ − c; µ + c] liegt. Die Ungleichung lautet:
P(|X − µ| ≥ c) ≤
Var(X)
c2
mit
|X − µ| ≥ c ⇔ (X ≤ µ − c) ∨ (X ≥ µ + c)
In der Übung wurde eine alternative, äquivalente Formulierung verwendet:
P(|X − µ| < c) ≥ 1 −
Var(X)
c2
Beim gegebenen Intervall [10; 20] und µ = 16 wäre die Ungleichung also
nicht anwendbar.
Man kann aber mit c = 4 die Wahrscheinlickeit für das Intervall [12; 20]
abschätzen:
P(12 ≤ X ≤ 20) = P(|X − 16| ≤ 4) ≥ 1 −
4
3
Var(X)
=1−
= = 0,75
2
c
16 4
Nachtrag: Die obige Gleichung stellt eigentlich bereits eine Abschätzung für P(10 ≤
X ≤ 20), denn es gilt ja , dass P(10 ≤ X ≤ 20) ≥ P(12 ≤ X ≤ 20). Man
kann also folgende Abschätzung anstellen:
P(10 ≤ X ≤ 20) ≥ P(12 ≤ X ≤ 20) = P(|X − 16| ≤ 4) ≥ . . . = 0,75
1
Ich habe eine Frage zum Übungsblatt 2, Aufgabe 3: Warum kann ich hier nicht
einfach die Wahrscheinlichkeiten multiplizieren, mit denen das Brot nicht okay
ist, also 0,1 mal 0,05 mal 0,2 mal 0,15, also die Schnittmenge der Wahrscheinlichkeiten, dass das Mehl Mängel hat?
Antwort:
P(E 1 ∩ E 2 ∩ E 3 ∩ E 4 ) ist die Wahrscheinlichkeit dafür, dass keine Mehlsorte einwandfrei ist. Das Brot kann jedoch nicht verkauft werden, wenn
mindestens eine Mehlsorte nicht einwandfrei ist. Gesucht ist also die Wahrscheinlichkeit, dass Mehlsorte 1 oder Mehlsorte 2 oder Mehlsorte 3 oder
Mehlsorte 4 Mängel hat.
Das interessierende Ereignis ist somit die Vereinigungsmenge der Ereignisse E i und nicht deren Schnittmenge.
P(B)
=
DeMorgan
=
Folgerung1
=
=
P(E 1 ∪ E 2 ∪ E 3 ∪ E 4 )
P E1 ∩ E2 ∩ E3 ∩ E4
1 − P(E1 ∩ E2 ∩ E3 ∩ E4 )
1 − P(B)
1
Uns hat sich eine Frage zum Übungsblatt 3, Aufgabe 2a) ergeben. Könnten Sie
uns sagen, welche der Lösungen richtig ist?
Dichtefunktion:
oder:


0
für x ≤ 2




 1
f (x) = 
− x + 2 für 2 ≤ x ≤ 4




 02
für x > 4


0
für x < 2




 1
f (x) = 
− x + 2 für 2 ≤ x ≤ 4




 02
für x > 4
weil die 2 kann ja nur bei einem von beiden eingeschlossen sein?
Antwort:
Die zweite Dichtefunktion ist richtig. Sie ergibt sich als erste Ableitung der Verteilungsfunktion von X:


0
für x < 2




 1 2
F(x) = 
− x + 2x − 3 für 2 ≤ x ≤ 4




 14
für x > 4
Der Definition einer Abbildung nach wird jedem Element im Definitionsbereich
genau ein Element im Wertebereich zugeordnet. Die 2 kann also nur in einem der
angegebenen Intervallen enthalten sein.
1
Bei Aufgabe 3a Blatt 1 ist mir die Lösung klar! Jedoch wollte ich fragen, wie man
folgenden Fall berechnet: „mindestens (statt genau) 3 Ober und genau 2 Unter“?
Wäre die Lösung dann : 4 aus 4 = alle Ober x 2 aus 4 Unter x 2 aus 24 Restkarten?
Antwort:
Die vorgeschlagene Lösung:
! ! !
4 4 24
= 1 · 6 · 276 = 1656
4 2 2
entspricht der Anzahl der Hände, in denen der Spieler unter seinen 8 Karten genau
4 Ober und genau 2 Unter besitzt.
Die Frage lautet aber „mindestens (statt genau) 3 Ober und genau 2 Unter“, d.h.
entweder „genau 3 Ober und genau 2 Unter“ oder „genau 4 Ober und genau 2
Unter“.
Diese Anzahl beträgt:
! ! !
! ! !
4 4 24
4 4 24
+
= 48576 + 1656 = 50232.
3 2 3
4 2 2
1
Ich hätte eine allgemeine Verständnisfrage zum Blatt 5. Und zwar steht in der
Aufgabe 3: Varianz σ2 = 7,42 . Ist die Varianz nun 7,4 oder 54,76? In Aufgabe 4
kommt dann auch nochmal "Varianz unabhängig davon immer 4". Schreibt man
dann auch Varianz=22 oder 42 ?
Antwort:
2
2
Bei Aufgabe√3 ist die
p Varianz σ = 7,4 = 54,76 und somit die Standardabweichung σ = σ2 = 7,42 = 7,4.
Bei Aufgabe 4 ist die Varianz σ2 = 4 = 22 und die Standardabweichung σ = 2.
1
Ich versuche gerade die Lösung von Übungsblatt 5 Aufgabe 1, wie wir sie in der
Übung aufgeschrieben haben, nach zu vollziehen. Dabei stellt sich mir folgende
Frage: Wieso arbeiten wir plötzlich mit f(t) und nicht mit f(x), wurde hier etwas
substituiert? Außerdem ist mir nicht klar, wieso beim Integeral für x > 0 man
nochmal komplett von −∞ bis x integriert anstatt von 0 bis x, wurde das nicht
oben bereits bei x < 0 abgehandelt?
Antwort:
Die Verteilungsfunktion einer Zufallsvariablen X ist definiert durch
F(x) = P(X ≤ x) = P(−∞ < X ≤ x)
Die Verteilungsfunktion einer stetigen Zufallsvariablen ermittelt sich über das Integral der Dichtefunktion im Intervall ] − ∞; x ] (Vgl. Folie 12.16).
Z x
F(x) =
f (u)du
−∞
Die Verteilungsfunktion F ist eine Funktion der Variablen x. Für die Dichtefunktion f im Integrand muss eine neue Variable z.B u oder t eingeführt werden, da x
als obere Integrationsgrenze vorkommt.
Die Dichtefunktion der Exponentialverteilung lautet:
(
λ exp(−λx), für x ≥ 0
f (x) =
0
für x < 0
Um die Verteilungsfuntion der Exponentialverteilung zu bestimmen, muss man,
der Definition der Dichtefunktion entsprechend, zwei Fälle unterscheiden:
• x < 0:
F(x) =
=
Zx
−∞
Zx
−∞
1
f (u)du
0 du = 0
• x ≥ 0:
F(x) =
=
=
Zx
−∞
Z0
−∞
Zx
f (u)du
f (u)du +
Zx
f (u)du
0
λ exp(−λu)du +
Zx
λ exp(−λu)du
0
−∞
In beiden Fällen wird die Verteilungsfuktion über das Integral der Dichtefunktion
im Intervall ] − ∞; x ] ermittelt. Man könnte hier natürlich das Integral von −∞
bis 0 weglassen, da man ja gezeigt hat, dass dies immer 0 ist. Hier ist die Notation
aber bewusst etwas allgemeiner gehalten. Es könnte ja auch Dichten geben, die
ebenfalls auf Teilbereichen von x unterschiedlich definiert sind, bei denen aber in
mehreren Teilbereichen von x die Dichte größer als Null ist. Und in so einem Fall
wäre das natürlich zu berücksichtigen.
Bemerkung:
Das Beispiel zur Verteilungsfunktion der Gleichverteilung in der Vorlesung vom
29.04. (Video: 53:50 - 55:60) kann in diesem Zusammenhang auch hilfreich sein.
2
Ich habe eine Frage zum Übungsblatt 4, Aufgabe 2: Dort hatten wir die Formel
für den sog. „Spezialfall“ benutzt. Ich gehe davon aus, dass dieser „Spezialfall“
deswegen hergenommen wurde, da nur ganze Zahlen von 1-12 (12 = k) bei dem
Würfel vorhanden sind.
Wäre jetzt auf dem Würfel eine „0“ oder zwei mal eine „5“ z.B. (natürlich sehr
theoretisch), dürfte man die Formel für den Erwartungswert und die Varianz nicht
hernehmen, wie sie auch im Skript steht?!
Welche Formel würde dann zum Tragen kommen?
Antwort:
Die Wahrscheinlichkeitsfunktion der diskreten Gleichverteilung lautet:
1
für i = 1, . . . ,k .
k
Im Spezialfall xi = i sind die k Ausprägungen der Zufallsvariable die ersten k
natürlichen Zahlen.
Bei der Aufgabe hat die Zufallsvariable X, welche die „Augenzahl beim einmaligen Würfeln mit einem Dodekaeder“ beschreibt, zwölf Ausprägungen, nämlich:
x1 = 1 , x2 = 2, x3 = 3, . . . , x11 = 11, x12 = 12.
1
.
Jede Ausprägung xi = i hat die gleiche Wahrscheinlichkeit: 12
P(X = xi ) =
Würde die „5“ zweimal vorkommen, dann würde keine diskrete Gleichverteilung
2
mehr vorliegen, denn es würde gelten: P(X = 5) = 12
.
Für beliebige, unterschiedliche k Ausprägungen verwendet man die allgemeinen
Formeln für den Erwartungswert und die Varianz, also:
E(X) =
k
X
i=1
k
X
x i · pi =
Var(X) =
=
i=1
1 1X
=
xi .
k k i=1
k
X
(xi − E(X))2 · pi
i=1
k
X
i=1
=
k
xi ·
(xi − E(X))2 ·
k
1
k
1X
(xi − E(X))2
k i=1
1
Ich habe eine Frage zur Aufgabe 3a in Blatt 4. Leider wurde es in der Vorlesung
nur sehr kurz besprochen und auch im Skript verwirrt mich die Zusammenstellung
etwas. Inwiefern stehen „Bernoulli-Experiment“ und „Binomialverteilung“ zueinander? So wie ich das verstanden habe, bedeutet Bernoulli-Experiment, dass es
nur max. 2 mögliche Ausprägungen „Überraschung“ und „Nicht Überraschung“
gibt. Binomialverteilung heißt dann, dass bei jedem Bernoulli-Experiment (also bei jedem Kauf einer Keksschachtel) die gleiche Wahrscheinlichkeit für eine
Überraschung (also 1/6 - da in jeder 6. Schachtel eine Überraschung sein soll)
besteht und dass das Ergebnis der Wahrscheinlichkeit die Überraschungen sind?!
Anschlussfrage: Was bedeutet die Formel für Bernoulli : X ∼ B(1,p) und im Gegenzug X ∼ B(n,p)?
Vor allem auch das B lässt mich bisher etwas rätseln.
Antwort:
Jeder Kauf einer Schachtel ist ein Bernoulli-Experiment (Vgl. Folie 13.9 und Vorlesung vom 13.05. Video: 3:18 - 7:00). Mit Wahrscheinlichkeit p = 1/6 findet
man in der Schachtel eine Überraschung (Erfolg) und mit Wahrscheinlichkeit
(1 − p) = 5/6 findet man keine Überraschung (Misserfolg).
Nun wird dieses Bernoulli-Experiment n = 20 Mal wiederholt, wobei die Wiederholungen unabhängig voneinander sind. Das bedeutet, dass die Erfolgswahrscheinlichkeit (p = 1/6) bei jeder Wiederholung konstant gleich bleibt.
(
1 falls „Überraschung“
Zi =
i = 1, . . . , 20.
0 falls „keine Überraschung“
Zi ∼ B(n = 1, p = 1/6)
Man interessiert sich nun für die Anzahl der Erfolge, also für die Anzahl der
Schachteln, bei denen man eine „Überraschung“ findet. Diese Anzahl ist binomialverteilt (Vgl. Folie 13.14 und Videoaufzeichung: 11:00 - 13:06).
X: „Anzahl der Keksschachteln mit Überraschung“
X ∼ B(n = 20, p = 1/6)
Die Binomialverteilung ergibt sich, wenn aus n unabhängigen Wiederholungen
eines Bernoulli-Experiments mit konstanter Wahrscheinlichkeit p die Summe der
Erfolge gebildet wird.
Zi ∼ B(1, p)
X=
n
X
i=1
Zi ∼ B(n,p)
Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung. Das B steht
für „Binomial“. Bei der Bernoulli-Verteilung ist n = 1.
1
Ich hätte eine Frage, die sich auf das Übungsblatt 6 bezieht.
Dort haben wir ja in Aufgabe 3 und 4 allgemein hergeleitet, dass der ML-Schätzung
für die jeweiligen Parameter λ und p der Poisson- und der Binomialverteilung dem
arithmetischen Mittel entspricht.
Da das aber ja nicht allgemein der Fall ist, würde mich einfach interessieren, bei
welchen der (von uns behandelten) Verteilungen das denn noch so ist.
Antwort:
Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung (n = 1). Bei
dieser Verteilung ist x̄ ebenfalls der ML-Schätzer für den Parameter p.
Bei der Normalverteilung ist das arithmetische Mittel der ML-Schätzer für den
Erwartungswert µ. Dies wurde auch in der Vorlesung hergeleitet (Vgl. Videoaufzeichnung zu Kapitel 14: 57:8-66:26).
1
Bei Blatt 5 ist in Aufgabe 1 die Rede von der Exponentialverteilung. Bei der
Verteilungsfunktion ist mir folgendes aufgefallen. Wie kann ich ein Integral von
„ - unendlich“ bis „x“ spannen, wenn ich hierbei die „x“ alle in "t“ umwandle?
Wozu das alles und warum heißt es dann nicht „ - unendlich bis t“?
Antwort:
Die Verteilungsfunktion einer Zufallsvariablen X ist definiert durch
F(x) = P(X ≤ x) = P(−∞ < X ≤ x)
Die Verteilungsfunktion einer stetigen Zufallsvariablen ermittelt sich über das Integral der Dichtefunktion im Intervall ] − ∞; x ] (Vgl. Folie 12.16).
Z x
F(x) =
f (u)du
−∞
Die Verteilungsfunktion F ist eine Funktion der Variablen x. Für die Dichtefunktion f im Integrand muss eine neue Variable z.B u oder t eingeführt werden, da x
als obere Integrationsgrenze vorkommt. Es wird also nichts umgewandelt.
In der Vorlesung vom 29.04. (Video: 53:50 - 55:60) wurde ein Beispiel zur Verteilungsfunktion der Gleichverteilung vorgerechnet. Man kann an diesem Beispiel
die Herangehensweise bei der Ermittlung der Verteilungsfuktion einer stetigen
Zufallsvariablen gut nachvollziehen.
Die Antworten auf Frage 14 und Frage 19 sind ebenfalls eine gute Ergänzung.
1
Mir ist die komplette Aufgabe 1 auf Blatt 5 recht unklar. Es ergeben sich bei mir
mehrere Fragen.
a) Warum wird die Dichtefunktion f(x) auf einmal in f(t) umgewandelt?
b) Warum ist bei der Integralrechnung die obere Grenze noch „x“ und nicht
„t“, wenn es umgewandelt wird?
c) Bei der Fallunterscheidung wurden dann 2 Integralrechnungen gemacht.
Beim Fall für x (warum nicht t?) >= 0 wurde dann eine Addition zweier
Grenzen gemacht. Die erste Grenze geht dabei von minus unendlich bis 0.
Hier schon die Frage, warum bis 0? Es muss eigentlich bis −1 gehen, da die
0 ja gar nicht in der Grenze des Falles für x < 0 ist! Dies addiert mit der
Grenze 0 bis x (warum nicht t?), was mir wiederum klar ist. Da ja sowohl
die 0 als auch das Ergebnis x (was ja nun t ist?!) im einen Fall sind.
Antwort:
Zu a) und b) siehe Antworten auf Frage 14 und Frage 18.
Zu c): Hier wird folgende Eigenschaft des bestimmten Integrals verwendet:
Rb
Rc
Rc
f (t)dt + f (t)dt = f (t)dt, wenn a < b < c.
a
b
a
Mit a = −∞, b = 0 und c = x ergibt sich für den Fall: x ≥ 0:
F(x) =
=
=
Zx
−∞
Z0
−∞
Zx
f (t)dt
f (t)dt +
Zx
f (t)dt
0
λ exp(−λt)dt +
Zx
0
−∞
1
λ exp(−λt)dt
Ich habe eine Frage zum ersten Übungsblatt, 1. Aufgabe.
„Bei einer Party mit 10 Gästen umarmt zur Begrüßung jeder jeden. Wie viele
Umarmungen gibt es dann?“
Als Lösung haben wir aufgeschrieben, dass es eine Kombination ist und somit 102
Ich hätte eigentlich gedacht, dass es sich hier um eine Permutation handelt, da
ja nach der Anzahl der Umarmungen gefragt wird. Und man ja nicht „2 aus 10“
auswählt und wissen will wie viele Kombinationen dafür möglich sind? Meine
Lösung wäre dann wohl 9! gewesen. (Der erste umarmt 9, der nächste nur noch 8,
der nächste nur noch 7. . . .)
Wie so wird hier eine Kombination statt einer Permutation genommen?
Antwort:
Es wird nach der Anzahl an überhaupt stattfindenden Umarmungen gefragt. Eine
Umarmung wird repräsentiert durch 2 Menschen die man aus den 10 auswählt,
deswegen "2 aus 10".
Ein einfacheres Beispiel zur Verdeutlichung: Wenn wir uns nur 3 Personen (A,B
und C) anschauen und nach der Anzahl der Umarmungen fragen, dann gibt es
folgende Möglichkeiten:
A+B
B+C
A+C
Damit sind dann alle möglichen abgedeckt. Das ist genau "2 aus 3". Wenn jetzt
noch die Reihenfolge eine Rolle spielen würde, was es aber nicht tut, dann gäbe
es folgende Möglichkeiten:
A+B
B+A
B+C
C+B
A+C
C+A
was dann mit Formel mn ∗ m! = 32 ∗ 2! = 3 ∗ 2! = 6
Mit 10 Leuten kann man sich das auch nochmal aufschreiben, auch wenn es dann
etwas „aufwendiger“ wird.
1
Ich habe eine Frage bezüglich der Dichtefunktion und Verteilungsfunktion von
stetigen Zusfallsvariablen.
Im Übungsblatt 3 , Aufgabe 2, haben wir eine Verteilungsfunktion gegeben und
mussten diese „nur“ ableiten um von gegeben F(x) auf f(x) die Dichtefunktion zu
kommen.
Wäre die Aufgabe andersrum gestellt, müsste man also von der Dichtefunktion
f(x) auf die Verteilungsfunktion F(x) kommen, würde man doch einfach integrieren. Man würde die Stammfunktion bilden, richtig ?
FRAGE: Hier setzte ich aber noch keine Intervallsgrenzen ein, weil dann habe ich
ja keine Verteilungsfunktion mehr in Abhängigkeit von x sondern schon konkrete
Wahrscheinlichkeiten ausgerechnet wenn ich die Grenzen (2 und 4) einsetzte beim
Integrieren. Ich muss also die Stammfunktion von f(x) bilden um auf F(x) zu
kommen, aber ohne die Intervallsgrenzen (hier 2 und 4 ) einzusetzen ?
FRAGE: Warum setzten wir dann bei Aufgabenblatt 5, Aufgabe 1 schon die Intervallsgrenzen ein wenn wir versuchen von f(x) auf F(x) zu kommen ? (wenn
nämlich die Intervallsgrenzen nicht eingesetzt und Ober - Untergrenze abgezogen
werden, dann kommt man zum falschen Ergebnis, nur die Stammfunktion bilden
wie bei Blatt 3, Aufgabe 2 funktioniert hier nicht und ich frage mich warum ?
Zudem haben wir in den Übungen nie Wahrscheinlichkeiten von den Intervallen
ausgerechnet, wie relevant ist es dann?
Antwort:
Nach 12.16 ist die Verteilungsfunktion folgendermaßen definiert:
Z x
F(x) =
f (t)dt
−∞
Für die Dichtefunktion von Augabe 3.2 gilt also:
!
1
F(x) =
− t + 2 dt
2
−∞
!
Z x
1
=
− t + 2 dt
2
2
"
#x
12
= − t + 2t
4
2
!
!
1 2
1 2
= − x + 2x − − 2 + 2 · 2
4
4
1
= − x2 + 2x − (−1 + 4)
4
1 2
= − x + 2x − 3 für 2 ≤ x ≤ 4
4
Z
x
1
Die erste Umformung kann man hier machen, da die Dichte zwischen −∞ und 2
ja immer 0 ist, also gilt:
!
Z 2
Z 2
1
F(2) =
− t + 2 dt =
0dt = 0
2
−∞
−∞
.
Für die Dichtefunktion von Aufgabe 5.1 ergibt sich:
Z x
F(x) =
λe−λt dt
Z−∞
x
=
λe−λt dt
0
= 1 − e−λx
für
x≥0
Wahrscheinlichkeiten für Intervalle auszurechnen, ist relevant. Vergleiche hierzu
das ergänzende Beispiel zur Exponentialverteilung.
2
Übungsblatt 3 Aufgabe 1f)
• Wäre es möglich die Formel der empirischen Varianz mit in die Fomelsammlung aufzunehmen?
• Was mache ich beim Umformen/Formel aufstellen falsch:
1
· (0 − 1,12 + 48 − 1,12 + 124 − 1,12 )
99
Antwort:
Die Formel der empirischen Varianz findet man in der Formelsammlung zur Vorlesung Statistik I, auf Seite 3. Diese lautet:
n
s2 =
n
1X
1X 2
(xi − x̄)2 =
x − x̄2
n i=1
n i=1 i
In der Übung wurde die empirische Varianz wie folgt berechnet:
n
s2 =
1X 2
x − x̄2
n i=1 i
1 2
(0 + . . . + 02 + 12 + . . . + 12 + 22 + . . . + 22 ) − 1,12
100
1
(21 · 02 + 48 · 12 + 31 · 22 ) − 1,12 = 1,72 − 1,21 = 0,51
=
100
=
Eine andere Möglichkeit wäre:
n
1X
(xi − x̄)2
n i=1
i
1 h
=
(0 − 1,1)2 + . . . + (1 − 1,1)2 + . . . + . . . + (2 − 1,1)2
100
i
1 h
=
21 · (0 − 1,1)2 + 48 · (1 − 1,1)2 + 31 · (2 − 1,1)2 = 0,51
100
s2 =
1
Ich hätte eine Frage zu. Blatt 5 2c). Wieso fällt hier plötzlich das Lamda der
Exponentialfunktion weg im Vergleich zu den vorherigen Teilaufgaben?
Noch eine allgemeine Frage: Sollte man an einer Verteilungsfunktion erkennen
können um welche Verteilung es sich handelt?
Antwort:
Die Verteilungsfunktion der Exponentialverteilung lautet:
(
1 − exp(−λx) x ≥ 0
F(x) =
0
x<0
In Teilaufgabe c) fällt λ nicht weg. Mit λ = 6 und x = 0,5 ergibt sich:
P(X > 0,5) = 1−P(X ≤ 0,5) = 1−F(0,5) = 1−[1−exp((−6)·0,5)] = exp(−3) = 0,0498
Eine Zufallsvariable wird durch deren Verteilungsfunktion eindeutig und vollständig beschrieben (Vgl. Folie 12.12). Man kann also an der Verteilungsfuntion einer
Zufallsvariablen erkennen, um welchen Verteilungstyp es sich handelt.
1
Ich komme mit dem Lösungsweg bei der Aufgabe 4 des Übungsblattes 3 einfach nicht zurecht.
Warum ist das Intervall 10 ≤ x ≤ 20 äquivalent zu |x − 15| ≤ 5?
Kann man immer davon ausgehen, dass es ein symmetrisches Intervall ist und E(x) immer
in der Mitte liegt?
Antwort:
10 ≤ x ≤ 20
⇔ − 5 ≤ x − 15 ≤ 5
⇔ x − 15 ≥ −5 und x − 15 ≤ 5
⇔|x − 15| ≤ 5
(Definition Betrag)
Die Ungleichung von Tschebyschew gibt eine Untergrenze an, für die Wahrscheinlichkeit, dass
die Realisierung einer Zufallsvariable in ein Intervall fällt, welches symmetrisch um den Erwartungswert liegt.
Die Ungleichung von Tschebyschew ist damit auch anwendbar, wenn das gegebene Intervall
zwar selbst nicht symmetrisch um den Erwartungswert liegt, aber ein Intervall enthält, das symmetrisch um den Erwartungswert liegt. Hat man beispielsweise eine Zufallsvariable mit Varianz
4 und Erwartungswert 16 gegeben und sucht hier nach der Untergrenze für die Wahrscheinlichkeit, dass eine Realisierung der Zufallsvariable im Intervall [10;20] liegt, so kann man zur
Abschätzung das Intervall [12;20] heranziehen, welches im Intervall [10;20] enthalten ist und
symmetrisch um den Erwartungswert 16 liegt. Damit folgt folgende Abschätzung mithilfe von
Tschebyschews-Ungleichung:
P (10 ≤ X ≤ 20) ≥ P (12 ≤ X ≤ 20) = P (|X − 16| ≤ 4)
Tschebyschew
≥
=1−
1−
Var (X)
c2
4
3
= = 0,75
16
4
Ich habe eine Frage zu Blatt 5, Aufgabe 4a).
Und zwar ist dort die Wahrscheinlichkeit gesucht, dass der Erwartungswert von 50 mm um mehr
als 3 mm unterschritten wird. Gesucht ist also P (X < 47mm).
Ich habe P (X ≤ 46mm) berechnet. Warum wird er in der Lösung P (X ≤ 47mm) berechnet,
obwohl es heißt ”kleiner 47 mm”?
Antwort:
Beachte, dass es sich in der Aufgabe um eine stetige Zufallsvariable handelt (Normalverteilung).
Die Wahrscheinlichkeit, dass es eine stetige Zufallsvariable einen konkreten Wert annimmt ist
immer 0:
Z
47
P (X = 47) = P (47 ≤ X ≤ 47) =
f (x)dx = 0
47
Daraus folgt direkt, dass
P (X < 47) = P (X ≤ 47).
Im Fall einer stetigen Zufallsvariablen gilt auf jeden Fall, dass
P (X < 47) 6= P (X ≤ 46).
Denn
und
P (X < 47) = P (46 < X < 47) + P (X ≤ 46)
s.o.
P (46 < X < 47) = P (46 ≤ X ≤ 47) =
Z
47
f (x)dx > 0.
46
Anders ist das bei einer diskreten Zufallsvariable. Z.B. gibt eine Poisson-verteilte Zufallsvariable
Y an, wie oft ein Ereignis in einer gewissen Zeitspanne passiert. Sie zählt also (in diskreten
Werten) die Anzahl der Vorkommnisse. Hier gilt dann beispielsweise:
X
X
P (Y < 4) =
f (Y ) =
f (Y ) = P (Y ≤ 3)
Y <4
Y ≤3