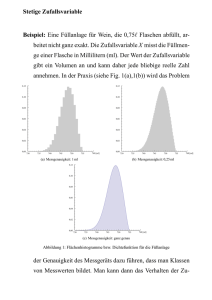
Document

2. Zufallsvariable, Verteilungsfunktion, Erwartungswert, momentenerzeugende Funktion
Ziel des Kapitels:
• Mathematische Präzisierung der Konzepte
Zufallsvariable
Verteilungsfunktion
Dichtefunktion
Erwartungswerte und Momente
Momentenerzeugende Funktion
8
Dazu zunächst:
• Wiederholung der Begriffe
Zufallsvorgang
Ergebnis und Ergebnismenge
Ereignis
Wahrscheinlichkeit
(vgl. Wilfling (2011), Kapitel 2)
9
2.1 Grundlegende Begriffe
Definition 2.1: (Zufallsvorgang, Zufallsexperiment)
Unter einem Zufallsvorgang verstehen wir einen Vorgang, bei
dem
(a) im Voraus feststeht, welche möglichen Ausgänge dieser theoretisch haben kann,
(b) der sich einstellende, tatsächliche Ausgang im Voraus jedoch
unbekannt ist.
Zufallsvorgänge, die geplant sind und kontrolliert ablaufen, heißen
Zufallsexperimente.
10
Beispiele für Zufallsexperimente:
• Ziehung der Lottozahlen
• Roulette, Münzwurf, Würfelwurf
• ’Technische Versuche’
(Härtetest von Stahlproben etc.)
In der VWL:
• Oft keine Zufallsexperimente
(historische Daten, Bedingungen nicht kontrollierbar)
• Moderne VWL-Disziplin: Experimentelle Ökonomik
11
Definition 2.2: (Ergebnis, Ergebnismenge)
Die Menge aller möglichen Ausgänge eines Zufallsvorgangs heißt
Ergebnismenge und wird mit Ω bezeichnet. Ein einzelnes Element ω ∈ Ω heißt Ergebnis.
Beispiele:
• Zufallsvorgang ’Werfen eines Würfels’:
Ω = {1, 2, 3, 4, 5, 6}
• Zufallsvorgang ’Werfen einer Münze solange, bis Kopf erscheint’:
Ω = {K, ZK, ZZK, ZZZK, ZZZZK, . . .}
• Zufallsvorgang ’Bestimmung des morgigen Wechselkurses
zwischen Euro und US-$’:
Ω = [0, ∞)
12
Offensichtlich:
• Die Anzahl der Elemente von Ω kann endlich, abzählbar unendlich oder nicht abzählbar unendlich sein
Jetzt:
• Mengentheoretische Definition des Begriffes ’Ereignis’
Definition 2.3: (Ereignis)
Unter einem Ereignis verstehen wir
Ergebnissen eines Zufallsvorgangs,
Teilmenge der Ergebnismenge Ω.
tritt ein’, wenn der Zufallsvorgang
eine Zusammenfassung von
d.h.
ein Ereignis ist eine
Man sagt ’Das Ereignis A
ein ω ∈ A als Ergebnis hat.
13
Bemerkungen:
• Notation von Ereignissen: A, B, C, . . . oder A1, A2, . . .
• A = Ω heißt das sichere Ereignis
(denn für jedes Ergebnis ω gilt: ω ∈ A)
• A = ∅ (leere Menge) heißt das unmögliche Ereignis
(denn für jedes ω gilt: ω ∈
/ A)
• Falls das Ereignis A eine Teilmenge des Ereignisses B ist
(A ⊂ B), so sagt man: ’Das Eintreten von A impliziert das
Eintreten von B’
(denn für jedes ω ∈ A folgt ω ∈ B)
Offensichtlich:
• Ereignisse sind Mengen
−→ Anwendung von Mengenoperationen auf Ereignisse
14
Ereignisverknüpfungen (Mengenoperationen):
• Durchschnittsereignis (-menge):
n
T
i=1
Ai tritt ein, wenn alle Ai eintreten
• Vereinigungsereignis (-menge):
n
S
i=1
Ai tritt ein, wenn mindestens ein Ai eintritt
• Differenzereignis (-menge):
C = A\B tritt ein, wenn A eintritt, aber B nicht
• Komplementärereignis:
C = Ω\A ≡ A tritt ein, wenn A nicht eintritt
• Die Ereignisse A und B heißen unvereinbar oder disjunkt,
wenn A ∩ B = ∅
(beide Ereignisse können nicht gleichzeitig eintreten)
15
Jetzt:
• Jedem Ereignis A soll eine Zahl P (A) zugeordnet werden,
welche die Wahrscheinlichkeit für das Eintreten von A repräsentiert
• Formal:
P : A −→ P (A)
Frage:
• Welche Eigenschaften sollte die Zuordnung (Mengenfunktion) P besitzen?
16
Definition 2.4: (Kolmogorov’sche Axiome)
Die folgenden 3 Mindestanforderungen an P werden als Kolmogorov’sche Axiome bezeichnet:
• Nichtnegativität: Für alle A soll gelten: P (A) ≥ 0
• Normierung: P (Ω) = 1
• Additivität: Für zwei disjunkte Ereignisse A und B (d.h. für
A ∩ B = ∅) soll gelten:
P (A ∪ B) = P (A) + P (B)
17
Es ist leicht zu zeigen:
• Die 3 Kolmogorov’schen Axiome implizieren bestimmte Eigenschaften und Rechenregeln für Wahrscheinlichkeiten
Satz 2.5: (Eigenschaften von Wahrscheinlichkeiten)
Aus den Kolmogorov’schen Axiomen ergeben sich folgende Eigenschaften für die Wahrscheinlichkeit beliebiger Ereignisse:
• Wahrscheinlichkeit des Komplimentärereignisses:
P (A) = 1 − P (A)
• Wahrscheinlichkeit des unmöglichen Ereignisses:
P (∅) = 0
• Wertebereich der Wahrscheinlichkeit:
0 ≤ P (A) ≤ 1
18
Weiterhin:
• Allgemeine Rechenregeln für Wahrscheinlichkeiten, die aus
den Kolmogorov’schen Axiomen folgen
Satz 2.6: (Rechenregeln für Wahrscheinlichkeiten)
Aus den Kolmogorov’schen Axiomen ergeben sich die folgenden
Rechenregeln für die Wahrscheinlichkeit von beliebigen Ereignissen A, B, C:
• Additionssatz für Wahrscheinlichkeiten:
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
(Wahrscheinlichkeit, dass A oder B eintritt)
19
• Additionssatz für 3 Ereignisse:
P (A ∪ B ∪ C) = P (A) + P (B) + P (C)
−P (A ∩ B) − P (B ∩ C)
−P (A ∩ C) + P (A ∩ B ∩ C)
(Wahrscheinlichkeit, dass A oder B oder C eintritt)
• Wahrscheinlichkeit des Differenzereignisses:
P (A\B) = P (A ∩ B)
= P (A) − P (A ∩ B)
20
Man beachte:
• Wenn das Ereignis B das Ereignis A impliziert (d.h.
wenn B ⊂ A gilt), dann folgt
P (A\B) = P (A) − P (B)
21
2.2 Zufallsvariable, Verteilungs- und Dichtefkt
Häufige Situation in der Praxis:
• Es interessiert weniger das konkrete Ergebnis ω ∈ Ω eines
Zufallsexperimentes, sondern eine Zahl, die von ω abhängt
Beispiele:
• Gewinn in Euro im Roulette
• Gewinn einer Aktie an der Börse
• Monatsgehalt einer zufällig ausgewählten Person
Intuitive Bedeutung einer Zufallsvariablen:
• Vorschrift, die das ’abstrakte’ ω in eine Zahl übersetzt
22
Definition 2.7: (Zufallsvariable [kurz: ZV])
Unter einer Zufallsvariablen versteht man formal eine (mathematische) Funktion
X : Ω −→ R
ω −→ X(ω).
Bemerkungen:
• Eine Zufallsvariable ordnet jedem Ergebnis ω ∈ Ω eine reelle
Zahl zu
• Intuition:
Eine Zufallsvariable X charakterisiert eine Zahl, deren Wert
man noch nicht kennt
23
• Nach der Durchführung des Zufallsexperimentes realisiert sich
die Zufallsvariable X im Wert x
• x heißt die Realisation oder Realisierung der ZV X nach
Durchführung des zugehörigen Zufallsexperimentes
• In dieser VL:
Zufallsvariablen werden immer mit Großbuchstaben, Realisationen immer mit Kleinbuchstaben bezeichnet
• Die Zufallsvariable X beschreibt die Situation ex ante, d.h. vor
der tatsächlichen Durchführung des Zufallsexperimentes
• Die Realisation x beschreibt die Situation ex post, d.h. nach
der Durchführung des Zufallsexperimentes
24
Beispiel 1:
• Betrachte den 1-maligen Münzwurf (Z=Zahl, K=Kopf). Die
ZV X bezeichne die ’Anzahl der Köpfe’ bei diesem Zufallsexperiment
• Es gilt:
Ω = {K, Z}
Die ZV X kann 2 Werte annehmen:
X(Z) = 0,
X(K) = 1
25
Beispiel 2:
• Betrachte den 3-maligen Münzwurf. Die ZV X bezeichne
erneut die ’Anzahl der Köpfe’
• Es gilt:
Ω = {(K,
K,
K)}, (K,
K,
Z)}, . . . , (Z,
Z,
Z)}}
|
{z
|
{z
|
{z
=ω1
=ω2
=ω8
Die Zufallsvariable X ist definiert durch
X(ω) = Anzahl der K in ω
• Offensichtlich:
X ordnet verschiedenen ω dieselbe Zahl zu, z.B.
X((K, K, Z)) = X((K, Z, K)) = X((Z, K, K)) = 2
26
Beispiel 3:
• Aus einer Personengruppe wird zufällig 1 Person ausgewählt.
Die ZV X soll den Erwerbsstatus der ausgewählten Person
bezeichnen
• Es gilt:
Ω = {’erwerbstätig’
{z
}, |’nicht erwerbstätig’
{z
}}
|
=ω1
=ω2
• Die ZV X kann codiert werden durch
X(ω1) = 1,
X(ω2) = 0
27
Beispiel 4:
• Das Zufallsexperiment bestehe in der Messung des morgigen
Kurses einer bestimmten Aktie. Die ZV X bezeichne diesen
Aktienkurs
• Es gilt Ω = [0, ∞), d.h. X ist definiert durch
X(ω) = ω
Zwischenfazit:
• Die ZV X kann verschiedene Werte annehmen und zwar mit
bestimmten Wskt’en
28
Frage:
• Wie kann man diese Wskt’en bestimmen und mit diesen rechnen?
Zunächst vereinfachte Schreibweise: (a, b, x ∈ R)
• P (X = a) ≡ P ({ω|X(ω) = a})
• P (a < X < b) ≡ P ({ω|a < X(ω) < b})
• P (X ≤ x) ≡ P ({ω|X(ω) ≤ x})
Lösung:
• Die Berechnung solcher Wskt’en kann über die sogenannte
Verteilungsfunktion der ZV’en X erfolgen
29
Intuition:
• Die Verteilungsfunktion der ZV’en X charakterisiert die Wahrscheinlichkeiten, mit denen sich die potenziellen Realisationen x auf der reellen Zahlenachse verteilen
(die sogenannte Verteilung der ZV’en X)
Definition 2.8: (Verteilungsfunktion [kurz: VF])
Gegeben sei die Zufallsvariable X. Unter der Verteilungsfunktion der ZV’en X (in Zeichen: FX ) versteht man die folgende
Abbildung:
FX : R −→ [0, 1]
x −→ FX (x) = P ({ω|X(ω) ≤ x}) = P (X ≤ x).
30
Beispiel:
• Betrachte den 3-fachen Münzwurf.
’Anzahl Kopf’.
Die ZV X messe die
• Zunächst gilt:
Ω = {(K,
K,
K)}, (K,
K,
Z)}, . . . , (Z,
Z,
Z)}}
|
|
|
{z
{z
{z
= ω1
= ω2
= ω8
• Für die Wskt’en der ZV X errechnet sich:
P (X = 0) = P ({(Z, Z, Z)}) = 1/8
P (X = 1) = P ({(Z, Z, K), (Z, K, Z), (K, Z, Z)}) = 3/8
P (X = 2) = P ({(Z, K, K), (K, Z, K), (K, K, Z)}) = 3/8
P (X = 3) = P ({(K, K, K)}) = 1/8
31
• Daraus ergibt sich die VF:
FX (x) =



 0.000

 0.125


0.5

 0.875





1
für x < 0
für 0 ≤ x < 1
für 1 ≤ x < 2
für 2 ≤ x < 3
für x ≥ 3
Bemerkungen:
• Es genügt (fast immer), lediglich die VF FX der ZV X zu
kennen
• Oft ist es in praxi gar nicht möglich, den Grundraum Ω oder
die explizite Abbildung X : Ω −→ R anzugeben
(jedoch kann man meistens die VF FX aus sachlogischen
Überlegungen heraus angeben)
32
Allgemeingültige Eigenschaften von FX :
• FX (x) ist monoton wachsend
• Es gilt stets:
lim FX (x) = 0
x→−∞
und
lim FX (x) = 1
x→+∞
• FX ist rechtsseitig stetig, d.h.
lim
F (z) = FX (x)
z→x X
z>x
33
Fazit:
• VF FX (x) der ZV’en X gibt Antwort auf die Frage
’Wie hoch ist die Wahrscheinlichkeit, dass X höchstens den
Wert x annimmt?’
Jetzt:
• Antwort auf die Frage
’Welchen Wert wird die ZV’e X mit einer vorgegebenen
Wahrscheinlichkeit p ∈ (0, 1) nicht überschreiten?’
−→ Quantilfunktion der ZV’en X
34
Definition 2.9: (Quantilfunktion)
Gegeben sei die ZV X mit VF FX . Für jeden reellen Wert p ∈
(0, 1) versteht man unter der Quantilfunktion von X (in Zeichen:
QX (p)) die folgende Abbildung:
QX : (0, 1) −→ R
p
−→ QX (p) = min{x|FX (x) ≥ p}.
Der Wert der Quantilfunktion xp = QX (p) heißt p − Quantil der
ZV’en X.
Bemerkungen:
• Das p-Quantil xp ist die kleinste Zahl x ∈ R mit der Eigenschaft, dass FX (x) den Wert p erreicht oder überschreitet
• Interpretiert man p ∈ (0, 1) als eine Wahrscheinlichkeit, so ist
das p-Quantil xp die kleinste Realisation der ZV’en X, die X
mit Wskt. p nicht überschreitet
35
Spezielle Quantile:
• Median: p = 0.5
• Quartile: p = 0.25, 0.5, 0.75
• Quintile: p = 0.2, 0.4, 0.6, 0.8
• Dezile: p = 0.1, 0.2, . . . , 0.9
Jetzt:
• Typisierung von ZV’en
(diskrete vs. stetige ZV’en)
36
Grund:
• Unterschiedliche mathematische Methoden zur Behandlung
von ZV’en
Bei diskreten ZV’en:
• Endliche und unendliche Summen
Bei stetigen ZV’en:
• Differential- und Integralrechnung
Bemerkungen:
• Es gibt auch ZV’en, die gleichzeitig teilweise diskret und teilweise stetig sind
• Solche ZV’en werden hier nicht behandelt
37
Definition 2.10: (Diskrete Zufallsvariable)
Die ZV X heißt diskret, wenn sie entweder
(a) nur endlich viele Realisationen x1, x2, . . . , xJ oder
(b) abzählbar unendlich viele Realisationen x1, x2, . . .
mit streng positiver Wahrscheinlichkeit annehmen kann, d.h. falls
für alle j = 1, . . . , J, . . . gilt
P (X = xj ) > 0
und
J,...
X
P (X = xj ) = 1.
j=1
38
Typische diskrete Merkmale sind:
• Zählmerkmale (’X = Anzahl von . . .’)
• Codierte qualitative Merkmale
Weitere Definitionen:
Definition 2.11: (Träger einer diskreten Zufallsvariablen)
Die Menge aller Realisationen, die eine diskrete ZV X mit streng
positiver Wskt. annehmen kann, heißt Träger von X (in Zeichen:
TX ):
TX = {x1, . . . , xJ }
bzw.
TX = {x1, x2, . . .}.
39
Definition 2.12: (Wahrscheinlichkeitsfunktion)
Für eine diskrete ZV X heißt die Funktion
fX (x) = P (X = x)
die Wahrscheinlichkeitsfunktion von X.
Bemerkungen:
• Die Wahrscheinlichkeitsfunktion fX der ZV X nimmt nur für
die Elemente des Trägers TX positive Werte an. Für Werte
außerhalb des Trägers, d.h. für x ∈
/ TX , gilt fX (x) = 0:
fX (x) =
(
P (X = xj ) > 0
0
für x = xj ∈ TX
für x ∈
/ TX
40
• Die Wahrscheinlichkeitsfkt. fX hat die Eigenschaften
fX (x) ≥ 0 für alle x
X
fX (xj ) = 1
xj ∈TX
• Für eine beliebige Menge A ⊂ R berechnet sich die Wskt. des
Ereignisses {ω|X(ω) ∈ A} = {X ∈ A} durch
P (X ∈ A) =
X
fX (xj )
xj ∈A
41
Beispiel:
• Betrachte 3-fachen Münzwurf und X = ’Anzahl Kopf’
(vgl. Folien 31, 32)
• Offensichtlich: X ist diskret mit dem Träger
TX = {0, 1, 2, 3}
• Die Wahrscheinlichkeitsfunktion ist gegeben durch
fX (x) =

 P (X = 0) = 0.125





 P (X = 1) = 0.375
P (X = 2) = 0.375

 P (X = 3) = 0.125





0
für x = 0
für x = 1
für x = 2
für x = 3
für x ∈
/ TX
42
• Die Verteilungsfunktion ist gegeben durch
FX (x) =


0.000





 0.125
0.5



 0.875



1
für x < 0
für 0 ≤ x < 1
für 1 ≤ x < 2
für 2 ≤ x < 3
für x ≥ 3
Offensichtlich:
• Für die Verteilungsfunktion gilt
FX (x) = P (X ≤ x) =
X
{xj ∈TX |xj ≤x}
=P (X=xj )
z }| {
fX (xj )
43
Fazit:
• Die VF einer diskreten ZV’en X ist eine Treppenfunktion
mit Sprüngen an den Stellen xj ∈ TX . Die Sprunghöhe an
der Stelle xj beträgt
FX (xj ) − x→x
lim F (x) = P (X = xj ) = fX (xj ),
j
x<xj
d.h. die Sprunghöhe ist der Wert der Wskt.-Funktion
(Beziehung: Verteilungs- und Wahrscheinlichkeitsfunktion)
44
Jetzt:
• Definition von stetigen Zufallsvariablen
Intuition:
• Im Gegensatz zu diskreten ZV’en können stetige ZV’e überabzählbar viele Realisationen (z.B. jede reelle Zahl in einem
Intervall) annehmen
Tatsächlich:
• Definition stetiger ZV’en komplizierter (technischer)
45
Definition 2.13: (Stetige ZV, Dichtefunktion)
Eine ZV X heißt stetig, wenn sich ihre Verteilungsfunktion FX
als Integral einer Funktion fX : R −→ [0, ∞) schreiben lässt,
d.h. wenn
FX (x) =
Z x
−∞
fX (t)dt
für alle x ∈ R.
Die Funktion fX (x) heißt Dichtefunktion [kurz: Dichte] von X.
Bemerkungen:
• Die VF FX einer stetigen ZV’en X ist (eine) Stammfunktion
der Dichtefunktion fX
• FX (x) = P (X ≤ x) ist gleich dem Flächeninhalt unter der
Dichtefunktion fX von −∞ bis zur Stelle x
46
Verteilungsfunktion FX und Dichte fX
fX(t)
P(X ≤ x) = FX(x)
x
t
47
Eigenschaften der Dichtefunktion fX :
1. Die Dichte fX ist niemals negativ, d.h.
fX (x) ≥ 0
für alle x ∈ R
2. Die Fläche unter der Dichte ist gleich 1, d.h.
Z +∞
−∞
fX (x)dx = 1
3. Wenn FX (x) differenzierbar ist, gilt
0 (x) ≡ dF (x)/dx
fX (x) = FX
X
48
Beispiel: (Gleichverteilung über [0, 10])
• Gegeben sei die ZV X mit Dichtefunktion
fX (x) =
(
0
0.1
, für x ∈
/ [0, 10]
, für x ∈ [0, 10]
• Berechnung der VF FX :
Für x < 0 gilt:
FX (x) =
Z x
−∞
fX (t) dt =
Z x
−∞
0 dt = 0
49
Für x ∈ [0, 10] gilt:
FX (x) =
Z x
=
Z 0
−∞
fX (t) dt
0 dt +
| −∞
{z
=0
}
Z x
0
0.1 dt
= [0.1 · t]x0
= 0.1 · x − 0.1 · 0
= 0.1 · x
50
Für x > 10 gilt:
FX (x) =
Z x
=
Z 0
−∞
fX (t) dt
0 dt +
{z
| −∞
=0
= 1
}
Z 10
|0
0.1 dt +
{z
=1
}
Z ∞
0 dt
| 10{z }
=0
51
Jetzt:
• Wskt.’en für Intervalle, d.h. (für a, b ∈ R, a < b)
P (X ∈ (a, b]) = P (a < X ≤ b)
• Es gilt:
P (a < X ≤ b) = P ({ω|a < X(ω) ≤ b})
= P ({ω|X(ω) > a} ∩ {ω|X(ω) ≤ b})
= 1 − P ({ω|X(ω) > a} ∩ {ω|X(ω) ≤ b})
= 1 − P ({ω|X(ω) > a} ∪ {ω|X(ω) ≤ b})
= 1 − P ({ω|X(ω) ≤ a} ∪ {ω|X(ω) > b})
52
= 1 − [P (X ≤ a) + P (X > b)]
= 1 − [FX (a) + (1 − P (X ≤ b))]
= 1 − [FX (a) + 1 − FX (b)]
= FX (b) − FX (a)
=
Z b
=
Z b
−∞
a
fX (t) dt −
Z a
−∞
fX (t) dt
fX (t) dt
53
Intervall-Wahrscheinlichkeit mit den Grenzen a und b
fX(x)
P(a < X ≤ b)
a
b
x
54
Wichtiges Ergebnis für stetige ZV X:
P (X = a) = 0
für alle a ∈ R
Begründung:
P (X = a) = lim P (a < X ≤ b) = lim
b→a
=
Z a
a
Z b
b→a a
fX (x) dx
fX (x)dx = 0
Fazit:
• Die Wskt., dass eine stetige ZV X einen einzelnen Wert annimmt, ist immer Null!!
55
Punkt-Wahrscheinlichkeit
fX(x)
a
b3
b2
b1
x
56
Vorsicht:
• Das bedeutet nicht, dass dieses Ereignis unmöglich ist
Konsequenz:
• Da bei stetigen ZV’en für alle a ∈ R stets P (X = a) = 0 gilt,
folgt für stetige ZV stets
P (a < X < b) = P (a ≤ X < b) = P (a ≤ X ≤ b)
= P (a < X ≤ b) = FX (b) − FX (a)
(Ob Intervalle offen oder geschlossen sind, spielt für die
Wskt.-Bestimmung bei stetigen ZV keine Rolle)
57
2.3 Erwartungswerte, Momente und momentenerzeugende Funktionen
Bekannt aus WRUSS:
• Der Erwartungswert einer ZV’en X ist eine Maßzahl für die
Lage der Verteilung (Lagemaß)
Definition 2.14: (Erwartungswert)
Der Erwartungswert der ZV’en X [in Zeichen: E(X)] ist definiert
als
E(X) =

X

xj · P (X = xj )




 {xj ∈TX }






Z +∞
−∞
x · fX (x) dx
, falls X diskret ist
.
, falls X stetig ist
58
Bemerkungen:
• Der Erwartungswert der ZV’en X entspricht also (in etwa)
der Summe aller möglichen Realisationen jeweils gewichtet
mit der Wskt. ihres Eintretens
• Anstelle von E(X) schreibt man häufig µX
• Es gibt ZV’en, die keinen Erwartungswert besitzen
(vgl. Übung)
59
Beispiel 1: (Diskrete ZV)
• Man betrachte den 2-maligen Würfelwurf. Die ZV X stehe
für die (betragliche) Differenz der Augenzahlen. Man berechne den Erwartungswert von X
• Zunächst ergibt sich als Träger der Zufallsvariablen
TX = {0, 1, 2, 3, 4, 5}
60
• Die Wahrscheinlichkeitsfunktion ist gegeben durch
fX (x) =


 P (X = 0) = 6/36



P (X = 1) = 10/36



 P (X = 2) = 8/36


P (X = 3) = 6/36


 P (X = 4) = 4/36





P (X = 5) = 2/36



0
für x = 0
für x = 1
für x = 2
für x = 3
für x = 4
für x = 5
/ TX
für x ∈
• Als Erwartungswert ergibt sich
6
10
8
6
4
2
E(X) = 0 ·
+1·
+2·
+3·
+4·
+5·
36
36
36
36
36
36
=
70
= 1.9444
36
61
Beispiel 2: (Stetige ZV)
• Es sei X eine stetige ZV mit der Dichte

 x
, für 1 ≤ x ≤ 3
fX (x) =
4
 0
, sonst
• Zur Berechnung des Erwartungswertes spaltet man das Integral auf:
E(X) =
=
Z +∞
−∞
Z 1
x · fX (x) dx
Z 3
Z
+∞
x
0 dx +
0 dx
x · dx +
4
−∞
3
1
62
=
•
”
1 1 3 3
dx =
·
·x
4 3
1 4
1
Z 3 2
x
’
1
27 1
=
·
−
4
3
3
“
26
= 2.1667
=
12
Häufige Situation:
• Kenne ZV X mit Wskt.- oder Dichtefunktion fX
• Suche den Erwartungswert der transformierten ZV
Y = g(X)
63
Satz 2.15: (Erwartungswert einer Transformierten)
Gegeben sei die ZV X mit Wskt.- oder Dichtefunktion fX . Für
eine beliebige (Baire)Funktion g : R −→ R berechnet sich der
Erwartungswert der transformierten ZV Y = g(X) als
E(Y ) = E[g(X)]
=

X

g(xj ) · P (X = xj )




 {xj ∈TX }






Z +∞
−∞
g(x) · fX (x) dx
, falls X diskret ist
.
, falls X stetig ist
64
Bemerkungen:
• Alle Funktionen, die in unserer Veranstaltung auftauchen,
sind Baire-Funktionen
• Für den Spezialfall g(x) = x (die Identitätsfunktion) fällt der
Satz 2.15 mit der Definition 2.14 zusammen
Zunächst:
• Erste wichtige Rechenregeln für Erwartungswerte
65
Satz 2.16: (Regeln für E-Werte)
Es seien X eine beliebige ZV (diskret oder stetig), c, c1, c2 ∈ R
konstante Zahlen und g, g1, g2 : R −→ R Funktionen. Dann gelten
die folgenden Aussagen:
1. E(c) = c.
2. E[c · g(X)] = c · E[g(X)].
3. E[c1 · g1(X) + c2 · g2(X)] = c1 · E[g1(X)] + c2 · E[g2(X)].
4. Falls g1(x) ≤ g2(x) für alle x ∈ R gilt, so folgt:
E[g1(X)] ≤ E[g2(X)].
Beweis: Übungsaufgabe
66
Jetzt:
• Betrachte die ZV X (diskret oder stetig) und die explizite
Funktion g(x) = [x − E(X)]2
−→ Varianz und Standardabweichung der ZV’en X
Definition 2.17: (Varianz, Standardabweichung)
Für eine beliebige stetige oder diskrete ZV X ist die Varianz
von X [in Zeichen: Var(X)] definiert als die erwartete quadrierte
Abweichung der ZV von ihrem Erwartungswert E(X), d.h.
Var(X) = E[(X − E(X))2].
Unter der Standardabweichung von X [in Zeichen: SD(X)] versteht man die (positive) Wurzel aus der Varianz, d.h.
q
SD(X) = + Var(X).
67
Bemerkungen:
• Mit g(X) = [X − E(X)]2 und Satz 2.15 (Folie 64) berechnet
sich die Varianz von X explizit als
Var(X) = E[g(X)]
=

X


[xj − E(X)]2 · P (X = xj )



 {xj ∈TX }






Z +∞
−∞
[x − E(X)]2 · fX (x) dx
, für diskretes X
, für stetiges X
• Es gibt ZV’en, die keine endliche Varianz besitzen
(vgl. Übung)
68
Beispiel: (Diskrete ZV)
• Betrachte erneut den 2-maligen Würfelwurf mit der ZV X
als (betraglicher) Differenz der Augenzahlen (vgl. Beispiel 1,
Folie 35). Für die Varianz gilt:
Var(X) = (0 − 70/36)2 · 6/36 + (1 − 70/36)2 · 10/36
+ (2 − 70/36)2 · 8/36 + (3 − 70/36)2 · 6/36
+ (4 − 70/36)2 · 4/36 + (5 − 70/36)2 · 2/36
= 2.05247
Man beachte:
• Die Varianz ist per definitionem ein Erwartungswert
−→ Rechenregeln für Erwartungswerte anwendbar
69
Satz 2.18: (Rechenregeln für Varianzen)
Es seien X eine beliebige ZV (diskret oder stetig) sowie a, b ∈ R
reelle Zahlen. Es gilt
1. Var(X) = E(X 2) − [E(X)]2.
2. Var(a + b · X) = b2 · Var(X).
Beweis: Übungsaufgabe
Jetzt:
• Zwei wichtige Ungleichungen im Zusammenhang mit Erwartungswerten und transformierten ZV’en
70
Satz 2.19: (Allgemeine Chebyshey-Ungleichung)
Es seien X eine beliebige ZV sowie g : R −→ R+ eine nichtnegative Funktion. Dann gilt für jedes k > 0
E [g(X)]
P [g(X) ≥ k] ≤
.
k
Jetzt Spezialfall:
• Betrachte
g(x) = [x − E(X)]2
und
k = r2 · Var(X)
• Hierfür liefert der Satz 2.19
n
2
P [X − E(X)]
≥ r2 · Var(X)
o
(r > 0)
Var(X)
1
≤ 2
= 2
r · Var(X)
r
71
• Nun gilt
n
P [X − E(X)]
2
≥ r2 · Var(X)
o
= P {|X − E(X)| ≥ r · SD(X)}
= 1 − P {|X − E(X)| < r · SD(X)}
• Daraus folgt
1
P {|X − E(X)| < r · SD(X)} ≥ 1 − 2
r
(spezielle Chebyshev-Ungleichung)
72
Bemerkung:
• Die spezielle Chebyshev-Ungleichung gibt die Mindestwahrscheinlichkeit an, mit der eine beliebige ZV in das folgende
(offene oder geschlossene) Intervall fällt:
[E(X) − r · SD(X), E(X) + r · SD(X)]
• Z.B. gilt für r = 3:
8
1
P {|X − E(X)| < 3 · SD(X)} ≥ 1 − 2 =
3
9
was äquivalent ist zu
P {E(X) − 3 · SD(X) < X < E(X) + 3 · SD(X)} ≥ 0.8889
bzw.
P {X ∈ (E(X) − 3 · SD(X), E(X) + 3 · SD(X))} ≥ 0.8889
73
Satz 2.20: (Jensen-Ungleichung)
Es seien X eine beliebige ZV sowie g : R −→ R eine konvexe
(bzw. eine konkave) Funktion, d.h. für alle x gelte g 00(x) ≥ 0
(bzw. g 00(x) ≤ 0). Dann folgt
E [g(X)] ≥ g(E[X]) bzw. E [g(X)] ≤ g(E[X]).
Bemerkung:
• Es ist wichtig zu beachten, dass im Allgemeinen
E [g(X)] 6= g(E[X])
74
Beispiel:
• Betrachte die ZV X und die Funktion g(x) = x2
• Es gilt: g 00(x) = 2 ≥ 0 für alle x, d.h. g ist konvex
• Mit der Jensen-Ungleichung folgt
E
E[X])
[g(X)] ≥ g(
| {z }
| {z }
=E(X 2)
d.h.
=[E(X)]2
E(X 2) − [E(X)]2 ≥ 0
• Mit dem Satz 2.18 folgt also
Var(X) = E(X 2) − [E(X)]2 ≥ 0
(die Varianz einer ZV’en kann niemals negativ sein)
75
Jetzt:
• Betrachte die beliebige ZV X mit E-Wert E(X) = µX , eine
natürliche Zahl n ∈ N sowie die Funktionen
g1(x) = xn
g2(x) = [x − µX ]n
Definition 2.21: (Momente, zentrale Momente)
0 ) ist definiert
(a) Das n-te Moment der ZV’en X (in Zeichen: µn
als
µ0n ≡ E[g1(X)] = E(X n).
(b) Das n-te zentrale Moment um den Erwartungswert (in Zeichen: µn) ist definiert als
µn ≡ E[g2(X)] = E[(X − µX )n].
76
Beziehungen:
• µ01 = E(X) = µX
(das 1. Moment entspricht dem E-Wert)
• µ1 = E[X − µX ] = E(X) − µX = 0
(das 1. zentrale Moment ist immer 0)
• µ2 = E[(X − µX )2] = Var(X)
(das 2. zentrale Moment entspricht der Varianz)
77
Bemerkungen:
• Speziell die ersten 4 Momente einer ZV’en X sind Bausteine
für wichtige Kenngrößen der Verteilung
(Erwartungswert, Varianz, Schiefe, Kurtosis)
• Die Momente einer ZV’en X spielen eine zentrale Rolle in
der theoretischen und angewandten Statistik
• In einigen Fällen kann aus der Kenntnis aller Momente der
ZV’en X die vollständige Verteilung (d.h. die Wahrscheinlichkeits- bzw. die Dichtefunktion) hergeleitet werden
78
Frage:
• Gibt es eine mathematische Funktion, die eine Darstellung
aller Momente einer Verteilung liefert ?
Definition 2.22: (Momentenerzeugende Funktion)
Es sei X eine ZV mit Wskts- bzw. Dichtefunktion fX (x).h Für
i
t·X
eine reelle Zahl t ∈ R betrachte man den Erwartungswert E e
.
Falls dieser E-Wert für alle t aus einem Intervall −h < t < h, h > 0,
existiert, so definiert man die momentenerzeugende Funktion von
X (in Zeichen: mX (t)) als diesen E-Wert, d.h.
mX (t) = E
h
i
t·X
.
e
79
Bemerkungen:
• Die momentenerzeugende Funktion mX (t) wird als Funktion
in t aufgefasst
• Es gibt ZV’en X, für die mX (t) nicht existiert
• Falls mX (t) existiert, so berechnet sich die Funktion aufgrund
des Satzes 2.15 (Folie 64) als
mX (t) = E
=
h
et·X
i

X

et·xj · P (X = xj )




 {xj ∈TX }






Z +∞
−∞
et·x · fX (x) dx
, falls X diskret
, falls X stetig
80
Frage:
• Warum heißt mX (t) momentenerzeugende Funktion ?
Antwort:
• Man betrachte die n-te Ableitung von mX (t) nach t:

X

(xj )n · et·xj · P (X = xj )




 {xj ∈TX }
dn
mX (t) =
n

dt





Z +∞
−∞
xn · et·x · fX (x) dx
, falls X diskret
, falls X stetig
81
• Für die n-te Ableitung an der Stelle t = 0 gilt

X

(xj )n · P (X = xj )



 {x ∈T }

j
X
dn
mX (0) =
n

dt





Z +∞
−∞
xn · fX (x) dx
, falls X diskret
, falls X stetig
= E(X n) = µ0n
(vgl. Definition 2.21(a), Folie 76)
82
Beispiel:
• Es sei X eine stetige ZV mit Dichtefunktion
fX (x) =
(
0
λ · e−λ·x
, falls x < 0
, falls x ≥ 0
(Exponentialverteilung mit Parameter λ > 0)
• Es gilt
h
i
mX (t) = E et·X =
=
für t < λ
Z +∞
0
Z +∞
−∞
et·x · fX (x) dx
λ · e(t−λ)·x dx =
λ
λ−t
83
• Es folgt
m0X (t) =
und somit
λ
(λ − t)2
m0X (0) = E(X) =
1
λ
sowie
sowie
m00X (t) =
2λ
(λ − t)3
2
m00X (0) = E(X 2) = 2
λ
Jetzt:
• Zentrales Resultat über momentenerzeugende Funktionen
84
Satz 2.23: (Identifikationseigenschaft)
Es seien X und Y zwei ZV’en mit Wskts- bzw. Dichtefunktionen fX (·) und fY (·). Angenommen, die beiden momentenerzeugenden Funktionen mX (t) und mY (t) existieren und es gilt
mX (t) = mY (t) für alle t im Intervall −h < t < h, h > 0. Dann
haben die beiden ZV’en identische Verteilungsfunktionen, d.h. es
gilt FX (x) = FY (x) für alle x.
Bemerkung:
• Der Satz 2.23 besagt, dass zu einer gegebenen momentenerzeugenden Funktion mX (t) eine eindeutige Verteilungsfunktion FX (x) gehört
−→ Wenn mX (t) für die ZV X bekannt ist, dann kann man
(zumindest theoretisch) die Verteilung von X bestimmen
• Diese Eigenschaft werden wir in Kapitel 4 benutzen
85
Beispiel:
• Angenommen, die ZV X hat die momentenerzeugende Funktion
1
mX (t) =
für − 1 < t < 1
1−t
• Dann muss die Dichtefunktion von X gegeben sein durch
fX (x) =
(
0
e−x
, falls x < 0
, falls x ≥ 0
(Exponentialverteilung mit Parameter λ = 1)
86
2.4 Spezielle Verteilungen
Bisher:
• Analyse allgemeiner mathematischer Eigenschaften beliebiger
Verteilungen
• Unterscheidung zwischen diskreten und stetigen Verteilungen
• Betrachtung
der Verteilungsfunktion FX (x)
der Wskt- bzw. Dichtefunktion fX (x)
von Erwartungswerten E[g(X)]
der momentenerzeugenden Funktion mX (t)
87
Zentrale Erkenntnis:
• Die Verteilung einer ZV’en X ist (im wesentlichen) durch
fX (x) oder FX (x) bestimmt
• Mit fX (x) lässt sich FX (x) bestimmen
(vgl. Folie 46)
• Aus FX (x) lässt sich (im wesentlichen) fX (x) bestimmen
(vgl. Folie 48)
Frage:
• Wieviele verschiedene Verteilungen gibt es?
88
Antwort:
• Unendlich viele
Jedoch:
• In der Praxis haben sich einige wichtige parametrische Verteilungsfamilien als ’gute’ Modelle für real auftretende Zufallsereignisse herauskristallisiert
• Diese Verteilungsfamilien werden in allen Statistik-Lehrbüchern ausführlich beschrieben
(z.B. in Mosler & Schmid (2008), Mood et al. (1974))
89
• Zentrale diskrete Verteilungsfamilien
Bernoulli-Verteilung
Binomial-Verteilung
Geometrische Verteilung
Poisson-Verteilung
• Zentrale stetige Verteilungsfamilien
Gleichverteilung
Exponentialverteilung
Normalverteilung
90
Bemerkung:
• Die wichtigste parametrische Verteilungsfamilie überhaupt ist
die Normalverteilung
Definition 2.24: (Normalverteilung)
Die stetige ZV X heißt normalverteilt mit Parametern µ ∈ R
und σ 2 > 0 [in Zeichen: X ∼ N (µ, σ 2)], falls X die folgende
Dichtefunktion besitzt:
fX (x) = √

‘
x−µ 2
1
−2 σ
1
·e
2π · σ
,
x ∈ R.
91
Dichtefunktionen der Normalverteilung
fX(x)
N(5,1)
N(0,1)
N(5,3)
N(5,5)
0
5
x
92
Bemerkungen:
• Die Normalverteilung N (0, 1) heißt Standardnormalverteilung.
Ihre Dichte wird oft mit ϕ(x) bezeichnet
• Die Kenntnis aller Eigenschaften sowie das Rechnen mit normalverteilten ZV’en ist zwingende Voraussetzung für diese
Veranstaltung
(vgl. Wilfling (2011), Kapitel 3.4)
93