2.7 Subtraktion

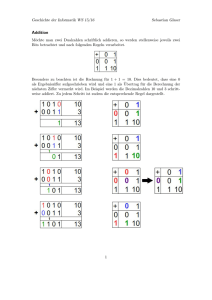
2.7 Subtraktion
2.7.1 Anschaulicher Weg
Zunächst Übung: Drei Aufgaben
(1)
−
(2)
−
(3)
−
Ikonische Darstellung! [Benutzung von Rechtecken!]
Analoges Vorgehen wie in Abschnitt 2.6.1!
2.7.2 Systematische Behandlung
Analoges Vorgehen wie in Abschnitt 2.6.2!
Aber Vorsicht! Reihenfolge der Zahlbereichserweiterungen beachten!
Weg 1:
→ +→ Hier hat man zunächst nur ℚ+, noch nicht
!
m p
m p
Die Subtraktion − ist nur möglich, wenn > ist.
n n
n n
Weg 2:
ℕ→ →ℚ
Hier hat man zunächst und dann ganz ℚ.
m p
Die Subtraktion − ist uneingeschränkt möglich.
n n
Sehr wichtig: Bisher war in Schulbüchern der Weg 1 der Standardweg; gerade in
Schulbüchern zum G 8 (Durchlaufen des Gymnasiums in 8 Jahren) wird
zunehmend auch der Weg 2 beschritten.
Ein weiterer (mathematischer) Aspekt zur Einführung der Subtraktion:
Subtraktion als Umkehrung der Addition
In der Menge der natürlichen Zahlen oder der Menge der ganzen Zahlen
wird die eindeutige Lösung der Gleichung a + x = b (wobei a, b ∈ oder a, b ∈ )
durch b − a gegeben.
(1) Analog wird in in der Menge der positiven Bruchzahlen + die eindeutige
p
m
m p
p m
Lösung der Gleichung
+x=
durch
−
gegeben, falls < .
n
n
n n
n n
(2) Analog wird in in der Menge der Bruchzahlen
die eindeutige Lösung der
p
m
m p
Gleichung
+x=
durch
−
gegeben.
n
n
n n
Sowohl im Fall (1) als auch im Fall (2) erhält man aufgrund der Regel zur Addition
m− p
m p m− p
x=
. Damit ergibt sich dann wegen der Eindeutigkeit
− =
.
n
n n
n
Beispiel für den Fall, dass der Zahlbereich + vorhanden ist [Fall (1)]:
9 3
3
9
−
wird die Gleichung + x =
betrachtet.
Zur Lösung der Aufgabe
11 11
11
11
6
9 3 6
Mit der Regel zur Addition in + erhält man x =
. Also gilt
− =
.
11
11 11 11
Beispiel für den Fall, dass der Zahlbereich
vorhanden ist [Fall (2)]:
5 7
7
5
Zur Lösung der Aufgabe −
wird die Gleichung
+x=
betrachtet.
13 13
13
13
−2
5 7 −2
Mit der Regel zur Addition in
erhält man x =
. Also gilt
− =
.
13
13 13 13
2.7.3 Gemischte Zahlen
Welche Fälle können auftreten? Abfolge im Schwierigkeitsgrad:
(1)
(2)
Gemischte Zahl minus natürliche Zahl 5 − 2
Subtraktion zweier gemischter Zahlen:
(3)
Gleiche Nenner, ohne Umwandlung 5 − 2
Subtraktion zweier gemischter Zahlen:
Verschiedene Nenner, ohne Umwandlung 5 − 2
(4)
(5)
Natürliche Zahl minus gemischte Zahl 8 − 2
Subtraktion zweier gemischter Zahlen:
Beliebige Nenner, mit Umwandlung 6 − 2
Fälle (1), (2), (3), (4) sind klar.
Schönes Schulbuchbeispiel zu Fall (5) [Siehe F. Padberg: Abschnitt III.8.4]:
2.7.4 Schwierigkeitsfaktoren
Es treten dieselben Schwierigkeitsfaktoren wie bei der Addition auf (siehe
Abschnitt 2.6.4).
2.7.5 Problembereiche
A Problembereich: Bruch minus Bruch
Fehlerstrategie:
a c a−c
S I:
− =
b d b−d
[Zähler – Zähler / Nenner – Nenner]
Bezüglich der Ursachen und der Therapie können völlig analoge Gesichtspunkte
angeführt werden wie in Abschnitt 2.6.5, Teil A.
B Problembereich:
Kombinierter Fall (Natürliche Zahl minus Bruch)
Fehlerstrategien:
a n−a
S II:
n− =
b
b
a n−a
S III:
n− =
b n−b
[
- Verführer – Fehler]
[Einbettungsfehler]
Bezüglich der Ursachen und der Therapie kann völlig analoge Gesichtspunkte
angeführt werden wie in Abschnitt 2.6.5, Teil B.