4.4 Implementierung von Bäumen 4.4.1 Implementierung

4.4 Implementierung von Bäumen
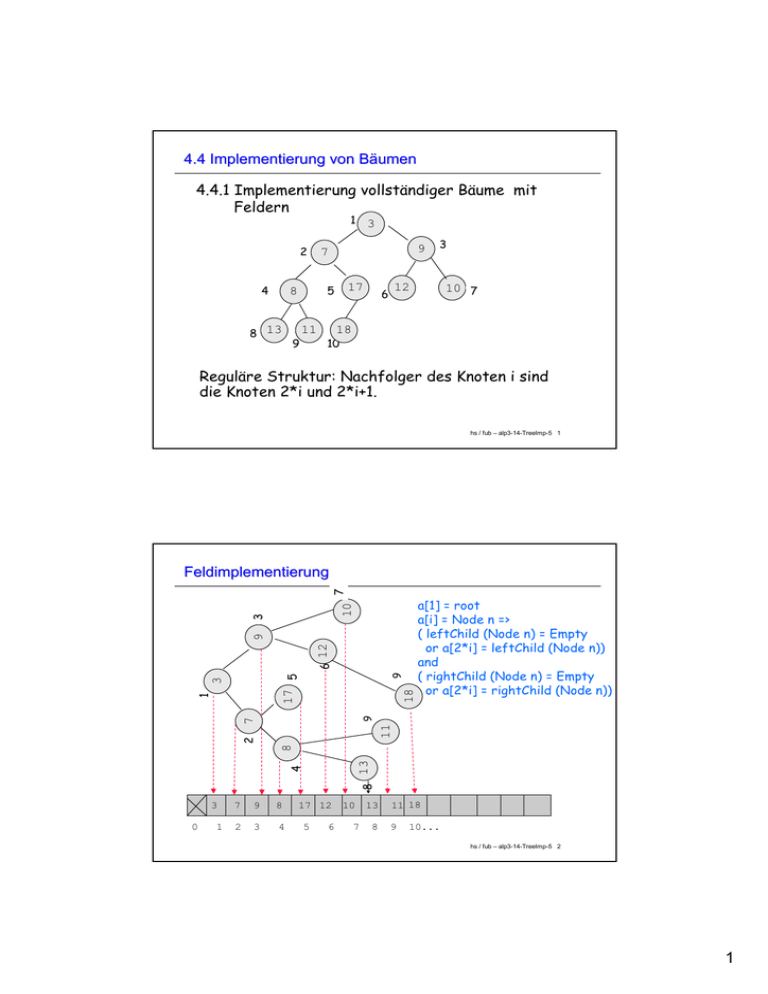
4.4.1 Implementierung vollständiger Bäume mit
Feldern
1 3
2
4
5
8
8 13
9
7
11
9
17
3
10 7
12
6
18
10
Reguläre Struktur: Nachfolger des Knoten i sind
die Knoten 2*i und 2*i+1.
hs / fub – alp3-14-TreeImp-5 1
18
a[1] = root
a[i] = Node n =>
( leftChild (Node n) = Empty
or a[2*i] = leftChild (Node n))
and
( rightChild (Node n) = Empty
or a[2*i] = rightChild (Node n))
4
8 13
8
2
11
7
9
1
3
17 5
9
6 12
9
3
10
7
Feldimplementierung
3
0
1
7
9
8
2
3
4
17 12
5
6
10
7
13
8
11 18
9
10...
hs / fub – alp3-14-TreeImp-5 2
1
Feldrepräsentation
public class BTArray {
// model: data Ord t => BTree t = E | N(BTree t) t
//
(BTree t)
// inv : true
Object [] a;
// the array implementing the tree
private int size;
//number of nodes
private int lgth;
//a.length
private int current;
// the current node
private final
int
ROOT = 1;
// the root
hs / fub – alp3-14-TreeImp-5 3
Abstraktionsfunktion und Invariante
Abstraktionsfunktion:
welchem abstrakten Baum entspricht eine
Baumrepräsentation durch ein Feld?
- Struktur
- Werte : Object -> t
// abstr: abstr :: (Object arrayT) -> BTree t
// abstr a = if (count==0) = E
// abstr a = abstr' 1
//
where abstr'' :: Object -> t
//
abstr' :: {1..lgth-1} -> BTree t
//
abstr' i = if (a[i] == null ) E
//
abstr' i
//
= N (abstr' (2*i) (abstr'' a[i])
//
(abstr (2*i+1)
hs / fub – alp3-14-TreeImp-5 4
2
Invariante
Repräsentationsinvariante: welche Feldwerte sind
erlaubt?
- erstes Feldelement nicht genutzt
- Größe des Baums immer kleiner Feldlänge
- Baumeigenschaft "zusammenhängender Graph"
// inv: a[0] == null
//
& size < lgth
//
& for all 1 <= i <= lgth
//
i !=1 & a[i] != null
=> a[i div 2] != null
hs / fub – alp3-14-TreeImp-5 5
Operationen
BTArray(int s ) {
// pre: lgth = power of 2
size = 0;
lgth = s-1;
a = new Object[lgth];
current = 1;
}
public BinTree left()throws.....{
// pre: a[current] != null & 2*current < lgth
// effects: current = current * 2
if (2*current > size)
throw ........
else current = 2*current;
return this;
}
hs / fub – alp3-14-TreeImp-5 6
3
Operationen
public BinTree parent(){
// pre: current != 1
// effects: current = current div 2
current = current/2;
return this;
}
public void setVal(Object o){
// pre: current < lgth
a[current] = o;
}
public Object root(){
// pre: current != 0
return a[current];
hs / fub – alp3-14-TreeImp-5 7
Traversierung
public void preorderTraverse(Func f) {
preOrder(ROOT, f);
}
// uses array representation
private void preOrder(int i, Func f) {
if (i > a.length) return;
if (a[i] == null) return;
f.call(a[i]);
preOrder (2*i,f);
preOrder (2*i+1,f);
}
Iterator?
Was heißt "next()" in einem Baum?
hs / fub – alp3-14-TreeImp-5 8
4
4.4.2 Implementierung durch verketteten Baum
- direkte Implementierung:
BinTree1 {
- val
- left
- right
BinTree1 {
- val
- left
- right
BinTree1 r
BinTree1 {
- val
- left
- right
hs / fub – alp3-14-TreeImp-5 9
Binärbaum: Erste Implementierung
class BinTree1 implements BinTree{
Object val;
BinTree1 left, right;
// abstr(null) = E
// abstr (val, left, right) =
//
N((abstr left) val (abstr right))
public BinTree1 (BinTree1 l, Object o, BinTree1 r){
val
= o;
left
= l;
right
= r;
}
public Object val() {
return val;
}
hs / fub – alp3-14-TreeImp-5 10
5
Binärbaum: Erste Implementierung
public BinTree1 left() {
return left;
}
...
public boolean isEmpty(BinTree1 b){
return (b==null);
}
public boolean isEmpty(){} //cannot be applied to this
public boolean isLeaf(){
return (isEmpty(left) && isEmpty(right);
}
public void postorderPrint(){
if (!isLeaf()){
left.postorder();
right.postorder();
// process value;
System.out.print(val); }
}}
hs / fub – alp3-14-TreeImp-5 11
4.4.3 Implementierung mit Knoten-Objekten
BinaryTree
root ---->
lft val
BinaryTree
lft val
r
TreeNode
lft val
r
r
r
lft val
r
hs / fub – alp3-14-TreeImp-5 12
6
Knotenobjekte
class TreeNode {
Object val ;
TreeNode left = null, right = null;
public TreeNode (Object e) { val = e; }
public TreeNode left () { return left; }
public TreeNode right () { return right; }
public Object
val() { return val; }
public boolean isLeaf ()
{ return left == null && right == null;
public void setLeft (TreeNode n) { left = n; }
public void setRight (TreeNode n) { right = n; }
}
}
hs / fub – alp3-14-TreeImp-5 13
Binärbaum
class BinaryTree {
protected TreeNode root = null;
private int size = 0;
public BinaryTree() {}
public BinaryTree (Object val){
root=new TreeNode(val);
}
public TreeNode left() {
current = root.left();
}
Implementiert nicht
public Object val() {
BinTree – Interface.
return root.val();
} ....
hs / fub – alp3-14-TreeImp-5 14
7
InorderInorder-Iterator
Iterator-Interface:
next(), hasNext()
Problem: "nächster Knoten" ist nicht notwendig
"lokal":
a
c
b
d
x
y
e
....
Wenn a aktuell:
next() -> y
....
Wenn x aktuell:
next -> z
z
hs / fub – alp3-14-TreeImp-5 15
InorderInorder-Iterator für Binärbaum (1)
protected class BTreeIteratorInOrd implements
java.util.Iterator {
private Stack stack;
public BTreeIteratorInOrd (BinaryTree tree) {
stack = new StackArray();
TreeNode node = tree.root ();
while (node != null) {
stack.push (node);
node = node.left ();
}
}
public boolean hasNext () {
return !stack.isEmpty ();
}
hs / fub – alp3-14-TreeImp-5 16
8
InorderInorder-Iterator für Binärbaum (1)
public Object next () {
TreeNode node = (TreeNode) stack.pop ();
Object o = node.val ();
if (node.right () != null) {
node = node.right ();
while (node != null) {
stack.push (node);
node = node.left ();
}
}
return o;
}
public void remove () {
throw new UnsupportedOperationException ();
}
}
hs / fub – alp3-14-TreeImp-5 17
Ordnung auf Bäumen
Kann
man Bäume ordnen?
ja, wenn die Knotenwerte geordnet sind.
Vergleiche lexikographische Ordnung:
aabcdef < aabcedf
abcd
< abcde
Ordnungsrelation auf Binärbäumen
S, T Binärbäume.
S < T ! T.isEmpty() and
! S.isEmpty() and
S.val = T.val and
S.left =T.left and
(S.isEmpty
or
( S.val < T.val or
(S.left < T.left or
S.right < T.right)))
Was heißt
"=" ??
hs / fub – alp3-14-TreeImp-5 18
9
4.4.4 Binärbaum mit Rückverweisen
... vereinfachen
manche
Algorithmen...?
Abb.: aus Tamassia:
DS & Alg in Java
hs / fub – alp3-14-TreeImp-5 19
4.4.4 Binärbaum mit Rückverweisen
class BinTree2 {
Object val;
BinTree2 left, right, prev;
public BinTree2 (BinTree2 l, Object o, BinTree2 r){
val = o;
left = l;
Verweis auf Elternknoten,
right = r;
manchmal nützlich, ...
prev = null;
aber
}
(Inorder-) Traversierung??
....
public void setLeft(BinTree2 b){
left = b;
b.prev = this;
}...}
hs / fub – alp3-14-TreeImp-5 20
10
4.4.5 Gefädelter Binärbaum (Threaded
(Threaded Tree)
Tree)
a
b
c
d
e
h
f
g
i
Hier: Inorder-Faden
Beachte: keine zusätzlichen Vorwärtsverweise,
Rückverweise nur von "tieferer auf höhere Ebene"
hs / fub – alp3-14-TreeImp-5 21
4.4.6 nn-ärer Baum
class KTree {
int MAXSUCC = 5;
Object val;
KTree[] succ=null;
Direkte Implementierung
der rekursiven Definition
public KTree ( Object o){
val = o;
}
public boolean isLeaf()
{return succ==null;}
public KTree nth(int n) {
// pre: n >= 0 && succ != null
if (n < MAXSUCC) return succ[n];
else throw IllegalArityException;
} ....
}
hs / fub – alp3-14-TreeImp-5 22
11
4.4.7 Mehrwegbäume als binäre Bäume
Variante
A: Liste von Nachfolgern
class MTree1
{
Object val;
LinkedList successors;
....
Variante
B: Zurückführen auf Binärbaum
Verweise nicht auf Kinder sondern auf
- erstes Kind
- Geschwister
hs / fub – alp3-14-TreeImp-5 23
Mehrwegbäume als binäre Bäume
a
b
e
j
k
g
f
l
d
c
h
i
m
hs / fub – alp3-14-TreeImp-5 24
12
Mehrwegbäume als binäre Bäume
Datenstruktur identisch, andere Operationen (und
Algorithmen)
class MTree
{
Object val;
MTree first, nextSibling;
public MTree (Object o) {val=o;}
public Object findNthChild(int n){
....
...}
hs / fub – alp3-14-TreeImp-5 25
13