Temperaturabhängige Widerstände - public.fh

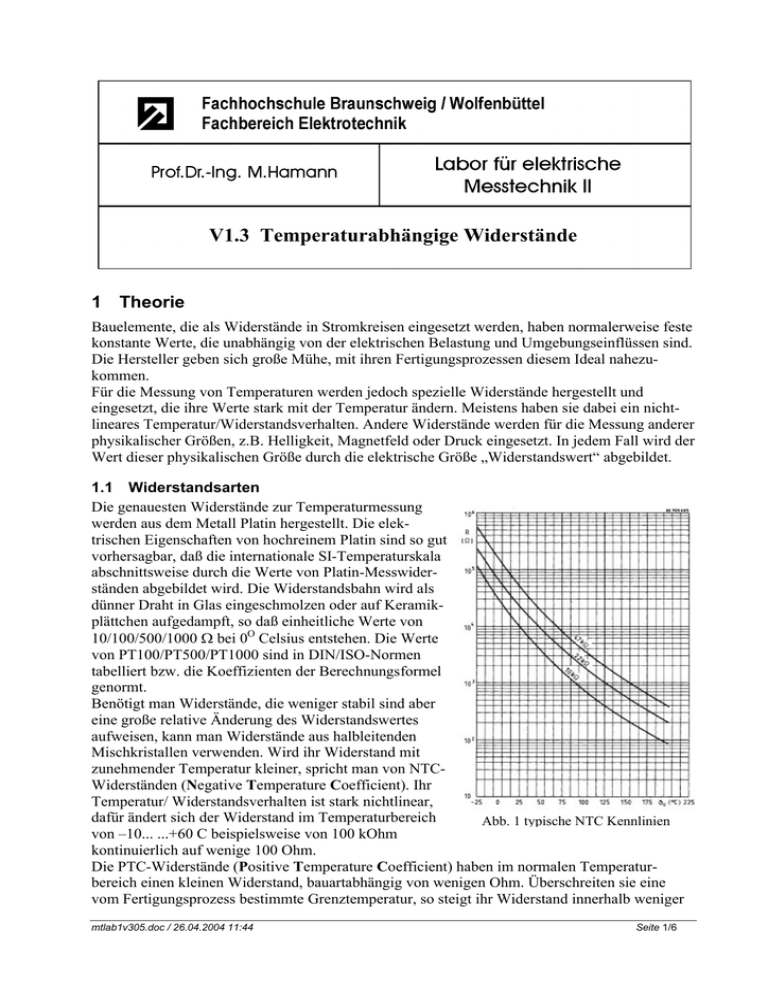
V1.3 Temperaturabhängige Widerstände
1 Theorie
Bauelemente, die als Widerstände in Stromkreisen eingesetzt werden, haben normalerweise feste
konstante Werte, die unabhängig von der elektrischen Belastung und Umgebungseinflüssen sind.
Die Hersteller geben sich große Mühe, mit ihren Fertigungsprozessen diesem Ideal nahezukommen.
Für die Messung von Temperaturen werden jedoch spezielle Widerstände hergestellt und
eingesetzt, die ihre Werte stark mit der Temperatur ändern. Meistens haben sie dabei ein nichtlineares Temperatur/Widerstandsverhalten. Andere Widerstände werden für die Messung anderer
physikalischer Größen, z.B. Helligkeit, Magnetfeld oder Druck eingesetzt. In jedem Fall wird der
Wert dieser physikalischen Größe durch die elektrische Größe „Widerstandswert“ abgebildet.
1.1 Widerstandsarten
Die genauesten Widerstände zur Temperaturmessung
werden aus dem Metall Platin hergestellt. Die elektrischen Eigenschaften von hochreinem Platin sind so gut
vorhersagbar, daß die internationale SI-Temperaturskala
abschnittsweise durch die Werte von Platin-Messwiderständen abgebildet wird. Die Widerstandsbahn wird als
dünner Draht in Glas eingeschmolzen oder auf Keramikplättchen aufgedampft, so daß einheitliche Werte von
10/100/500/1000 Ω bei 0O Celsius entstehen. Die Werte
von PT100/PT500/PT1000 sind in DIN/ISO-Normen
tabelliert bzw. die Koeffizienten der Berechnungsformel
genormt.
Benötigt man Widerstände, die weniger stabil sind aber
eine große relative Änderung des Widerstandswertes
aufweisen, kann man Widerstände aus halbleitenden
Mischkristallen verwenden. Wird ihr Widerstand mit
zunehmender Temperatur kleiner, spricht man von NTCWiderständen (Negative Temperature Coefficient). Ihr
Temperatur/ Widerstandsverhalten ist stark nichtlinear,
dafür ändert sich der Widerstand im Temperaturbereich
Abb. 1 typische NTC Kennlinien
von –10... ...+60 C beispielsweise von 100 kOhm
kontinuierlich auf wenige 100 Ohm.
Die PTC-Widerstände (Positive Temperature Coefficient) haben im normalen Temperaturbereich einen kleinen Widerstand, bauartabhängig von wenigen Ohm. Überschreiten sie eine
vom Fertigungsprozess bestimmte Grenztemperatur, so steigt ihr Widerstand innerhalb weniger
mtlab1v305.doc / 26.04.2004 11:44
Seite 1/6
Temperaturabhängige Widerstände
Grad Änderung um mehrere Zehnerpotenzen an. Sie werden zur Übertemperaturabschaltung
(Motorschutzschalter) oder als „dauerfeste Sicherung“ eingesetzt.
Eine höhere Stabilität und Wiederholbarkeit des Widerstandsverhaltens bei günstigem Preis
weisen Halbleiter-Widerstände auf, die mit IC-Herstellprozessen auf Silizium-Wafern produziert
werden. Sie haben einen gut reproduzierbaren positiven Temperaturkoeffizienten bei einigermaßen linearem Widerstandsverhalten.
An Stelle von Widerständen wird häufig zur Temperaturmessung die Durchlassspannung eines
pn-Übergangs in einer Diode oder einem Transistor verwendet (z.B. Pentium-Chiptemperatur).
Bei konstantem Stromfluß hat diese Spannung einen konstanten negativen Temperaturkoeffizient
von ca. –2,2 mV / Celsius.
1.2 Linearisierung
(1) Das Verhalten von Platinwiderständen bei Temperatur ist sehr genau bekannt und folgt für
den Bereich der Temperatur T von 0 OC bis 660 OC der Beziehung
R (T ) = R (0) ⋅ (1 + A ⋅ T + B ⋅ T 2 )
mit
A = 3,85055 ⋅10 − 3 ; B = −5,7750 ⋅ 10− 7 ; T in [C ] ;
Dabei ist meistens der Einfluß des Koeffizienten B schon vernachlässigbar klein. Damit ist die
Widerstandsänderung eines PT100/1000 näherungsweise linear.
(2) Das Widerstandsverhalten der NTC-Widerstände folgt in guter Näherung der Gleichung
R (T ) = R 25 ⋅ e B (1 / T −1 / T ) ; T , TN in [ K ]
N
mit den Datenblatt-Angaben für R25 [Ω, kΩ] und die Materialkonstante B [3000...4500 K, typabhängig ]. Durch die Parallel-Schaltung eines festen Widerstandes RP wird zwar die Empfindlichkeit des Sensors reduziert, der Widerstandsverlauf
aber für einen kleinen Bereich einigermaßen
linearisiert. Das geschieht am besten, wenn man sich
auf den Sensorwiderstand in der Mitte des Linearisierungsbereichs bei der Temperatur TM [K] bezieht.
RP = R(TM ) ⋅
B − 2TM
; T , TM in [ K ]
B + 2TM
(3) Die Kennlinie eines Kaltleiters ist stark nichtlinear
und wird durch den Herstellprozess bestimmt. Ein
niedriger Widerstandswert unterhalb der Schwelle, ein
rascher Übergang und ein großer Wert bei hoher
Temperatur ist erwünscht.
(4) Die Halbleiter-Temperatursensoren KTY-84
arbeiten nach dem Prinzip des radialen AusbreitungsWiderstandes (Spreading Resistance) in einem
Silizium-Kristall, dessen zwei gegenüberliegende
Elektroden auf einer Seite flächig metallisiert sind. Auf
der anderen Seite bildet ein kleiner kreisförmiger
Kontakt von ca. 20 µm Durchmesser die GegenAbb. 2 Kennlinie eines PTC Widerstands
elektrode. Zwischen beiden Elektroden entsteht eine
pyramidenförmige Stromverteilung im Kristall, die den Einfluss der Fertigungstoleranzen des
Kristalls erheblich reduziert. Sie haben einen Nominalwiderstand von 1000 Ω bei 100 OC und
mtlab1v305.doc / 26.04.2004 11:44
Seite 2 /6
Temperaturabhängige Widerstände
einen positiven Temperaturkoeffizienten von 0,61%/K. Aufgrund ihrer hohen Genauigkeit und
der hervorragenden Langzeitstabilität bei Temperaturen bis 300 OC stellen diese SiliziumBauelemente eine ausgezeichnete Alternative zu den herkömmlichen Sensoren in NTC- oder
PTC-Technologie dar.
(5) Speist man einen Halbleiter-pn-Übergang mit einem
konstanten Strom, hängt die Durchlaßspannung nur von der
Sperrschicht-Temperatur ab. Der Einfluß des Durchlaßwiderstandes einer Diode bei sich änderndem Speisestrom läßt sich
durch einen Transistor mit verbundenem Basis- und Kollektoranschluß verringern, weil da nur der Basis-Bahnwiderstand mit
dem geringen Basis-Strom des Transistors wirkt. In beiden
Fällen ändert sich bei einem Durchlaßstrom von etwa 0,5 mA die Abb. 3 pn-Übergang als Sensor
Durchlaßspannung UA von ca. 0,6 Volt um konstante -2,2 mV / OC.
1.3 Peltier-Element-Kühler
Berühren sich zwei unterschiedliche Metalle oder Metall-Legierungen, so gehen aufgrund der
thermischen Bewegung Elektronen aus dem Metall mit geringerer Austrittsarbeit in das Metall
höherer Austrittsarbeit über. Das erste Metall lädt sich positiv gegenüber dem zweiten auf, es
entsteht eine Kontaktspannung. In einem verbundenen Stromkreis würde dennoch kein Strom
fließen, weil die Spannungen entgegengerichtet gleich groß
sind. Haben die Berührungsstellen jedoch unterschiedliche
Temperaturen, so sind die Kontaktspannungen unterschiedlich groß, es kann ein Strom fließen. Dies ist der
thermoelektrische oder Seebeck-Effekt, der bei Thermoelementen zur Temperaturmessung eingesetzt wird.
Die Umkehrung dieses Effektes ist der Peltier-Effekt.
Fließt ein Strom durch die Kontaktstelle zweier geeigneter
Metalle, so entsteht je nach Stromrichtung eine Abkühlung
oder Erwärmung. Dieser gerichteten Erwärmung ist jedoch
immer die Joul´sche Verlustwärme des Peltier-Elements
überlagert, was den geringen Wirkungsgrad der
Komponente bewirkt. Die transportierte Wärmemenge und
die Verlustwärme müssen mit einem Kühlkörper oder
Abb. 4 Peltier Kühler
Ventilator an die Umgebung abgeführt werden. Übliche
Peltierelemente arbeiten bei Temperaturdifferenzen bis 70 OC zwischen warmer und kalter Seite,
sie benötigen je nach Baugröße Spannungen bis 10 Volt bei Strömen bis zu 5 Ampere.
1.4 Messungen in einer Brückenschaltung
Widerstandssensoren gehören zu den Sensoren, die nicht bei einer Messgröße null auch den
Wert null abgeben, vielmehr ändert sich ihr Wert ausgehend von einem festen Anfangswert R0.
Damit können sie gut in einer Brückenschaltung eingesetzt werden.
Will man Präzisionsmessungen z.B. mit den Platin-Messwiderständen durchführen, spielt wegen
der geringen temperaturabhängigen Widerstandsänderung der Widerstand der Zuleitung zum
Messfühler bereits eine wesentliche Rolle. Ein Zuleitungswiderstand von 1Ω in Reihe mit einem
PT100 führt bei einer Widerstandsänderung von 0,38 Ω/ OC zu einem systematischen Messfehler
von 2,6 OC. Deswegen muß der Zuleitungswiderstand abgeglichen oder durch Zusatzschaltungen
kompensiert werden.
mtlab1v305.doc / 26.04.2004 11:44
Seite 3 /6
Temperaturabhängige Widerstände
Eine häufig angewandte Methode ist die Dreileiter-Schaltung, bei der an den 2 Anschlüssen des
Messwiderstands 3 Leitungen (1x und 2x) angeschlossen werden. Durch diese Anschlußart ist es
möglich, den Strom im Brückenzweig durch R1, R2
zu trennen vom Anzeigestrom , der in der
Brückendiagonalen AB fließt.
Es wird angenommen, die Leitungswiderstände
RL1..RL3 wären gleich groß und zeigen gleiches
Verhalten bei Temperaturänderungen. Dann wird R2
um RL1 vergrößert, R1 um RL3. Dadurch ändern sich
zwar die absoluten Werte, das Verhältnis der
Widerstände im Brückenzweig als Quelle der
Spannung UA
UA = U 0 ⋅ (
R1 + RL3
)
R1 + RL3 + R 2 + RL1
Abb. 5 Brücke mit Dreileiter-Schaltung
ändert sich in der abgeglichenen Brücke (Verändern
von R2, bis UAB = 0) nicht, weil beide Teilwiderstände sich um denselben Betrag erhöhen. Die
Temperaturwiderstandsmessung R1, R2 wird also durch einen Leitungswiderstand RL nicht
verfälscht.
Der Leitungswiderstand RL2 kann vernachlässigt werden, weil in der Brückendiagonalen im
abgeglichenen Zustand kein oder nur ein geringer Strom fließt, der die Spannungsmessung UAB
nicht verfälscht.
Eine Alternative bildet die Vierleiter-Schaltung, bei der der Messfühler mit einem konstanten
Strom IQ gespeist wird und über die beiden weiteren Leitungen der Spannungsabfall direkt am
Sensor gemessen wird.
Die Stromquelle erzwingt einen immer gleichen
Strom durch den Messwiderstand R1 unabhängig von den Leitungswiderständen RL1, RL4.
Solange der Strom bei der Spannungsmessung
UR vernachlässigbar klein ist (hoher Eingangswiderstand des Instrumentes oder Verstärkers)
kann unabhängig von der Größe von RL2, RL3
die Spannung am Widerstand R1 unverfälscht
gemessen.
Für die Messung sehr kleiner Änderungen muß
für die Messung von ∆UR ein KompensationsAbb. 6 Messung in Vierleiter-Schaltung
verfahren eingesetzt werden.
Bei der Vierleiter-Schaltung werden Speisestromkreis und Messstromkreis mit getrennten
Leitungen am Sensor-Widerstand angeschlossen.
mtlab1v305.doc / 26.04.2004 11:44
Seite 4 /6
V1.3 Temperaturabhängige Widerstände
2 Vorbereitung
Für den Versuch sind mehrere unterschiedliche Widerstände und ein Diodenelement auf dem
Peltier-Kühler und –Heizer montiert. Die „wirkliche“ Temperatur der Kupferplatte kann nur mit
einem der Widerstände, dem PT1000 Widerstand gemessen werden.
(1) Bereiten Sie für die Messungen Tabellen vor, die Messungen von 4 Widerständen und einer
(Dioden-) Spannung alle 5 OC von 10 OC bis 75 OC vorsehen. Ermitteln Sie zu diesen
Temperaturen die zu erwartenden Widerstände des PT1000 Elements als Referenzwert und
tragen sie schon in Ihre Tabelle ein.
(2) Ermitteln Sie durch Rechnung einen Parallelwiderstand RP zu dem NTC-Heißleiter für eine
Mitteltemperatur des Linearitätsbereichs von TM = 40 OC, wenn es sich bei dem Widerstand
um ein Bauteil mit R25 = 47 kOhm und einem B = 4400 handelt.
Für die Siedepunktsbestimmung wird ein PT100-Widerstand in 3-Leiter-Schaltung eingesetzt.
Zur Nachbildung der Leitungswiderstände werden wahlweise 4,3 Ω-Widerstände eingesetzt.
(3) Entwerfen Sie eine Messbrückenschaltung entsprechend Abb. 5 mit R1 als PT100, R2 als
Widerstandsdekade, R3..R4 als Präzisionswiderstände, Speisespannung U0 = 5 V, ein
Voltmeter als Nullpunktindikator.
(4) Ermitteln Sie den zu erwartenden Messfehler ∆T beim Siedepunkt von Wasser, wenn ohne
Dreileiterschaltung unbemerkt ein zusätzlicher Leitungswiderstand von jeweils RL = 4,3 Ω
für die Hin- und Rückleitung existieren würde.
(5) Bereiten Sie eine Tabelle für zwei Messreihen mit einer Brückenschaltung vor, bei denen
jeweils der Wert des PT100-Widerstands, der Wert des Kompensationswiderstands R2, die
damit gemessene Wassertemperatur und die Zeit [~15 min] aufgezeichnet wird.
3 Durchführung
3.1 Kennlinien von Temperaturmesswiderständen
Stellen Sie an einer Widerstandsdekade den von Ihnen ermittelten Wert des Parallelwiderstandes
RP ein, kontrollieren den Wert und stellen das Gerät mit Anschlußkabeln bereit.
mtlab1v305.doc / 26.04.2004 11:44
Seite 5/6
Temperaturabhängige Widerstände
Schließen Sie das Netzgerät für das Peltier-Element so an, daß es zuerst kühlt (LED grün).
Schließen Sie für die Widerstandsmessung und Spannungsmessung an dem pn-Übergang jeweils
ein Multimeter im geeigneten Messbereich an.
Schalten Sie zuerst das Peltier-Steuergerät an und prüfen die Funktion der angeschlossenen
Messgeräte. Die angezeigten Werte müssen denen bei Raumtemperatur entsprechen.
Drehen Sie den Spannungsregler des Netzgerätes zuerst auf kleine Werte und schalten das
Netzgerät ein. Am Widerstand des PT1000 Sensors läßt sich eine Änderung der Temperatur der
Peltier-Platte mit kleiner Verzögerung erkennen.
Durch vorsichtiges Verändern der Peltierspannung fahren Sie den gewünschten nächsten
Temperaturpunkt an. Berücksichtigen Sie die thermische Einschwingzeit der Versuchsanordnung. Regeln Sie den Wert der Heiz- / Kühlspannung so ein, daß die gewünschte
Temperatur näherungsweise für den Ablesezeitraum stabil ist.
Lesen Sie die Messwerte für die Widerstände und Spannungen bei der eingestellten Temperatur
ab. Nach dem Messen des NTC-Widerstandes allein schalten Sie kurz Ihren gewählten RP
parallel und notieren ebenfalls den Widerstandswert der Parallelschaltung.
Nach dem Abarbeiten der Messpunkte, bei denen Kühlung erforderlich ist, schalten Sie die
Peltierspannung auf „Heizen“ um und fahren entsprechend die wärmeren Messpunkte an.
3.2 Bestimmung des Siedepunkts von Wasser
Bauen Sie am Laborplatz eine Brückenschaltung entsprechend Ihrem Entwurf auf. Zur Messung
der Diagonalspannung wird ein Digitalvoltmeter eingesetzt. Sorgen Sie dafür, daß der Wasserkocher zu etwa 1/2..3/4 mit Wasser gefüllt ist.
In der ersten Messung wird die Aufheizkurve bei vernachlässigbar kleinem Leitungswiderstand
gemessen, bei der Wiederholungsmessung mit einem Wert RL1...3 = 4,3 Ω.
Stellen Sie an der Widerstandsdekade einen Wert für R2 ein, so dass die Brückenschaltung bei
der Wassertemperatur T = 50 OC abgeglichen ist. Die Messzeit beginnt bei dieser Temperatur.
Messen Sie durch Nachstellen der Widerstandsdekade den Zeitpunkt [min] für die Temperaturen
von 50/60/70/80/90/95/“100“ OC und die Siedetemperatur. Schalten Sie gegebenfalls den Kocher
ein zweites Mal ein.
Führen Sie die Messung nach einem Abkühlen des Wassers ein zweites Mal durch, jedoch mit
den 3 „Leitungswiderständen“ in Reihe mit den Anschlüssen des PT100-Sensors.
4 Auswertung
(1) Tragen Sie Ihre gemessenen Werte für den NTC- und PTC-Widerstand in ein lineares (1)
und ein halblogarithmisches Diagramm (2) ähnlich Abb.1 ein.
(2) Normieren Sie Ihre Messwerte aller Sensoren so, daß ihr Wert bei 25 OC entsprechend 1,00
ist und tragen dazu den relativen Verlauf in ein lineares Diagramm (3) ein.
(3) Berechnen oder ermitteln Sie für den linearisierten NTC-Widerstand und die Diodendurchlaßspannung eine idealisierte Ausgleichsgerade (Tangente im Bereich von 40 OC).
Berechnen und zeichnen Sie jeweils ein Diagramm (4,5) für die Abweichung Ihrer
Messpunkte von dieser Ideallinie im Bereich von +10 ..70 OC als +/- ∆T(T), indem Sie die
berechnete Ersatzgerade idealisiert in die x-Achse drehen, die +/- ∆T der Messwerte sinnvoll
skaliert als positive oder negative Werte nach oben / unten auftragen und die Punkte mit
einer stetigen Ausgleichsfunktion verbinden.
(4) Zeichnen Sie in ein T/t-Diagramm den Aufheiz-Zeitverlauf des Wasserkochers ohne und mit
Leitungswiderstand .
(5) Berechnen Sie jeweils den Siedepunkt des Wassers. Warum können Abweichungen vom
Idealwert auftreten (kurz) ?
mtlab1v305.doc / 26.04.2004 11:44
Seite 6 /6