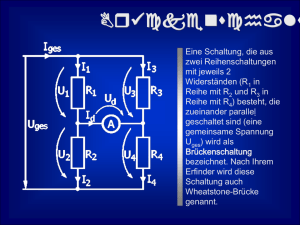
Wheatston`sche Brückenschaltung

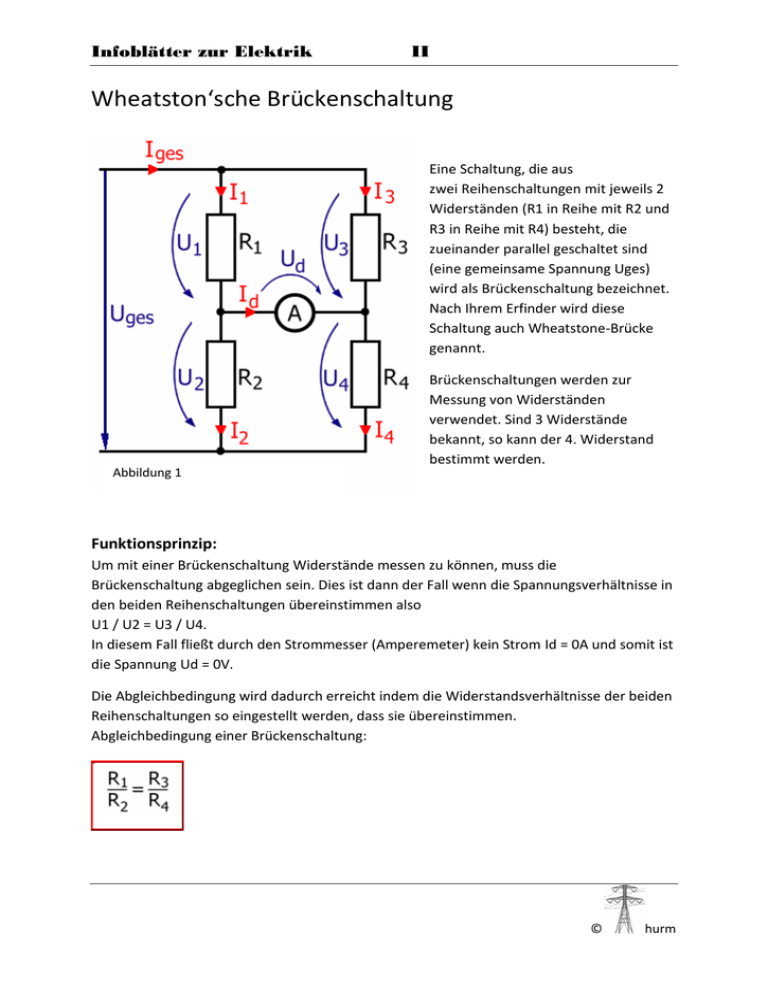
Infoblätter zur Elektrik
II
Wheatston‘sche Brückenschaltung
Eine Schaltung, die aus
zwei Reihenschaltungen mit jeweils 2
Widerständen (R1 in Reihe mit R2 und
R3 in Reihe mit R4) besteht, die
zueinander parallel geschaltet sind
(eine gemeinsame Spannung Uges)
wird als Brückenschaltung bezeichnet.
Nach Ihrem Erfinder wird diese
Schaltung auch Wheatstone-Brücke
genannt.
Abbildung 1
Brückenschaltungen werden zur
Messung von Widerständen
verwendet. Sind 3 Widerstände
bekannt, so kann der 4. Widerstand
bestimmt werden.
Funktionsprinzip:
Um mit einer Brückenschaltung Widerstände messen zu können, muss die
Brückenschaltung abgeglichen sein. Dies ist dann der Fall wenn die Spannungsverhältnisse in
den beiden Reihenschaltungen übereinstimmen also
U1 / U2 = U3 / U4.
In diesem Fall fließt durch den Strommesser (Amperemeter) kein Strom Id = 0A und somit ist
die Spannung Ud = 0V.
Die Abgleichbedingung wird dadurch erreicht indem die Widerstandsverhältnisse der beiden
Reihenschaltungen so eingestellt werden, dass sie übereinstimmen.
Abgleichbedingung einer Brückenschaltung:
©
hurm
Infoblätter zur Elektrik
II
Herleitung
Im abgeglichenen Zustand fließt durch den Strommesser kein Strom, daher können für die
beiden Stromzweige R1-R2 und R3-R4 die Gesetze der Reihenschaltung angewendet werden.
U1 = R1 · I1
Bei einer Reihenschaltung ist I1 = I2 daher berechnet sich U2 gemäß der Formel:
U2 = R2 · I1
Für die Reihenschaltung R3-R4 gilt entsprechend:
U3 = R3 · I3
U4 = R4 · I3
setzt man die Spannungen der beiden Reihenschaltungen zueinander ins Verhältnis so ergibt
sich:
(R1 · I1) / (R2 · I1) = (R3 · I3) / (R4 · I3)
durch Kürzen der Ströme erhält man die oben stehende Formel
Messung von Widerständen bei einer Brückenschaltung
Soll ein unbekannter Widerstand z.B. R4 ermittelt werden, so muss die Gleichung
entsprechend umgestellt werden:
R4 = (R2 · R3) / R1
Zur Messung eines unbekannten Widerstandes mit einer Brückenschaltung kann nun ein
veränderlicher Widerstand (z.B. R1) so lange geändert werden bis die Brücke abgeglichen
(Id = 0A) ist. Anhand der nun bekannten 3 Widerstände (R1 bis R3) kann der 4. Widerstand
R4 berechnet werden. In der Praxis wird diese Art der Widerstandsmessung mit einem
speziellen Messgerät durchgeführt.
Die Widerstände R1 und R2 in der Abbildung 1 werden dafür durch einen Widerstandsdraht
aus Konstantan ersetzt, auf dem ein Schleifer angebracht
ist.
Mit Hilfe dieses Schleifers ist es möglich, den gesamten
Drahtwiderstand in die Widerstände R1 und R2 zu
unterteilen und hierdurch die Messbrücke abzugleichen.
Die Messbrücke ist wiederum abgeglichen, wenn das
Produkt der diagonal liegenden Widerstände gleich groß
ist.
Da der Widerstand R1 der Länge l1 und der Widerstand
R2 der Länge l2 proportional ist, lautet die
Abgleichbedingung für die Wheatstonesche Brücke
l2* R3 = l1* R4
bzw.
R4=(l2/l1)*R3
©
hurm
Infoblätter zur Elektrik
II
Übungsbeispiel 1:
Der Widerstand R4 in der Abbildung 1 ist unbekannt ( R4 = Rx )
R1 beträgt 16 Ω ( Festwiderstand )
R3 beträgt 50 Ω ( Festwiderstand )
R2 soll durch einen einstellbaren Widerstand ersetzt werden.
R2 muss auf 40 Ω eingestellt werden, damit die Brücke abgeglichen ist.
Wie groß ist der Widerstand Rx?
Lösung:
R1 * Rx = R2 * R3 bzw.
Rx = R2 * R3 / R1 = 40 Ω* 50 Ω/ 16 Ω= 125 Ω
Rx = 125 Ω
Übungsbeispiel 2:
Der Widerstandsdraht der Messbrücke in Abbildung 2 hat eine Gesamtlänge von 1m.
Der Widerstand R3 beträgt 50 Ω( Festwiderstand )
Der Widerstand R4 beträgt 30 Ω( Festwiderstand )
Wo muss der Schleifer stehen, damit die Messbrücke abgeglichen ist?
Lösung:
Abgleichbedingung
bzw.
d.h.
mit
folgt hieraus
bzw.
und entsprechend:
l1 * R4 = l2 * R3
l1 / l2 = R3 / R4 = 10 Ω/ 30 Ω= 1 : 3
l2 = 3 * l1 ( Gleichung 1 )
l1 + l2 = 1m ( Gleichung 2 )
l1 + 3 * l1 = 1m
l1 = 1/4 m = 25 cm
l2 = 75 cm
©
hurm