Operationsverstärker Tutorium

University of Applied
Sciences Cologne
Operationsverstärker
Tutorium
Invertierender Verstärker
OP-01
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Der Operationsverstärker wird in vielen elektronischen Systemen eingesetzt. Mit ihm können – je nach
Beschaltung – zahlreiche Operationen durchgeführt werden, angefangen vom einfachen Verstärker, über
Summieroperationen, Komparator, Differenzierer und Integrierer bis hin zu komplexeren Operationen
wie zum Beispiel bei INICs, UNICs sowie dem Gyrator.
In diesem Tutorium behandeln wir nur den Differenzierer und den Integrierer. Als Grundlage hierfür wird
der invertierende Verstärker herangezogen, der im Folgenden näher erklärt wird.
R2
i1
R1
iD
i2
uD
uE
uA
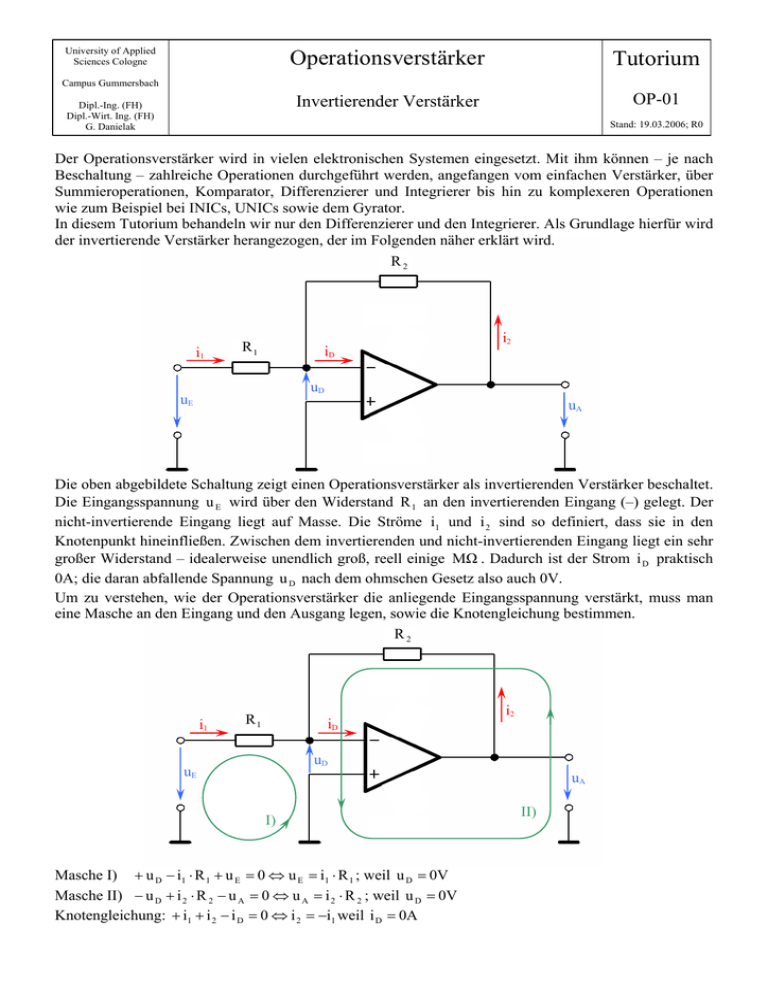
Die oben abgebildete Schaltung zeigt einen Operationsverstärker als invertierenden Verstärker beschaltet.
Die Eingangsspannung u E wird über den Widerstand R 1 an den invertierenden Eingang (–) gelegt. Der
nicht-invertierende Eingang liegt auf Masse. Die Ströme i1 und i 2 sind so definiert, dass sie in den
Knotenpunkt hineinfließen. Zwischen dem invertierenden und nicht-invertierenden Eingang liegt ein sehr
großer Widerstand – idealerweise unendlich groß, reell einige MΩ . Dadurch ist der Strom i D praktisch
0A; die daran abfallende Spannung u D nach dem ohmschen Gesetz also auch 0V.
Um zu verstehen, wie der Operationsverstärker die anliegende Eingangsspannung verstärkt, muss man
eine Masche an den Eingang und den Ausgang legen, sowie die Knotengleichung bestimmen.
R2
i1
R1
iD
i2
uD
uE
uA
I)
Masche I) + u D − i1 ⋅ R 1 + u E = 0 ⇔ u E = i1 ⋅ R 1 ; weil u D = 0V
Masche II) − u D + i 2 ⋅ R 2 − u A = 0 ⇔ u A = i 2 ⋅ R 2 ; weil u D = 0V
Knotengleichung: + i1 + i 2 − i D = 0 ⇔ i 2 = −i1 weil i D = 0A
II)
University of Applied
Sciences Cologne
Operationsverstärker
Tutorium
Invertierender Verstärker
OP-02
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
uE
. Diesen Strom kann man – bedingt
R1
durch den Zusammenhang i 2 = −i1 der Knotengleichung – in Gleichung II) einsetzen. Somit erhält man:
u
R
u A = i 2 ⋅ R 2 = −i1 ⋅ R 2 = − E ⋅ R 2 = − 2 ⋅ u E . Man hat also u A als eine Funktion von u E dargestellt. Der
R1
R
1231
V
Zusammenhang zwischen Eingangs- und Ausgangsspannung ist die Spannungsverstärkung
u
R
V = A = − 2 . Man erkennt, dass die Ausgangsspannung durch das negative Vorzeichen um 180°
uE
R1
R
verschoben (invertierender) und um den Faktor 2 (Verstärker) am Ausgang anliegt.
R1
Die eigentliche Verstärkung V' des Operationsverstärkers, welche im Bereich 100dB bis 120dB liegt (das
entspricht 100.000 bzw. 1.000.000), fällt aus der Betrachtung vollkommen heraus. Das liegt daran, dass
der Operationsverstärker mit dieser Beschaltung ein rückgekoppeltes System ist.
Stellt man Gleichung I) nach dem Strom um, so erhält man: i1 =
uE
–
uE '
V'
k ⋅uA
k
uA '
uA
uA
Die Ausgangsspannung wird mit dem Faktor k wieder an den Eingang des Verstärkers geführt. Dieser
verstärkt daraufhin die Spannung u E ' , welche sich wie folgt zusammen setzt: u E ' = u E − k ⋅ u A . Die
Spannung u A * am Ausgang des Verstärkers ist: u A ' = V'⋅u E ' . Sie entspricht der Spannung u A . Damit
kann man allgemein schreiben:
u A = u A ' = V'⋅u E ' = V'⋅(u E − k ⋅ u A )
⇔ u A = V'⋅u E − k ⋅ V'⋅u A
⇔ u A + k ⋅ V'⋅u A = V'⋅u E
⇔ u A ⋅ (1 + k ⋅ V') = V'⋅u E
⇔
uA
V'
=V=
uE
1 + k ⋅ V'
uA
1
=V=
.
1
uE
+k
V'
In der Elektrotechnik ist eine Verstärkung von 100dB bis 120dB (hier also für V' ) nahezu Unendlich.
⎛ 1 ⎞ 1
⎟ = . Die allgemeine
Dadurch ergibt sich folgende Grenzwertbetrachtung: lim V = lim ⎜⎜ 1
⎟
V'→∞
V'→∞
⎝ V' + k ⎠ k
Verstärkung V ist also vollkommen unabhängig vom Operationsverstärker ( V' ), sie hängt lediglich vom
Kopplungsfaktor k ab.
Dividiert man Zähler und Nenner durch V' , so erhält man den Ausdruck:
University of Applied
Sciences Cologne
Operationsverstärker
Tutorium
Differenzierer
OP-03
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Die Vorgehensweise bei der Bestimmung, ob es sich um einen Integrierer oder Differenzierer handelt, ist
die gleiche wie beim invertierenden Verstärker. Lediglich der allgemeine Zusammenhang bei der
Induktivität und Kapazität zwischen Spannung und Strom müssen bekannt sein (siehe Grundlagen).
L
iL
iC
uL
uL = L⋅
C
uC
di L
dt
uC =
1
⋅ i C dt
C ∫
Setzt man zum Beispiel eine Spule an die Stelle von R 2 ein und legt die Maschen wie gehabt an, so
erhält man folgende Zusammenhänge:
L
i1
iD
R
i2
uD
uE
uA
I)
II)
− i 1 ⋅ R + u E = 0 ⇔ u E = i1 ⋅ R
di
di
Masche II) + L ⋅ 2 − u A = 0 ⇔ u A = L ⋅ 2
dt
dt
Knotengleichung: + i1 + i 2 − i D = 0 ⇔ i 2 = −i1
Masche I)
Masche I) wird nach dem Strom umgestellt und in Masche II) eingesetzt:
uE
R
di
d (− i1 )
d⎛ u ⎞
L d uE
= L⋅ ⎜− E ⎟ = − ⋅
uA = L⋅ 2 = L⋅
dt
dt
dt ⎝ R ⎠
R dt
{
τ
u E = i1 ⋅ R ⇔ i1 =
L d uE
⋅
. Die Ausgangsspannung ist eine Funktion der Eingangsspannung, sie
R dt
d
entspricht der ersten Ableitung . Der Operationsverstärker arbeitet als Differenzierer.
dt
Es ist u A = f (u E ) = −
University of Applied
Sciences Cologne
Operationsverstärker
Tutorium
Integrierer
OP-04
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Tauscht man die Spule gegen einen Kondensator aus, so erhält man einen Integrierer. Da ganze kann man
mit Hilfe der Maschen am Eingang und Ausgang sowie der Knotengleichung beweisen.
C
i1
iD
R
i2
uD
uE
uA
I)
II)
− i 1 ⋅ R + u E = 0 ⇔ u E = i1 ⋅ R
1
1
Masche II) + ⋅ ∫ i 2 dt − u A = 0 ⇔ u A = ⋅ ∫ i 2 dt
C
C
Knotengleichung: + i1 + i 2 − i D = 0 ⇔ i 2 = −i1
Masche I)
Einsetzen des Stroms aus Masche I) in Masche II):
u E = i1 ⋅ R ⇔ i1 =
uA =
uE
R
1
1
1 ⎛ u ⎞
1
⋅ ∫ i 2 dt = ⋅ ∫ (− i1 )dt = ⋅ ∫ ⎜ − E ⎟dt = −
⋅ u E dt
C
C
C ⎝ R⎠
R ⋅C ∫
{
1
τ
1
⋅ u E dt . Die Ausgangsspannung ist eine Funktion der Eingangsspannung, sie
R ⋅C ∫
entspricht der Fläche (Integral) ∫ dt . Der Operationsverstärker arbeitet als Integrierer.
Es ist u A = f (u E ) = −
University of Applied
Sciences Cologne
Operationsverstärker
Tutorium
Differenzierer / Integrierer
Ü-OP-01
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Aufgabe 1:
Bestimme die Funktion der abgebildeten Operationsschaltung.
a)
R
L
uE
uA
b)
R
C
uE
uA