Seminar 3

Ergänzende Materialien zur Vorlesung
Theoretische Mechanik, WS 2005/06
Dörte Hansen
Seminar 3
1 Dissipative Kräfte I – Reibung
Wenn wir in der theoretischen Mechanik die Bewegung eines Körpers beschreiben wollen,
müssen wir in der Regel verschiedene Modellannahmen treffen. So z.B. vernachlässigt
das Modell Massenpunkt“ die inneren Freiheitsgrade eines ausgedehnten Körpers. Eine
”
weitere, weit verbreitete Annahme betrifft die Frage nach der Energieerhaltung innerhalb
des betrachteten Systems. Genau genommen, gibt es keine abgeschlossenen Systeme und
damit auch keine Energieerhaltung 1 . Durch Wechselwirkungen mit der Welt außerhalb
des von uns betrachteten Systems, mit den Teilchen der Luft oder - in der Himmelsmechanik - mit dem interstellaren Medium wird unserem System Energie zugeführt oder
aber Energie von unserem mechanischen System abgezogen. Im folgenden wollen wir uns
insbesondere einem dieser dissipativen Prozesse zuwenden: der Reibung.
1.1 Reibung eines Körpers in Gasen und Flüssigkeiten
Bei seiner Bewegung durch Gase oder Flüssigkeiten stößt“ ein Körper ständig mit den
”
Teilchen des Gases bzw. der Flüssigkeiten zusammen. Dabei wird ein Teil der Bewegungsenergie des Körpers auf die Gasteilchen übertragen, anders ausgedrückt, es findet
eine Umwandlung der mechanischen Energie des Körpers in thermische Energie der
Gasteilchen statt. Dieser Vorgang kann durch eine dissipative Kraft, die sogenannte
Reibungskraft FR , beschrieben werden. Es ist leicht einsehbar, dass die Reibungskraft
von der Geschwindigkeit v des Körpers abhängig sein sollte. Eine exakte mathematische
Modellierung dieser Kraft ist äußerst schwierig. Empirisch zeigt sich jedoch, dass die Geschwindigkeitsabhängigkeit der Reibungskraft häufig durch ein Potenzgesetz beschrieben
werden kann. So wird in der Regel der Ansatz
FR = −βv n
1
v
v
Außer unserem Universum als Ganzes betrachtet, und auch da ist man sich nicht ganz sicher.
1
verwendet. Zu diesem allgemeinen Ansatz wollen wir später zurückkehren, doch zunächst
wollen wir zwei Spezialfälle gesondert betrachten. Für die praktische Anwendung sind
insbesondere die Fälle n = 1 und n = 2 von großer Bedeutung. Die durch n = 1
charakterisierte Stokessche Reibung
FR = −βv
ist linear von der Geschwindigkeit abhängig. Sie findet ihre Anwendung vor allem in
der schnellen Ballistik (d.h. bei der Beschreibung der Bewegung schneller Geschosse)
oder bei der langsamen Bewegung eines Körpers in zähen Flüssigkeiten. Die Newtonsche
Reibung wiederum wird durch ein quadratisches Reibungsgesetz
FR = −βv v
charakterisiert und findet vor allem in der langsamen Ballistik ihre Anwendung. Nat ürlich
gibt es nicht eine universelle Grenzgeschwindigkeit für die Bewegung in Gasen, unterhalb
derer das Newtonsche Reibungsgesetz zur Geltung kommt. Man kann zwar in der Tat
eine solche Grenzgeschwindigkeit v g angeben, aber diese hängt von der Viskosität des
Substrats ab. Das Stokessche Reibungsgesetz wird man immer dann anwenden, wenn die
Geschwindigkeit des betrachteten Körpers im Medium oberhalb dieser Grenzgeschwindigkeit liegt.
1.1.1 Der schräge Wurf mit Stokesscher Reibung
Als Beispiel für die Bewegung eines Massenpunktes unter dem Einfluss Stokesscher Reibung betrachten wir den wohlbekannten schrägen Wurf (siehe Skizze). Mit der Reibungskraft
FR = −β ṙ
lautet die Bewegungsgleichung des Massenpunktes
mr̈ = −β ṙ − mge3 .
(1)
Der schräge Wurf ist eine ebene Bewegung, daher können wir ohne Beschränkung der Allgemeinheit annehmen, dass sich der Massenpunkt nur in der xz-Ebene bewegt. Schreiben
wir Gl. (1) als eine Differentialgleichung 1. Ordnung in v,
β
dv
= −g
v + e3 ,
(2)
v̇ =
dt
mg
so könnten wir nun natürlich versuchen, diese Gleichung durch Separation der Variablen
zu integrieren. Es bietet sich hier jedoch an, einen einfachen Trick zu verwenden. Multiβ
pliziert man beide Seiten der Gl. (2) mit e m t , und bringt alle geschwindigkeitsabhängigen
Terme auf die linke Seite, so ergibt sich
β
β
dv
β
+ v e m t = −ge3 e m t .
(3)
dt
m
|
{z
}
„
«
d
dt
β
v emt
2
Wir können also sofort integrieren und finden
β
v emt = −
β
mg
e3 e m t + c 0 .
β
(4)
Die Konstante c0 bestimmen wir mit Hilfe der Anfangsbedingung v(0) = v 0 . Setzen wir
in Gl. (4) t = 0, so ist
v0 = −
mg
e3 + c 0 ,
β
woraus wir c0 sofort ablesen können. Damit erhalten wir für die Geschwindigkeit
β
β
mg e3 1 − e − m t + v 0 e− m t .
v(t) = −
β
Die Integration dieser Gleichung ist nun trivial und führt uns auf
β
mg
m
m −βt
m
r(t) = c1 −
e3 t + e
− v0 e− m t .
β
β
β
(5)
(6)
Die Konstante c1 ist durch die Anfangsbedingungen festgelegt. Setzen wir in Gl. (6)
t = 0, so ergibt sich
r0 = c 1 −
m2 g
m
e3 − v0
2
β
β
=⇒
c 1 = r0 +
m2 g
m
e3 + v0 .
2
β
β
Die Weltlinie unseres Massenpunktes ist also durch
m2 g mg β
β
m −m
−m
t
t
+
−
1−e
t e3
r(t) = r0 + v0 1 − e
β
β2
β
gegeben. Komponentenweise erhalten wir
β
mv0
x(t) =
cos α 1 − e− m t ,
β
β
mv0
mg
m2 g 1 − e− m t .
z(t) = z0 −
t+
sin α + 2
β
β
β
(7)
(8)
(9)
(10)
Auf den ersten Blick sind kaum Gemeinsamkeiten mit der uns vertrauten Darstellung der
β
in der Regel sehr
ohne Reibung berechneten Wurfparabel zu erkennen. Nun ist aber m
β
klein. Wir wollen uns deshalb überlegen, wie die Lösungen (9) für m t 1 näherungsweise
aussehen. Dazu entwickeln wir die Exponentialfunktion in eine Taylorreihe
3 β
β 3
β
1 β2 2
t
−m
=1− t+
t +O
t
e
(11)
m
2 m2
m3
und setzen diese Entwicklung in Gl. (9) ein. Zu beachten ist hierbei, dass wir auch die
quadratischen Terme in der Entwicklung der Exponentialfunktion mitnehmen müssen
3
20
15
10
5
0
0
10
20
30
40
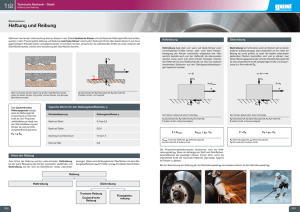
Abbildung 1: Schräger Wurf mit Stokesscher Reibung für verschiedene Reibungskoeffizienten β. Je größer β, desto kürzer ist die Wurfweite. Die gestrichelte Kurve
kennzeichnet die klassische“ Wurfparabel ohne Reibung.
”
um die erste, durch Reibung verursachte Korrektur zur herkömmlichen Wurfparabel zu
erfassen. Wir finden somit
3 mv0
β
β2 2
β 3
x(t) =
1−1+ t−
cos α
(12)
t +O
t
2
β
m
2m
m3
1β
v0 t2 cos α + O β 2 ,
(13)
= v0 t cos α −
2
m
3 mv0
mg
β
m2 g
β2 2
β 3
z(t) =
−
1−1+ t−
t
+
O
t
sin α + 2
t + z0 (14)
β
β
m
2m2
m3
β
1 βv0 2
g
t sin α + O β 2 .
(15)
= − t2 + v0 t sin α + z0 −
2
2 m
Wir sehen also, dass die erste nichtverschwindende Korrektur zur klassischen“ Wurf”
parabel linear in β und proportional zu t 2 ist. In der Tat liefert (12) eine sehr gute
β
ist klein gegen Eins.
Näherungslösung für nicht zu große Zeiten t - vorausgesetzt, m
1.1.2 Freier Fall mit Newtonscher Reibung
Das Newtonsche Reibungsgesetz
FR = −βv v,
β>0
wird angewendet, so lange die Geschwindigkeit des sich bewegenden Körpers nicht eine
von der Viskosität des Mediums abhängige Grenzgeschwindigkeit überschreitet (langsame Ballistik). Wir wollen uns im Folgenden auf die eindimensionale Bewegung eines
4
Massenpunktes im homogenen Schwerefeld der Erde beschränken2 . Die Bewegungsgleichung des Massenpunktes lautet
β
ẋ|ẋ| .
(16)
ẍ = −g − β ẋ|ẋ| = −g 1 +
mg
Schauen wir uns Gl. (16) etwas geneuer an: Offenbar ist ẋ nur dann positiv, wenn der
Massenpunkt sich entgegen der Erdanziehungskraft bewegt, also mit anderen Worten,
beim senkrechten Wurf nach oben. Selbst in diesem Fall wird die Bewegung des Massenpunktes aber endlicher Zeit umkehren, so dass nach dem Umkehrpunkt auch hier ẋ < 0
gilt. Unabhängig von den Anfangsbedingungen ẋ(0) = v 0 wird daher für große Zeiten
immer
β 2
ẋ
ẍ = −g 1 −
(17)
mg
gelten. In dem (in der Praxis natürlich unrealistischen) Limes t → ∞ sollten sich Erdanziehungskraft und Reibungskraft gerade kompensieren,
d.h. der Massenpunkt sollte sich
q
bewegen.
In Abhängigkeit von den
mit konstanter Endgeschwindigkeit −v ∞ = − mg
β
Anfangsbedingungen unterscheiden wir:
• v0 > 0
Das entspricht dem senkrechten Wurf nach oben. Die Aufwärtsbewegung des Massenpunktes wird aber nach endlicher Zeit t u zum Stillstand kommen; anschließend
setzt der freie Fall des Massenpunktes ein. Den ersten Teil der Bewegung beschreibt
die Bewegungsgleichung
v2
β 2
v = −g 1 + 2 .
v̇ = −g 1 +
mg
v∞
Separation der Variablen und anschliessende Integration führt auf
Z v
v0
dv
v
v v
− arctan
−gt =
= v∞ arctan
,
= v∞ arctan
v2
v ∞ v0
v∞
v∞
v0 1 + v 2
v>0
∞
Im Umkehrpunkt der Bewegung ist v = 0 und wir erhalten
−gtu = − arctan
v0
,
v∞
so dass
−g(t − tu ) = v∞ arctan
2
v
v∞
=⇒
v(t) = −v∞ tan
g
(t − tu ),
v∞
t ≤ tu .
Man kann sich leicht überlegen, dass selbst die in 50 Kilometern Höhe über der Erdoberfläche wirksame
Schwerebeschleunigung nur wenig von dem auf der Erdoberfläche gültigen Wert abweicht. Zumindest
in den unteren 50 Kilometern der Erdatmosphäre kann also g näherungsweise als konstant engesehen
werden.
5
Bei t = tu beginnt der freie Fall des Körpers, wobei die Geschwindigkeit v = −v ∞
erst nach unendlich langer Zeit erreicht werden würde. Die Bewegungsgleichung
v2
v̇ = −g 1 − 2
v∞
(beachte: v < 0) hat nun die Lösung 3
Z
Z t
dt = −g(tu − t) =
−g
tu
v
0
dv
1−
v2
2
v∞
= v∞ artanh
v
v∞
bzw.
v = −v∞ tanh
g
(t − tu ),
v∞
t ≥ tu .
Insgesamt erhalten wir somit
v = −v∞
tan vg∞ (t − tu ) t ≤ tu
tanh vg∞ (t − tu ) t > tu
• −v∞ < v0 < 0:
Dieser Fall ist im Prinzip schon behandelt worden. Die Bewegungsgleichung
v2
(18)
v̇ = −g 1 − 2
v∞
führt auf
v
v0
−gt = v∞ artanh
− artanh
v∞
v∞
• v < −v∞ < 0
Betrachten wir zum Schluss Situationen, in denen die Anfangsgeschwindigkeit betragsmäßig größer als v∞ . Wie oben bereits gesagt, nähert sich die Geschwindigkeit
des Massenpunktes asymptotisch jenem Wert −v ∞ an, ohne ihn in endlicher Zeit
zu erreichen. Wenn |v| also zur Zeit t = 0 grp̈ßer ist als v ∞ , so wird die Geschwindigkeit des Massenpunktes für alle Zeiten größer sein als v∞ . Wir müssen nun den
anderen Lösungsast der Bewegungsgleichung (18) wählen, also
v0
v
− arcoth
−gt = v∞ arcoth
.
v∞
v∞
3
Es gilt:
Z
dv
2 =
1 − vv2

v∞ artanh vv∞
v∞ arcoth vv∞
∞
6
−v∞ < v < 0
v < −v∞ < 0
Derartige Anfangsbedingungen gelten z.B. für den Fall eines Meteoriten im Schwerefeld der Erde. Er trifft mit sehr hoher Geschwindigkeit auf die Erdatmosphäre
und wird während seiner Reise durch verschiedenen Schichten der Atmosphäre
stark abgebremst. Verdampft er nicht vorher aufgrund der dabei entstehenden
Reibungshitze vollständig so wird seine Geschwindigkeit selbst beim Aufprall auf
die Erdoberfläche noch wesentlich höher sein als v∞ .
7