1 Elektrostatik
Werbung

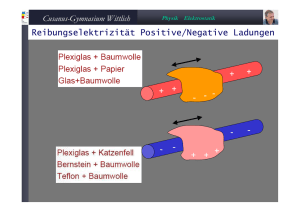
1 Elektrostatik 1.1 Ladung 1.1.1 Eigenschaften Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 1 Das heutige Bild vom Aufbau eines Atoms Größe < 10-18m Größe ≈ 10-14m Größe < 10-18m Größe ≈ 10-15m Größe ≈ 10-10m Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 2 Ausblick: Ladung der Quarks & Hadronen Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 3 Reibungselektrizität Altgriechisch: ἤλεκτρον = Bernstein Versuch: „Erzeugung“ von elektrischer Ladung durch Reibung (Genauer: Die Reibung trennt positive und negative Ladungen) 1. Fell und Hartgummistab Elektronen fließen vom Fell auf den Kunststoffstab. Kunststoffstab ist negativ geladen. - 2. Seidentuch und Glasstab Elektronen fließen vom Glasstab auf das Seidentuch. Glastab ist positiv geladen. - - - + Abstoßung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Anziehung Kapitel 1: Elektrostatik / 4 Versuch: Van de Graaff Generator Vorrichtung die durch Reibung positive und negative Ladungen trennt. Eine Elektrode wird stark aufgeladen. http://libraries.mit.edu/archives/exhibits/van-de-graaff/ Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 5 Van de Graaff Generator am Hahn-Meitner Institut (Berlin), erzeugt 5 MV (Spannungen > 2MV nur mit Isoliergas, z.B. SF6 mit 1MPa) Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 6 Verbreiteter Typ von Teilchenbeschleunigern: Tandem-van-de-Graaff-Beschleuniger Meier Leibnitz Labor München MPI Heidelberg Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 7 1.1.2 Das Coulomb Gesetz: Kraft zwischen zwei Punktladungen Charles A. de Coulomb (1736 – 1806) Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 8 Beispiel: Größenvergleich Coulombkraft - Gravitationskraft Was hält dann die Protonen im Kern zusammen? Starke Kernkraft Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 9 Überlagerung (Superposition von Kräften) a) Diskrete Verteilung von Ladungen b) Kontinuierliche Ladungsverteilung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 10 Wiederholung q Coulombkraft zwischen 2 Punktladungen r FC = qQ r ⋅ 2 ⋅ er 4πε 0 r Q r qQ r = ⋅ 3 ⋅r 4πε 0 r 1 1 Nm 2 f = ≈ 9 × 10 4πε 0 C2 1 9 Kraft zwischen Ladung q und Raumladungsverteilung ρ(r) : q R-r r R Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 () r r F R = q 4πε 0 V∫ ( ) r r r R−r r r 3 ρ (r )dV R−r Kapitel 1: Elektrostatik / 11 1.2 Das Elektrische Feld 1.2.1 Die elektrische Feldstärke Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 12 1.2.2 Bestimmung der Elementarladung: Millikan-Versuch Robert A. Millikan (1868 – 1953) Nobelpreis 1923 Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 13 1.2.3 Leiter im elektrischen Feld - Influenz Leiter: Isolator: Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 14 Versuch: Influenzmaschine von Wimshurst Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 15 1.2.4 Feldlinien des elektrischen Feldes Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 16 Versuch: Ausrichtung von Grieskörnern (ungefähe) entlang der Feldlinien ++ + -- + - - Die Grieskörner schwimmen in Rhizinusöl. Weil sie im Feld kleine Dipole werden, richten sie sich entlang der Feldlinien aus (Die Spannung zwischen + und – beträgt hier 10000V). + - Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 + - Kapitel 1: Elektrostatik / 17 Elektrisches Feld zweier Punktladungen Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 18 1.2.5 Das Superpositionsprinzip für elektrische Felder Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 19 Beispiel: Elektrisches Feld eines gleichmäßig geladenen, dünnen Stabes Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 20 Spezialfälle Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 21 1.2.6 Elektrischer Dipol im elektrischen Feld Van der Waals Kräfte Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 22 1.2.7 Der elektrische Fluss, Gaußscher Satz Um was geht es? Zusammenhang zwischen dem “elektrischen Kraftfluss” durch eine geschlossene Fläche und der eingeschlossenen Ladung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 23 Carl Friedrich Gauß (1777-1855) Der elektrische Fluss durch eine geschlossene Oberfläche, hängt weder von der Form der Oberfl., noch von der Ladungsverteilung ρ(r) ab, sondern nur von der eingeschlossenen Ladung Q. Die im Raum verteilten Ladungen sind die Quellen (ρ(r) > 0) bzw. die Senken (ρ(r) < 0) des elektrischen Feldes. Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 24 Beispiele zum Gaußschen Gesetz (I): Feld einer Punktladung Ladung auf beliebig geformten Leitern Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 25 Beispiele zum Gaußschen Gesetz (II): Feld einer leitenden Kugel (Ladung Q) Feld einer homogen geladenen Kugel (Isolator, Ladung Q) Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 26 Beispiele zum Gaußschen Gesetz (III): Feld eines unendlich langen, homogen geladenen, dünnen Stabes Feld eines unendlich langen, homogen geladenen, leitenden Zylinders Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 27 Beispiele zum Gaußschen Gesetz (IV): Feld einer homogen geladenen, unendlichen Ebene Feld eines Plattenkondensators Feld in der Nähe der geladenen Oberfläche eines Leiters Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 28 Versuch: a) Feldlinien im Plattenkondensator b) Faraday Käfig Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 29 Wiederholung: Elektrisches Feld verschiedener symmetrischer Ladungsverteilungen (elegante Berechnung mit Gaußschem Satz) 1 E= Ladung q auf der Oberfläche einer leitenden Kugel mit Radius R q ⎧ 1 ⋅ 2 r>R ⎪ E = ⎨ 4πε 0 r ⎪⎩ 0 r<R Ladung Q, homogen verteilt in nichtleitender Vollkugel mit Radius R Unendlich langer Draht mit linearer Ladungsdichte λ Unendlich langer, leitender Zylinder mit Radius R, linearer Ladungsdichte λ Eine unendliche, geladene Ebene mit Flächenladungsdichte σ Feld zwischen zwei entgegengesetzt geladenen, unendlichen Ebenen mit Flächenladungsdichte σ (Plattenkondensator) Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 4πε 0 ⋅ q r2 Punktladung q ⎧ 1 ⎪⎪ 4πε 0 E=⎨ 1 ⎪ ⎪⎩ 4πε 0 E= 1 ⋅ Q r2 Q ⋅r R3 ⋅ r>R r<R λ 2πε 0 r ⎧ 1 λ ⋅ r>R ⎪ E = ⎨ 2πε 0 r ⎪⎩ 0 r < R σ E= 2ε 0 σ E= ε0 Kapitel 1: Elektrostatik / 30 1.3 Das elektrische Potenzial & elektrische Spannung 1.3.1 Arbeit und potenzielle Energie im elektrischen Feld (Halliday / Resnick) 2 Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 31 Beispiel: Potenzielle Energie von mehreren Punktladungen Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 32 1.3.2 Elektrisches Potenzial und Spannung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 33 Äquipotenziallinien und Feldlinien Aquipotentiallinie = Kurve die Punkte mit gleichem Potenzial verbindet Feldlinien stehen immer senkrecht auf den Äquipotanziallinien (da E = - grad φ) Gravitationsfeld: Äquipotenziallinien = Höhenlinien Feldlinien = Linien des “steilsten Anstiegs” Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 34 Beispiel: Potenzial im homogenen elektrischen Feld Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 35 Beispiel: Beschleunigung von Ionen und Elementarteilchen (z.B. mit Tandem Van-de-Graaf Beschleuniger) MV Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 36 Beispiel: typische Teilchenenergien Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 37 1.3.3 Berechnung des Potenzials Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 38 Beispiel: Potenzial auf der Achse eines dünnen Ringes Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 39 Potenzial einer geladenen, leitenden Kugel Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Potenzial einer geladenen, nichtleitenden Kugel Kapitel 1: Elektrostatik / 40 1.3.2 Poisson- und Laplace-Gleichung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 41 Wiederholung: Elektrisches Potenzial verschiedener Ladungsverteilungen 1 Q r Punktladung Q ϕ (r) = Ladung Q auf der Oberfläche einer leitenden Kugel mit Radius R (oder leitende Hohlkugel) ⎧ ⎪⎪ ϕ (r) = ⎨ 1 ⎪ ⎪⎩ 4πε 0 Ladung Q, homogen verteilt in nichtleitender Vollkugel mit Radius R Unendlich langer Draht mit linearer Ladungsdichte λ Feldstärke und Spannung im Plattenkondensator (Plattenabstand d) Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 4πε 0 ⋅ 1 ⋅ Q r r>R 4πε 0 Q ⋅ = konstant R r<R 1 Q ⎧ ⋅ r>R ⎪⎪ 4πε 0 r ϕ (r) = ⎨ ⎛ 3 r2 ⎞ Q 1 ⎪ ⎟ r<R ⋅⎜ − ⎪⎩ 4πε 0 R ⎜⎝ 2 2 R 2 ⎟⎠ ϕ (r) = − E= r λ ⋅ ln , mit ϕ ( R ) = 0. 2πε 0 R U d Kapitel 1: Elektrostatik / 42 Heutiges Thema: Kondensator • • • • • • Was ist ein Kondensator? Wie berechnet man seine Fähigkeit zur Ladungsspeicherung? Wie analysiert man Kondensatoren in einem elektrischen Netzwerk? Wieviel Energie lässt sich in einem Kondensator speichern? Was ist ein Dielektrikum? Warum macht ein Dielektrikum einen Kondensator effizienter? Defibrillator Blitzlicht Kurzer (2 ms) Stromstoß 20A Energie von 200J P = 200J / 2ms = 100kW ! Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 43 1.4 Kondensatoren 1.4.1 Kapazität Neuron Leidener Flasche Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 44 1.4.2 Kapazität eines Plattenkondensators d U Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 45 Plattenkondensator - einige Anwendungen Drehkondensator Kunststofffolienkondensator Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 46 Weitere technische Realisierungen von Kondensatoren Keramikscheibenkondensator Aluminium Elektrolytkondensator Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 MLCC Chipkondensator Tantal Elektrolytkondensator Kapitel 1: Elektrostatik / 47 1.4.3 Kapazität eines Kugelkondensators Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 48 1.4.4 Kondensatoren im Netzwerk (I): Parallel- und Reihenschaltung Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 49 1.5 Energie des elektrischen Feldes Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 50 Beispiele Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 51 Z Machine Sandia Labs: riesige Kondensatorbatterien speichern 106J Energie 1.6 Dielektrika -Q +Q 1.6.1 Dielektrizitätszahl ε ε Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 53 Dielektrizitätszahl einiger Materialien Material ε Vakuum 1 Luft (1atm) 1.00054 3 Polystyrol 2.6 24 Papier 3.5 16 Transformatoröl 4.5 Pyrex 4.7 Glimmer 5.4 Porzellan 6.5 Silizium 12 Germanium 16 Ethanol 25 Wasser (20C) 80.4 Wasser (25C) 78.5 Titania-Keramik 130 Strontiumtitanat 310 Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Durchschlagsfestigkeit (kV/mm) 14 Elektrischer Durchschlag in Glas 8 Kapitel 1: Elektrostatik / 54 Wiederholung: Q C= U Kapazität: +Q -Q Einheit 1 Farad, 1 F = 1 C/V Kapazität eines Plattenkondensators: Fläche A A C = ε0 ⋅ d d U Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 55 Wiederholung: Q C= U Kapazität: +Q -Q Einheit 1 Farad, 1 F = 1 C/V Kapazität eines Plattenkondensators mit Dielektrikum: Fläche A A C = ε 0ε ⋅ d ε Dielektrizitätskonstante ε (Permittivität): d U Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Vakuum Luft Plexiglas Glas Wasser 1 1.00059 3.40 5-10 80 Kapitel 1: Elektrostatik / 56 Was passiert? + + + + + + + + - + + + - + + - + - + - Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 57 1.6.2 Polarisation und dielektrische Suszeptibilität Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 58 Mechanismen der Polarisation • Verschiebungspolarisation • Orientierungspolarisation Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 59 1.6.3 Dielektrische Verschiebungsdichte Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 60 1.6.4 Elektrische Feldenergie im Dielektrikum Caren Hagner / PHYSIK 2 / Wintersemester 2008/2009 Kapitel 1: Elektrostatik / 61