11. Kernzerfälle und Kernspaltung

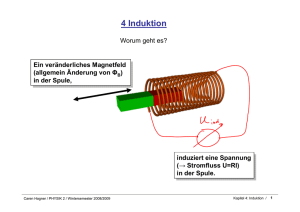
11. Kernzerfälle und Kernspaltung
1.
2.
3.
4.
5.
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Zerfallsgesetz
α – Zerfall
Kernspaltung
ß – Zerfall
γ - Zerfall
Kapitel 11: Kernzerfälle /
1
11.1 Das Zerfallsgesetz
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
2
Zerfallsketten
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
3
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
4
11.2 α-Zerfall
Abspaltung eines 4He Kerns
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
5
Zusammenhang von Eα und λ
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
6
Gamow-Modell des α-Zerfalls (1929)
• klassisch ist α-Zerfall verboten.
• QM: Tunneleffekt
α-Teilchen durchtunnelt die
Coulomb-Barriere.
Wahrscheinlichkeit für α-Zerfall:
λ
wα
vα
Tα
v
  w 
 T
2R
Zerfallskonstante
Präformationswahrscheinlichkeit
Geschwindigkeit des α-Teilchens
Transmissionswahrscheinlichkeit
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
7
Berechnung der Transmission durch die Coulomb-Barriere
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
8
11.3 β-Zerfall
n
u
d
u
u
d
d
p
We
n  p  e  ve
ve
( A, Z)  ( A, Z  1)  e  ve
Gesamte kinetische Energie Q
≈ maximale kinetische Energie des Elektrons
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
9
Kontinuierliches Spektrum der Elektronen aus β- Zerfall → Neutrino! (Pauli 1930)
Man beobachtet drei Arten von β-Zerfällen:
  : n  p  e   e
 :
p  n  e   e
EC : p  e   n  e
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
10
Energiebilanz beim β-Zerfall
1. β- Zerfall ist möglich, falls

 
Be  4e 
11
4
M(A,Z) > M(A, Z+1)
2. β+ Zerfall ist möglich, falls

 
C  6e 
11
6

B  4e  e  e  Q
11
5
M(A,Z) > M(A, Z-1) + 2me

B  6e  e  e  Q
11
5
3. EC / K=Einfang ist möglich, falls M(A,Z) > M(A, Z-1)
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
11
Fermi-Theorie des β-Zerfalls
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
12
Kurie-Darstellung des Elektronspektrums
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
13
Bestimmung der Neutrinomasse im Tritium β-Zerfall: Experiment
von Mainz/Troitsk
3
H  3He  e-   e
E0 = 18.6 keV
dN/dE = K × F(E,Z) × p × Etot × (E0-Ee) × [ (E0-Ee)2 – m2 ]1/2
Mainz Data (1998,1999,2001)
mv2  1.2  2.2  2.1 eV 2
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
 mv  2.2eV 95%CL
Kapitel 11: Kernzerfälle /
14
KATRIN Experiment: Lieferung des Vakuum Tanks des Spektrometers
(Wird gerade in Karlsruhe aufgebaut, Start etwa 2015)
Ziel ist es Neutrinomassen bis 0.2eV/c2 zu messen
(d.h. die aktuelle Grenze von 2eV
um eine Größenordnung zu verbessern)
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
15
11.4 γ-Zerfall
Übergänge zwischen verschiedenen Kernzuständen unter Emission von γ-Strahlung
Elektromagnetische Strahlung
→ Reihenentwicklung als Überlagerung unterschiedlicher Multipolaritäten
(mit den entsprechenden Winkelverteilungen)
Elektrische Dipol-, Quadrupol-, Oktupolstrahlung: E1, E2, E3, …
Magnetische Multipole: M1, M2, M3,…
Erhaltungssätze für Drehimpuls und Parität bestimmen, welche Übergänge möglich:
Für Jf → Ji muss gelten: |Jf - Ji| <
< Jf + Ji
Übergangswahrscheinlichkeit umso größer, je niedriger Multipolarität.
Ml hat gleich große Wahrscheinlichkeit wie E(l+1).
Energieabhängigkeit der Wahrscheinlichkeit:
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
16
γ-Zerfall und innere Konversion
Anregungsenergie des Kerns wird auf Elektron der Atomhülle übertragen
Tritt vor allem dann auf, wenn Abstrahlung eines Photons unterdrückt ist:
• hohe Multipolarität, geringe Energie
• schwerer Kern (größere Aufenthaltswahrscheinlichkeit des Elektrons im Kern)
• Übergänge 0+ → 0+ sind mit Emission eines Photons unmöglich
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
17
Natürliche Zerfallsketten
Name
Typ
Endkern
Startkern
(langlebigster Kern)
T1/2 (Startk.)
in Jahren
Thorium
4n
208Pb
232Th
1.41x1010
Neptunium
4n+1
209Bi
237Np
2.14x106
Uran
4n+2
206Pb
238U
4.47x109
Actinium
4n+3
207Pb
235U
7.04x108
ausgestorben
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
Uran 238 Zerfallsreihe
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
Radonkonzentration in der
Bodenluft (Deutschland)
Quelle: PTB
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
20
11.5 Kernspaltung
Tritt auf bei schweren Kernen, wenn Z2/A > 48.
Man unterscheidet:
• spontane Spaltung
• induzierte Spaltung durch Beschuß mit Teilchen (Neutronen) oder Photonen
Historischer Ablauf:
• 1938: Entdeckung der n-induzierten Spaltung des 238U durch Hahn, Straßmann.
Erste korrekte Interpretation der Experimente durch Meitner und Frisch.
Wenig später: theoretische Beschreibung im Tröpfchenmodell durch
Wheeler und Bohr.
• 1940 Entdeckung der spontanen Spaltung von 238U durch Flerov, Petrzhak.
• 1942 Erste kontrollierte Kettenreaktion durch Fermi in Chicago.
(Isotopenzusammensetzung von natürlichem Uran:
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
0.7% 235U, 99.3% 238U)
Kapitel 11: Kernzerfälle /
21
Otto Hahn
Lise Meitner
Arbeitstisch von O.Hahn
an dem U-Spaltung
entdeckt wurde
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
22
Chicago Pile 1 (CP1), erster “Kernreaktor”, an der Chicago University
E. Fermi
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
23
Energieverhältnisse und Mechanismus der Spaltung
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
24
Induzierte Spaltung
Sehr schwere Kerne (Z ≈ 92): Spaltbarriere nur ca. 6 MeV
Nach Einfangreaktionen von Neutronen entsteht angeregter Kern.
Falls Anregungsenergie > Spaltbarriere → Spaltung des Kerns
Besonders günstig:
Einfang von Neutronen in Kernen mit N = ungerade.
Denn: zusätzlich wird dann die Paarungsenergie frei!
Beispiel: Induzierte Spaltung von 238U und 235U
•
n + 238U → 239U*
dabei wird Bindungsenergie B = 4.8 MeV frei.
Die Spaltbarriere beträgt: Ta = 6.3 MeV. → En > 1.5 MeV für Spaltung.
•
n + 235U → 236U*
dabei wird Bindungsenergie B = 6.4 MeV frei.
Die Spaltbarriere beträgt: Ta = 5.8 MeV.
Schon thermische Neutronen lösen Spaltung aus.
• Auch 233Th, 239Pu eignen sich sehr gut.
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
25
Induzierte Spaltung von 235U
nth  235U 236U *  f1*  f 2*  m  n f  e  Q
• nth
• f1 , f 2
• nf
thermische Neutronen: Ekin ≈ 25 meV.
angeregte Spaltfragmente (neutronenreich), zerfallen weiter durch β-Zerfälle.
schnelle Neutronen: Ekin ≈ einige MeV. Im Mittel m = 2.43
Energiebilanz:
1.
2.
3.
4.
5.
6.
Kinetische Energie der Spaltfragmente _______________
Kinetische Energie der Spaltneutronen _______________
Prompte γ-Strahlung _____________________________
Verzögerte γ-Strahlung aus den Spaltfragmenten _______
β-Strahlung der Spaltfragmente _____________________
Kinetische Energie der Antineutrinos _________________
Maximal absorbierte Energie pro Spaltung: (204 – 12)MeV = 192 MeV = 3·10-11Ws.
Leistung 1 W:
3.25·1010 Spaltungen / s.
1 g Uran:
2.55·1021 Atomkerne, → 22 MWh
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
26
Verteilung der Spaltfragmente
Caren Hagner / PHYSIK 5 / Wintersemester 2013/2014
Kapitel 11: Kernzerfälle /
27