Lösungen zu ¨Ubungsblatt 5 - Arbeitsgruppe Kryptographie und

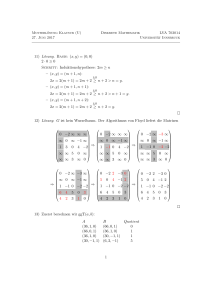
Universität Karlsruhe (TH)
Lösungen zu Übungsblatt 5
Institut für Kryptographie und Sicherheit
Willi Geiselmann (Vorlesung)
Marius Hillenbrand (Übung)
Public Key Kryptographie für Informationswirte
Wintersemester 2009/2010
Übung vom 22. Januar 2010
Aufgabe 1: Wiederholung
Beantworte folgende Fragen. Dabei sind a, b, c, n ∈ N und p eine Primzahl.
(a) Für welche n ist Zn ein Körper?
(b) Für welche dieser n ist Zn zyklisch?
(c) Wie schwer ist es ϕ(n) zu berechnen?
(d) Wie schwer ist es ϕ(n) zu berechnen, wenn die Faktorisierung von n bekannt ist?
(e) Wie schwer ist es n zu faktorisieren?
(f) Wie schwer ist es n zu faktorisieren, wenn ϕ(n) bekannt ist?
(g) Wie schwer ist es zu entscheiden, ob n prim ist?
(h) Wie schwer ist es ggT(a, b) zu berechnen?
Lösung zu Aufgabe 1:
(a) Falls n prim ist (der erweiterte Euklidische Algorithmus garantiert dann die Invertierbarkeit). Ist n nicht prim,
gibt es a, b mit ab = n und mindestens a, b sind nicht invertierbar.
(b) Für alle p ist Z∗p zyklisch. Es gibt ϕ(p − 1) ≥ 1 primitive Elemente, also nicht jedes Element ist primitiv.
(c) Es ist sehr schwer, ϕ(n) zu berechnen, ansosnten wäre das RSA-Verfahren gebrochen (es ließe sich der geheime
Schlüssel d direkt aus dem öffentlichen Schlüssel (e, n) berechnen).
!
r
r
Y
Y
ei
(d) Gegeben der Faktorisierung ist ϕ(n) sehr leicht berechenbar mit ϕ
pi
=
(pei i − pei i −1 ).
i=1
i=1
(e) Die Faktorisierung von n ist sehr schwer, ansonsten wäre ϕ(n) leicht berechenbar und RSA gebrochen.
(f) n kann faktorisiert werden, wenn ϕ(n) bekannt ist (ohne Beweis). Damit ist die Berechnung von ϕ(n) genau so
schwer wie das Faktorisierungsproblem.
(g) Primalität von n kann sehr einfach probabilsitisch z.B. mit dem Rabin-Miller Primzahltest entschieden werden. Es
gibt auch einen deterministischen Primzahltest (den AKS-Test), der in polynomialer Zeit (ohne Fehler) arbeitet.
(h) ggT(a, b) berechnet sich schnell mit den Euklidischen Algorithmus.
Aufgabe 2: Pollard p − 1 Faktorisierungsmethode
Führe den Faktorisierungsalgorithmus von Pollard für die beiden Zahlen 319 (= 11 · 29) und 341 (= 11 · 31) durch.
Weshalb funktioniert er bei der einen Zahl und bei der anderen nicht?
Lösung zu Aufgabe 2:
Iteriere k und berechne für n = 319 und n = 341 jeweils ggT(2k! − 1, n):
k
1
2
3
4
5
6
7
2k! mod 319
2
4
64
49
111
23
1
ggT(2k! − 1, 319)
1
1
1
1
11
11
319
2k! mod 341
2
4
64
16
1
ggT(2k! − 1, 341)
1
1
1
1
341
Im Fall von n = 341 = 11 · 31 unterscheiden sich 11 − 1 = 10 = 2 · 5 und 31 − 1 = 30 = 2 · 3 · 5 nur durch die 3. Dadurch
werden bei der Iteration von k (da k! schnell wächst) gleich alle Faktoren auf einmal erfaßt.
Bei n = 319 = 11 · 29 unterscheiden sich die Faktoren von 11 − 1 = 10 = 2 · 5 und 29 − 1 = 28 = 2 · 2 · 7 um die
Faktoren 2, 5 und 7, weshalb es gelingt, den echten Teiler 11 von 319 abzuspalten.
Aufgabe 3: Faktorisierung mit Dixons Algorithmus und dem quadratischen Sieb
(a) Berechne mit dem Algorithmus von Dixon einen Faktor der Zahl n = 143. Verwende dazu die Zahlen 17, 19 und
34 um Gleichungen aufzustellen, und lege dann eine zu diesen Gleichungen passende Schranke für die Faktorbasis
B fest.
Einige möglicherweise hilfreiche Produkte von Zahlen modulo 143 sind in der folgenden Tabelle gegeben:
172
192
342
17 · 19
17 · 34
17 · 19 · 34
19 · 34
≡
3
≡ 3 · 52
≡ 22 · 3
≡
37
≡
6
≡ 114
≡
74
mod 143
mod 143
mod 143
mod 143
mod 143
mod 143
mod 143
(b) Was sind die wesentlichen Verbesserungen durch das quadratische Sieb?
Lösung zu Aufgabe 3:
(a) Es gilt: Q(17) = 3, Q(19) = 3 · 52 , Q(34) = 22 · 3. In diesen Gleichungen treten nur die Primfaktoren 2, 3 und 5
auf, als Faktorbasis wählen wir daher die Primzahlen ≤ 5.
Diese Gleichungen resultieren in dem Gleichungssystem a · (0, 1, 0) + b · (0, 1, 0) + c · (0, 1, 0) = (0, 0, 0) mit
Koeffizienten in F2 . Eine Lösung ist: a = b = 1, c = 0.
Dies liefert (17·19)2 ≡ 172 ·192 ≡ 3·3·52 ≡ (3·5)2 mod 143. Es ist aber auch bekannt, dass 17·19 ≡ 37 mod 143.
Damit folgt 372 ≡ 152 mod 143. ggT(37 − 15, 143) = ggT(22, 143) = 11 liefert einen echten Teiler.
Eine zweite Lösung ist: a = c = 1, b = 0. Dies liefert (17 · 34)2 ≡ 172 · 342 ≡ 3 · 22 · 3 ≡ (2 · 3)2 mod 143. Damit
folgt 62 ≡ 62 mod 143. ggT(6 − 6, 143) = 143 liefert keinen echten Teiler.
Eine dritte Lösung ist: b = c = 1, a = 0. Dies liefert (19 · 34)2 ≡ 192 · 342 ≡ 3 · 52 · 22 · 3 ≡ (2 · 3 · 5)2 mod 143.
Damit folgt 742 ≡ 302 mod 143. ggT(74 − 30, 143) = ggT(44, 143) = 11 liefert einen echten Teiler.
√
Das ermöglicht es,√dass f (m)
(b)
• Anstatt Q(m) := m2 mod n wird f (m) := (m + b nc)2 − n verwendet.
√
4
leichter über der Faktorbasis B zerfällt. Dazu
wählt
man
1
≤
m
≤
n,
wodurch
f (m) = (m + b nc)2 − n ≈
√
√
√
√
√
4
m2 + 2m n + n − n ≈ n + 2 4 n n ≈ nn2 = n3/4 kleiner ist und leichter über B zerfällt.
• Als Faktorbasis B wird nicht die Menge aller Primzahlen bis zu einer Schranke,sondern
die Menge aller
Primzahlen p kleiner einer Schranke genommen, für die das Legendresymbol np = 1 ist, n also ein
quadratischer Rest modulo p ist.
• Die Zahlen f (m) werden faktorisiert, aber es wird nur die aktuelle Länge blog2 f (m)c gespeichert, was
schneller ist und Platz spart. Wird ein Teiler t von f (m) gefunden, wird die Länge blog2 tc des Teilers
subtrahiert. f (m) zerfällt wahrscheinlich dann, wenn die Länge etwa 0 ist.
• Ist eine Nullstelle m0 des obigen Polynoms modulo p gefunden, sind auch alle m0 + kp (k ∈ N) Nullstellen,
was also eine schnellere Faktorisierung der folgenden f (m) mit größerem m ermöglicht.