nmod ))y(f(fy,nmod)x(fx = = 1)n,yx

4. Übungen zu den Mathematischen Methoden der Kryptologie
SS 2010
19. (Common modulus attack auf RSA) Sind e und d der öffentliche bzw. geheime Schlüssel
für ein RSA-Schema mit dem Modul n bekannt, so kann damit n mit Hilfe des folgenden
RP-Algorithmus in seine Primfaktoren zerlegt werden:
1. Wähle ein zufälliges a ∈ {1,2,.., n − 1} und setze k ← ed-1, sowie t ← ggT(a,n). Ist t>1, so
gib die Primfaktoren t und n/t von n aus, ansonsten mach weiter mit 2.
2. Setze k ← k / 2 und berechne damit den kleinsten Absolutrest b von a k mod n. Ist b ≠ ±1 ,
so gib die Primfaktoren ggT(b ± 1, n ) von n aus, ansonsten setze im Falle, dass b=1 und k
gerade ist mit 2. fort, andernfalls mit 1.
Für welche einstelligen a im angegebenen Bereich würde der obige Algorithmus speziell für
e = 3, d = 7, n = 55 in Schritt 2 zum Erfolg führen? Welche a sind dagegen stets „Nieten“ und
sollten daher in diesem Zusammenhang eigentlich ausgeschlossen werden?
20. Wie müßte man den obigen Algorithmus im Detail umformulieren, wenn man ähnlich wie
beim Miller-Rabin Test von „unten“ kommt, d.h. von einer Darstellung ed-1 = 2 i u mit
ungeradem u ausgeht, damit den kleinsten Absolutrest b von a u mod n bildet und dann die
kleinsten Absolutreste mod n in der Folge b, b 2 , b 4 ,... betrachtet? Man führe ihn konkret für
zwei Werte von a in dem Beispiel aus Aufg. 19 mit unterschiedlichem Ausgang durch.
21. Es sei m>1 eine natürliche Zahl und es werden k natürliche Zahlen zufällig ausgewählt.
Wie groß ist dann die Wahrscheinlichkeit Pk ,m , dass alle k Zahlen in verschiedenen
Restklassen mod m liegen? Was ist speziell für m = 365 das kleinstmögliche k, sodass gilt
Pk ,m < 0.5? (Geburtstagsparadoxon) Welche approximative Formel für Pk ,m würde man man
unter der Voraussetzung k<<m und der dann gültigen Näherung 1-j/m ≈ exp(− j / m) erhalten?
Man versuche damit zu begründen, dass ab k ≈ 1.2 m erstmals Pk ,m < 0.5 sein sollte.
22. Bei der sog. Pollard’schen ρ -Methode zur Faktorisierung einer ganzen Zahl n>1 geht man
so vor, dass für eine einfach gebaute Funktion f(x), deren Werte mod n unter statistischen
Gesichtspunkten „gut streuen“ , zwei Folgen x n und y n , n=0,1,2,…, mit gleichem Startwert
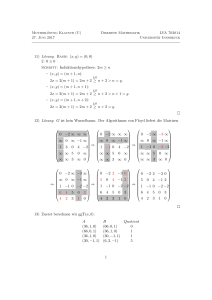
x 0 = y 0 rekursiv definiert durch
x k +1 = f ( x k ) mod n , y k +1 = f (f ( y k )) mod n
und dann für k>0 jeweils überprüft, ob ggT( x k − y k , n ) > 1 ist, womit man dann in der Regel
einen nichtrivialen Teiler von n gefunden hat. Man führe diese Iteration am Beispiel n=6887,
f(x)= x 2 + 1 und x 0 = y 0 = 3 tatsächlich durch.und betrachte dann obige Folgen nochmals,
aber jetzt mod q für den gefunden Faktor q. Warum hat das Verfahren schließlich zum Erfolg
geführt und genau für diese Iteration? Was ist ferner die Anzahl m der verschieden Werte die
f(x) mod q überhaupt annehmen kann und nach etwa wievielen Iterationen durften wir daher
nach Aufgabe 21 einen Erfolg erwarten?
23. Die Pollard’sche p-1-Methode zum Faktorisieren einer natürlichen Zahl n ist dann sehr
erfolgreich, wenn n einen Primfaktor p besitzt, sodass p-1 „potenzglatt“ für eine relativ kleine
Schranke B ist, d.h. wenn für jede Primzahlpotenz q gilt, dass q p − 1 ⇒ q ≤ B . Im Detail geht
sie dann so:
1. Wähle ein zufälliges a ∈ {2,3,.., n − 2} und setze p ← 2 , sowie d ← ggT(a,n). Ist d>1, so ist
mit d bereits ein nichttrivialer Teiler von n gefunden und man ist fertig, andernfalls mache
man wie folgt weiter.
2. Setze q ← p e , wobei e größtmöglich in Hinblick auf q ≤ B für eine vorher festgewählte
Schranke B ist, sowie a ← a q mod n und d ← ggT(a-1,n). Ist d>1, dann STOP und im
(wahrscheinlichen) Falle d<n hat man einen nichtrivialen Teiler von n gefunden.
3. Setze p ← nächstgrößere Primzahl zu p. Ist p>B, dann STOP (Verfahren war Mißerfolg),
ansonsten mach mit 2. weiter.
Man wende diese Methode auf n=667 mit a=2 und B=10 an.
24. Fermat hat seine heute nach ihm benannte Faktorisierungmethode auf n= 2 027 651 281
selbst angewandt. Man führe damit seinen Algorithmus auf folgende Weise durch.
1. Setze u ← ceiling( n ) (=nächstgrößere ganze Zahl zur Wurzel aus n).
2. Ist v =
u 2 − n ganz? Wenn ja, dann ist n=(u+v)(u-v) eine Zerlegung von n, STOP.
3. u ← u+1. Geh zu 2.
Speziell für die Überprüfung der Ganzheit von v im 2.Schritt überlege man sich, wie man das
Newtonsche Näherungsverfahren zur Bestimmung der positiven Nullstelle des Polynoms
x 2 − v = 0 so modifizieren kann, dass man sich nach möglichst wenig Schritten über das
Ergebnis sicher sein kann.